何故やるのか
大学で統計モデリングやベイズ推論を使いそうなので、とりあえずPythonで実装してみる
Pythonでベイズ推論をするライブラリは、PyMC3, Pystan, Edwardなどが存在するらしい
| ライブラリ | 特徴 |
| :---: | :---: | :---: |
| Pystan | Stanという確率的プログラミングを行う言語のPythonラッパー |
| PyMC3 | Python専用のライブラリ、PyMC4ではTensorflowに対応するかも |
| Edward | 2016年に開発が始まったライブラリ、Tensorflow上で動く |
ちなみに、PyMC3は裏でtheanoという最古のディープラーニングのフレームワークが動いていたが、少し前に開発を終了した
今回はPyMC3を使ってベイズ推論を行う
ライブラリの読み込み
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
from tqdm import tqdm
import pymc3 as pm
sns.set_style('darkgrid')
pd.set_option('display.max_columns', None)
pd.set_option('display.max_rows', 500)
plt.rcParams['font.family'] = 'IPAPGothic'
%matplotlib inline
使用するデータ
「Pythonで体験するベイズ推論」という本の冒頭に載っている変化点検出の問題を実装する
本ではPyMC2が使われているが、今回はPyMC3で実装する
あるユーザーが受信した日々のメール数の推移のデータを使用する
# web上からデータをダウンロード
from urllib.request import urlretrieve
urlretrieve('https://git.io/vXTVC', '../input/txtdata.csv')
count_data = np.loadtxt('../input/txtdata.csv')
n_count = len(count_data)
days = np.arange(n_count)
# データを可視化
fig, ax = plt.subplots(figsize=(18, 4))
ax.bar(np.arange(0, n_count, 1), count_data)
plt.show()
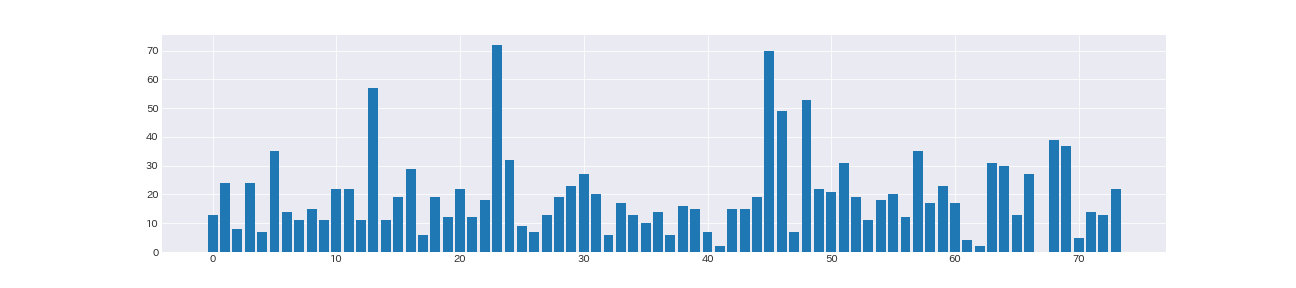
計74日分のデータ
何となく後半の受信メール数が増えているような気がしなくもない
ベイズ推論では、まずこのデータを生成するモデルを考える
モデル生成
変化点を考慮しないモデル
まずは、変化点を考慮しない、日々の受信メール数の平均が常に一定なモデルを組んでみる
$t \in T$日の受信メール数$x_{i}$が、パラメータ$\lambda$のポアソン分布に従うとする
$$
p(x_{i} | \lambda) = Poi(x_{i} | \lambda)
$$
パラメータ$\lambda$は、パラメータ$\alpha$の指数分布に従うとする
$$
p(\lambda | \alpha) = Exp(\lambda | \alpha)
$$
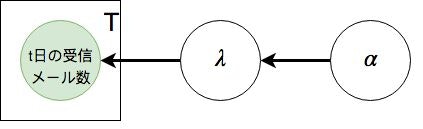
2つの確率分布を組み合わせると、下の図のようになる
$\alpha$によって定められた確率分布から$\lambda$がサンプリングされ、$\lambda$によって定められた確率分布からt日の受信メールがサンプリングされる
*「t日の受信メール数」がTと書かれた四角形で囲われているのは、囲われた四角形の中の値が合計T個存在することを意味する
*「t日の受信メール数」が緑色になっているのは、その変数が観測されている事を意味する
変化点を考慮するモデル
次に、変化点を導入する
上のデータは、実はある日を境に受信メール数が変化していた、とする
変化点の概念をモデルに組み込むためには、t日の受信メール数を生成する確率分布のパラメータ$\lambda$に変更を加える
上のモデルでは$\lambda$は全ての時点で同じだが、変化点の日にちを$\tau$とすると、
\lambda = \left\{ \begin{array}{ll}
\lambda_1 & (t < \tau) \\
\lambda_2 & (t >= \tau)
\end{array} \right.
とすればよい
つまり、変化点の日にちを境に、受信メール数を生成する確率分布のパラメータ$\lambda$が変化する
$\tau$は、最小値$l$、最大値$u$の離散一様分布に従うとする
$$
p(\tau | l, u) = DiscreteUniform(\tau | l, u)
$$
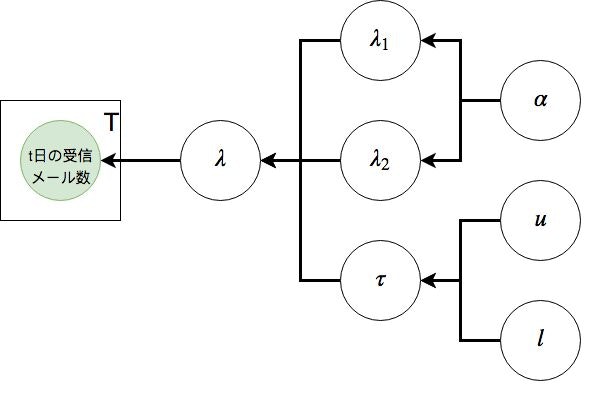
以上を整理すると、下の図のようになる
t日の受信メール数がサンプリングされるまでの流れ
- $\alpha$によって定められた確率分布から$\lambda_1, \lambda_2$がサンプリングされる
- $u, l$によって定められた確率分布から$\tau$がサンプリングされる
- $t < \tau$の時は$\lambda_1$, $t >= \tau$の時は$\lambda_2$となる関数によってt日の$\lambda$が定まる
- $\lambda$によって定められた確率分布からt日の受信メール数がサンプリングされる
PyMC3上では、$\lambda$を求める関数を定数として使うことが出来る(後述)
厳密にいえば$\lambda_1, \lambda_2, \tau$から$\lambda$を返す部分は他の部分と少し違うので、正確な表記の仕方知っている方がいたら教えてくださると嬉しいです
変化点を考慮するモデルの実装
# モデルの構築
basic_model = pm.Model()
with basic_model:
alpha = 1 / count_data.mean()
tau = pm.DiscreteUniform('tau', lower=0, upper=n_count)
lambda_1 = pm.Exponential('lambda_1', alpha) # 指数分布の期待値は1/lambdaとなる
lambda_2 = pm.Exponential('lambda_2', alpha) # lambdaの期待値はデータxの期待値なので、alphaは"1/データxの平均"となる
lambda_ = pm.math.switch(days < tau, lambda_1, lambda_2) # daysがtau未満:lambda_1, tau以上:lambda_2を返す関数、lambda_を定数として扱える
observation = pm.Poisson('observation', lambda_, observed=count_data)
学習
# 学習
# 最初の10000回を捨て、40000回をサンプリング結果として使用する
# chainは2本(デフォルト)
with basic_model:
trace = pm.sample(40000, tune=10000)

# 学習結果
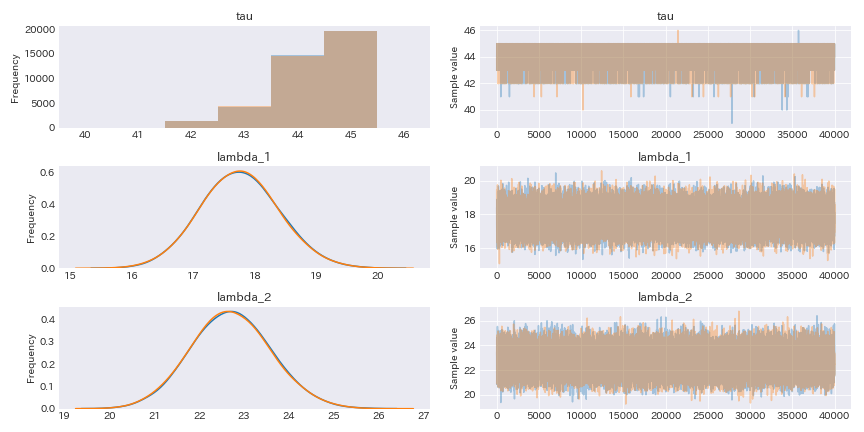
pm.traceplot(trace)
MCMCが収束している事がわかる
パラメータの事後分布について詳細に見ていく
要約統計量
# サンプリング結果の格納
lambda_1_samples = trace.lambda_1
lambda_2_samples = trace.lambda_2
tau_samples = trace.tau
# 要約統計量を求めることもできる
pm.summary(trace)

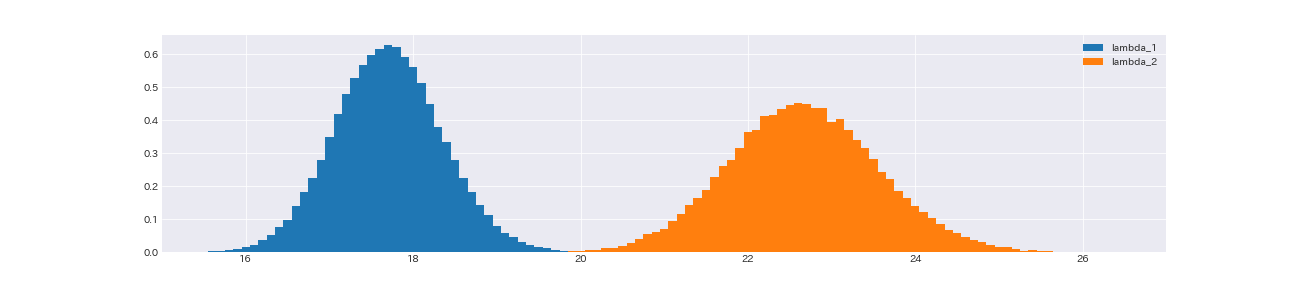
lambda_1, lambda_2
# lambda_1, lambda_2
fig, ax = plt.subplots(figsize=(18, 4))
ax.hist(lambda_1_samples, density=True, bins=np.arange(0, n_count, 0.1), align='left', label='lambda_1')
ax.hist(lambda_2_samples, density=True, bins=np.arange(0, n_count, 0.1), align='left', label = 'lambda_2')
ax.set_xlim(15, 27)
plt.legend()
plt.show()
print('lambda_2がlambda_1より大きい確率:', np.sum(lambda_1_samples < lambda_2_samples) / lambda_1_samples.shape[0])
lambda_2がlambda_1より大きい確率: 1.0
lambda_2の事後分布の方が、lambda_1の事後分布より若干広いものの、全てのサンプリングにおいて、lambda_2はlambda_1より大きい
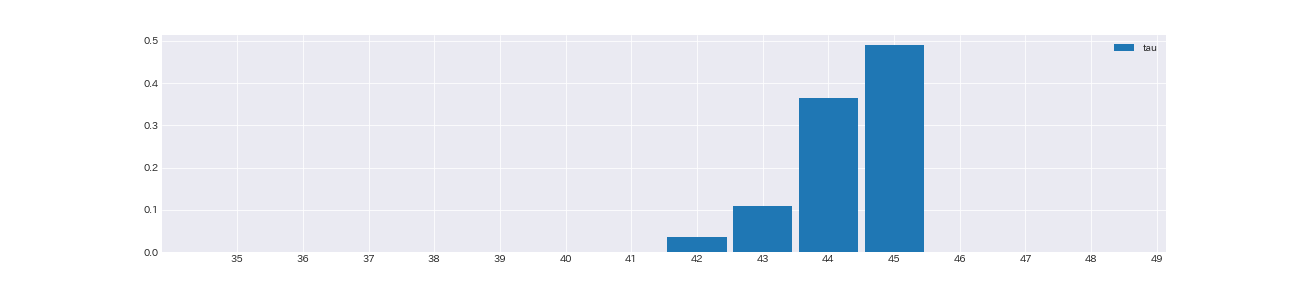
tau
# tau
fig, ax = plt.subplots(figsize=(18, 4))
ax.hist(tau_samples, normed=True, rwidth=0.9, bins=np.arange(35, 50, 1), align='left', label='tau')
ax.set_xticks(np.arange(35, 50, 1))
plt.legend()
plt.show()
変化点は大体45日目である事がわかる
もう少し踏み込んだ分析
# 1日に受け取るメールの期待値を求める
# パラメータlambdaのポアソン分布の期待値はlambdaなので、全てのtauのサンプルを用いてlambdaの期待値を求める
expected_texts_per_day = np.zeros(n_count)
n_tau = tau_samples.shape[0]
for day in range(n_count):
ix = day < tau_samples
expected_texts_per_day[day] = (lambda_1_samples[ix].sum() + lambda_2_samples[~ix].sum()) / n_tau
fig, ax = plt.subplots(figsize=(18, 4))
ax.bar(np.arange(0, n_count, 1), count_data, label='実際のメール受信数')
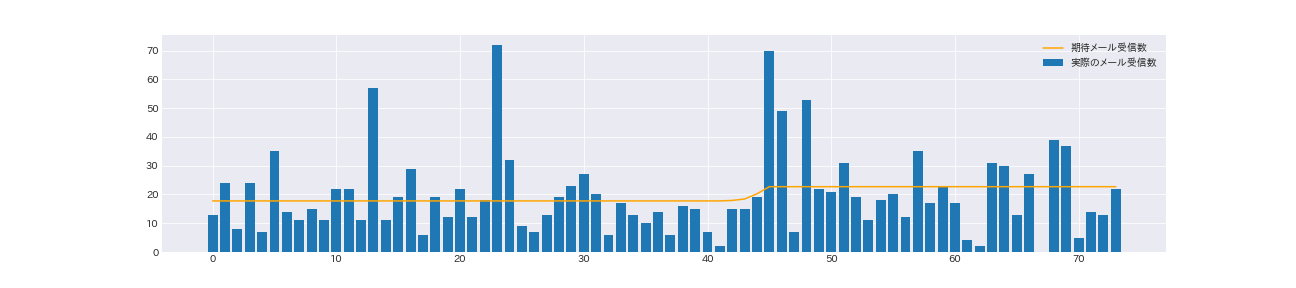
ax.plot(expected_texts_per_day, color='orange', label='期待メール受信数')
plt.legend()
plt.show()
43日目から45日目にかけて、急激に期待受信メール数が増えている事がわかる
期待メール受信数と実際のメール受信数を比べると、突発的にメール受信数が増えているのに引きづられて期待メール受信数が若干高めになっている
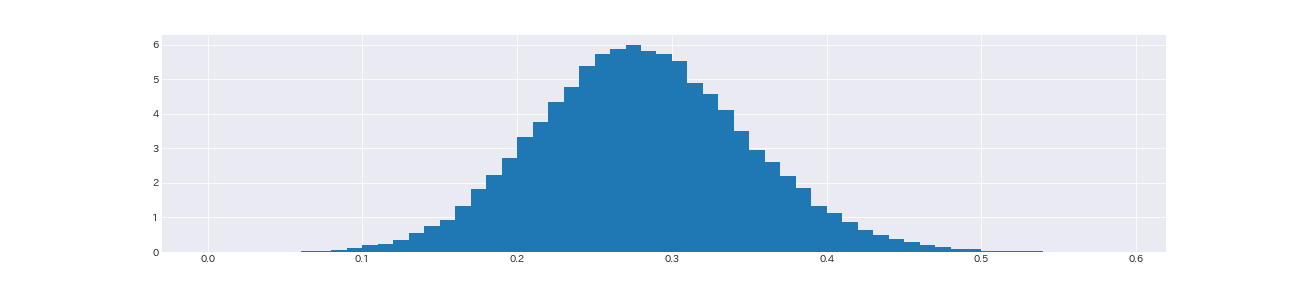
最後に、メール受信数の平均増加率を求める
# メール受信数の期待増加率のヒストグラム
relative_increse_samples = (lambda_2_samples - lambda_1_samples) / lambda_1_samples
fig, ax = plt.subplots(figsize=(18, 4))
ax.hist(relative_increse_samples, bins=np.arange(0, 0.6, 0.01), density=True)
plt.show()
print('受信メール数平均増加率: {:.2f}%'.format(relative_increse_samples.mean() * 100))
受信メール数平均増加率: 28.09%
終わりに
モデル生成から学習、パラメータ等結果の解釈までのやり方を一通りさらった
学習済みモデルを用いれば予測も出来るけど、今回の課題は変化点検出と変化の妥当性の検証なので、予測はまたの機会にします