はじめに
SVMの原理を極力簡単に、見返した時にわかるように記載していく。
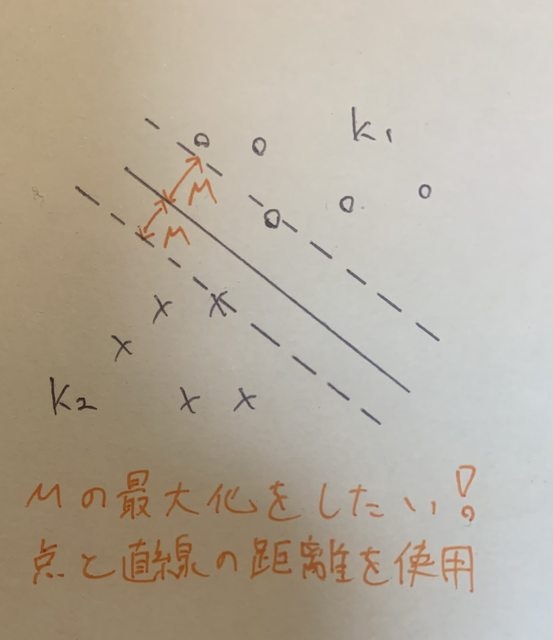
線形分離可能(ハードマージン)
この直線を
$$w^TX_i+b$$
とする。
この時データ群K1, k2において
$$K_1 : w^TX_i+b>0$$
$$K_2 : w^TX_i+b<0$$
が成立する。
負の数を嫌い、ラベル変数$t_i$を導入する
$$K_1 : t_i=1$$
$$K_2 : t_i=-1$$
ラベル変数の導入によって全てのデータで
$$t_i(w^TX_i+b)>0$$
が成立する。
ここでこの直線と各点までの距離は点と直線の距離の計算式により
$$d = \frac{|w_1x_1+w_2x_2+w_3x_3....|}{\sqrt{w_1^2+w_2^2+w_3^2....}}=\frac{|w_i^TX_i+b|}{||w_i||}$$
と書き表せる。
ここでマージンMは上記直線と最寄りの点において
$$M=\frac{w_i^TX_i+b}{||w_i||}=\frac{-(w_i^TX_i+b)}{||w_i||}$$
のどちらかになる。(どちらも正の値なので絶対値は取れる。)
なのでここで求めたいMを最大化する式は
$$maxM : M<=\frac{t_i(w_i^TX_i+b)}{||w_i||}$$
で表すことができる。
ここで両辺をMで割ると
$$1<=\frac{t_i(w_i^TX_i+b)}{M||w_i||}$$
となり、等号が成立し、なおかつ
$$\tilde{w}=\frac{w}{M||w||}$$
$$\tilde{b}=\frac{b}{M||w||}$$
とおくのであれば
$$1=t_i(\tilde{w_i^T}X_i+\tilde{b})$$
が成立する。
この式を
$$maxM : M<=\frac{t_i(w_i^TX_i+b)}{||w_i||}$$に代入すると
$$maxM : M=\frac{1}{||w||}$$が得られる。
最大化問題を最小化問題に変更し、なおかつ唯一解をもつ形に変更すると
$$minM : M=\frac{1}{2}||w||^2$$
が得られる。
過程が違うだけで、やることは線形回帰と同じ。
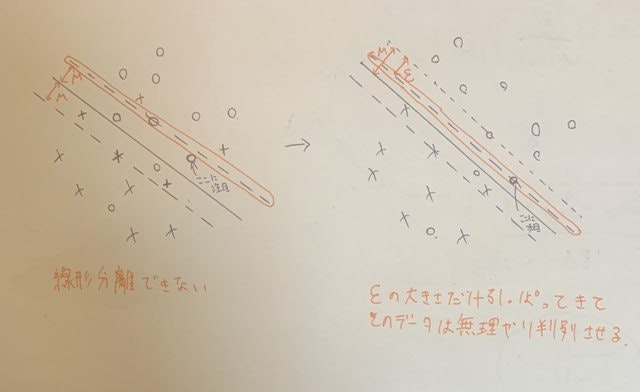
線形分離不可能(ソフトマージン)
判別できるデータは$\epsilon_i$は0となる。(イメージ何もしなくても分別ができるため)
$$t_i(w^T X_i+b)\geq1-\epsilon_i$$
$\epsilon_i$も数が大きいとその回帰直線は分別に向いていないこととなる。
そのため、両者のバランスをとって最適化することが必要となる。
結果最適化式は
$$min(w,\epsilon) : \frac{1}{2}||w||^2 + C\sum_{i=1}^n \epsilon_i$$
となる。
両者のバランスをとりながら最適化していく。
Cはペナルティの大きさ。
ラグランジュ乗数を求める。
難しいのでハードマージンの場合を考える。
ソフトマージンの場合、式に$C\sum_{i=1}^n \epsilon_i$が足されていると考えて問題ない。
今回解きたい式は
$\frac{1}{2}||w||^2$ を $y_{i}(w^{T}x_{i})\geq 1$ という条件の元で最小化する $w$ を求める問題
だと考えるとラグランジュの未定乗数法を使用して双対問題として解くことができる。
また、今回用いるカーネルは線形カーネルを用いる。(計算が簡単なため)
カーネルについては昔の記事に書いたのでそちらを参照ください。
https://qiita.com/hannnari0918/items/c73ca2bc5eee70dc741e
ラグランジュの未定乗数法について詳しくはこちら
この式をラグランジュ関数に置き換える
$$L(w, \lambda) = \frac{1}{2}||w||^2-\sum_{i=1}^n \lambda_i(y_i(w^T x_i)-1)$$
これを解いて求まる解は元式を最小化する。この式を解くと
$$w = \sum_{i_1}^n \lambda_i y_i x_i$$
が求められて代入すると
$$L(\lambda_i) = \sum_{j=1}^n\lambda_i - \sum_{i=1}^n\sum_{j=1}^n\lambda_i \lambda_j y_i y_j k(x_i,x_j)$$
がもとまる。
最急降下法に代入
そもそも上の式がどう出てきてるのか調べてみる。
最急降下法の式としては
$$\theta^{new} = \theta-\alpha\frac{d (目的関数)}{d\theta}$$
$\sum$の中身は求めたい物の微分になる
もともとラグランジュの未定乗数法の求め方としては
$$L(\lambda_i) = \sum_{j=1}^n\lambda_i - \sum_{i=1}^n\sum_{j=1}^n\lambda_i \lambda_j y_i y_j k(x_i,x_j)$$
この式を
$\lambda_i$で微分すると
$$\frac{d L(\lambda_i)}{d\lambda_i} = 1 - \sum_{j=1}^n\lambda_j y_i y_j k(x_i,x_j)$$
の式が得られる。
これを最急降下法の式に代入したものが
$$\lambda_i^{new} = \lambda_i-\alpha(1-\sum_{j=1}^n\lambda_i y_i y_j k(x_i,x_j))$$
になる。
そもそもこの式は
$$L(\lambda_i) = \sum_{j=1}^n\lambda_i - \sum_{i=1}^n\sum_{j=1}^n\lambda_i \lambda_j y_i y_j k(x_i,x_j)$$
$\lambda_i$を求めることでwの最小値が求まる。
ここで$\lambda_i$に対して唯一解を勾配降下法にて求める。
もう少し調べないとだが、最小値ではなく最大値(凸関数なのでどちらでも解ける)を求める。
この問題は$\lambda_i$を最大化する問題に書き換えることができる。(説明は省略) (数学的なトリックらしい...)
そのため、降っていくイメージではなく登っていくイメージに変わるので(最大値を求める式にかわる)
$$\lambda_i^{new} = \lambda_i+\alpha(1-\sum_{j=1}^n\lambda_i y_i y_j k(x_i,x_j))$$
の式を解くことと同義となる。
実際にスクラッチしてみた
import numpy as np
class ScratchSVMClassifier():
"""
SVM分類器のスクラッチ実装
Parameters
----------
num_iter : int
イテレーション数
lr : float
学習率
kernel : str
カーネルの種類。線形カーネル(linear)か多項式カーネル(polly)
threshold : float
サポートベクターを選ぶための閾値
verbose : bool
学習過程を出力する場合はTrue
Attributes
----------
self.n_support_vectors : int
サポートベクターの数
self.index_support_vectors : 次の形のndarray, shape (n_support_vectors,)
サポートベクターのインデックス
self.SV_X_ndarray : 次の形のndarray, shape(n_samples, n_feature)
サポートベクターの特徴量
self.SV_y_ndarray : 次の形のndarray, shape(n_samples, 1)
サポートベクターのラベル
self.SV_ lag_ndarray : 次の形のndarray, shape(n_samples, 1)
サポートベクターのラグランジュ乗数
"""
def __init__(self, num_iter, lr, kernel='linear', threshold=1e-5, verbose=False):
# ハイパーパラメータを属性として記録
self.iter = num_iter
self.lr = lr
self.kernel = kernel
self.threshold = threshold
self.verbose = verbose
# 最大化する関数(勾配降下の逆)
def _gradient_descent(self, X, y, lag):
"""
ラグランジュ関数の最大化を行う
Parameters
----------
X : 次の形のndarray, shape (n_samples, n_features)
訓練データ
y : 次の形のndarray, shape (n_samples, 1)
目的データ
lag : 次の形のndarray, shape(n_samples, 1)
ラグランジュ乗数
lr : float
学習率
Returns
-------
次の形のndarray, shape (n_samples, 1)
更新後のラグランジュ関数
"""
sigma = (lag * y * X).sum(axis=0)
lag = lag + self.lr * (1 - ((y * X) @ sigma).reshape((X.shape[0], 1)))
for i in range(lag.shape[0]):
if lag[i] < 0:
lag[i] = 0
# sigma = 1 * n_features
# y * X = n_sample * n_futures
return lag
def get_SV(self, X, y, lag):
"""
サポートベクターの数及びサポートベクターを取得する
parameters
----------------------
lag : 次の形のndarray, shape(n_samples, 1)
ラグランジュ乗数
C : float
サポートベクターの閾値
returns
----------------------
SV_X_ndarray : 次の形のndarray, shape(n_samples, n_feature)
サポートベクターの特徴量
SV_y_ndarray : 次の形のndarray, shape(n_samples, 1)
サポートベクターのラベル
SV_ lag_ndarray : 次の形のndarray, shape(n_samples, 1)
サポートベクターのラグランジュ乗数
"""
index_list = []
count = 0
# 閾値より高いラグランジュ乗数の個数
count_sv = (lag > self.threshold).sum()
SV_X_ndarray = np.zeros((count_sv, X.shape[1]))
SV_y_ndarray = np.zeros((count_sv, 1))
SV_lag_ndarray = np.zeros((count_sv, 1))
for i in range(lag.shape[0]):
if lag[i] > self.threshold:
# index番号を保存
index_list.append(i)
# 閾値より高いサポートベクターのパラメータを保存
SV_X_ndarray[count] = X[i]
SV_y_ndarray[count] = y[i]
SV_lag_ndarray[count] = lag[i]
count += 1
# 使わないのでインスタンス化
self.n_support_vectors = count_sv
self.index_support_vectors = index_list
return SV_X_ndarray, SV_y_ndarray, SV_lag_ndarray
def fit(self, X, y):
"""
SVM分類器を学習する。検証データが入力された場合はそれに対する精度もイテレーションごとに計算する。
Parameters
----------
X : 次の形のndarray, shape (n_samples, n_features)
訓練データの特徴量
y : 次の形のndarray, shape (n_samples, )
訓練データの正解値
"""
# 初期値の設定
lag = np.zeros((X.shape[0], 1))
lag_history = np.zeros((self.iter, X.shape[0]))
# yの設定
y = y.reshape((y.shape[0], 1))
# 学習
for n in range(self.iter):
lag = self._gradient_descent(X, y, lag)
lag_history[n] = lag.T
# SVの決定
self.SV_X_ndarray, self.SV_y_ndarray, self.SV_lag_ndarray = self.get_SV(X, y, lag)
if self.verbose:
#verboseをTrueにした際は学習過程を出力
print(lag_history)
def predict(self, test_X):
"""
SVM分類器を使いラベルを推定する。
Parameters
----------
X : 次の形のndarray, shape (n_samples, n_features)
サンプル
Returns
-------
次の形のndarray, shape (n_samples, 1)
SVM分類器による推定結果
"""
f = np.zeros((test_X.shape[0], 1))
# テストデータ分推定の実行
for n in range(test_X.shape[0]):
f[n] = (self.SV_y_ndarray * self.SV_lag_ndarray * (self.SV_X_ndarray @ test_X[n:n+1].T)).sum()
if f[n] > 0:
f[n] = 1
else:
f[n] = -1
return f
終わりに
上のコードは問題なく公式のSVCと同等の分類をした。(Irisデータセットでの分類)
# 公式
from sklearn.svm import SVC
svc = SVC(kernel='linear', random_state=0)
svc.fit(X_75, y_75)
svc_pred = svc.predict(X_25)
from sklearn.metrics import classification_report
print(classification_report(y_25, svc_pred))
precision recall f1-score support
-1 1.00 1.00 1.00 63
1 1.00 1.00 1.00 62
accuracy 1.00 125
macro avg 1.00 1.00 1.00 125
weighted avg 1.00 1.00 1.00 125
# 自作
print(classification_report(y_25, my_svc.predict(X_25)))
precision recall f1-score support
-1 1.00 1.00 1.00 63
1 1.00 1.00 1.00 62
accuracy 1.00 125
macro avg 1.00 1.00 1.00 125
weighted avg 1.00 1.00 1.00 125