SVM どこよりもわかるカーネル関数

はじめに

SVMのスクラッチを実装するなかで、カーネルの違いについてしらべた。

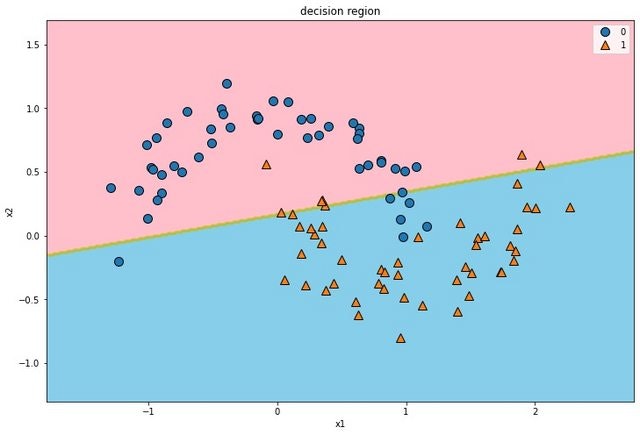
データセット

from sklearn.datasets import make_moons
X, y = make_moons(n_samples=100, noise=0.15)

linear(線形カーネル)

$$k(x_1, x_2) = x_1^T x_2$$

poly_svm = Pipeline([
        ('scaler', StandardScaler()),
        ('svm_clf', SVC(kernel='linear'))
])

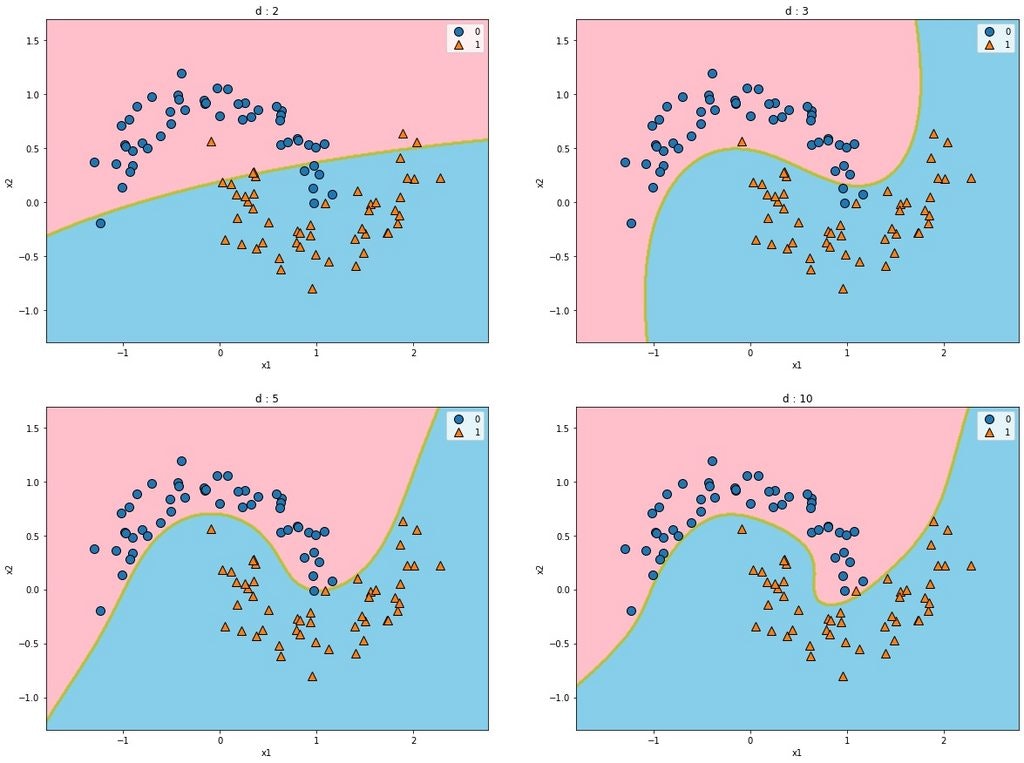
poly(多項式回帰)

線形カーネルとは異なり、特徴量を自分で加えなくともSVCの内部で加えてくれる。
また、カーネルトリックを使用しているため(内積の計算を楽にすること)直接特徴量を加えるより計算速度が断然早くなる。

$$k(x_1, x_2) = (\gamma x_1^T x_2 + r)^d$$

poly_karnel_svm = Pipeline([
    ('sclear', StandardScaler()),
    ('svm', SVC(kernel='poly', degree=3, coef0=1, C=5))
])

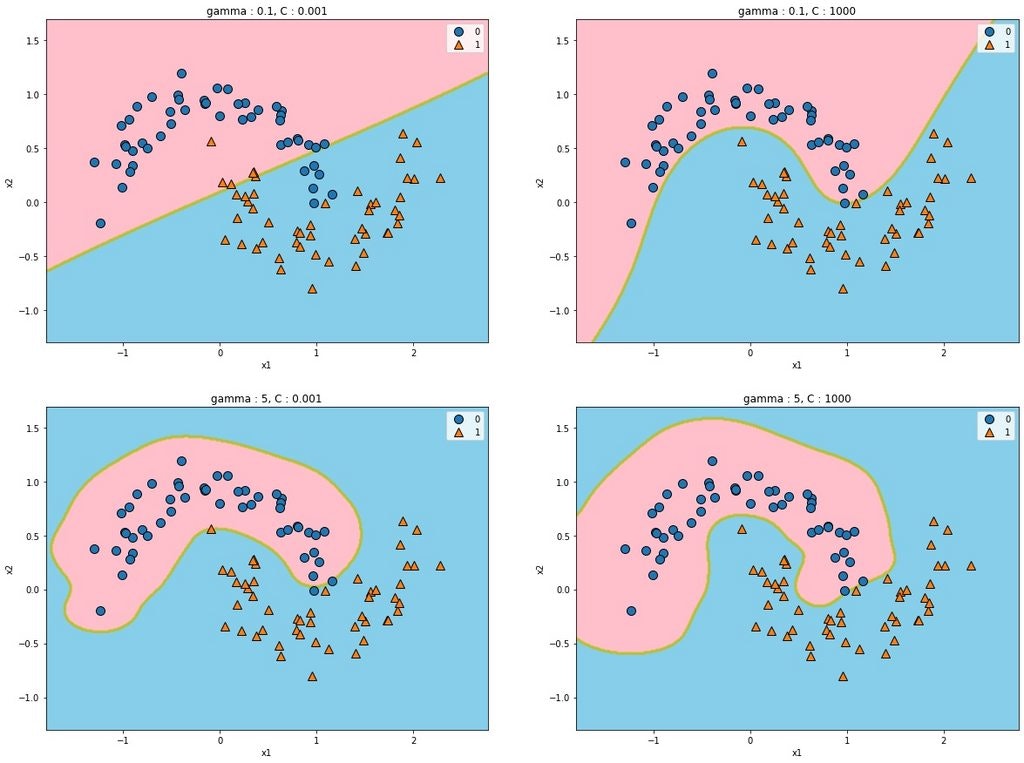
ガウスRBFカーネル

各サンプルに対してガウスRBFという分布を用いて、類似性特徴量を求める事を
カーネルトリックを使って計算量を落としたやり方。
元の特徴量を捨て(本当の意味では捨ててない)サンプル数ごとに分布(影響領域)を定めそれによって決定領域を描く。
カーネルの式は
$$k(x_1,x_2)=exp(\gamma||x_1 - x_2||^2)$$

$\gamma$をあげると各インスタンスが持つ影響領域が小さくなる。そのため過適合しやすくなる。
$C$をあげると誤差のペナルティが大きくなるので、過適合する。

rbf_karnel_svm = Pipeline([
    ('sclear', StandardScaler()),
    ('svm', SVC(kernel='rbf', gamma=gamma, C=C, random_state=0))
])

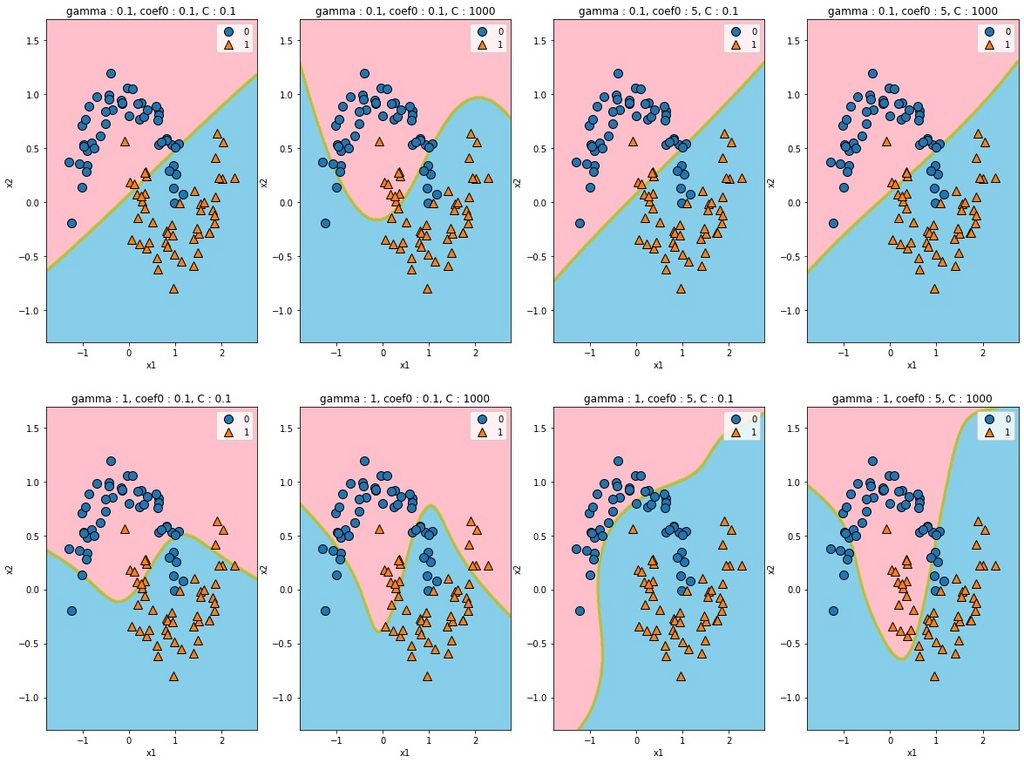
シグモイドカーネル

gammaをあげると適合はするものの、過適合になるというよりかはずれていくイメージ。
切片はそのままのイメージ、累乗すると複雑になる。
$$k(x_1,x_2)=tanh(\gamma x_1^Tx_2'+r)$$