はじめに
今回の記事はシリーズ物です。他の記事はこちら↓
0.設計編(キーを判別するAIとは?)
1.データ収集(クローリング)
2.データ整形(スクレイピング)
4.Djangoを用いたWebアプリ開発
開発から3-4ヶ月経ってしまいました。
開発当時はデプロイすることが目的になっていて、肝心のモデル選びに関してはあまり時間を割いていませんでした。
というわけで今回は様々なアプローチを試して、精度の比較を行いたいと思います。機械学習を使わず、ルールベースでの精度も求めてみます。
タスク確認
今回のタスクは、楽曲のコード進行からキーを判別することです。コード進行?キー?って方は↓の記事を御覧ください。
データ収集からAI開発、Webアプリ公開まで全てPythonで済ませた話(0.設計編)
データの確認
J-Total Musicというコード譜掲載サイトから、コードの出現回数とキーをスクレイピングしました。掲載されている曲のうち、キーが取得できた曲(20848曲)分のデータがあります。
ただし、楽曲によってはコードがほとんど掲載されていないものもあります。
例:https://music.j-total.net/data/012si/071_shinohara_tomoe/001.html
こうした楽曲は訓練データに相応しくないので、曲中の総コード出現数が20回以下のデータは落としてしまいます。また外れ値除去として、曲中の総コード出現数が250以上のデータも落とします。
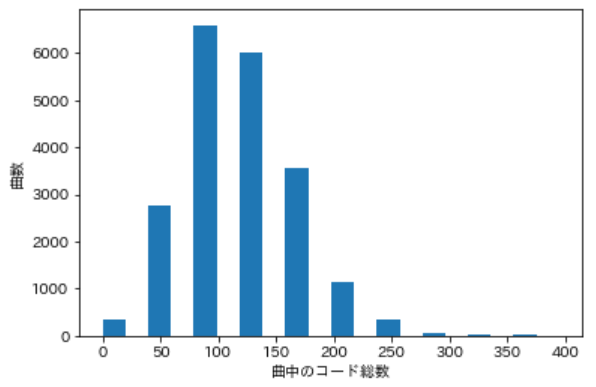
以下では、残った20481曲のデータを基に色々やっていきます。
データのイメージ
こんな感じです。
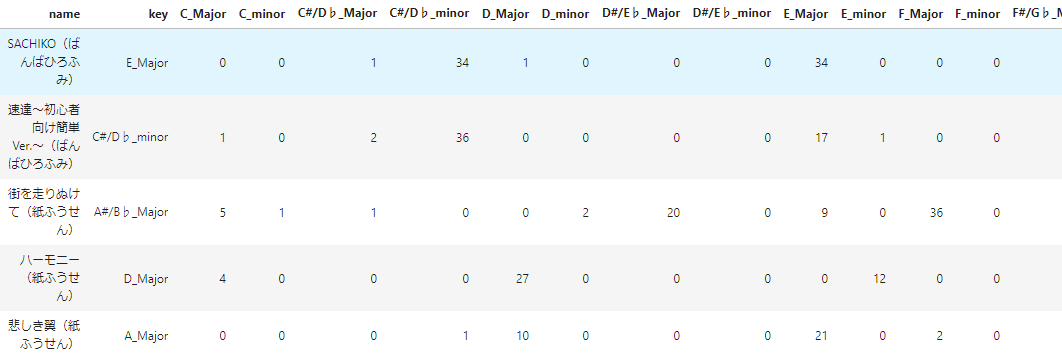
keyが被説明変数、keyから右が説明変数になっています。機械学習モデルに突っ込むために、keyをラベルエンコーディングして0から23の数値に変更します。他はそのまま使用します。
データ(クラス)の偏り
キーは全部で24種類あるのですが、もちろんデータ数は均等ではありません。
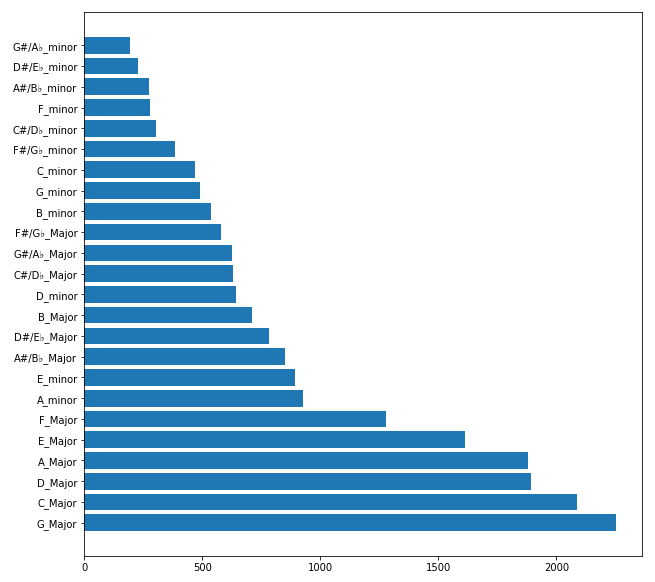
一番多いキーと一番少ないキーでは10倍近くの差があります。所謂不均衡データほどではないですが、少し気になります。
ちなみに長調(メジャーキー)と短調(マイナーキー)の割合は14955:5526 で、73%が長調の曲です。上のグラフを見ると、下位に短調がかたまっているのが分かります。
試したいこと
様々なアプローチを試してみて、その精度を確認します。
- ルールベースで分類
-
機械学習で分類
2-1. 24クラス分類
2-2. ドメイン知識を活かして問題設計を変える
比較用の指標とテストデータ
マルチクラス分類に関する評価指標に関しては、以下のページに詳しく書いてあります。
https://analysis-navi.com/?p=553
算出する値は以下の3つと、クラスごとの正答率を求めます。
- 正答率(正解数/データ数)
- マクロ再現率(各クラスごとの正答率の平均)
- マクロF1スコア(各クラスごとのF1スコアの平均)
テストデータですが、sklearnのtrain_test_splitで全体の25%のデータ(およそ5000曲)を用意します。データによる精度のバラツキを考慮し、5回平均の値を算出します。
また、別のテストデータとしてU-fretに掲載のflumpoolの楽曲90曲で正答率を確認します。これは自分がflumpoolが好きで、なおかつ全曲のキーを把握しているからです。以下このデータはfpデータと記載します。
結果
長くなるので先に結果をまとめます。
| 指標 | ルールベース1 | ルールベース2 | ロジスティック回帰 | サポートベクターマシン | LightGBM | LGBM × LGBM |
|---|---|---|---|---|---|---|
| 正答率 | 0.528 | 0.613 | 0.843 | 0.854 | 0.857 | 0.839 |
| マクロ再現率 | 0.566 | 0.626 | 0.836 | 0.832 | 0.836 | 0.826 |
| マクロF1スコア | 0.567 | 0.581 | 0.82 | 0.827 | 0.833 | 0.812 |
| fpデータ正答率 | 0.178 | 0.611 | 0.889 | 0.889 | 0.911 | 0.867 |
LightGBMが最も精度が高い!
1. ルールベースで分類
開発当時は「とりあえず機械学習を使って何かやりたい!」がモチベーションだったため機械学習を使いましたが、そもそもルールベースで解決できる問題かもしれません。
以下の2つを試してみます。
1-1. 曲中で最も使用回数の多いコード(以下、最頻コードと呼ぶ)をキーとする
1-2. 各キーのダイアトニックコードのコード総数を求めて、一番多かったキーを出力する
1-1. 最頻コードをキーとする
曲中で最も使用されているコードをキーであるとします。
例えば、曲中で「Dm」が一番多く使用されていたら、その曲のキーをDmと判別する、ということです。単純ですね。
もし最頻コードが複数ある場合、キーはランダムで決めようと思います。
コード
import random
def mode_pred(data):
# 最頻コードを求めて、そのコード名を保存
tmp_max = -1
for c in num_cols:
if tmp_max < data[c]:
ans = [c]
tmp_max = data[c]
elif tmp_max == data[c]:
ans.append(c)
# 最頻コードが複数ある場合、ランダムに選ぶ
if len(ans) == 1:
return ans[0]
else:
return random.choice(ans)
df['mode_pred'] = df.apply(mode_pred, axis=1)
結果
-
5回平均
正答率:0.528
マクロ再現率:0.556
マクロF1スコア:0.567 -
fpデータ
正答率:0.178
クラスごと正当率(再現率)
| キー | 正答率(再現率) |
|---|---|
| C_minor | 0.763 |
| F_minor | 0.747 |
| G_minor | 0.699 |
| D_minor | 0.684 |
| B_minor | 0.681 |
| A_minor | 0.676 |
| D#/E♭_minor | 0.668 |
| C#/D♭_minor | 0.663 |
| E_minor | 0.663 |
| A#/B♭_minor | 0.654 |
| F#/G♭_minor | 0.641 |
| G#/A♭_minor | 0.611 |
| E_Major | 0.522 |
| G_Major | 0.504 |
| A_Major | 0.496 |
| A#/B♭_Major | 0.494 |
| D_Major | 0.485 |
| C_Major | 0.483 |
| F_Major | 0.433 |
| F#/G♭_Major | 0.425 |
| B_Major | 0.412 |
| C#/D♭_Major | 0.408 |
| D#/E♭_Major | 0.402 |
| G#/A♭_Major | 0.379 |
クラスごとに見てみると、長調より短調の正答率が高いことが分かります。自分のドメイン知識と照らし合わせると、なんとなく納得できます。
fpデータの方はダメダメですね。。。長調の曲が多いことが原因と考えられます。
1-2. 各キーのダイアトニックコードのコード総数を計算する
以前の記事でも書いたのですが、僕がコード譜からキー判別をする際には、使用されているコードを眺めて「あのキーのダイアトニックコードが多く使われているから、あのキーだな」と判別しています。この方法を実装してみます。具体的には以下の流れです。
- 曲データから、各キーのダイアトニックコードの出現回数の合計を求める
- 1.で求めた合計が最も多いキーを曲のキーとする(複数ある場合はランダムで決める)
各行でfor文を24回(キーの数)だけ回すため、処理にかなり時間がかかります。5回平均を求めるのに、合計20分ほどかかりました。。。
コード
def diatonic_pred(data):
tmp_max = -1
# 各キーのダイアトニックコードの出現回数の合計を求める
for key, cols in diatonic_dict.items():
sum_value = data[cols].sum()
if tmp_max < sum_value:
ans = [key]
tmp_max = sum_value
elif tmp_max == sum_value:
ans.append(key)
# 判別
if len(ans) == 1:
return ans[0]
else:
return random.choice(ans)
tqdm_notebook.pandas()
df['diatonic_pred'] = df.progress_apply(diatonic_pred, axis=1)
結果
-
5回平均
正答率:0.613
クラスごと正答率の平均:0.626
F値:0.581 -
fpデータ
正答率:0.611
クラスごと正当率(再現率)
| キー | 正答率(再現率) |
|---|---|
| F_minor | 0.711 |
| G_minor | 0.702 |
| C_minor | 0.688 |
| A#/B♭_minor | 0.688 |
| A_minor | 0.67 |
| D_minor | 0.667 |
| G_Major | 0.651 |
| F#/G♭_minor | 0.649 |
| B_minor | 0.649 |
| E_minor | 0.633 |
| C#/D♭_minor | 0.632 |
| G#/A♭_minor | 0.615 |
| F_Major | 0.614 |
| G#/A♭_Major | 0.614 |
| A#/B♭_Major | 0.61 |
| B_Major | 0.61 |
| D#/E♭_Major | 0.607 |
| F#/G♭_Major | 0.604 |
| E_Major | 0.596 |
| D_Major | 0.586 |
| D#/E♭_minor | 0.579 |
| A_Major | 0.572 |
| C_Major | 0.566 |
| C#/D♭_Major | 0.504 |
最頻コードによる判別に比べ、平均した精度は高くなっています。正答率の最大値は70%程度でどちらの手法も同程度なのですが、最小値にかなり差があります。最頻コードの方では最も低い正答率は38%だったのですが、こちらの方法では50%になっています。また先程と同様、短調の曲の分類精度が高くなっています。
ここで混同行列を見てみましょう。
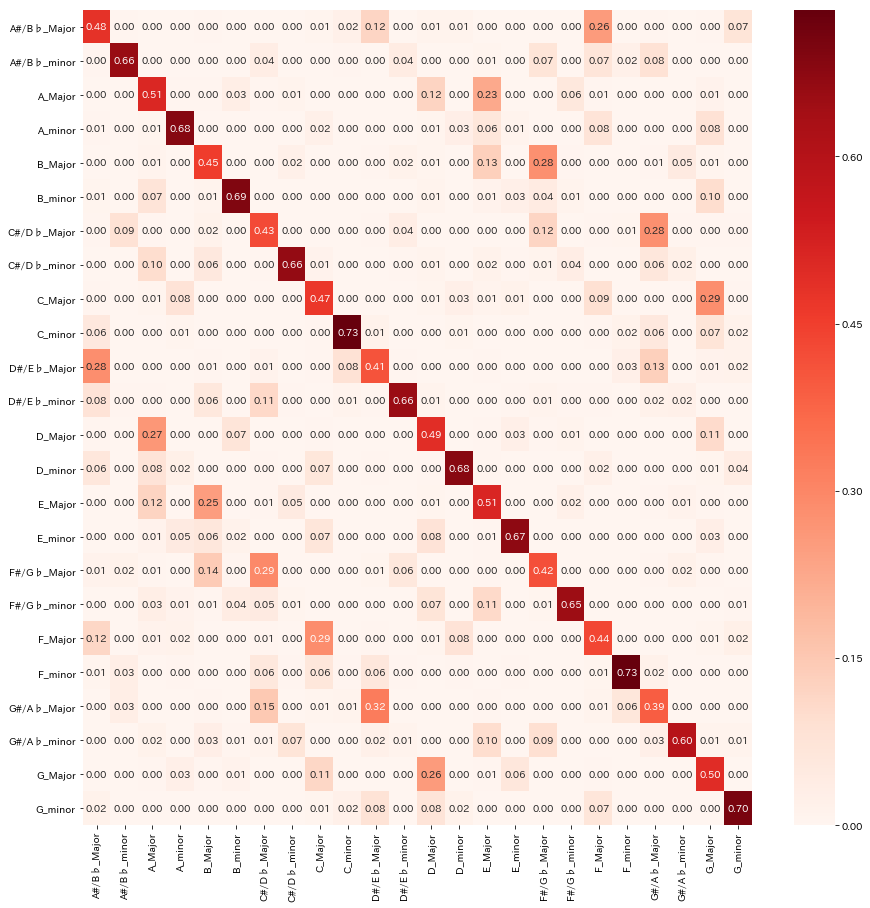
不思議なことに、各キーで決まって2割ほど誤分類しているキーがあります。これは平行調という、使用されるコードがほとんど同じキーに当たります。今回の判別方法はコードの使用回数を用いているため、平行調のキーに誤分類してしまうのは自然な結果なのかなと思います。
fpデータの正答率は先程に比べ大きく上昇したものの、6割程度です。誤分類データを見てみたのですが、そのほとんどが平行調に誤分類したものでした。この方法だと、平行調の分類が上手くいかないことが分かりました。
2. 機械学習で分類
ルールベースの精度が分かったところで、いよいよ機械学習を試してみましょう。こちらもいくつか手法を試してみようと思います。
2-1. 24クラス分類として判別を行う
2-2. ドメイン知識を活かして、問題設計を変える
2-1. 24クラス分類
素直に24クラスの分類問題として扱います。手法は古典的な線形分離アルゴリズム代表としてロジスティック回帰、非線形分離アルゴリズム代表としてサポートベクターマシン、精度の高さ・学習速度の速さ・前処理の少なさで最強との呼び声高いLightGBMを使います。手法の比較を行いたいので、派手なパラメータ調整は控えます。
train_test_splitでデータを分割し、そのままモデルに突っ込みます。
ハイパーパラメータの調整は行いませんが、class_weight=balancedとします。これを行うことで該当クラスのサンプル数 / (クラスの数 * 全サンプル数)で重み付けしてくれます。
ロジスティック回帰
一応、正則化項のパラメータを弄ってみたのですが、大きな差はなかったのでデフォルトで学習させています。
コード
for seed in [1, 4, 9, 16, 25]:
X_train, X_test, y_train, y_test = train_test_split(df[num_cols], df['target_key'], random_state=seed)
lr = LogisticRegression(class_weight='balanced')
lr.fit(X_train, y_train)
y_pred = lr.predict(X_test)
サポートベクターマシーン
試しに、カーネル関数にrbfカーネル、1対他分類法で学習させてみました。しかし学習には1時間近くかかるし、精度は平均30%程度と散々な結果でした。
サポートベクターマシンは変数の標準化を行うほうが良いので、変数の標準化+rbfカーネル+1対他分類法で精度を測ることにしました。標準化することによって実行時間が桁違いに早くなり、感動しました。とはいえ1回の学習に2-3分程度かかるので、他の2つに比べると実行時間は遅いです。
コード
from sklearn.svm import SVC
from sklearn.multiclass import OneVsRestClassifier
from sklearn.preprocessing import StandardScaler
# 1対他分類
svc = SVC(kernel='rbf', class_weight='balanced', verbose=True)
ovr = OneVsRestClassifier(svc)
# 標準化
sc = StandardScaler()
for seed in [1, 4, 9, 16, 25]:
X_train, X_test, y_train, y_test = train_test_split(sc.fit_transform(X), y, random_state=seed)
ovr.fit(X_train, y_train)
y_pred = ovr.predict(X_test)
LightGBM
デフォルトパラメータで実行しました。
コード
import lightgbm as lgbm
for seed in [1, 4, 9, 16, 25]:
X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=seed)
clf = lgbm.LGBMClassifier(class_weight='balanced')
clf.fit(X_train, y_train)
y_pred = clf.predict(X_test)
結果
| ロジスティック回帰 | サポートベクターマシン | LightGBM | |
|---|---|---|---|
| 正答率 | 0.843 | 0.854 | 0.857 |
| マクロ再現率 | 0.836 | 0.832 | 0.836 |
| マクロF1スコア | 0.820 | 0.827 | 0.833 |
精度に大きな差はないものの、LightGBMが最も精度が高いという結果になりました。
ただ、実行時間の観点ではLightGBM > ロジスティック回帰 >>> サポートベクターマシンという感じでした。5回の学習にかかる時間は、LightGBMは1分足らずで終わる一方でサポートベクターマシンは10分程度かかっていました。1回の学習にも時間がかかるので、あまりパラメータ調整も気軽にできないなという感じです。
次にクラスごと正答率を見てみましょう。
クラスごと正当率(再現率)
| キー | ロジスティック回帰 | サポートベクターマシン | LightGBM |
|---|---|---|---|
| C_Major | 0.838 | 0.866 | 0.856 |
| C_minor | 0.883 | 0.885 | 0.837 |
| C#/D♭_Major | 0.825 | 0.859 | 0.878 |
| C#/D♭_minor | 0.809 | 0.748 | 0.755 |
| D_Major | 0.84 | 0.875 | 0.871 |
| D_minor | 0.851 | 0.814 | 0.827 |
| D#/E♭_Major | 0.841 | 0.842 | 0.869 |
| D#/E♭_minor | 0.808 | 0.782 | 0.761 |
| E_Major | 0.871 | 0.897 | 0.9 |
| E_minor | 0.844 | 0.84 | 0.842 |
| F_Major | 0.851 | 0.857 | 0.87 |
| F_minor | 0.881 | 0.827 | 0.836 |
| F#/G♭_Major | 0.805 | 0.828 | 0.847 |
| F#/G♭_minor | 0.793 | 0.751 | 0.791 |
| G_Major | 0.857 | 0.872 | 0.872 |
| G_minor | 0.861 | 0.849 | 0.832 |
| G#/A♭_Major | 0.86 | 0.865 | 0.866 |
| G#/A♭_minor | 0.773 | 0.704 | 0.725 |
| A_Major | 0.849 | 0.874 | 0.887 |
| A_minor | 0.826 | 0.83 | 0.833 |
| A#/B♭_Major | 0.822 | 0.853 | 0.867 |
| A#/B♭_minor | 0.823 | 0.796 | 0.777 |
| B_Major | 0.815 | 0.847 | 0.855 |
| B_minor | 0.847 | 0.815 | 0.804 |
ロジスティック回帰は他の2つに比べ、短調のキーの正答率が高いことが読み取れます。
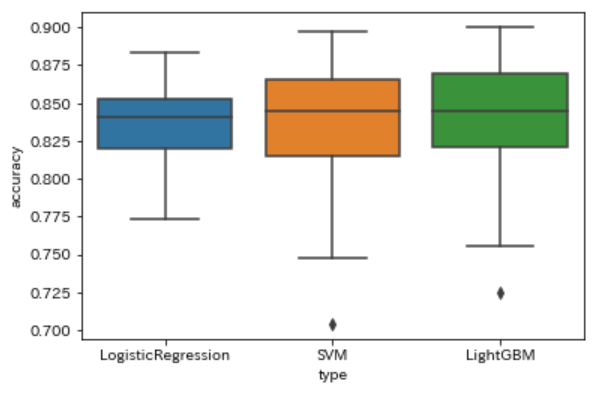
次に、各手法でキーごとの正答率を箱ひげ図でプロットしてみます。
どの手法でも最低正答率は70%以上となっています。ただ、ロジスティック回帰は他の手法に比べ、精度のバラツキ(範囲)が小さいことが読み取れます。
一応各指標ではトップだったLightGBMですが、かなり範囲にムラがあることが分かります。
ちなみにfpデータの正答率ですが、どの手法も80/90曲くらいの正答率でした。間違っているものも、平行調の間違いがほとんどでした(他は転調する曲など)。
2-2. ドメイン知識を活かして問題設計を変える
今回の「キーを判別する」という目的に対して、ドメイン知識を活用して問題設計を変えてしまいます。
判別したいキーは24種類あるのですが、24種類全てが全く違う特徴を持っているわけではありません。各キーに対して、似た特徴(具体的には、調号が同じで使用される音やコードがほぼ同じ)を持つキーがただ1つ存在します。これを平行調と言います。
例えば、C(ハ長調)の平行調はAm(イ短調)です。必ず長調と短調が対応するようになっています。実際にコード譜を見てみましょう。
どうでしょうか?使用されているコードがかなり似ていますよね。24種類のキーのうち、このようなキーの組み合わせが12種類存在します。
以上を踏まえて、以下のようにして判別を行います。
- 平行調でまとめた12クラス分類を行う
- 長調か短調か2値分類する。1の結果と合わせてキーを判別する。
分かりづらいので例を出すと
- 1の分類結果が「C(ハ長調)もしくはAm(イ短調)」で、2の分類結果が「長調」→キーはC(ハ長調)
- 1の分類結果が「F(ヘ長調)もしくはDm(ニ短調)」で、2の分類結果が「短調」→キーはDm(ニ短調)
こんな感じで判別を2回に分けるというイメージです。モデルはどちらもLightGBMを使用します。
コード
model_1 = lgbm.LGBMClassifier(class_weight='balanced')
model_2 = lgbm.LGBMClassifier(class_weight='balanced')
key_answer = df['key']
diatonic_answer = df['diatonic_type']
type_answer = df['key_type']
X = df[num_cols]
y1 = df['diatonic_type_int']
for seed in [1, 4, 9, 16, 25]:
# 12クラス分類(平行調の分類)
X_train, X_test, y1_train, y1_test = train_test_split(X, y1, random_state=seed)
model_1.fit(X_train, y1_train)
y1_pred = model_1.predict(X_test)
# 文字列(C_Major@A_minor)に戻す
y1_pred_str = le_d.inverse_transform(y1_pred)
# 同じデータで2値分類を行う(長調か短調か)
train_index = y1_train.index
test_index = y1_test.index
y2_train = type_answer[train_index]
y2_test = type_answer[test_index]
model_2.fit(X_train, y2_train)
y2_pred = model_2.predict(X_test)
# 12クラス分類と2値分類の結果を統合
y_pred = []
for y1_, y2_ in zip(y1_pred_str, y2_pred):
if y2_ == 1:
ans = y1_.split('@')[0]
else:
ans = y1_.split('@')[1]
y_pred.append(ans)
y_test = key_answer[test_index]
結果
-
5回平均
正答率:0.839
マクロ再現率:0.826
マクロF1スコア:0.812 -
fpデータ
正答率:0.867
クラスごと正答率
| キー | 正答率(再現率) |
|---|---|
| C_Major | 0.848 |
| C_minor | 0.843 |
| C#/D♭_Major | 0.858 |
| C#/D♭_minor | 0.853 |
| D_Major | 0.83 |
| D_minor | 0.825 |
| D#/E♭_Major | 0.84 |
| D#/E♭_minor | 0.836 |
| E_Major | 0.82 |
| E_minor | 0.815 |
| F_Major | 0.797 |
| F_minor | 0.787 |
| F#/G♭_Major | 0.811 |
| F#/G♭_minor | 0.803 |
| G_Major | 0.746 |
| G_minor | 0.686 |
| G#/A♭_Major | 0.775 |
| G#/A♭_minor | 0.764 |
| A_Major | 0.884 |
| A_minor | 0.875 |
| A#/B♭_Major | 0.909 |
| A#/B♭_minor | 0.89 |
| B_Major | 0.869 |
| B_minor | 0.864 |
5回平均の結果は、24クラス分類を行ったLightGBMの結果より少し下がっていますね。
1段階目(平行調でまとめた12クラス分類)の予測精度は93%程度で良かったものの、2段階目の長調or短調で全体の正答率は下がってしまっています。
fpデータに関してもやはり平行調の誤分類がほとんどを占めていました。ただ、24クラス分類であまり間違えなかった曲が数曲ありました。
まとめ
色々やってみましたが、LightGBMで素直に24クラス分類として予測させるのがベターという結果になりました。やっぱLightGBMはすごいです。
LightGBMがすごいのは精度だけではありません。学習速度がハンパなく早いです。そのためパラメータ調整など、他のモデルに比べて試行回数を増やすことができるのも大きなメリットだと思います。
LightGBM以外の手法がダメなわけではありません。例えばルールベース1では短調の正答率が高く、短調の分類には最頻コードが役立つことが分かりました。ルールベース2では自分の仮説の有効性を確認できました。ロジスティック回帰ではクラスごとの正答率のバラツキが小さいことが分かりました。サポートベクターマシンではパラメータ調整の余地がまだまだありますので、調整によっては正答率が上がるかもしれません。最後にやった、問題設計を変えた2段階予測も、モデルやパラメータ次第では良い結果が得られるかもしれません。
というわけで、現状は手軽に高精度を出せるLightGBMを使おうと思いますが、いずれ時間をかけてパラメータ調整を行ってみようと思います。その時は再度記事を書こうと思います。
稚拙な文章でしたが、お読みいただきありがとうございました。