Pythonでカスタム状態空間モデル

はじめに

状態空間モデルの中でもカスタムモデルについて日本語で解説したサイトが少なかった（私は見つけられなかった）ので、自身が色々と調べた結果を投稿します。

statsmodels（特にカスタム状態空間モデル）はモデルの定義が大変なので、その辺りに苦労しました。

間違った記述などあれば、ご指摘いただければ幸いです。

状態空間モデルとは

• 元々は物理モデルやシステム同定、制御分野などで使用されており、有名なのはロケットの軌道の推定と修正制御に使用されていたこと。また、状態空間モデルの論文を検索していると絶滅危惧種の動物の数の推定や、生存分析などで利用されています。使用例はstasmodelsのGithubのページを参照してください。
• 時系列解析にベイズ統計の要素を加えたものという解釈もできると思います。
• 一番の特徴は見えない「状態」を推定できることです。センサなどで観測したデータにはノイズ（主にセンシング誤差など）が含まれていると考え、そのデータの真の状態を推定します。（本当の真の状態は神のみぞ知る。）
  

観測方程式と状態方程式

モデルの構造は、観測方程式（観測モデルという記述の文献もあり）と状態方程式（システムモデルという記述の文献もあり）から成っています。

観測方程式：$y_t = Z_t (x_{t}) + d_t + \epsilon_t$
状態方程式：$x_{t+1} = T_t (x_{t}) + c_t + R_t \eta_{t}$

• $y_t$ : t時点の観測値（例：ノイズを含んだセンシング値）
• $Z_t$ : $x_t$を表す関数です。線形関数の場合は観測行列と呼ばれますが、要は行列形状の係数という認識でいいと思います。statsmodelsのドキュメントでは「Design matrix」と呼んでいます。
• $x_t$ : t時点の状態（ノイズの無い、見えない「状態」）
• $d_t$ : 観測方程式の切片
• $\epsilon_t$ : 観測ノイズ（例：センシング誤差）
• $x_{t+1}$ : t+1時点の状態
• $T_t$ : $x_t$を表す関数です。線形関数の場合は状態推移行列と呼ばれますが、要は行列形状の係数という認識でいいと思います。statsmodelsのドキュメントでは「Transition matrix」と呼んでいます。
• $c_t$ : 状態方程式の切片
• $R_t$ : $\eta_{t}$に掛かる係数。statsmodelsのドキュメントでは「Selection matrix」と呼んでいます。
• $\eta_{t}$ : 状態ノイズ

過去と現在と未来

詳細解説は省きますが、状態空間モデルでは、過去・現在・未来に対し、下記のような推定をします。

• 過去 : 固定区間平滑化
• 現在 : フィルタリング
• 未来 : 1期先（1時点先）予測
  すごいですね。

カスタムモデルの意義

状態空間モデルの中でもカスタムモデルの意義は下記のようなことにあります。

• 状態空間モデルの真の力は、カスタムモデルの作成と推定を可能にすることです。（statsmodelsのカスタムモデルの説明ページの引用（Google翻訳））
• 状態空間モデルとは、「たくさんの統計モデルを統一的に表すことができる統計モデル」なのです。だから状態空間モデルが注目を浴びてきているのです。（馬場さんのサイトlogics of blueの引用）
• 私は、時系列解析に物理的なモデルを組み込むことにより解釈可能なモデルを構築することができることだと思っています。

今回使用するモデル

観測方程式 :
　$y_t = x_{t} + \epsilon_t, \hspace{10pt}\epsilon_t\sim N(0,H_t)$
状態方程式 :
　$x_{t} = T_t x_{t-1} + A\cdot\exp\left(\frac{B}{z}\right) + \eta_{t}, \hspace{10pt}\eta_{t}\sim N(0,Q_t)$

上記にある式との違いは、観測方程式において$Z_t$を固定値にしたことと定数項の$d_t$を省いたこと、状態方程式の定数項の$c_t$の部分を$A\cdot\exp\left(\frac{B}{z}\right)$に置き換えています。

• A : 定数
• B : 定数
• z : 外生変数(exogenous variable)

※外生変数とは ： 一般的に時系列解析において予想したい未来の数値（目的変数）の過去のデータを用いて作られる変数（説明変数）を内生変数と呼ぶのに対し、それ以外の変数を外生変数と言います。

ライブラリインポートなど

さてここからPythonコードです。

import numpy as np
import pandas as pd
import datetime
import statsmodels.api as sm
import matplotlib.pyplot as plt
%matplotlib inline
plt.rc("figure", figsize=(16,8))
plt.rc("font", size=15)

テスト用のデータ作成

テスト用のデータを作成します。
（実際に使うときは、このような作業は不要なので、詳細解説は省きます。）

def gen_data_for_model1():
    nobs = 1000

    rs = np.random.RandomState(seed=93572)

    Ht = 5
    Tt = 1.001
    A = 0.1
    B = -0.007
    Qt = 0.01
    var_z = 0.1

    et = rs.normal(scale=Ht**0.5, size=nobs)
    z = np.cumsum(rs.normal(size=nobs, scale=var_z**0.05))
    Et = rs.normal(scale=Qt**0.5, size=nobs)

    xt_1 = 50
    x = []
    
    for i in range(nobs):
        xt = Tt * xt_1
        x.append(xt)
        xt_1 = xt
    xt = np.array(x)
    xt = xt + A * np.exp(B/z) + Et
    yt = xt + et
    
    return yt, xt, z

yt, xt, z = gen_data_for_model1()
_ = plt.plot(yt,color = "r")
_ = plt.plot(xt, color="b")

データをDataFrameに格納。予測をするためにindexをdatetimeにする

df = pd.DataFrame()
df['y'] = yt
df['x'] = xt
df['z'] = z
st = datetime.datetime.strptime("2001/1/1 0:00", '%Y/%m/%d %H:%M')
date = []
for i in range(1000):
    if i == 0:
        d = st
    dt = d.strftime('%Y/%m/%d %H:%M')
    date.append(dt)
    d += datetime.timedelta(days=1)
df['date'] = date
df['date'] = pd.to_datetime(df['date'] )
df = df.set_index("date")
df

モデルの定義

class custom(sm.tsa.statespace.MLEModel):
    param_names = ['T', 'A', 'B', 'Ht', 'Qt'] #推定するパラメータを指定
    start_params = [1., 1., 0., 1., 1] #推定するパラメータの初期値

    def __init__(self, endog, exog):
        exog = np.squeeze(exog)
        super().__init__(endog, exog=exog, k_states=1, initialization='diffuse')
        self.k_exog = 1
        
        # Z = I,上記式のZtに当たる部分は今回単位行列になる
        self['design', 0, 0] = 1.
        # R = I,上記式のRtに当たる部分は今回単位行列になる
        self['selection', 0, 0] = 1.
        
        # c_tを時変に設定します
        self['state_intercept'] = np.zeros((1, self.nobs))
        
    def clone(self, endog, exog, **kwargs):
        return self._clone_from_init_kwds(endog, exog=exog, **kwargs)
        
    def transform_params(self, params):
        # 分散は正数である必要があるので一旦2乗する
        params[3:] = params[3:]**2
        return params
        
    def untransform_params(self, params):
        # 2乗したものを1/2乗して元の大きさに戻す（平方根）
        params[3:] = params[3:]**0.5
        return params
    
    def update(self, params, **kwargs):
        # 更新するための指定です
        params = super().update(params, **kwargs)
        # T = T
        self['transition', 0, 0] = params[0] 
        # c_t = A * exp(B / z_t)
        self['state_intercept', 0, :] = params[1] * np.exp(params[2] / self.exog)       
        # Ht
        self['obs_cov', 0, 0] = params[3]
        # Qt
        self['state_cov', 0, 0] = params[4]

推定用データと予測用データに分ける

df_test = df.iloc[:800,:]
df_train = df.iloc[800:,:]

学習、サマリー確認

mod = custom(df_test['y'], df_test['z'])
res = mod.fit()
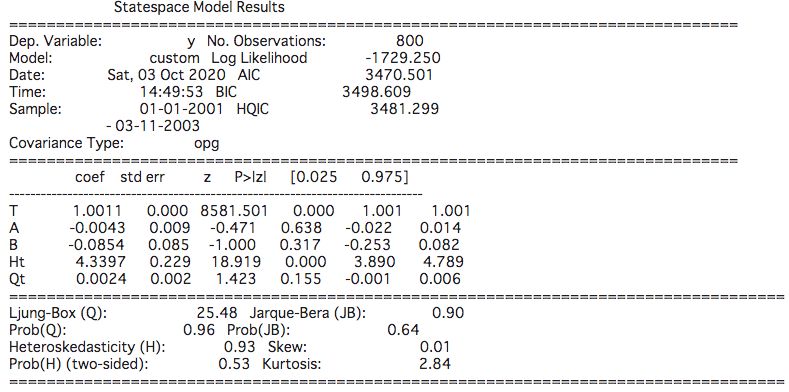
print(res.summary())

coefの部分が推定値ですが、はじめに作ったデータの数値と近いですね。

推定結果をDataFrameに格納

ss = pd.DataFrame(res.smoothed_state.T, columns=['x'], index=df_test.index)

推定と予測

predict = res.get_prediction()
forecast = res.get_forecast(df.index[-1], exog = df_train['z'].values)

予測する場合は、どの時点まで予測するかを指定する必要があります。（今回はdf.index[-1]で指定）
また、外生変数をモデルに使用する場合は、予測の時に「exog=」の引数でデータを指定する必要があります。今回は全てがダミーデータですが、実際に予測で使用する場合は、過去のデータなどからダミーデータを作成する必要があります。データの間隔が不均一なデータは予測に使えません。
（同じく外生変数を使ったSARIMAXなども同じことが言えます）

可視化

fig, ax = plt.subplots()

y = df['y']

y.plot(ax=ax,label='y')
predict.predicted_mean.plot(label='x')
predict_ci = predict.conf_int(alpha=0.05)
predict_index = predict_ci.index
ax.fill_between(predict_index[2:], predict_ci.iloc[2:, 0], predict_ci.iloc[2:, 1], alpha=0.1)

forecast.predicted_mean.plot(ax=ax, style='r', label='forecast')
forecast_ci = forecast.conf_int()
forecast_index = forecast_ci.index
ax.fill_between(forecast_index, forecast_ci.iloc[:, 0], forecast_ci.iloc[:, 1], alpha=0.1)

legend = ax.legend(loc='best');
fig.savefig('custom_statespace.png')

水色の部分は推定の95%信頼区間で、ピンク色の部分は予測の95%信頼区間です。

参考文献

この記事は以下の情報を参考にして執筆しました。

• 馬場さんのサイト logic of blue
• Albertさんのサイト
• Pythonで一般ガウス状態空間モデル
• statsmodelsのカスタム状態空間モデルの説明
• statsmodelsのドキュメント

statsmodels開発者のChad Fulton氏に感謝！

状態空間モデルのオススメ書籍

上記に挙げている文献以外でのオススメ書籍も紹介します。比較的読みやすいもの順に記載しています。

• 見えないものをさぐる-それがベイズ　ツールによる実践ベイズ統計
  この本は、多分日本にある状態空間モデルのことを記述した本で一番易しい内容で、まずとっかかりとして、どんなものかを知るには一番だと思います。

• 予測にいかす統計モデリングの基本　ベイス統計入門から応用まで
  現統計数理研究所所長の樋口知之先生が執筆された本です。書籍の名称から状態空間モデルの記述があることを予想しにくいですが、状態空間モデルのことを丁寧に記載されています。

• 時系列分析と状態空間モデルの基礎―ＲとＳｔａｎで学ぶ理論と実装
  本投稿で何回も登場した馬場さんの本です。非常にわかりやすい良書です。手を動かして（コーディングしながら）学習したい人にはオススメです。

• [時系列解析―自己回帰型モデル・状態空間モデル・異常検知― ]
  (https://www.kyoritsu-pub.co.jp/bookdetail/9784320125018)
  多分、pythonで状態空間モデルのことを記述した書籍は日本ではまだこれしかないと思います。コーディングはできるようになりますが、ちょっとモヤモヤした内容で理解しにくいです。
  但し、本投稿のようなカスタムモデルにまではふれていません。

買ったけどまだ読んでない書籍たち。。。

• 基礎からわかる時系列分析
• 時系列解析入門
• 岩波データサイエンスVol.1
• 岩波データサイエンスVol.6

改訂履歴

2020年10月3日　：　初版