はじめに
正規化ガウス関数ネットワーク(Normalized Gaussian Network; NGnet)は、30 年以上前(1989年)に提案されたニューラルネットワークの1つです。
入力空間をユニット分割し、各ユニットで入力に対する出力を線形近似し、近似した各結果を正規化ガウス関数で重みづけ結合することによって、任意の関数を近似します。
多層パーセプトロンが1つのモデルで入出力の関係を近似する「大域モデル」なのに対して、NGnet は各ユニットで局所近似した結果を正規化ガウス関数で束ねて、全体の入出力関係を近似するため、「局所モデル」と言えるでしょう。
この記事では、NGnet を EM アルゴリズムで学習させる手法を取り上げ、これを Python で実装します。元ネタは、次の論文です。
Sato, M., & Ishii, S. (2000). On-line EM algorithm for the normalized Gaussian network.
Neural Computation, 12, 407-432.
https://citeseerx.ist.psu.edu/viewdoc/download?doi=10.1.1.37.3704&rep=rep1&type=pdf
この論文のメインは「オンライン」の EM アルゴリズムで NGnet を学習させることですが、バッチ学習がオンライン学習の前提となることから、序盤はバッチ学習を説明しています。そのため、まずはバッチ学習版を今回の記事で実装していきます(オンライン学習版は次回予定)
【GitHub】 https://github.com/hajime-f/NGnet
論文との整合性を重視した実装になっており、数値計算の高速化を考慮していませんので、実行速度が遅い点に注意👺
バグを見つけたら、ぜひ教えてください。
近似計算(未知の入力 x に対する出力 y を推測する)
いま、NGnet は入力空間を $M$ 個のユニットに分割しており、それぞれに正規化ガウス関数 $N_i(x)$ と線形モデル $W_ix$ とを割り当てているとします $(i=1,2,\cdots, M)$。
このとき、NGnet は、$N$ 次元ベクトルの入力 $x$ が与えられたとき、$D$ 次元ベクトルの出力 $y$ を次のように計算します(論文の式 (2.1))。
\begin{align}
y &= \sum_{i=1}^M N_i(x)W_ix \\
N_i(x) &= \frac{G_i(x)}{\displaystyle\sum_{j=1}^M G_j(x)} \\
G_j(x) &= \frac{1}{\sqrt{(2 \pi)^N det\;\Sigma_j}}\exp\biggl(-\frac{1}{2}(x-\mu_j)^T\Sigma_j^{-1}(x-\mu_j)\biggr)
\end{align}
ここで、
- $W_i$ は $D \times N$ 次元の線形回帰パラメータ行列
- $G_j(x)$ は $j$ 番目 $(j=1,2,\cdots, M)$ の $N$ 次元ガウス関数(平均:$\mu_j$, 共分散:$\Sigma_j$)
です。
(論文にはベースライン $b_i$ が登場しますが、上記数式からは省略しました。また、$N_i(x)$, $G_j(x)$ は、ともにスカラーです)
入力 $x$ に対する出力 $y$ を計算する Python プログラムを書くことを考えると、まずは、
- $W_i$($D \times N$ 次元の行列が $M$ 個)
- $\mu_j$($N$ 次元の平均ベクトルが $M$ 個)
- $\Sigma_j$($N \times N$ 次元の分散共分散行列が $M$ 個)
の3種類(3$M$ 個)のパラメータを numpy の array として確保すればよいことになります。
なので、$N$, $D$, $M$ を引数として、上記パラメータを初期化する処理を、クラス NGnet のコンストラクタとして次のように定義します。
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
import numpy.linalg as LA
import random
class NGnet:
mu = []
Sigma = []
W = []
N = 0
D = 0
M = 0
def __init__(self, N, D, M):
for i in range(M):
self.mu.append(2 * np.random.rand(N, 1) - 1)
for i in range(M):
x = [random.random() for i in range(N)]
self.Sigma.append(np.diag(x))
for i in range(M):
w = 2 * np.random.rand(D, N) - 1
w_tilde = np.insert(w, np.shape(w)[1], 1.0, axis=1)
self.W.append(w_tilde)
self.N = N
self.D = D
self.M = M
次に、上記数式を順番に計算する処理を書いていきます。
class NGnet:
...
def get_output_y(self, x):
y = np.array([0.0] * self.D).reshape(-1, 1)
# 式 (2.1a) の計算
for i in range(self.M):
N_i = self.evaluate_Normalized_Gaussian_value(x, i) # N_i(x)
Wx = self.linear_regression(x, i) # W_i * x
y += N_i * Wx
return y
# 式 (2.1b) の N_x(x) の計算
def evaluate_Normalized_Gaussian_value(self, x, i):
# 式 (2.1b) の分母の計算
sum_g_j = 0
for j in range(self.M):
sum_g_j += self.multinorm_pdf(x, self.mu[j], self.Sigma[j])
# 式 (2.1b) の分子の計算
g_i = self.multinorm_pdf(x, self.mu[i], self.Sigma[i])
# 式 (2.1b) の計算
N_i = g_i / sum_g_j
return N_i
# 式 (2.1c) の G_x(x) の計算
def multinorm_pdf(self, x, mean, cov):
Nlog2pi = self.N * np.log(2 * np.pi)
logdet = np.log(LA.det(cov))
covinv = LA.inv(cov)
diff = x - mean
logpdf = -0.5 * (Nlog2pi + logdet + (diff.T @ covinv @ diff))
return np.exp(logpdf)
# W_i * x の計算
def linear_regression(self, x, i):
x_tilde = np.insert(x, len(x), 1.0).reshape(-1, 1)
Wx = np.dot(self.W[i], x_tilde)
return Wx
以上のとおり、入力 $x$ に対する出力 $y$ を計算するプログラムが書けました。論文の式 (2.1) をプログラムとして書き下せばいいだけなので、ここまでは簡単です。
バッチ学習(モデルパラメータを最適化する)
入出力のペア $\{x_t, y_t,|,t=1,2,\cdots,T\}$ が学習データとして与えられたとき、NGnet はモデルパラメータを最適化することで $x$ と $y$ との関係 $f$ を学習します(関数近似)。
ここで、「そのペアがどのユニットから得られた学習データかは分からない」ことがポイントです。つまり、パラメータはユニットごとに存在するため、学習データが得られたユニットを特定できなければ、パラメータは本来学習できないのです。
仕方がないので、ユニット $i$ を隠れ変数とする EM アルゴリズムを使って、これを推定しながらパラメータを学習します。具体的には、次の2つのステップを繰り返します。
- Eステップ:ユニットに関する事後確率を計算する(どのユニットから得られた学習データかを確率的に推定する)
- Mステップ:計算した事後確率に応じてパラメータを更新する
Eステップ
Eステップでは、ユニット $i$ に関する事後確率を次のとおりに計算します(論文の式 (3.1))。
P(i\,|\,x(t),y(t),\theta)=\frac{P(x(t),y(t),i\,|\,\theta)}{\sum_{j=1}^{M}P(x(t),y(t),i\,|\,\theta)}
右辺の同時確率 $P(x(t),y(t),i,|,\theta)$ は、次のように計算します(論文の式 (2.2), (2.3))。
\begin{align}
P(x(t),y(t),i\,|\,\theta)&=P(i\,|\,\theta)\,P(x\,|\,i,\theta)\,P(y\,|\,x,i,\theta)\\
P(i\,|\,\theta)&=\frac{1}{M}\\
P(x\,|\,i,\theta)&=G_i(x)\\
P(y\,|\,x,i,\theta)&=(2\pi)^{-\frac{D}{2}}\sigma_i^{-D}\exp\biggl(-\frac{1}{2\sigma_i^{2}}|y-W_ix|^{2}\biggr)
\end{align}
ここで、$\theta=\{\mu_i,\Sigma_i, \sigma_i^2, W_i,|,i=1,2,\cdots,M \}$ です。
同時確率でパラメータ $\sigma_i^2$ が1種類増えたので、これをクラス変数に加えてコンストラクタで初期化します。また、事後確率 $P(i,|,x(t),y(t),\theta)$ を入れるための変数や、学習データの数を入れる変数もクラスに追加しておきます。
class NGnet:
...
var = []
posterior_i = []
T = 0
def __init__(self, N, D, M):
...
for i in range(M):
self.var.append(1)
そして、あとは式に記載のとおりに数値計算を実装していきます。
class NGnet:
...
def batch_learning(self, x_list, y_list):
if len(x_list) != len(y_list):
print('Error: The number of input vectors x is not equal to the number of output vectors y.')
exit()
else:
self.T = len(x_list)
self.posterior_i = []
self.batch_E_step(x_list, y_list) # E ステップ実行
self.batch_M_step(x_list, y_list) # M ステップ実行
# 式 (3.1) の計算
def batch_E_step(self, x_list, y_list):
for x_t, y_t in zip(x_list, y_list):
sum_p = 0
for i in range(self.M):
sum_p += self.calc_P_xyi(x_t, y_t, i)
p_t = []
for i in range(self.M):
p = self.calc_P_xyi(x_t, y_t, i)
p_t.append(p / sum_p)
self.posterior_i.append(p_t)
# 式 (2.2) の計算
def calc_P_xyi(self, x, y, i):
# 式 (2.3a) の計算
P_i = 1 / self.M
# 式 (2.3b) の計算
P_x = self.multinorm_pdf(x, self.mu[i], self.Sigma[i])
# 式 (2.3c) の計算
diff = y.reshape(-1, 1) - self.linear_regression(x, i)
P_y = self.norm_pdf(diff, self.var[i])
# 式 (2.2) の計算
P_xyi = P_i * P_x * P_y
return P_xyi
# 式 (2.3c) の計算
def norm_pdf(self, diff, var):
log_pdf1 = - self.D/2 * np.log(2 * np.pi)
log_pdf2 = - self.D/2 * np.log(var)
log_pdf3 = - (1/(2 * var)) * (diff.T @ diff)
return np.exp(log_pdf1 + log_pdf2 + log_pdf3)
ちなみに、$\sigma_i^2$ は2乗した状態でパラメータを持っているので($\sigma_i$ ではない)、実装時の帳尻合わせに注意が必要です。
Mステップ
M ステップでは、次を計算します(論文の式 (3.4), (3.5))。
\begin{align}
\mu_i&=\frac{<x>_i(T)}{<1>_i(T)}\\
\Sigma_i&=\frac{<(x-\mu_i)(x-\mu_i)^T>_i(T)}{<1>_i(T)}\\
W_i&=<yx^T>_i(T)[<xx^T>_i(T)]^{-1}\\
\sigma_i^2&=\frac{1}{D}\frac{<|y-W_ix|^2>_i(T)}{<1>_i(T)}\\
\end{align}
<> が見慣れない記法ですが、要するに、E ステップで計算したユニットの事後確率に関する期待値を計算するということです。次のプログラムを見れば分かるとおり、たいした計算をするわけではありません。
class NGnet:
...
# 式 (3.4) の計算
def batch_M_step(self, x_list, y_list):
self.batch_Sigma_update(x_list)
self.batch_mu_update(x_list)
self.batch_W_update(x_list, y_list)
self.batch_var_update(x_list, y_list)
# 式 (3.4a) の計算
def batch_mu_update(self, x_list):
for i in range(self.M):
sum_1 = 0
sum_mu = 0
for t, x_t in enumerate(x_list):
sum_1 += self.posterior_i[t][i]
sum_mu += x_t.T * self.posterior_i[t][i]
self.mu[i] = (sum_mu / sum_1).T
# 式 (3.4b) の計算
def batch_Sigma_update(self, x_list):
for i in range(self.M):
sum_1 = 0
sum_diff = 0
for t, x_t in enumerate(x_list):
sum_1 += self.posterior_i[t][i]
diff = x_t - self.mu[i]
sum_diff += (diff @ diff.T) * self.posterior_i[t][i]
self.Sigma[i] = sum_diff / sum_1
# 式 (3.4c) の計算
def batch_W_update(self, x_list, y_list):
alpha_I = np.diag([0.00001 for i in range(self.N+1)]) # Regularization
for i, W_i in enumerate(self.W):
sum_xx = 0
sum_yx = 0
for t, (x_t, y_t) in enumerate(zip(x_list, y_list)):
x_tilde = np.insert(x_t, len(x_t), 1.0).reshape(-1, 1)
sum_xx += (x_tilde * x_tilde.T * self.posterior_i[t][i]) / self.T
sum_yx += (y_t * x_tilde.T * self.posterior_i[t][i]) / self.T
self.W[i] = sum_yx @ LA.inv(sum_xx + alpha_I)
# 式 (3.4d) の計算
def batch_var_update(self, x_list, y_list):
for i, var_i in enumerate(self.var):
sum_1 = 0
sum_diff = 0
for t, (x_t, y_t) in enumerate(zip(x_list, y_list)):
sum_1 += self.posterior_i[t][i]
diff = y_t - self.linear_regression(x_t, i)
sum_diff += (diff.T @ diff) * self.posterior_i[t][i]
self.var[i] = (1/self.D) * (sum_diff / sum_1)
$W_i$ の更新のところで、ごく小さな単位行列(alpha_I)を足しています。これは、逆行列を計算するときにランク落ちしないように、誤差が出ない範囲で手当てするための計算テクニックです。
繰り返し計算
あとは学習データを用意し、対数尤度に変化がなくなるまで E ステップと M ステップとを繰り返せば、いい感じにパラメータが最適化されます。
次のサンプルプログラムでは、
- 入力 $x$:2次元
- 出力 $y$:1次元
- ユニット数:20
- 学習データ数:1000
- 未知データ:1000
と設定しています。
if __name__ == '__main__':
N = 2
D = 1
M = 20
learning_T = 1000
inference_T = 1000
ngnet = NGnet(N, D, M)
# 学習データを準備する
learning_x_list = []
for t in range(learning_T):
learning_x_list.append(20 * np.random.rand(N, 1) - 10)
learning_y_list = []
for x_t in learning_x_list:
learning_y_list.append(np.array(func1(x_t[0], x_t[1])))
# モデルパラメータを最適化する
previous_likelihood = -10 ** 6
next_likelihood = -10 ** 5
while abs(next_likelihood - previous_likelihood) > 5:
ngnet.batch_learning(learning_x_list, learning_y_list)
previous_likelihood = next_likelihood
next_likelihood = ngnet.calc_log_likelihood(learning_x_list, learning_y_list)
print(next_likelihood)
if previous_likelihood >= next_likelihood:
print('Warning: Next likelihood is smaller than previous.')
# 未知の入力 x に対する出力 y を推測する
inference_x_list = []
for t in range(inference_T):
inference_x_list.append(20 * np.random.rand(N, 1) - 10)
inference_y_list = []
for x_t in inference_x_list:
inference_y_list.append(ngnet.get_output_y(x_t))
シミュレーション結果
というわけで、評価関数を用意し、グラフをプロットして NGnet の近似能力をみてみましょう。
class NGnet:
...
# 対数尤度の計算→この値が1以下になるまで EM を繰り返し
def calc_log_likelihood(self, x_list, y_list):
log_likelihood = 0
for x_t, y_t in zip(x_list, y_list):
p_t = 0
for i in range(self.M):
p_t += self.calc_P_xyi(x_t, y_t, i)
log_likelihood += np.log(p_t)
return log_likelihood.item()
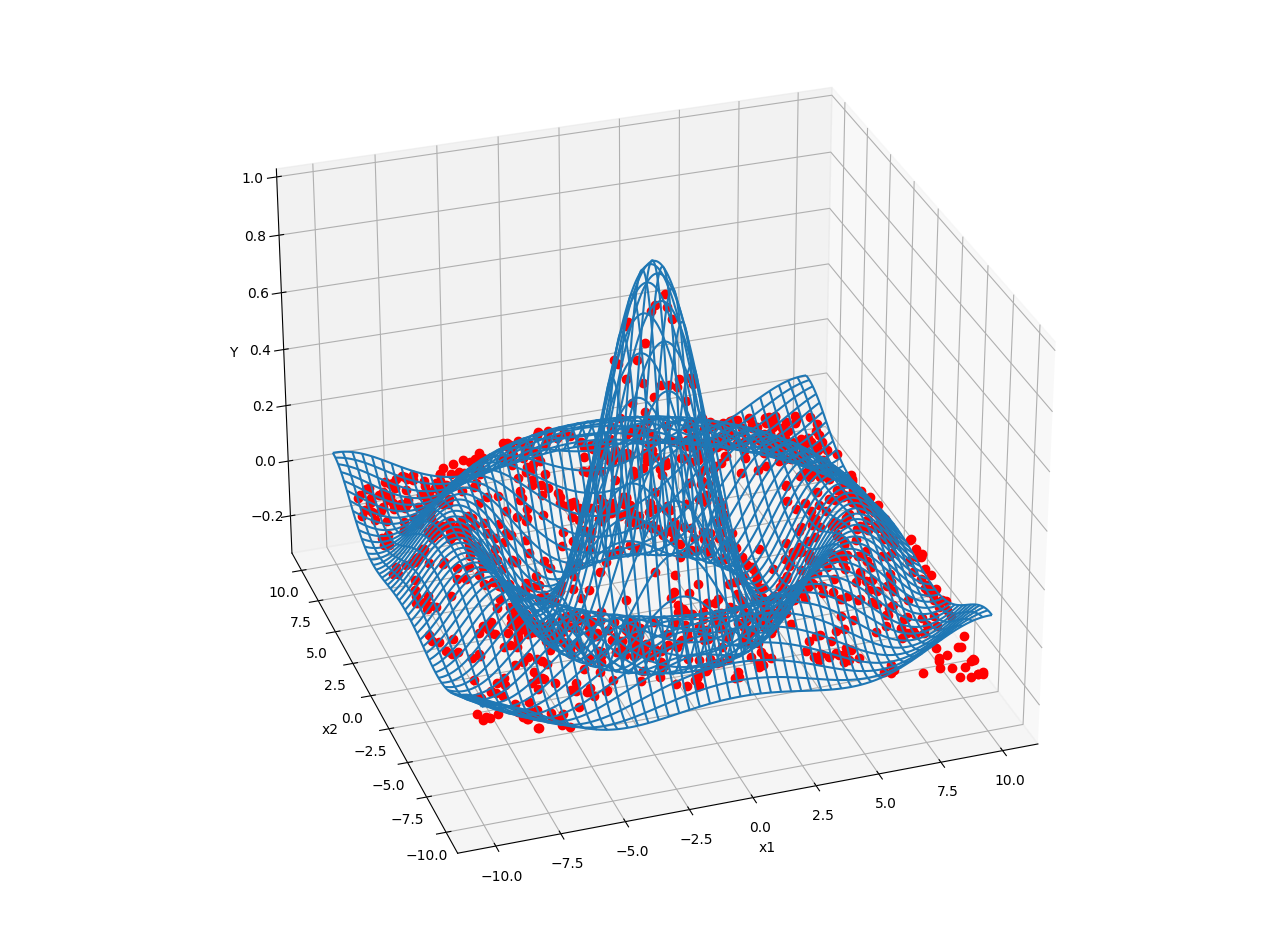
# 評価用関数1
def func1(x_1, x_2):
s = np.sqrt(np.power(x_1, 2) + np.power(x_2, 2))
return np.sin(s) / s
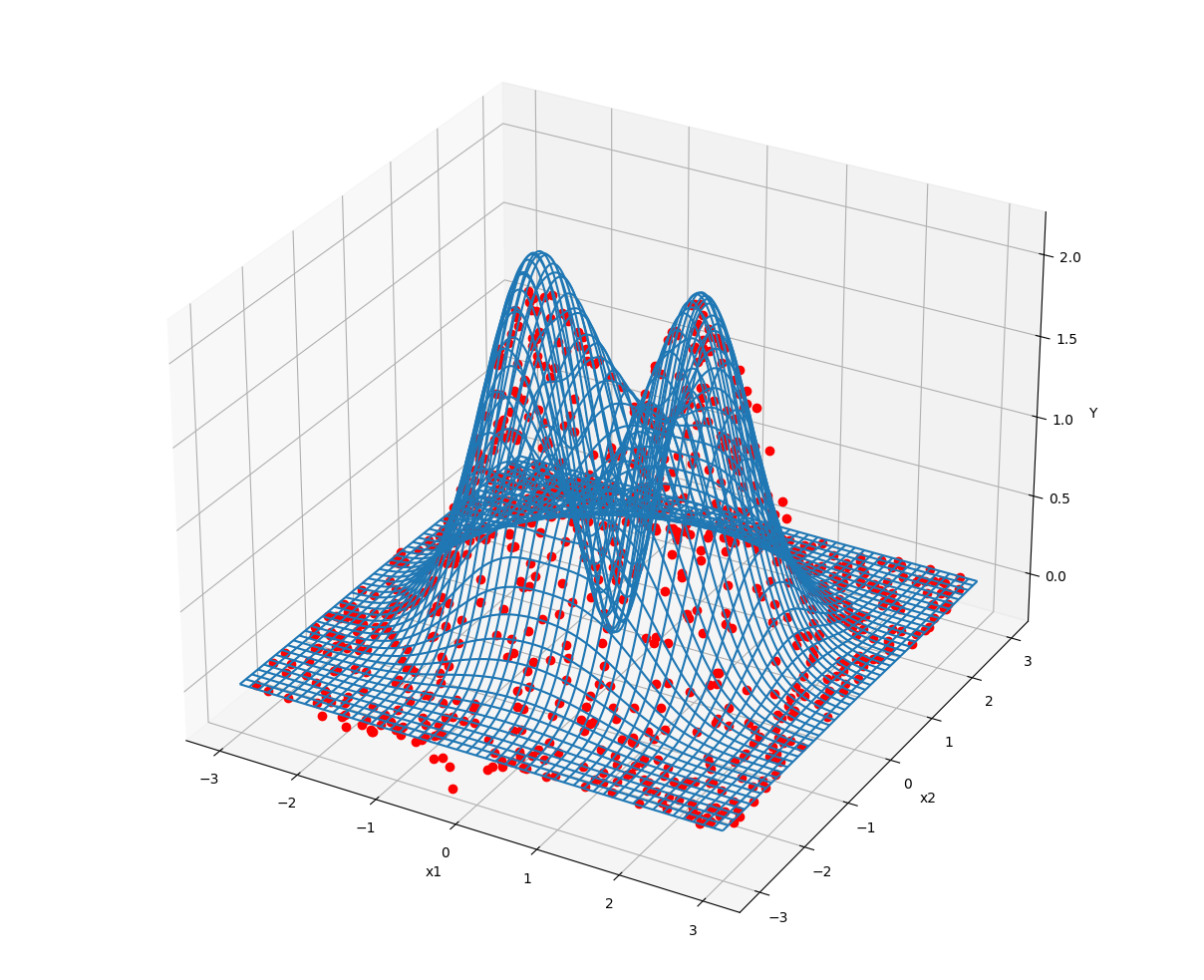
# 評価用関数2
def func2(x_1, x_2):
xx1 = np.power(x_1, 2)
xx2 = np.power(x_2, 2)
return 3 * np.power(np.e, -xx1-xx2) * (2 * xx1 + xx2)
if __name__ == '__main__':
...
# グラフの出力
x1_list = []
x2_list = []
y1_list = []
for x_t, y_t in zip(inference_x_list, inference_y_list):
x1_list.append(x_t[0].item())
x2_list.append(x_t[1].item())
y1_list.append(y_t.item())
X1_appx = np.array(x1_list)
X2_appx = np.array(x2_list)
Y1_appx = np.array(y1_list)
x1_real = np.arange(-10.0, 10.0, 0.02)
x2_real = np.arange(-10.0, 10.0, 0.02)
X1_real, X2_real = np.meshgrid(x1_real, x2_real)
Y1_real = func1(X1_real, X2_real)
fig = plt.figure()
ax = Axes3D(fig)
ax.set_xlabel("x1")
ax.set_ylabel("x2")
ax.set_zlabel("Y")
ax.plot_wireframe(X1_real, X2_real, Y1_real)
ax.plot(X1_appx, X2_appx, Y1_appx, marker="o", linestyle='None', color="r")
plt.show()
グラフは次のとおり。いずれも青線が真の評価関数、赤点が NGnet が近似した結果を示します。
赤点(近似結果)が青線(真の評価関数)にへばりつくように表示されています。いい感じで近似できてますね。
まとめ
というわけで、この記事では、正規化ガウス関数ネットワーク(NGnet)をバッチ EM アルゴリズムで学習させる手法を実装してみました。
NGnet は、少ない学習データでも性能を発揮する優れた学習器で、ディープラーニング全盛の時代でも現役で実問題に適用されています。
今回のサンプルプログラムは GitHub で公開していますので、皆さん適当に遊んでみてください。