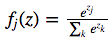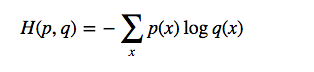ニューラルネットワークによく使われているロス関数Softmax-Cross-Entropyを簡単な例からイメージを掴もう。
まずは式
Softmax
Cross-Entropy
pは真の分布、qは推定分布
例：全結合層の出力が
[1,2,3,4]
Softmax関数を取るには、まず指数を取る
[2.718, 7.389, 20.085, 54.598]
そして合計を計算してから各値割合を計算
[0.033, 0.087, 0.236, 0.644] <- 推定分布
次にcross-entropyを計算
q -> [0.033, 0.087, 0.236, 0.644]
ケース1： p <- [0,0,0,1] 真の結果がクラス4の場合
H(p,q) = - log(0.644) = 0.44
ケース2： p <- [0,0,1,0] 真の結果がクラス3の場合
H(p,q) = -log(0.236) = 1.44
明らかにうまく予測できたケース(ケース1)の誤差が小さいことがわかった。
soft-cross-entropy誤差を最小化にしたら、予測結果が真に近く。