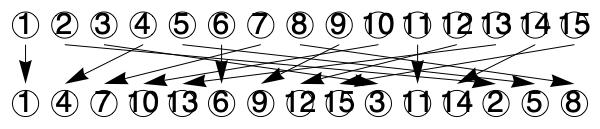
Prime-Factor FFT は要素数が互いに素な整数の掛け算になっているときに使える。添字の並び替えをして2DFFTをするだけというシンプルさが特徴である。
原理
以下にDFTの式を示す。
y_i = \sum_{j=0}^{n-1}x_j \omega_n^{-i j}
ここで $\omega_n = e^{2 \pi i/n}$ である。
要素数 $n$ が互いに素な整数 $n_1$,$n_2$の積であるとする ($n = n_1 n_2$) 。
ここで以下の式のように添字 $i,j$ を新しい添字の組 {$i_1,i_2$},{ $j_1,j_2$} に対応させる。
\begin{align}
i &= i_1 n_2 + i_2 n_1 \mod n, \\
j &= j_1 n_2^{-1} n_2 + j_2 n_1^{-1} n_1 \mod n,
\end{align}
$i$ の添字の対応はGood-mappingと呼ばれ、$j$ の添字の対応はCRT(Chinese Reminder Theorem)-mappingと呼ばれる。CRT-mappingの $n_1^{-1}$ は $n_1$ の 剰余 $n_2$ における乗法的逆元、つまり $n_1^{-1} n_1 = 1 \mod n_2$ を満たす数である。
また$n_2^{-1}$ も同様である。
これを使ってDFTの式を書き直すと、以下のようになる。
y_{i_1 n_2^{-1} n_2 + i_2 n_1^{-1} n_2 } = \sum_{j_1=0}^{n_1-1} \left( \sum_{j_2=0}^{n_2-1} x_{j_1 n_2 + j_2 n_1} \omega_{n_2}^{-i_2 j_2} \right) \omega_{n_1}^{-i_1 j_1}
ここで $\omega_{n_1} = e^{2 \pi i/n_1},\omega_{n_2} = e^{2 \pi i/n_2}$ である。
DFTの式の $\omega_n^{ij}$ は、$ij$ の $n$ の剰余で決まるので、$ij$ のうち $n$ の倍数になる項は消える。なので
\begin{align}
i j &= (i_1 n_2 + i_2 n_1)(j_1 n_2^{-1} n_2 + j_2 n_1^{-1} n_1) \mod n \\
&= i_1 j_1 (n_2 n_2^{-1} \mod n_1)n_2 + i_2 j_2 (n_1 n_1^{-1} \mod n_2) n_1 + (...)n_1 n_2 \mod n \\
&= i_1 j_1 n_2 + i_2 j_2 n_1
\end{align}
このようにしてDFTはサイズ$n_1 \times n_2$の二次元DFTに変換される。
Good mapping
i = i_1 n_2 + i_2 n_1 \mod n
例えば$n_1=3,n_2=5$のとき、$3\times5$の行列を作って、左上に1を置く。そのあと、列方向に移動するときに3、行方向を移動するときに5を足して数字を埋めていく。これを剰余15でやる。
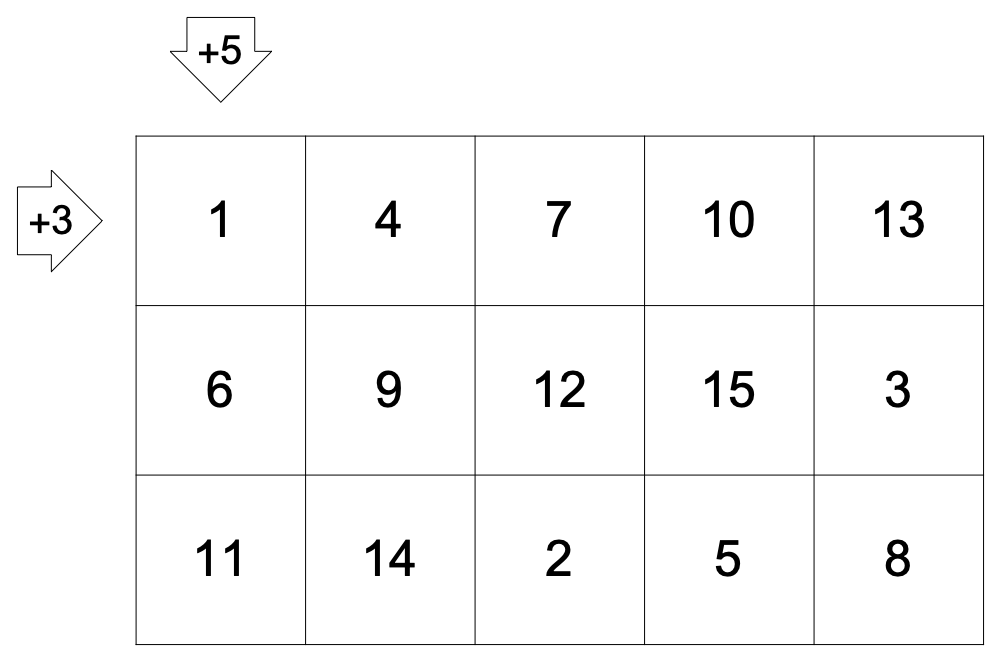
Prime-Factor FFT では要素数nの一次元FFTを$n_1\times n_2$の二次元FFTにするので並べ替えながら行列に数字を入れていくイメージになる。ただし、実際にはin-placeで計算を行いたいので二次元配列を生成したりせず、一次元の並べ替えを行う。
上の行列からは{1,4,7,10,13,6,9,12,15,3,11,14,2,5,8}という数列が得られる。これからGood mappingによる並び替えが求まる。
CRT mapping
j = j_1 n_2^{-1} n_2 + j_2 n_1^{-1} n_1 \mod n
この関係は中国の剰余定理(Chinese Remainder Theorem)に基づく(参考:中国剰余定理 (CRT) の解説と、それを用いる問題のまとめ)。
これは、$n$が互いに素な整数$n_1,n_2$の積であるとき、0から$n-1$までの整数はそれの$n_1$の剰余と$n_2$の剰余の組によって一義的に決定されるという定理である。
例えば$n_1=3,n_2=5$として、1から15までの数字の剰余3、剰余5を見るとつぎのようになる。
| n | mod 3 | mod 5 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 2 | 2 |
| 3 | 0 | 3 |
| 4 | 1 | 4 |
| 5 | 2 | 0 |
| 6 | 0 | 1 |
| 7 | 1 | 2 |
| 8 | 2 | 3 |
| 9 | 0 | 4 |
| 10 | 1 | 0 |
| 11 | 2 | 1 |
| 12 | 0 | 2 |
| 13 | 1 | 3 |
| 14 | 2 | 4 |
この表をみると、右の数字の組み合わせはそれぞれ一回ずつしか出てこない。つまり、剰余15の整数$j$は剰余3の整数$j_1$と剰余5の整数$j_2$の組{$j_1,j_2$}と一対一に対応するということが分かる。これは群論では $\mathbb{Z}/15\mathbb{Z} \cong \mathbb{Z}/3\mathbb{Z} \times \mathbb{Z}/5\mathbb{Z}$ と表される。これが中国の剰余定理である。
この対応関係を数式にしたものがはじめの式である。$3^{-1}$は$3\times2 = 6 = 1 \mod 5$なので$2$、$5^{-1}$は$5\times2=10=1 \mod3$なので$2$である。なので
j = j_1 2 \times 5 + j_2 2\times3 = -5 j_1 + 6 j_2 \mod 15
この関係はちゃんと上の表に当てはまっていることが分かる。ただし、CRT-mappingを計算するときはこの数式を計算するよりも、上の表を作ったときのようにして{$j_1,j_2$}を生成していくほうが簡単である。
$3\times5$の行列を作って、左上に1を置く。そこから右斜め下に進んで1を足すという仕方で数字を埋めていく。辺にぶつかったら”周期的境界条件”を使う。
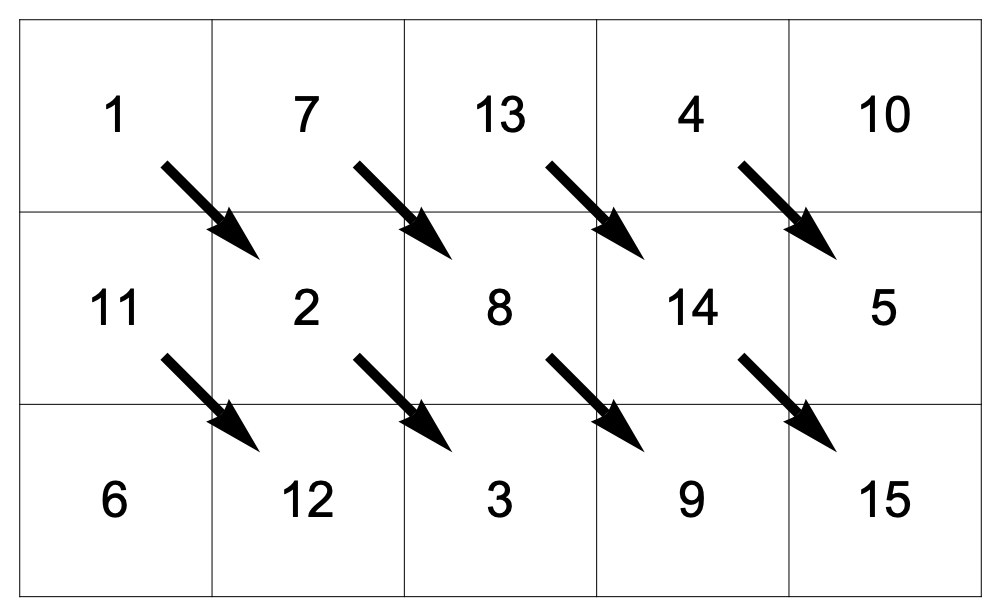
この行列から{1,7,13,4,10,11,2,8,14,5,6,12,3,9,15}という数列が得られる。

可視化
任意要素数の高速フーリエ変換で行った可視化をする。
FFT行列の行にGood-mapping、列にCTR-mappingの並び替えを施すと...

これは要素数5のFFTと要素数3のFFTが重なったものである。
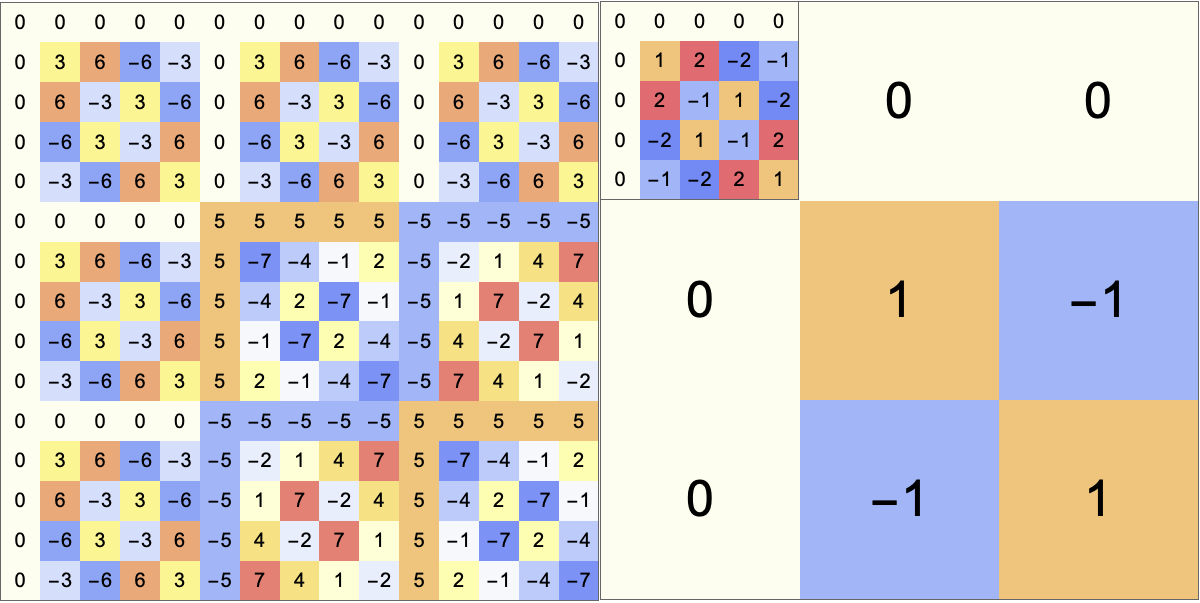
ちなみに列にGood-mapping、行にCTR-mappingの並び替えを施しても同じ結果が得られる。
実装
一段PFFFT
まず一番シンプルな、分解を一回だけするPFFFTを作る。
一段PFFFTコード
template<typename T> void fft_pf(T &array, int size, int sign, int n){
int m = size/n;
std::vector<Complex> temp(size),omega(size);
for(int i=0;i<size;i++){
omega[i].real(fft_cos(i,size));
omega[i].imag(sign*fft_sin(i,size));
}
/*CRT mapping*/
{
int j=0,k=0;
for(int i=0;i<size;i++,j++,k++){
if(j>=n){j=0;} if(k>=m){k=0;}
temp[j+n*k] = array[i];
}
}
for(int i=0;i<size;i++){
array[i] = temp[i];
}
/*===FFT2D===*/
{
dft(array,temp,omega,size,m);
}
/*transpose*/
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
temp[j+i*m] = array[i+j*n];
}
}
for(int i=0;i<size;i++){
array[i] = temp[i];
}
{
dft(array,temp,omega,size,n);
}
/*Good mapping*/
{
int i=0;
for(int j=0;j<n;j++){
for(int k=0;k<m;k++,i++){
temp[(m*j+n*k)%size] = array[i];
}
}
}
for(int i=0;i<size;i++){
array[i] = temp[i];
}
}
-
fft_pfはstd::vector<Complex>型やComplex*型の配列arrayにfftを施す。sizeが要素数で、nがsizeを割り切る数字である。このときnとsizeをnで割った商mは互いに素である必要がある。 -
FFTの行列の列の並び替えは入力の配列の並び替え、行の並び替えは出力の配列の並び替えに対応する。
Prime-Factor型FFTはCooley-Turkey型FFTと違い、twiddle-factorの計算が必要なく、並び替えだけで小さなサイズのFFTに分解できるので、アルゴリズムとしてはシンプルである。この関数は以下の付属関数を使っている。dft(array,temp,omega,size,n)はサイズsize/nのfftを先頭から順番にn回行う関数である。
付属関数コード
void dft(std::vector<Complex> &array){dft(array,array.size());}
template void dft(std::vector<Complex> &array, int size);
template void dft(Complex* &array, int size);
template void dft(
std::vector<Complex> &array,
std::vector<Complex> &temp,
std::vector<Complex> &omega,
int size,
int n
);
template void dft(
Complex* &array,
std::vector<Complex> &temp,
std::vector<Complex> &omega,
int size,
int n
);
template<typename T>
void dft(
T &array,
std::vector<Complex> &temp,
std::vector<Complex> &omega,
int size,
int n
){
int m = size/n;
for(int i=0;i<size;i++){
temp[i] = 0;
}
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
for(int k=0;k<m;k++){
//std::cout << std::floor(size*std::arg(omega[((j*k)%m)*n])/(2*M_PI)) << "\t";
temp[i*m+j] += array[i*m+k]*omega[((j*k)%m)*n];
}
//std::cout << "\n";
}
//std::cout << "\n";
}
for(int i=0;i<size;i++){
array[i] = temp[i];
}
}
template<typename T> void dft(T &array, int size){
std::vector<Complex> temp(size),omega(size);
for(int i=0;i<size;i++){
omega[i].real(fft_cos(i,omega.size()));
omega[i].imag(-fft_sin(i,omega.size()));
}
dft(array,temp,omega,size,1);
}
double fft_cos(int n, int m){
if(n == 0){return 1;}
if(n == m){/*2 Pi*/return 1;}
if(m%n == 0){
if(m/n == 2){/*Pi*/return -1;}
if(m/n == 4){/*Pi/2*/return 0;}
}
if(m%(m-n)==0){
if(m/(m-n)==4){/*3 Pi/2*/return 0;}
}
return cos(2*M_PI*n/m);
}
double fft_sin(int n, int m){
if(n == 0){return 0;}
if(n == m){/*2 Pi*/return 0;}
if(m%n == 0){
if(m/n == 2){/*Pi*/return 0;}
if(m/n == 4){/*Pi/2*/return 1;}
}
if(m%(m-n)==0){
if(m/(m-n)==4){/*3 Pi/2*/return -1;}
}
return sin(2*M_PI*n/m);
}
再帰PFFFT
要素数を素因数分解して、互いに素な因数の数だけ繰り返しPFFFTをかけるプログラムを作る。まず素因数分解のプログラムを作る。
因数分解コード
std::vector<std::vector<int>> factorInteger(int size){
std::vector<int> primes;
int n=1;
for(;;){
int m = size/n;
int p = 2 + (m&1);
for(;p*p<=m;p+=2){
if(m%p==0){
/*m is divisible by p*/
primes.push_back(p);
n *= p;
goto next;
}
}
break;
next:;
}
primes.push_back(size/n);
return tally(primes);
}
std::vector<std::vector<int>> tally(std::vector<int> list){
std::vector<std::vector<int>> res;
for(std::vector<int>::iterator it = list.begin();it!=list.end();it++){
for(std::vector<std::vector<int>>::iterator it2 = res.begin();it2!=res.end();it2++){
if(it2->front() == *it){
it2->back() += 1;
goto loopend;
}
}
res.push_back(std::vector<int>{*it,1});
loopend:;
}
return res;
}
factorIntegerは$n_1^{i_1}n_2^{i_2}n_3^{i_3}...$の形の整数を素因数分解して、{{$n_1,i_1$},{$n_2,i_2$},{$n_3,i_3$},$...$}というネストしたリストを返す。
この関数はまず素因数を見つけていって、primesに格納していく。例えば18だったらprimesは{2,3,3}というリストになる。tallyはこのリストを"集計"して{{2,1},{3,2}}というリストにする。
次にfft_pfの実装を作る。
PFFFTコード
template<typename T> void fft_pf(T &array, int size, int sign){
std::vector<Complex> temp(size),omega(size);
for(int i=0;i<size;i++){
omega[i].real(fft_cos(i,size));
omega[i].imag(sign*fft_sin(i,size));
}
fft_pf(array,temp,omega,size,sign,factorInteger(size),0);
}
template<typename T> void fft_pf(
T &array,
std::vector<Complex> temp,
std::vector<Complex> omega,
int size,
int sign,
std::vector<std::vector<int>> list,
int index
){
//print(list);
if(index==list.size()){return;}
int nn = 1;
for(int i=0;i<index;i++){
nn *= power(list[i][0],list[i][1]);
}
int mm =size/nn;
int n = power(list[index][0],list[index][1]);
int m = mm/n;
/*CRT mapping*/
{
for(int ii=0;ii<nn;ii++){
int j=0,k=0;
for(int i=0;i<mm;i++,j++,k++){
if(j>=n){j=0;} if(k>=m){k=0;}
temp[ii*mm+j+n*k] = array[ii*mm+i];
}
}
}
for(int i=0;i<size;i++){
array[i] = temp[i];
}
/*===FFT2D===*/
{
dft(array,temp,omega,size,size/n);
}
/*transpose*/
for(int ii=0;ii<nn;ii++){
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
temp[ii*mm+j+i*m] = array[ii*mm+i+j*n];
}
}
}
for(int i=0;i<size;i++){
array[i] = temp[i];
}
{
fft_pf(array,temp,omega,size,sign,list,index+1);
}
/*===FFT2D end===*/
/*good mapping*/
{
for(int ii=0;ii<nn;ii++){
int i=0;
for(int j=0;j<n;j++){
for(int k=0;k<m;k++,i++){
temp[ii*mm+(m*j+n*k)%mm] = array[ii*mm+i];
}
}
}
}
for(int i=0;i<size;i++){
array[i] = temp[i];
}
}
int power(int a, int b){
int res = 1;
for(int i=0;i<b;i++){res *= a;}
return res;
}
このプログラムの再帰は下図のイメージのようになる。この関数がやることは、「サイズmmのfftをnn回やること」になっている。なので一段PFFFTで行った作業をnn回ループさせていて、サイズmの代わりにmmになっている。
mm$は$nとそれと互いに素なmの積になっていて、またnはそれ以上互いに素な数の積に分解できない数(素数のべき乗)である。Prime-Factorのアルゴリズムを適用して、サイズmmのfftをサイズnのfft(size/n回)と、サイズm=mm/nのfft(size/m=nn*n回)に分解する。nはもう分解できない数なので、サイズnのfftはdftで計算する。最後にサイズmm/nのfftをnn*n回やればいい状態になるので、次の再帰にわたす。次の再帰ではnn=n*nn,mm=mm/nとなる。

素数のべき乗のdftをCooley-Turkey型のfftによって置き換えた完全版コードを以下にのせる。hardcordの部分は任意要素数の高速フーリエ変換にある。
完全版コードとその他
# ifndef FFT_H
# define FFT_H
# include <iostream>
# include <complex>
# include <vector>
# include <list>
# include <fft_hardcord.h>
# define FFT_PRIME_THRESHOLD 256
using Complex = std::complex<double>;
template<typename T> void fft(T &array, int size);
template<typename T> void ifft(T &array, int size);
template<typename T> void fft2d(T &array, int row, int column);
template<typename T> void ifft2d(T &array, int row, int column);
template<typename T> void dft(T &array, int size);
template<typename T> void idft(T &array, int size);
void fft(std::vector<Complex> &array);
void ifft(std::vector<Complex> &array);
void dft(std::vector<Complex> &array);
void idft(std::vector<Complex> &array);
/*internal functions*/
template<typename T>
void dft(
T &array,
std::vector<Complex> &temp,
std::vector<Complex> &omega,
int size,
int n
);
template<typename T> void fft2(
T &array,
std::vector<Complex> &temp,
std::vector<Complex> &omega,
int size
);
template<typename T> void fft_prime(T &array,int size,int n,int sign);
template<typename T> void fft(T &array, int size, int sign);
template<typename T> void fft2d(T &array, int row, int column, int sign);
double fft_cos(int n, int m);
double fft_sin(int n, int m);
int primePrimitiveRoot(int p);
int powerMod(int a, int b, int m);
int eulerPhi(int n);
int primitiveRoot(int n);
int primitiveRoot(int n, int phi);
std::vector<std::vector<int>> factorInteger(int size);
std::vector<std::vector<int>> tally(std::vector<int> list);
void print(std::vector<std::vector<int>> &list);
void fft_pf(std::vector<Complex> &array);
template<typename T> void fft_pf(T &array, int size);
template<typename T> void fft_pf(T &array, int size, int sign);
template<typename T> void fft_pf(
T &array,
std::vector<Complex> temp,
std::vector<Complex> omega,
int size,
int sign,
std::vector<std::vector<int>> list,
int index
);
void fft_rec(std::vector<Complex> &array);
template<typename T> void fft_rec(T &array, int size);
template<typename T> void fft_rec(T &array, int size, int sign);
template<typename T> void fft_rec(
T &array,
std::vector<Complex> &temp,
std::vector<Complex> &omega,
int size,
int n,
int sign
);
# endif
# include <fft.h>
# include <iostream>
void dft(std::vector<Complex> &array){dft(array,array.size());}
template void dft(std::vector<Complex> &array, int size);
template void dft(Complex* &array, int size);
template void dft(
std::vector<Complex> &array,
std::vector<Complex> &temp,
std::vector<Complex> &omega,
int size,
int n
);
template void dft(
Complex* &array,
std::vector<Complex> &temp,
std::vector<Complex> &omega,
int size,
int n
);
template<typename T>
void dft(
T &array,
std::vector<Complex> &temp,
std::vector<Complex> &omega,
int size,
int n
){
int m = size/n;
for(int i=0;i<size;i++){
temp[i] = 0;
}
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
for(int k=0;k<m;k++){
//std::cout << std::floor(size*std::arg(omega[((j*k)%m)*n])/(2*M_PI)) << "\t";
temp[i*m+j] += array[i*m+k]*omega[((j*k)%m)*n];
}
//std::cout << "\n";
}
//std::cout << "\n";
}
for(int i=0;i<size;i++){
array[i] = temp[i];
}
}
template<typename T> void dft(T &array, int size){
std::vector<Complex> temp(size),omega(size);
for(int i=0;i<size;i++){
omega[i].real(fft_cos(i,omega.size()));
omega[i].imag(-fft_sin(i,omega.size()));
}
dft(array,temp,omega,size,1);
}
template<typename T> void idft(T &array, int size){
std::vector<Complex> temp(size),omega(size);
for(int i=0;i<size;i++){
omega[i].real(fft_cos(i,omega.size()));
omega[i].imag(fft_sin(i,omega.size()));
}
dft(array,temp,omega,size,-1);
for(int i=0;i<size;i++){array[i] /= size;}
}
template<typename T> void fft2(
T &array,
std::vector<Complex> &temp,
std::vector<Complex> &omega,
int size
){
int n=1;
for(;n<size;n <<= 1){
int m = size/n;
int q = m>>1;
/*permutation*/
for(int i=0;i<n;i++){
for(int k=0;k<q;k++){
temp[i*m+k] = array[i*m+2*k];
temp[i*m+q+k] = array[i*m+2*k+1];
}
}
for(int i=0;i<size;i++){array[i] = temp[i];}
}
for(;n>1;n >>= 1){
int m = size/n;
int q = n>>1;
int r = size/q;
/*adding up with twiddle factors*/
for(int i=0;i<size;i++){temp[i] = 0;}
for(int i=0;i<q;i++){
for(int k=0;k<m;k++){
temp[2*m*i+k] += array[2*m*i+k];
temp[2*m*i+m+k] += array[2*m*i+k];
temp[2*m*i+k] += array[2*m*i+m+k]*omega[(k%r)*q];
temp[2*m*i+m+k] += array[2*m*i+m+k]*omega[((m+k)%r)*q];
}
}
for(int i=0;i<size;i++){array[i] = temp[i];}
}
}
void fft2(
std::vector<Complex> &array,
std::vector<Complex> &temp,
std::vector<Complex> &omega
){
fft2(array,temp,omega,array.size());
}
template<typename T> void fft_prime(T &array,int size,int n,int sign){
int p = size/n;
int len=p-1;
bool power2=true;
int i=0;
for(;len>1;len>>=1,i++){
if(len & 1){power2=false;}
}
len = power2 ? p-1 : (1<<(i+2));
/*
std::cout << "p-1 : " << p-1 << "\n";
std::cout << "len : " << len << "\n";
*/
int pad = len - (p-1);
int g = primePrimitiveRoot(p);
int ig = powerMod(g,p-2,p);
std::vector<Complex> data(len),temp(len),omega(len),omega2(len);
for(int i=0;i<len;i++){
omega[i].real(fft_cos(i,len));
omega[i].imag(-fft_sin(i,len));
omega2[i].real(fft_cos(powerMod(ig,i%(p-1),p),p));
omega2[i].imag(sign*fft_sin(powerMod(ig,i%(p-1),p),p));
}
fft2(omega2,temp,omega);
for(int i=0;i<n;i++){
data[0] = array[i*p+1];
for(int j=1;j<len;j++){
if(j <= pad){
data[j] = 0;
}else{
data[j] = array[i*p+powerMod(g,j-pad,p)];
}
}
/*===Convolution theorem===*/
fft2(data,temp,omega);
for(int j=0;j<len;j++){temp[j] = data[j]*omega2[j];}
for(int j=0;j<len;j++){
data[j] = temp[j];
omega[j].imag(-omega[j].imag());
}
fft2(data,temp,omega);
/*add array[i*p] term*/
for(int j=0;j<len;j++){
data[j].real(data[j].real()/len + array[i*p].real());
data[j].imag(data[j].imag()/len + array[i*p].imag());
//data[j] = data[j]/(Complex(len)) + array[i*p];
//omega[j].imag(-omega[j].imag());
}
/*===Convolution theorem end===*/
/*DC term*/
temp[0]=0;
for(int j=0;j<p;j++){temp[0] += array[i*p+j];}
array[i*p] = temp[0];
/*non-DC term*/
for(int j=0;j<p-1;j++){array[i*p+powerMod(ig,j,p)] = data[j];}
}
}
template<typename T> void fft(
T &array,
int size,
int sign
){
std::vector<Complex> temp(size),omega(size);
for(int i=0;i<size;i++){
omega[i].real(fft_cos(i,size));
omega[i].imag(sign*fft_sin(i,size));
}
int primes[32];
int np=0;
int n=1;
for(;;){
int m = size/n;
int p = 2 + (m&1);
for(;p*p<=m;p+=2){
if(m%p==0){
/*m is divisible by p*/
int q = m/p;
/*permutation*/
for(int i=0;i<n;i++){
for(int j=0;j<p;j++){
for(int k=0;k<q;k++){
temp[i*m+q*j+k] = array[i*m+p*k+j];
}
}
}
for(int i=0;i<size;i++){
array[i] = temp[i];
}
primes[np++]=p;
n *= p;
if(q <= FFT_HARDCORD_SIZE){break;}
goto next;
}
}
break;
next:;
}
/*bottom of recursion*/
/*perform dft on n sub-arrays*/
{
if(size/n <= FFT_HARDCORD_SIZE){
fft_hardcord(array,size,n,sign);
}else if(size/n <= FFT_PRIME_THRESHOLD){
dft(array,temp,omega,size,n);
}else{
fft_prime(array,size,n,sign);
}
}
/*sum up with twiddle factors*/
for(int h=np-1;h>=0;h--){
int m = size/n;
int p = primes[h];
int q = n/p;
int r = size/q;
for(int i=0;i<size;i++){temp[i] = 0;}
for(int i=0;i<q;i++){
for(int j=0;j<p;j++){
for(int k=0;k<m;k++){
for(int l=0;l<p;l++){
temp[i*p*m+(j*m+k)] += array[i*p*m+(l*m+k)]*omega[(l*(j*m+k)%r)*q];
}
}
}
}
for(int i=0;i<size;i++){array[i] = temp[i];}
n = q;
}
}
void fft(std::vector<Complex> &array){fft(array,array.size());}
template void fft(std::vector<Complex> &array, int size, int sign);
template void fft(std::vector<Complex> &array, int size);
template void fft(Complex* &array, int size, int sign);
template void fft(Complex* &array, int size);
template<typename T> void fft(T &array, int size){fft(array,size,-1);}
template<typename T> void ifft(T &array, int size){
fft(array,size,1);
for(int i=0;i<size;i++){array[i] /= size;}
}
template<typename T> void fft2d(T &array, int row, int column, int sign){
int size = row*column;
std::vector<Complex> temp(size),omega(size);
for(int i=0;i<size;i++){
omega[i].real(fft_cos(i,size));
omega[i].imag(sign*fft_sin(i,size));
}
int primes[32];
int np=0;
int n=row;
for(;;){
int m = size/n;
int p = 2 + (m&1);
for(;p*p<=m;p+=2){
if(m%p==0){
/*m is divisible by p*/
int q = m/p;
/*permutation*/
for(int i=0;i<n;i++){
for(int j=0;j<p;j++){
for(int k=0;k<q;k++){
temp[i*m+q*j+k] = array[i*m+p*k+j];
}
}
}
for(int i=0;i<size;i++){
array[i] = temp[i];
}
primes[np++]=p;
n *= p;
if(q <= FFT_HARDCORD_SIZE){break;}
goto next1;
}
}
break;
next1:;
}
/*bottom of recursion*/
/*perform dft on n sub-arrays*/
{
if(size/n <= FFT_HARDCORD_SIZE){
fft_hardcord(array,size,n,sign);
}else if(size/n <= FFT_PRIME_THRESHOLD){
dft(array,temp,omega,size,n);
}else{
fft_prime(array,size,n,sign);
}
}
/*integrate array elements multiplied by twiddle factors*/
for(int h=np-1;h>=0;h--){
int m = size/n;
int p = primes[h];
int q = n/p;
int r = size/q;
for(int i=0;i<size;i++){temp[i] = 0;}
for(int i=0;i<q;i++){
for(int j=0;j<p;j++){
for(int k=0;k<m;k++){
for(int l=0;l<p;l++){
temp[i*p*m+(j*m+k)] += array[i*p*m+(l*m+k)]*omega[(l*(j*m+k)%r)*q];
}
}
}
}
for(int i=0;i<size;i++){array[i] = temp[i];}
n = q;
}
/*transpose*/
for(int i=0;i<row;i++){
for(int j=0;j<column;j++){
temp[j*row+i] = array[i*column+j];
}
}
for(int i=0;i<size;i++){
array[i] = temp[i];
}
np=0;
n=column;
for(;;){
int m = size/n;
int p = 2 + (m&1);
for(;p*p<=m;p+=2){
if(m%p==0){
/*m is divisible by p*/
int q = m/p;
/*permutation*/
for(int i=0;i<n;i++){
for(int j=0;j<p;j++){
for(int k=0;k<q;k++){
temp[i*m+q*j+k] = array[i*m+p*k+j];
}
}
}
for(int i=0;i<size;i++){
array[i] = temp[i];
}
primes[np++]=p;
n *= p;
if(q <= FFT_HARDCORD_SIZE){break;}
goto next2;
}
}
break;
next2:;
}
/*bottom of recursion*/
/*perform dft on n sub-arrays*/
{
if(size/n <= FFT_HARDCORD_SIZE){
fft_hardcord(array,size,n,sign);
}else if(size/n <= FFT_PRIME_THRESHOLD){
dft(array,temp,omega,size,n);
}else{
fft_prime(array,size,n,sign);
}
}
/*sum up with twiddle factors*/
for(int h=np-1;h>=0;h--){
int m = size/n;
int p = primes[h];
int q = n/p;
int r = size/q;
for(int i=0;i<size;i++){temp[i] = 0;}
for(int i=0;i<q;i++){
for(int j=0;j<p;j++){
for(int k=0;k<m;k++){
for(int l=0;l<p;l++){
temp[i*p*m+(j*m+k)] += array[i*p*m+(l*m+k)]*omega[(l*(j*m+k)%r)*q];
}
}
}
}
for(int i=0;i<size;i++){array[i] = temp[i];}
n = q;
}
/*transpose*/
for(int i=0;i<column;i++){
for(int j=0;j<row;j++){
temp[j*column+i] = array[i*row+j];
}
}
for(int i=0;i<size;i++){
array[i] = temp[i];
}
}
template<typename T> void fft2d(T &array, int row, int column){fft2d(array,row,column,-1);}
template<typename T> void ifft2d(T &array, int row, int column){
fft2d(array,row,column,1);
for(int i=0;i<row*column;i++){array[i] /= (row*column);}
}
void ifft(std::vector<Complex> &array){ifft(array,array.size());}
void idft(std::vector<Complex> &array){idft(array,array.size());}
double fft_cos(int n, int m){
if(n == 0){return 1;}
if(n == m){/*2 Pi*/return 1;}
if(m%n == 0){
if(m/n == 2){/*Pi*/return -1;}
if(m/n == 4){/*Pi/2*/return 0;}
}
if(m%(m-n)==0){
if(m/(m-n)==4){/*3 Pi/2*/return 0;}
}
return cos(2*M_PI*n/m);
}
double fft_sin(int n, int m){
if(n == 0){return 0;}
if(n == m){/*2 Pi*/return 0;}
if(m%n == 0){
if(m/n == 2){/*Pi*/return 0;}
if(m/n == 4){/*Pi/2*/return 1;}
}
if(m%(m-n)==0){
if(m/(m-n)==4){/*3 Pi/2*/return -1;}
}
return sin(2*M_PI*n/m);
}
int eulerPhi(int n){
int res = n;
for(int i=2;i*i<=n;i++){
if(n%i==0){
while(n%i==0){n/=i;}
res -= res/i;
}
}
if(n>1){
res -= res/n;
}
return res;
}
int primitiveRoot(int n){
return primitiveRoot(n,eulerPhi(n));
}
int primitiveRoot(int n, int phi){
int i,t;
std::vector<int> list;
for(i=2,t=phi;i*i<=t;i++){
if(t % i == 0){
list.push_back(i);
do{
t/=i;
}while(t%i==0);
}
}
for(std::vector<int>::iterator it = list.begin();it != list.end();it++){
*it = phi / (*it);
}
for(i=2;i<=phi;i++){
for(std::vector<int>::iterator it = list.begin();it != list.end();it++){
if(powerMod(i,*it,phi)==1){
goto loopend;
}
}
break;
loopend:;
}
return i;
}
int primePrimitiveRoot(int p){
int i,t;
std::vector<int> list;
for(i=2,t=p-1;i*i<=t;i++){
if(t % i == 0){
list.push_back(i);
do{
t/=i;
}while(t%i==0);
}
}
for(std::vector<int>::iterator it = list.begin();it != list.end();it++){
*it = (p-1) / (*it);
}
for(i=2;i<=p-1;i++){
for(std::vector<int>::iterator it = list.begin();it != list.end();it++){
if(powerMod(i,*it,p)==1){
goto loopend;
}
}
break;
loopend:;
}
return i;
}
int powerMod(int a, int b, int m){
int i;
for(i=1;b;b>>=1){
if(b & 1){
i = (i*a)%m;
}
a = (a*a)%m;
}
return i;
}
template void ifft(std::vector<Complex> &array, int size);
template void fft2d(std::vector<Complex> &array, int row, int column);
template void ifft2d(std::vector<Complex> &array, int row, int column);
template void idft(std::vector<Complex> &array, int size);
template void fft2(
std::vector<Complex> &array,
std::vector<Complex> &temp,
std::vector<Complex> &omega,
int size
);
template void fft_prime(std::vector<Complex> &array,int size,int n,int sign);
template void fft2d(std::vector<Complex> &array, int row, int column, int sign);
template void ifft(Complex* &array, int size);
template void fft2d(Complex* &array, int row, int column);
template void ifft2d(Complex* &array, int row, int column);
template void idft(Complex* &array, int size);
template void fft2(
Complex* &array,
std::vector<Complex> &temp,
std::vector<Complex> &omega,
int size
);
template void fft_prime(Complex* &array,int size,int n,int sign);
template void fft2d(Complex* &array, int row, int column, int sign);
std::vector<std::vector<int>> factorInteger(int size){
std::vector<int> primes;
int n=1;
for(;;){
int m = size/n;
int p = 2 + (m&1);
for(;p*p<=m;p+=2){
if(m%p==0){
/*m is divisible by p*/
primes.push_back(p);
n *= p;
goto next;
}
}
break;
next:;
}
primes.push_back(size/n);
return tally(primes);
}
std::vector<std::vector<int>> tally(std::vector<int> list){
std::vector<std::vector<int>> res;
for(std::vector<int>::iterator it = list.begin();it!=list.end();it++){
for(std::vector<std::vector<int>>::iterator it2 = res.begin();it2!=res.end();it2++){
if(it2->front() == *it){
it2->back() += 1;
goto loopend;
}
}
res.push_back(std::vector<int>{*it,1});
loopend:;
}
return res;
}
void print(std::vector<std::vector<int>> &list){
std::cout << "{";
for(std::vector<std::vector<int>>::iterator it = list.begin();it!=list.end();it++){
std::cout << "{";
for(std::vector<int>::iterator it2 = it->begin();it2!=it->end();it2++){
std::cout << *it2;
if(std::next(it2) != it->end()){std::cout << ",";}
}
std::cout << "}";
if(std::next(it) != list.end()){std::cout << ",";}
}
std::cout << "}\n";
}
int power(int a, int b){
int res = 1;
for(int i=0;i<b;i++){res *= a;}
return res;
}
void fft_pf(std::vector<Complex> &array){fft_pf(array,array.size());}
template<typename T> void fft_pf(T &array, int size){fft_pf(array,size,-1);}
template void fft_pf(std::vector<Complex> &array, int size);
template void fft_pf(Complex* &array, int size);
template void fft_pf(std::vector<Complex> &array, int size, int sign);
template void fft_pf(Complex* &array, int size, int sign);
template<typename T> void fft_pf(T &array, int size, int sign){
std::vector<Complex> temp(size),omega(size);
for(int i=0;i<size;i++){
omega[i].real(fft_cos(i,size));
omega[i].imag(sign*fft_sin(i,size));
}
fft_pf(array,temp,omega,size,sign,factorInteger(size),0);
}
template<typename T> void fft_pf(
T &array,
std::vector<Complex> temp,
std::vector<Complex> omega,
int size,
int sign,
std::vector<std::vector<int>> list,
int index
){
//print(list);
if(index==list.size()){return;}
int nn = 1;
for(int i=0;i<index;i++){
nn *= power(list[i][0],list[i][1]);
}
int mm =size/nn;
int n = power(list[index][0],list[index][1]);
int m = mm/n;
/*CRT mapping*/
{
for(int ii=0;ii<nn;ii++){
int j=0,k=0;
for(int i=0;i<mm;i++,j++,k++){
if(j>=n){j=0;} if(k>=m){k=0;}
temp[ii*mm+j+n*k] = array[ii*mm+i];
}
}
}
for(int i=0;i<size;i++){
array[i] = temp[i];
}
/*===FFT2D===*/
{
//dft(array,temp,omega,size,size/n);
fft_rec(array,temp,omega,size,size/n,sign);
}
/*transpose*/
for(int ii=0;ii<nn;ii++){
for(int i=0;i<n;i++){
for(int j=0;j<m;j++){
temp[ii*mm+j+i*m] = array[ii*mm+i+j*n];
}
}
}
for(int i=0;i<size;i++){
array[i] = temp[i];
}
{
fft_pf(array,temp,omega,size,sign,list,index+1);
}
/*===FFT2D end===*/
/*good mapping*/
{
for(int ii=0;ii<nn;ii++){
int i=0;
for(int j=0;j<n;j++){
for(int k=0;k<m;k++,i++){
temp[ii*mm+(m*j+n*k)%mm] = array[ii*mm+i];
}
}
}
}
for(int i=0;i<size;i++){
array[i] = temp[i];
}
}
void fft_rec(std::vector<Complex> &array){fft_rec(array,array.size());}
template<typename T> void fft_rec(T &array, int size){fft_rec(array,size,-1);}
template void fft_rec(std::vector<Complex> &array, int size);
template void fft_rec(Complex* &array, int size);
template void fft_rec(std::vector<Complex> &array, int size, int sign);
template void fft_rec(Complex* &array, int size, int sign);
template void fft_rec(std::vector<Complex> &array, int size, int sign);
template void fft_rec(Complex* &array, int size, int sign);
template void fft_rec(
std::vector<Complex> &array,
std::vector<Complex> &temp,
std::vector<Complex> &omega,
int size,
int n,
int sign
);
template void fft_rec(
Complex* &array,
std::vector<Complex> &temp,
std::vector<Complex> &omega,
int size,
int n,
int sign
);
template<typename T> void fft_rec(T &array, int size, int sign){
std::vector<Complex> temp(size),omega(size);
for(int i=0;i<size;i++){
omega[i].real(fft_cos(i,size));
omega[i].imag(sign*fft_sin(i,size));
}
fft_rec(array,temp,omega,size,1,sign);
}
template<typename T> void fft_rec(
T &array,
std::vector<Complex> &temp,
std::vector<Complex> &omega,
int size,
int n,
int sign
){
int m = size/n;
int p = 2 + (m&1);
for(;p*p<=m;p+=2){
if(m%p==0){
/*m is divisible by p*/
int q = m/p;
/*permutation*/
for(int i=0;i<n;i++){
for(int j=0;j<p;j++){
for(int k=0;k<q;k++){
temp[i*m+q*j+k] = array[i*m+p*k+j];
}
}
}
for(int i=0;i<size;i++){
array[i] = temp[i];
}
n *= p;
m /= p;
fft_rec(array,temp,omega,size,n,sign);
q = n/p;
int r = size/q;
for(int i=0;i<size;i++){temp[i] = 0;}
for(int i=0;i<q;i++){
for(int j=0;j<p;j++){
for(int k=0;k<m;k++){
for(int l=0;l<p;l++){
temp[i*p*m+(j*m+k)] += array[i*p*m+(l*m+k)]*omega[(l*(j*m+k)%r)*q];
}
}
}
}
for(int i=0;i<size;i++){array[i] = temp[i];}
return;
}
}
/*bottom of recursion*/
/*perform dft on n sub-arrays*/
if(size/n <= FFT_HARDCORD_SIZE){
fft_hardcord(array,size,n,sign);
}else if(size/n <= FFT_PRIME_THRESHOLD){
dft(array,temp,omega,size,n);
}else{
fft_prime(array,size,n,sign);
}
}
動作テストコードとその他
# include <fft.h>
# include <Array2D.h>
# include <vector>
int main(int argc, char *argv[]){
Array2D a,b;
if(argc > 1){
a.read(argv[1]);
b.set(a.rows,2*a.columns);
if(a.columns >= 2){
std::vector<Complex> array(a.rows);
for(int i=0;i<a.rows;i++){
array[i].real(a[i][0]);
array[i].imag(a[i][1]);
}
fft(array);
for(int i=0;i<b.rows;i++){
b[i][0] = array[i].real();
b[i][1] = array[i].imag();
}
for(int i=0;i<a.rows;i++){
array[i].real(a[i][0]);
array[i].imag(a[i][1]);
}
fft_pf(array);
for(int i=0;i<b.rows;i++){
b[i][2] = array[i].real();
b[i][3] = array[i].imag();
}
std::streambuf *buf;
if(argc > 2){
buf = std::ofstream(argv[2]).rdbuf();
}else{
buf = std::cout.rdbuf();
}
std::ostream os(buf);
b.print(os);
}
}else{
std::cout << "usage : " << argv[0] << " [input file] [output file]\n";
}
}
# ifndef ARRAY2D_H
# define ARRAY2D_H
# include <iostream>
# include <fstream>
# include <list>
# include <string>
# include <string.h>
# include <sys/stat.h>
struct Array2D{
struct ReadOptions{
enum {automatic=-1};
int rows;
int columns;
int rowOffset;
int columnOffset;
std::list<std::string> lineSeparators;
std::list<std::string> fieldSeparators;
bool repeatedSeparators;
bool ignoreEmptyLines;
ReadOptions();
};
enum precision{p_double,p_float};
double **data;
int rows;
int columns;
Array2D();
Array2D(int,int);
Array2D(const Array2D&);
Array2D(Array2D&&);
Array2D& operator=(const Array2D &array);
Array2D& operator=(Array2D &&array);
virtual ~Array2D();
void set(int rows, int columns);
void clear();
void print();
void print(const char *fileName);
void print(std::ostream &os);
void exportBMAT(const char *fileName,precision p);
Array2D& read(const char *fileName, ReadOptions &options);
Array2D& read(const char *fileName);
double interpolate(double x);
double min();
double minRow(int row);
double minColumn(int column);
double*& operator[] (const int index);
private:
struct Matcher{
Matcher(std::list<std::string>&);
~Matcher();
void clear();
int count(char *str,bool repeatedSeparators);
char *replace(char *p, char c);
char *match(char *p);
char *tokenize(char **str,bool repeatedSeparators);
void tokenize(char *str,std::list<char*> &list,bool repeatedSeparators);
size_t size;
const char **list[2];
};
};
# endif
# include <Array2D.h>
Array2D::Array2D(){
this->rows=0;
this->columns=0;
this->data=nullptr;
}
Array2D::Array2D(int rows, int columns){
this->set(rows,columns);
}
Array2D::Array2D(const Array2D &array){
this->set(array.rows,array.columns);
for(int i=0;i<rows;i++){
for(int j=0;j<columns;j++){
data[i][j] = array.data[i][j];
}
}
}
Array2D::Array2D(Array2D &&array){
rows = array.rows;
columns = array.columns;
data = array.data;
}
Array2D& Array2D::operator=(const Array2D &array){
Array2D tmp(array);
*this = std::move(tmp);
tmp.data=nullptr;
return *this;
}
Array2D& Array2D::operator=(Array2D &&array){
if(this==&array){
return *this;
}
rows = array.rows;
columns = array.columns;
data = array.data;
return *this;
}
Array2D::~Array2D(){
this->clear();
}
void Array2D::set(int rows, int columns){
this->rows = rows;
this->columns = columns;
data = new double*[rows];
data[0] = new double[rows*columns];
for(int i=1;i<rows;i++){
data[i] = &(data[0][i*columns]);
}
}
void Array2D::clear(){
if(data){
delete[] data[0];
delete[] data;
data = nullptr;
}
}
void Array2D::print(){
std::ostream os(std::cout.rdbuf());
print(os);
}
void Array2D::print(const char *fileName){
std::ostream os(std::ofstream(fileName).rdbuf());
print(os);
}
void Array2D::print(std::ostream &os){
os.precision(17);
for(int i=0;i<rows;i++){
for(int j=0;j<columns;j++){
os << std::fixed << data[i][j] << "\t";
}
os << "\n";
}
}
void Array2D::exportBMAT(const char *fileName, Array2D::precision p){
FILE *fp = fopen(fileName,"wb");
if(!fp){std::cout << "exportBMAT : unable to open file " << fileName << "\n"; return;}
fwrite(&p,sizeof(precision),1,fp);
fwrite(&rows,sizeof(int),1,fp);
fwrite(&columns,sizeof(int),1,fp);
int w1;
float *f;
switch(p){
case p_double:
if((w1=fwrite(data[0],sizeof(double),rows*columns,fp))!=rows*columns){
std::cout << "exportBMAT : tried to write " <<
rows*columns*sizeof(double) << " bytes, but " <<
w1*sizeof(double) << " bytes were written\n";
}
break;
case p_float:
f = new float[rows*columns];
for(int i=0;i<rows;i++){
for(int j=0;j<columns;j++){
f[i*columns+j] = data[i][j];
}
}
if((w1=fwrite(f,sizeof(float),rows*columns,fp))!=rows*columns){
std::cout << "exportBMAT : tried to write " <<
rows*columns*sizeof(float) << " bytes, but " <<
w1*sizeof(float) << " bytes were written\n";
}
delete[] f;
break;
}
fclose(fp);
}
Array2D::ReadOptions::ReadOptions() :
lineSeparators({"\r\n","\n","\r"}),
fieldSeparators({"\t"," "})
{
rows = ReadOptions::automatic;
columns = ReadOptions::automatic;
rowOffset = 0;
columnOffset = 0;
repeatedSeparators = true;
ignoreEmptyLines = false;
}
Array2D& Array2D::read(const char *fileName, ReadOptions &options){
struct stat st;
size_t size;
if(stat(fileName,&st)==0){size = st.st_size+1;}
FILE *fp = fopen(fileName,"r");
if(!fp){
std::cout << "unable to open " << fileName << "\n";
return *this;
}
setbuf(fp,NULL);
char *buffer = new char[size];
fread(buffer,1,size,fp);
buffer[size-1] = '\0';
fclose(fp);
Matcher lineMatcher(options.lineSeparators);
Matcher fieldMatcher(options.fieldSeparators);
std::list<char*> listRow;
lineMatcher.tokenize(buffer,listRow,options.repeatedSeparators);
for(std::list<char*>::iterator it=listRow.begin();it!=listRow.end();it++){
if(fieldMatcher.count(*it,options.repeatedSeparators)==0){
*it = NULL;
}
}
listRow.remove(NULL);
rows = listRow.size();
int rowOffset = options.rowOffset < 0 ?
rows + options.rowOffset :
options.rowOffset;
if(options.rows == ReadOptions::automatic){
if(rows < rowOffset){
std::cout << "row offset " << rowOffset << "exceeds the row size " << rows << "\n";
return *this;
}
rows = rows - rowOffset;
}else{
if(rows < options.rows + rowOffset){
std::cout << "row size "<< options.rows <<
" + rowOffset " << rowOffset << " exceeds the row size of input " << rows << "\n";
return *this;
}
rows = options.rows;
}
std::list<char*>::iterator it = listRow.begin();
for(int i=0;it != listRow.end() && i<rowOffset;it++,i++){}
columns = fieldMatcher.count(*it,options.repeatedSeparators);
int columnOffset = options.columnOffset < 0 ?
columns + options.columnOffset :
options.columnOffset;
if(options.columns == ReadOptions::automatic){
if(columns < columnOffset){
std::cout << "column offset " << columnOffset << "exceeds the column size " << rows << "\n";
return *this;
}
columns = columns - columnOffset;
}else{
if(columns < options.columns + columnOffset){
std::cout << "column size "<< options.columns <<
" + columnOffset " << columnOffset << " exceeds the column size of input " << columns << "\n";
return *this;
}
columns = options.columns;
}
//std::cout << "rows : " << rows << std::endl;
//std::cout << "columns : " << columns << "\n";
this->set(rows,columns);
for(int i=0;it!=listRow.end() && i<rows;it++,i++){
char *p = *it;
for(int j=0;j<columnOffset;j++){
fieldMatcher.clear();
fieldMatcher.tokenize(&p,options.repeatedSeparators);
}
for(int j=0;j<columns;j++){
fieldMatcher.clear();
//fieldMatcher.tokenize(&p,options.repeatedSeparators);
data[i][j] = atof(fieldMatcher.tokenize(&p,options.repeatedSeparators));
}
}
return *this;
}
Array2D& Array2D::read(const char *fileName){
ReadOptions options;
return read(fileName,options);
}
double Array2D::interpolate(double x){
// assumes x data are in 0th column, y data are in 1th column;
// assumes x data are sorted in increasing order.
if(x < data[0][0]){
return (x - data[0][0])*(data[1][1]-data[0][1])/(data[1][0]-data[0][0]) + data[0][1];
}
if(x > data[rows-1][0]){
return (x - data[rows-1][0])*(data[rows-1][1]-data[rows-2][1])/(data[rows-1][0]-data[rows-2][0]) + data[rows-1][1];
}
int i=0;
for(;i<rows && x >= data[i][0];i++){}
return (x-data[i][0])*(data[i][1]-data[i-1][1])/(data[i][0]-data[i-1][0]) + data[i][1];
}
double*& Array2D::operator[] (const int index){
return data[index];
}
double Array2D::min(){
double min = data[0][0];
for(int i=0;i<rows*columns;i++){
if(min > data[0][i]){min = data[0][i];}
}
return min;
}
double Array2D::minRow(int row){
double min = data[row][0];
for(int i=0;i<columns;i++){
if(min > data[row][i]){min = data[row][i];}
}
return min;
}
double Array2D::minColumn(int column){
double min = data[0][column];
for(int i=0;i<rows;i++){
if(min > data[i][column]){min = data[i][column];}
}
return min;
}
Array2D::Matcher::Matcher(std::list<std::string> &list){
size = list.size();
this->list[0] = new const char*[size];
this->list[1] = new const char*[size];
int i=0;
for(std::list<std::string>::iterator it=list.begin();
it != list.end();
it++,i++
){
this->list[0][i] = this->list[1][i] = it->c_str();
}
}
Array2D::Matcher::~Matcher(){
delete[] list[0];
delete[] list[1];
}
void Array2D::Matcher::clear(){
for(int i=0;i<size;i++){list[1][i] = list[0][i];}
}
char *Array2D::Matcher::match(char *p){
for(int i=0;i<size;i++){
if(*list[1][i]==*p){
list[1][i]++;
if(*list[1][i]=='\0'){
for(int j=0;j<size;j++){list[1][j] = list[0][j];}
int len = strlen(list[0][i]);
return p-len+1;
}
}else{
list[1][i] = list[0][i];
}
}
return NULL;
}
char *Array2D::Matcher::replace(char *p, char c){
for(int i=0;i<size;i++){
if(*list[1][i]==*p){
list[1][i]++;
if(*list[1][i]=='\0'){
for(int j=0;j<size;j++){list[1][j] = list[0][j];}
int len = strlen(list[0][i]);
char *pp = p;
for(;p-pp < len;pp--){*pp=c;}
return pp+1;
}
}else{
list[1][i] = list[0][i];
}
}
return NULL;
}
int Array2D::Matcher::count(char *str,bool repeatedSeparators){
int counter=0;
char *p,*ps,*pe,*pm,*tail;
tail = pe = strchr(str,'\0');
for(ps=p=str;*p;p++){
pm = this->match(p);
if(pm){
pe = pm;
if(!repeatedSeparators || ps!=pe){++counter;}
ps = p+1;
}
}
if(*ps && ps < tail){counter++;}
return counter;
}
char *Array2D::Matcher::tokenize(char **str,bool repeatedSeparators){
char *p,*ps,*pe,*pm;
pe = strchr(*str,'\0');
for(ps=p=*str;*p;p++){
pm = this->replace(p,'\0');
if(pm){
pe = pm;
if(!repeatedSeparators || ps!=pe){
*str = p+1; return ps;
}
ps = p+1;
}
}
return ps;
}
void Array2D::Matcher::tokenize(char *str, std::list<char*> &list, bool repeatedSeparators){
char *p,*ps,*pe,*pm,*tail;
tail = pe = strchr(str,'\0');
for(ps=p=str;*p;p++){
pm = this->replace(p,'\0');
if(pm){
pe = pm;
if(!repeatedSeparators || ps != pe){
list.push_back(ps);
}
ps = p+1;
}
}
if(*ps && ps < tail){list.push_back(ps);}
}
素数のべき乗のサイズのFFT
Prime-Factor型は互いに素な数の分解ができるので、あとは素数のべき乗のサイズのFFTができればよくなる。素数のべき乗サイズに特化したものをRaderのアルゴリズムを一般化して考えてみた。
下図はサイズ27のDFT行列をRaderのアルゴリズムを一般化した方法で並び替えたものである。結果的に、サイズ27のDFTが、サイズ18、サイズ6、サイズ2の巡回畳み込みに分解される。ただこれを実装しようとすると、まずRaderのアルゴリズムをin-placeにしないと非効率だし、計算の順番をよく考えないと一時保存用の配列をたくさん生成することになる。難しそうなので断念した。
ベンチマーク
- 赤 : FFT
- 青 : 通常のDFT
- 緑 : PFFFT
- Prime-Factor型はCooley-Turkey型と比べ速度はあまり変わらなかった。
感想
- 任意要素数の高速フーリエ変換と今回のPrime-Factor型アルゴリズムを勉強してみてわかったのは、FFTの種々のアルゴリズムはDFT行列に対してルービックキューブのような並び替えゲームをしていること。そしてその本質には群論があるということである。
- Radorのアルゴリズムで並び替えで巡回畳み込みにするところまでは可視化できたが、畳み込みがFFTでどうして早くなるかというとこまでは可視化できていないのでやってみたい。