※本稿は2023年11月24日に開催された「GRRMチュートリアル2023」の表面モデル作成パートの内容について、講演者自身が要点を再録したものである。
スラブモデルとは
スラブモデルは計算化学において表面系を記述する際に広く利用されるモデルである。特に表面科学や触媒反応の分野において、固体材料の表面をシミュレーションし、研究するために用いられる計算手法として用いられている。固体表面の特性はバルク材料の特性とは著しく異なることがあり、様々な化学プロセスにおいて重要な役割を果たしているため、このモデルは理論計算において非常に重要である。
スラブモデルの作成手順は以下の通り。
- 結晶構造を取得する
- 結晶構造データベースなどからcifファイルを取得する
- 格子面の切り出し
- 注目する格子面がz軸に直交するように回転操作を施す
- 結晶構造を拡大 or 削減する
- スラブモデルのxyz座標を取得する
- 結晶構造のxyz座標を取得する
- 必要に応じて構造最適化する
- 真空層を設定する
- 必要に応じて最表面を緩和する
手順2については記事「結晶構造から特定の指数面を切り出す」も併せて参照のこと。
Pt(111)面の作成
ここでは例としてPt(111)面のスラブモデルを作成する。
結晶構造を加工・調整する準備として「VESTA」のダウンロードを推奨する。VESTAは結晶構造、電子・核密度等の三次元データ、及び結晶外形の可視化プログラムである。
VESTAの利用に際しては、必ず次の論文をciteすること。
K. Momma and F. Izumi, "VESTA 3 for three-dimensional visualization of crystal, volumetric and morphology data," J. Appl. Crystallogr., 44, 1272-1276 (2011).
「ミラー指数(面)」については崎間公久氏による物理のかぎプロジェクトの記事などを参照のこと。
1. 結晶構造の取得
最も手軽なのはMaterials Projectからcifファイルを取得することである。Pt結晶のface-centered cubic (fcc)のcifファイルは以下のページから取得可能。「cif」と「cif (symmetrized)」の2種類があるが、どちらでも良い。
https://legacy.materialsproject.org/materials/mp-126/
または
https://next-gen.materialsproject.org/materials/mp-126/
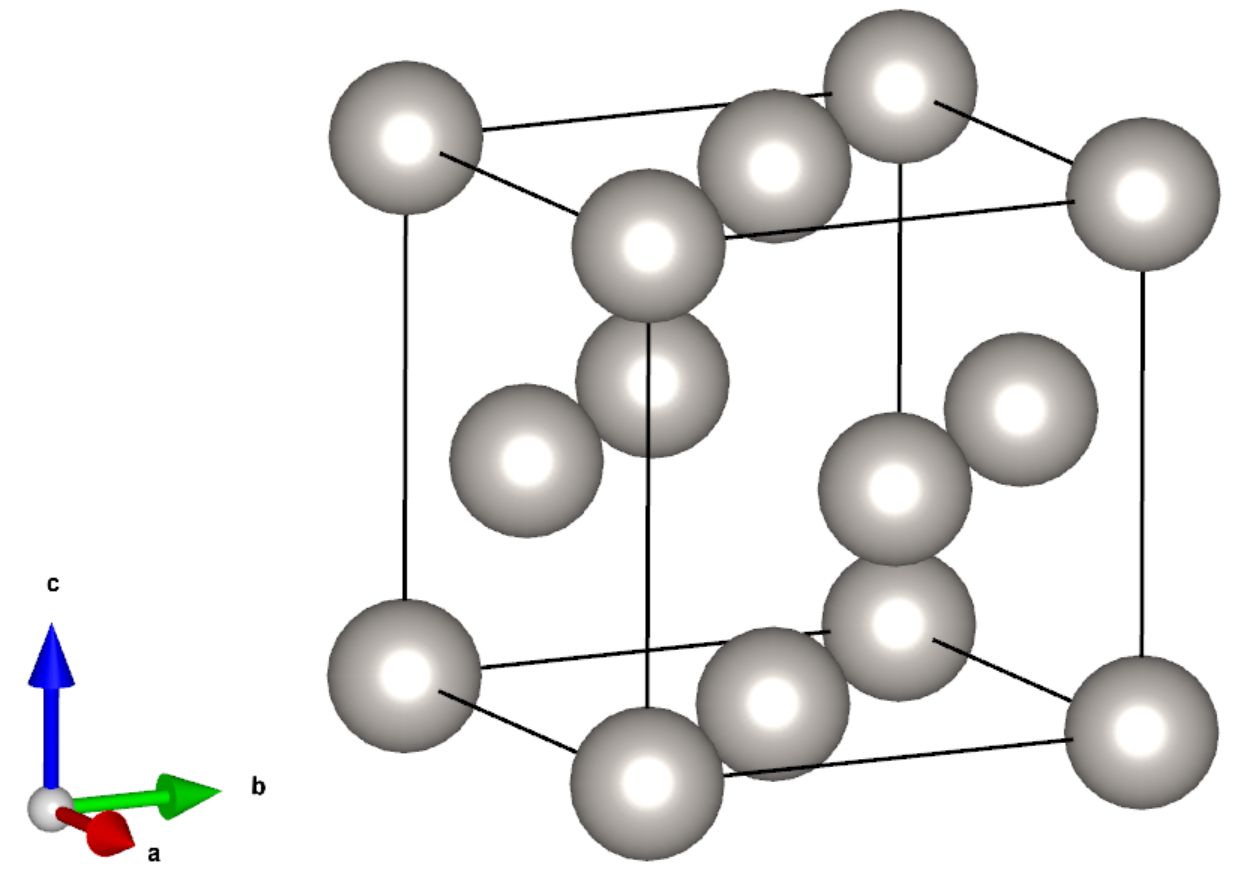
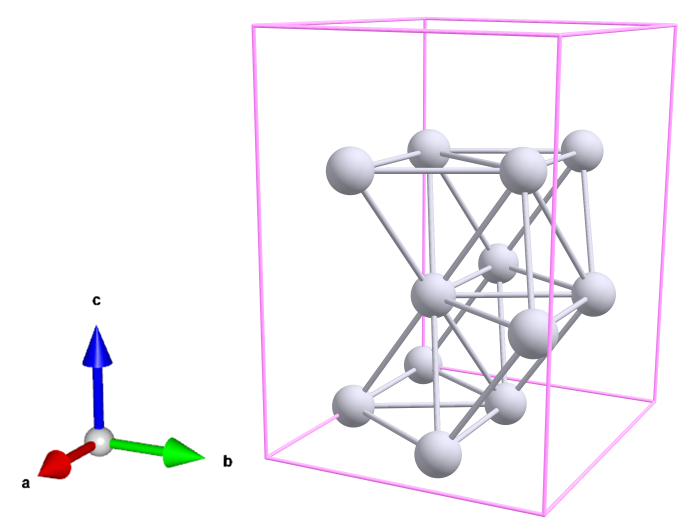
VESTAで表示すると以下の図のようになる。このab面は(001)面に相当する。
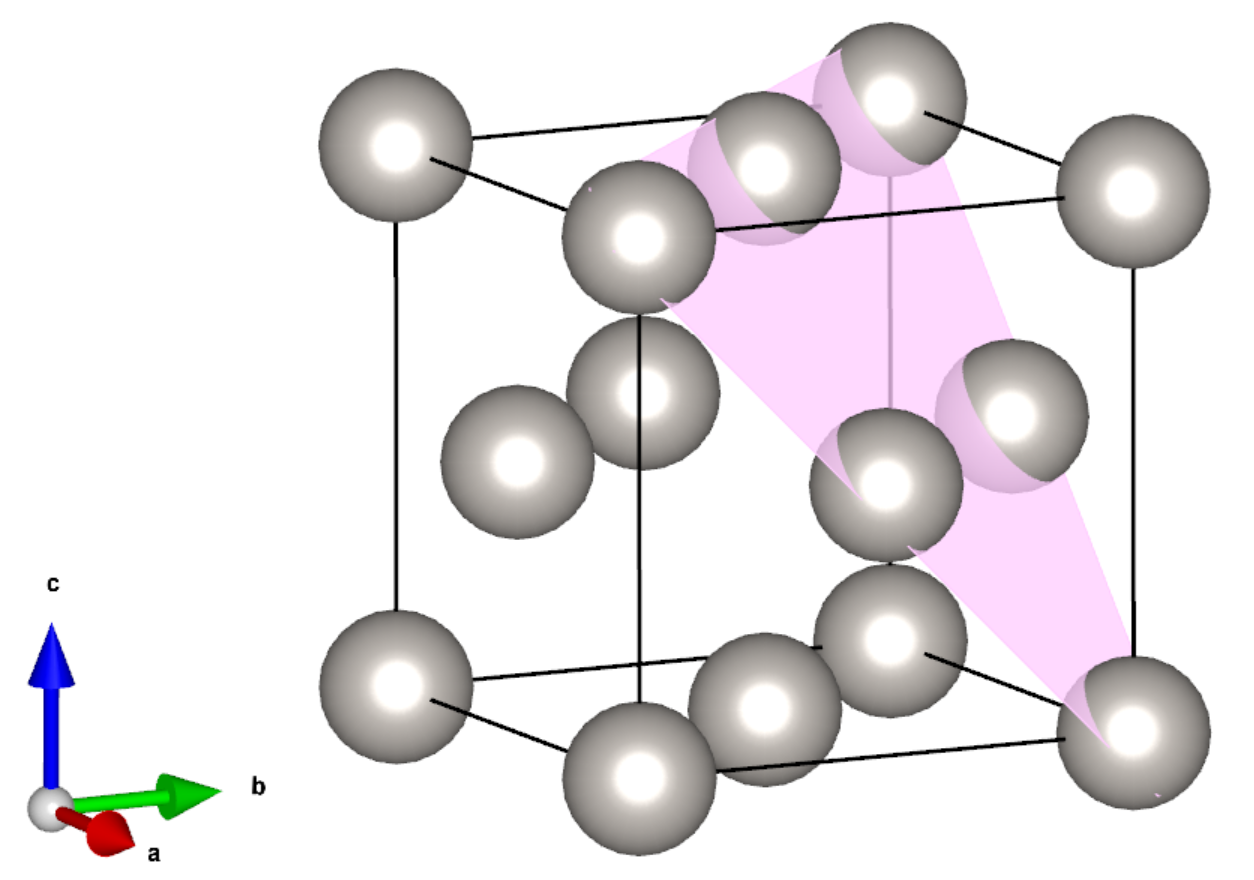
(111)面は下図の桃色の面に相当する。これがxy平面に並行になるように結晶全体に回転操作を施すのが次の手順となる。
2. 格子面の切り出し
VESTAにはセルの並進ベクトル(translation vector; TV)を再定義する機能が備わっている。これを利用してユニットセルの座標を再定義(回転操作による座標変換)する。
手順は次の通り。
- VESTAを起動して目当ての結晶のcifファイルを開く
-
次に [Edit] > [Edit Data] > [Unit Cell...] と進む
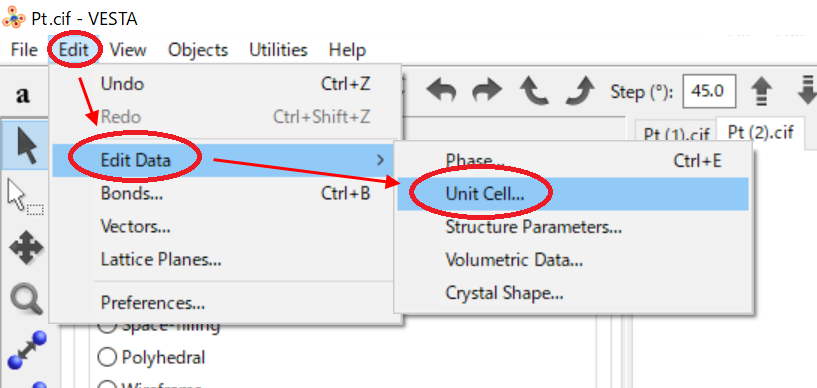
-
表示されるダイアログボックスの [Transform...] をクリック
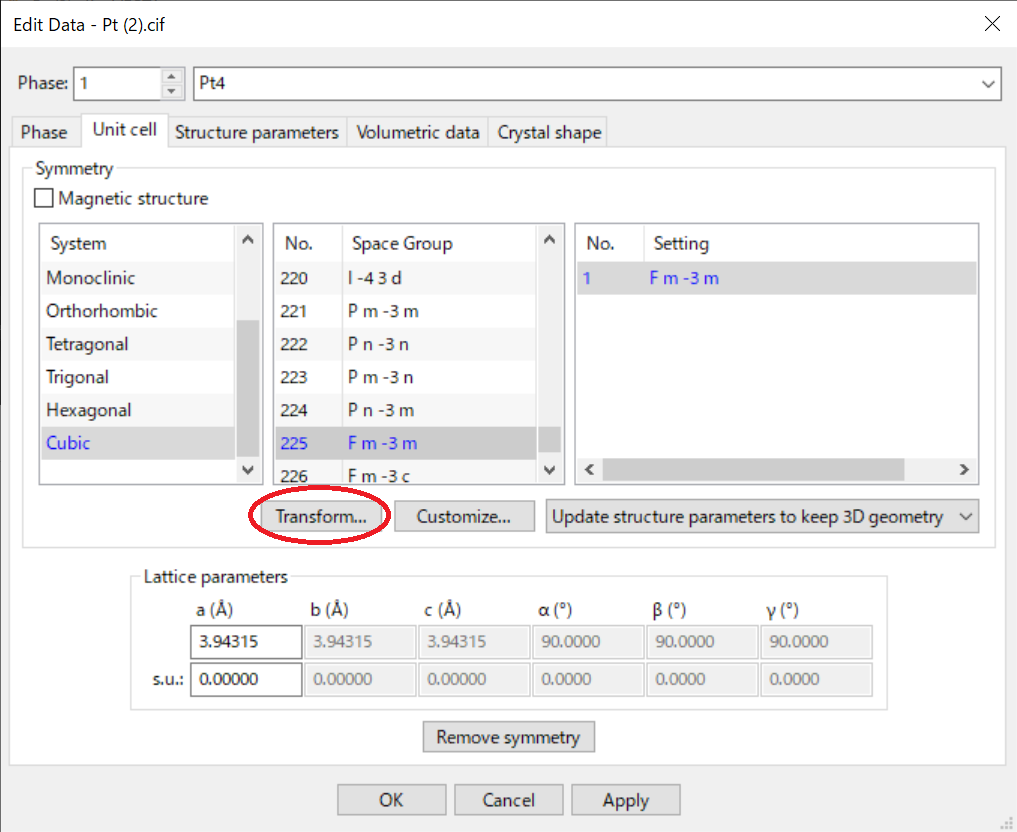
-
Rotation matrix P の成分を入力する(今回の場合は以下)
\mathbf{P}=\begin{pmatrix} 2 & 1 & 1 \\ -2 & 1 & 1 \\ 0 & -2 & 1 \end{pmatrix}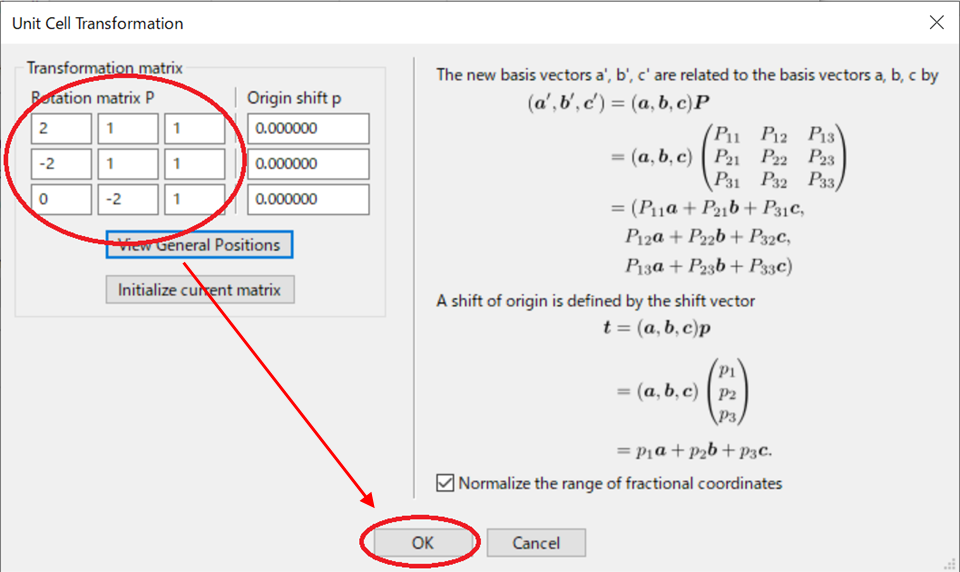
-
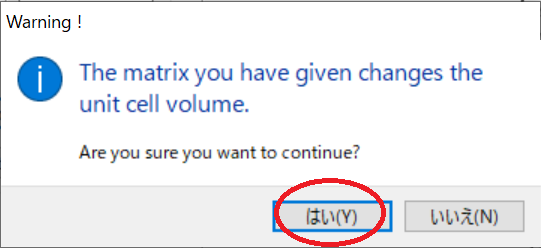
[OK]を押下すると「セルの体積が変わるが良いか?」という警告が出るので「はい(Y)」を選択
-
「Additional lattice point(s)...」のラジオボタンは「Add new equivalent positions...」を選択して[OK]を押下
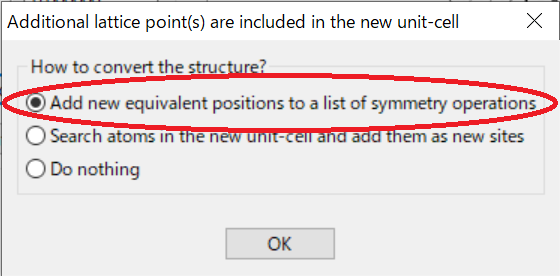
- [Apply] > [OK] の順で押下
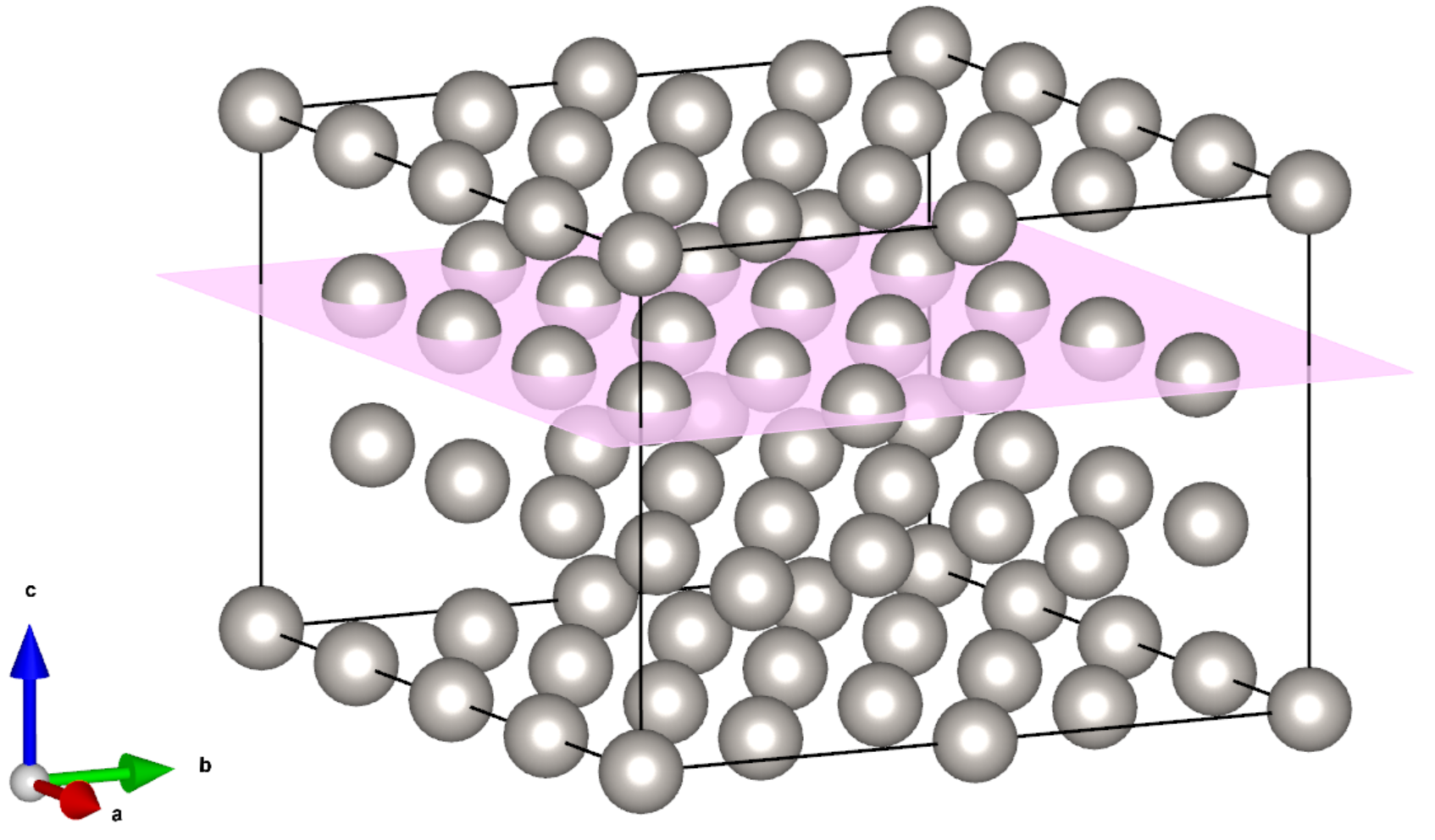
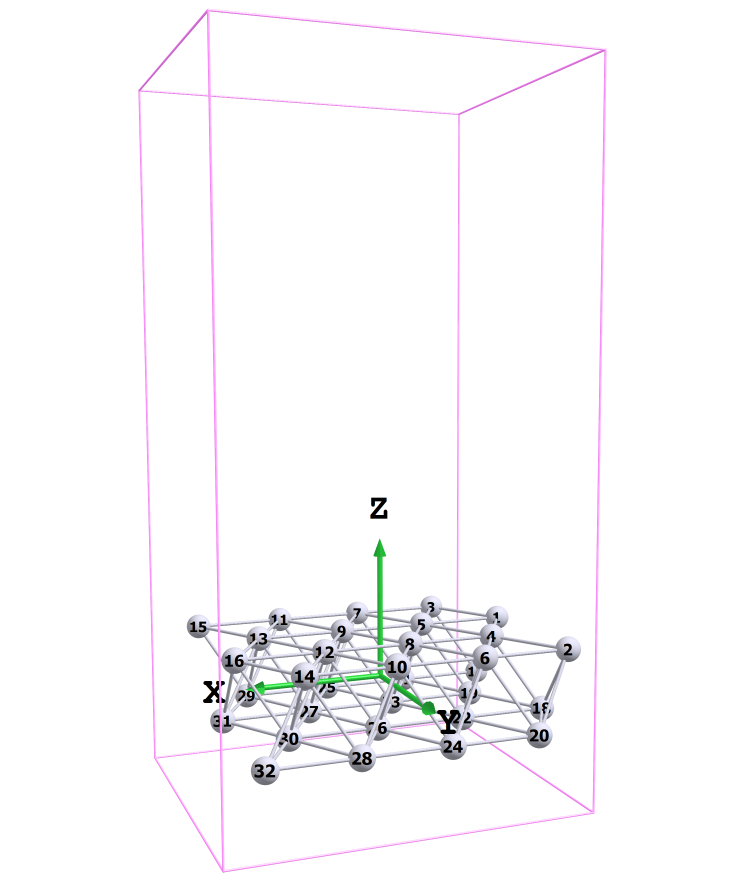
以上の手順により、下図のような新しいユニットセルが得られる。
切り出す格子面によってはユニットセル内の原子数が必ずしも保存されない。格子内の原子数が多すぎる場合は適宜手動で削除するなどする。
a,b,cの各軸とそれらの成す夾角はVESTAのOutputの欄にLattice parametersとして表示されている。
今回の場合の格子定数は次の通り。
a b c alpha beta gamma 11.15291 9.65871 6.82974 90.0000 90.0000 90.0000
3. スラブモデルのxyz座標を取得する
このようにして作成したユニットセルからスラブモデルを作成するにあたって、必要に応じて使用する計算レベルでユニットセルの最適化計算を行う。この結果をもとにスラブモデルを作成する。
GRRMプログラムを用いてセルの形状を維持したユニットセルの最適化計算を行う手順については、GRRMチュートリアルにおいて紹介しているので本稿では省略する。ここでは最適化計算用の小さいサイズのユニットセルの作成方法を述べる。
セル内の原子を削って整える方法は幾つかあるが、VESTAの原子選択モードを使ってカットしてしまうのが手っ取り早い。
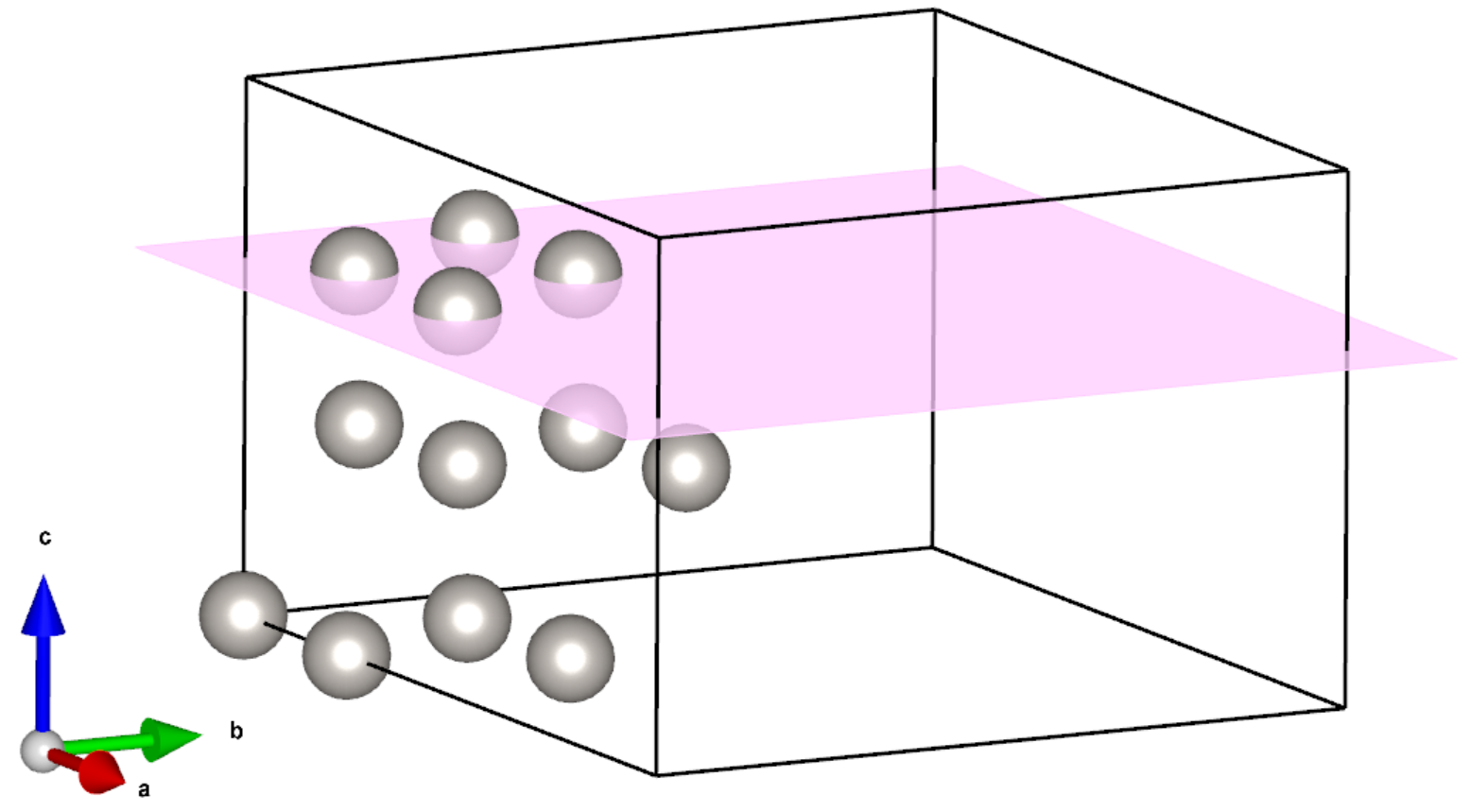
VESTAでは原点を通らない面上にも原子が描画されるので、これらをまず削除する。さらにa軸とb軸の方向について原子を半分に削減して、下図に示すPt12原子からなる構造を作る。
これをxyz形式のファイルとしてエクスポート([File] > [Export Data...])してxyz座標を取得する。取得したxyz構造をChemCraftで表示すると以下のようになる。
セルは [Tools] > [Crystallography tools] > [Cuild cells ...] でTVの情報を入力すれば描画可能。cifを読み込んだ際にもセルが表示できる。
Pt 0.000000000000 3.219569000000 4.553158000000
Pt 1.394114000000 0.804892000000 4.553158000000
Pt 2.788228000000 3.219569000000 4.553158000000
Pt 4.182342000000 0.804892000000 4.553158000000
Pt 0.000000000000 1.609784000000 2.276579000000
Pt 1.394114000000 4.024461000000 2.276579000000
Pt 2.788228000000 1.609784000000 2.276579000000
Pt 4.182342000000 4.024461000000 2.276579000000
Pt 0.000000000000 0.000000000000 0.000000000000
Pt 1.394114000000 2.414677000000 0.000000000000
Pt 2.788228000000 0.000000000000 0.000000000000
Pt 4.182342000000 2.414677000000 0.000000000000
TV 5.576455000000 0.000000000000 0.000000000000
TV 0.000000000000 4.829355000000 0.000000000000
TV 0.000000000000 0.000000000000 6.829740000000
ここで、Pt原子の座標はz座標の大きい順にソートしている。ソートにはExcelなどを利用する。
xyz座標が得られたら、中身をTVごと拡大する。ここではa軸方向に2倍、b軸方向に2倍する。反応経路探索の段階では計算コストを低減する目的で、第3層を削って2層のモデルにするとよい。
ただし、層数が多いほど吸着エネルギーの精度は向上する。
最後に15~20Å程度の真空層をz方向に確保して、下図のようなスラブモデルを得る。ここではc軸を15Åだけ伸ばして真空層を設定している。系によっては必ずしもc軸がxy平面に直行しないので、c軸に相当するTVを伸ばす際はz成分が15~20Å程度増加するように注意する。
z成分の大きい原子の順番を若くしておくとインプット作成時の苦労が減る。また、表面の原子は整列させておくのがよい。
4. 必要に応じて最表面を緩和する
酸化物表面などのように表面緩和や表面再構成が起き得る系では、必要に応じて最表面を緩和する。ただし反応経路探索のインプットにおいては必ずしも必要ではないため、ここでは省略する。
その他の系についても手順は同様である。
補足資料1:変換行列について
VESTAにおいて、変換後の新しいユニットセルは以下の式で与えられる。
{\begin{aligned}
\left(\begin{array}{c} \boldsymbol{a}^{\prime} \\ \boldsymbol{b}^{\prime} \\ \boldsymbol{c}^{\prime} \end{array}\right)
&= (\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}) \mathbf{P} \\
&= (\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c})\left(\begin{array}{lll}P_{11} & P_{12} & P_{13} \\ P_{21} & P_{22} & P_{23} \\ P_{31} & P_{32} & P_{33}\end{array}\right) \\
&= \left(\begin{array}{c} P_{11} \boldsymbol{a}+P_{21} \boldsymbol{b}+P_{31} \boldsymbol{c} \\ P_{12} \boldsymbol{a}+P_{22} \boldsymbol{b}+P_{32} \boldsymbol{c} \\ P_{13} \boldsymbol{a}+P_{23} \boldsymbol{b}+P_{33} \boldsymbol{c} \end{array}\right)
\end{aligned}
}
綺麗な(各TVの夾角が直角に近い)スラブモデルを作成するコツは次の通り。
- $\boldsymbol{c}^{\prime}$軸を注目している格子面の法線にできるだけ近付けること。
- $\boldsymbol{a}^{\prime}$軸と$\boldsymbol{b}^{\prime}$軸の夾角をできるだけ直角に近付けること。
このような条件を満たす成分の行列を入力すると上手くスラブモデルが作成できる。
1.を満たすには、一番右の列の成分$P_{13}$、$P_{23}$、$P_{33}$が格子面の法線成分になるように設定すればよい。例えば今回のPt(111)面の場合は取得したcif構造が立方体なので$(1,1,1)$にすればちょうどよい。
実際、今回用いた変換行列は
{\mathbf{P}=\begin{pmatrix} 2 & 1 & \color{red}{1} \\ -2 & 1 & \color{red}{1} \\ 0 & -2 & \color{red}{1} \end{pmatrix} }となっている。
2.を満たすには少し空間把握能力が要求される。一般にユニットセルは必ずしも直方体とは限らないので、その都度スーパーセルを作成して立体構造を眺めながら決めるのがよい。
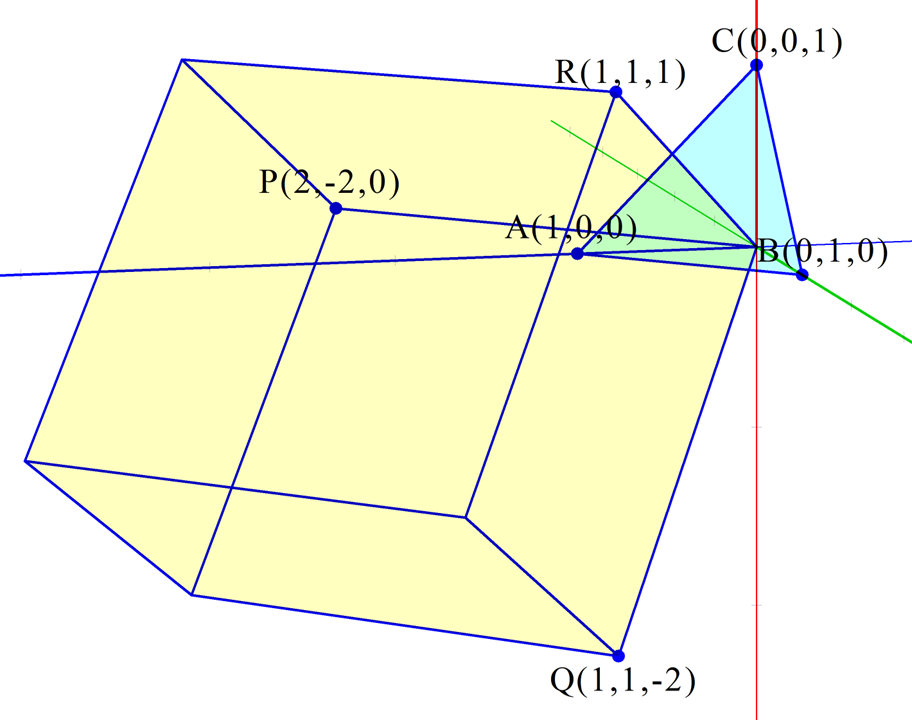
今回の場合は$(2,-2,0)$と$(1,1,-2)$のベクトルを新しい$\boldsymbol{a}^{\prime}$軸, $\boldsymbol{b}^{\prime}$軸にとっている。$\boldsymbol{a}^{\prime}$軸と$\boldsymbol{b}^{\prime}$軸を定義するベクトルの張る平面は必ず注目している格子面(今回の場合は(111)面)に平行でなければならない。また、この操作は特定のルールさえ決めれば恐らく自動化できるだろう。
参考までに、$\mathbf{P}$によって新たに作られるセルは下図のようになる。
補足資料2:各種座標
xyz coordinates for the 2-layer Pt(111) slab model (not optimized)
Pt 0.000000000000 3.219569000000 4.553158000000
Pt 0.000000000000 8.048924000000 4.553158000000
Pt 1.394114000000 0.804892000000 4.553158000000
Pt 1.394114000000 5.634247000000 4.553158000000
Pt 2.788228000000 3.219569000000 4.553158000000
Pt 2.788228000000 8.048924000000 4.553158000000
Pt 4.182342000000 0.804892000000 4.553158000000
Pt 4.182342000000 5.634247000000 4.553158000000
Pt 5.576455000000 3.219569000000 4.553158000000
Pt 5.576455000000 8.048924000000 4.553158000000
Pt 6.970569000000 0.804892000000 4.553158000000
Pt 6.970569000000 5.634247000000 4.553158000000
Pt 8.364683000000 3.219569000000 4.553158000000
Pt 8.364683000000 8.048924000000 4.553158000000
Pt 9.758797000000 0.804892000000 4.553158000000
Pt 9.758797000000 5.634247000000 4.553158000000
Pt 0.000000000000 1.609784000000 2.276579000000
Pt 0.000000000000 6.439139000000 2.276579000000
Pt 1.394114000000 4.024461000000 2.276579000000
Pt 1.394114000000 8.853816000000 2.276579000000
Pt 2.788228000000 1.609784000000 2.276579000000
Pt 2.788228000000 6.439139000000 2.276579000000
Pt 4.182342000000 4.024461000000 2.276579000000
Pt 4.182342000000 8.853816000000 2.276579000000
Pt 5.576455000000 1.609784000000 2.276579000000
Pt 5.576455000000 6.439139000000 2.276579000000
Pt 6.970569000000 4.024461000000 2.276579000000
Pt 6.970569000000 8.853816000000 2.276579000000
Pt 8.364683000000 1.609784000000 2.276579000000
Pt 8.364683000000 6.439139000000 2.276579000000
Pt 9.758797000000 4.024461000000 2.276579000000
Pt 9.758797000000 8.853816000000 2.276579000000
TV 11.152910000000 0.000000000000 0.000000000000
TV 0.000000000000 9.658710000000 0.000000000000
TV 0.000000000000 0.000000000000 21.829740000000
xyz coordinates for the optimized unit cells
Pt -0.046019344478 3.246150408237 4.603325535366
Pt 1.378874466057 0.778328229405 4.603133001891
Pt 2.803535649485 3.246203222511 4.603291606219
Pt 4.228441228515 0.778348039592 4.603197847389
Pt -0.046022421522 1.600966562853 2.276545323484
Pt 1.378808140908 4.068640812784 2.276521560607
Pt 2.803536593815 1.600941249568 2.276605713874
Pt 4.228369187709 4.068770628458 2.276539113016
Pt -0.046041686355 -0.044282934734 -0.050024833423
Pt 1.378807518954 2.423453760747 -0.050107134640
Pt 2.803445855284 -0.044275001037 -0.050035153616
Pt 4.228316811628 2.423521021613 -0.050044580177
TV 5.699119888090 -0.000000000000 0.000000000000
TV 0.000000000000 4.935585981983 0.000000000000
TV -0.000000000000 0.000000000000 6.979973310010
ENERGY = -334.904841336624
Pt -0.052627998133 3.237005492441 4.613534016269
Pt 1.376547305680 0.787592163078 4.613430939256
Pt 2.805653281108 3.236993848048 4.613466960513
Pt 4.234880337379 0.787520417831 4.613431766320
Pt -0.052460156221 1.604143725424 2.276496989656
Pt 1.376652044881 4.053123896714 2.276641270948
Pt 2.805851210794 1.604042484125 2.276502461513
Pt 4.234933348795 4.053136786694 2.276595177103
Pt -0.052507728002 -0.028728183600 -0.060302555819
Pt 1.376605455528 2.420360465223 -0.060234804622
Pt 2.805691617208 -0.028748092539 -0.060350031175
Pt 4.234833280984 2.420322996559 -0.060264189961
TV 5.716541980275 -0.000000000000 -0.000000000000
TV -0.000000000000 4.898545141936 0.000000000000
TV -0.000000000000 0.000000000000 7.010637970666
ENERGY = -334.905100676933
TV-Shape=FixとTV-Angle=Fixの計算結果の差は 0.68 kJ/mol で、ほぼ誤差の範囲と言える。
xyz coordinates for the 3-layer Pt(111) slab model
Pt -0.046019344000 3.246150408000 4.603325535000
Pt -0.046019344000 8.181736390000 4.603325535000
Pt 5.653100544000 3.246150408000 4.603325535000
Pt 5.653100544000 8.181736390000 4.603325535000
Pt 2.803535649000 3.246203223000 4.603291606000
Pt 2.803535649000 8.181789204000 4.603291606000
Pt 8.502655538000 3.246203223000 4.603291606000
Pt 8.502655538000 8.181789204000 4.603291606000
Pt 4.228441229000 0.778348040000 4.603197847000
Pt 4.228441229000 5.713934022000 4.603197847000
Pt 9.927561117000 0.778348040000 4.603197847000
Pt 9.927561117000 5.713934022000 4.603197847000
Pt 1.378874466000 0.778328229000 4.603133002000
Pt 1.378874466000 5.713914211000 4.603133002000
Pt 7.077994354000 0.778328229000 4.603133002000
Pt 7.077994354000 5.713914211000 4.603133002000
Pt 2.803536594000 1.600941250000 2.276605714000
Pt 2.803536594000 6.536527232000 2.276605714000
Pt 8.502656482000 1.600941250000 2.276605714000
Pt 8.502656482000 6.536527232000 2.276605714000
Pt -0.046022422000 1.600966563000 2.276545323000
Pt -0.046022422000 6.536552545000 2.276545323000
Pt 5.653097467000 1.600966563000 2.276545323000
Pt 5.653097467000 6.536552545000 2.276545323000
Pt 4.228369188000 4.068770628000 2.276539113000
Pt 4.228369188000 9.004356610000 2.276539113000
Pt 9.927489076000 4.068770628000 2.276539113000
Pt 9.927489076000 9.004356610000 2.276539113000
Pt 1.378808141000 4.068640813000 2.276521561000
Pt 1.378808141000 9.004226795000 2.276521561000
Pt 7.077928029000 4.068640813000 2.276521561000
Pt 7.077928029000 9.004226795000 2.276521561000
Pt -0.046041686000 -0.044282935000 -0.050024833000
Pt -0.046041686000 4.891303047000 -0.050024833000
Pt 5.653078202000 -0.044282935000 -0.050024833000
Pt 5.653078202000 4.891303047000 -0.050024833000
Pt 2.803445855000 -0.044275001000 -0.050035154000
Pt 2.803445855000 4.891310981000 -0.050035154000
Pt 8.502565743000 -0.044275001000 -0.050035154000
Pt 8.502565743000 4.891310981000 -0.050035154000
Pt 4.228316812000 2.423521022000 -0.050044580000
Pt 4.228316812000 7.359107004000 -0.050044580000
Pt 9.927436700000 2.423521022000 -0.050044580000
Pt 9.927436700000 7.359107004000 -0.050044580000
Pt 1.378807519000 2.423453761000 -0.050107135000
Pt 1.378807519000 7.359039743000 -0.050107135000
Pt 7.077927407000 2.423453761000 -0.050107135000
Pt 7.077927407000 7.359039743000 -0.050107135000
TV 11.398239776180 0.000000000000 0.000000000000
TV 0.000000000000 9.871171963966 0.000000000000
TV 0.000000000000 0.000000000000 21.979973310010
Pt -0.052627998000 3.237005492000 4.613534016000
Pt -0.052627998000 8.135550634000 4.613534016000
Pt 5.663913982000 3.237005492000 4.613534016000
Pt 5.663913982000 8.135550634000 4.613534016000
Pt 2.805653281000 3.236993848000 4.613466961000
Pt 2.805653281000 8.135538990000 4.613466961000
Pt 8.522195261000 3.236993848000 4.613466961000
Pt 8.522195261000 8.135538990000 4.613466961000
Pt 4.234880337000 0.787520418000 4.613431766000
Pt 4.234880337000 5.686065560000 4.613431766000
Pt 9.951422318000 0.787520418000 4.613431766000
Pt 9.951422318000 5.686065560000 4.613431766000
Pt 1.376547306000 0.787592163000 4.613430939000
Pt 1.376547306000 5.686137305000 4.613430939000
Pt 7.093089286000 0.787592163000 4.613430939000
Pt 7.093089286000 5.686137305000 4.613430939000
Pt 1.376652045000 4.053123897000 2.276641271000
Pt 1.376652045000 8.951669039000 2.276641271000
Pt 7.093194025000 4.053123897000 2.276641271000
Pt 7.093194025000 8.951669039000 2.276641271000
Pt 4.234933349000 4.053136787000 2.276595177000
Pt 4.234933349000 8.951681929000 2.276595177000
Pt 9.951475329000 4.053136787000 2.276595177000
Pt 9.951475329000 8.951681929000 2.276595177000
Pt 2.805851211000 1.604042484000 2.276502462000
Pt 2.805851211000 6.502587626000 2.276502462000
Pt 8.522393191000 1.604042484000 2.276502462000
Pt 8.522393191000 6.502587626000 2.276502462000
Pt -0.052460156000 1.604143725000 2.276496990000
Pt -0.052460156000 6.502688867000 2.276496990000
Pt 5.664081824000 1.604143725000 2.276496990000
Pt 5.664081824000 6.502688867000 2.276496990000
Pt 1.376605456000 2.420360465000 -0.060234805000
Pt 1.376605456000 7.318905607000 -0.060234805000
Pt 7.093147436000 2.420360465000 -0.060234805000
Pt 7.093147436000 7.318905607000 -0.060234805000
Pt 4.234833281000 2.420322997000 -0.060264190000
Pt 4.234833281000 7.318868138000 -0.060264190000
Pt 9.951375261000 2.420322997000 -0.060264190000
Pt 9.951375261000 7.318868138000 -0.060264190000
Pt -0.052507728000 -0.028728184000 -0.060302556000
Pt -0.052507728000 4.869816958000 -0.060302556000
Pt 5.664034252000 -0.028728184000 -0.060302556000
Pt 5.664034252000 4.869816958000 -0.060302556000
Pt 2.805691617000 -0.028748093000 -0.060350031000
Pt 2.805691617000 4.869797049000 -0.060350031000
Pt 8.522233597000 -0.028748093000 -0.060350031000
Pt 8.522233597000 4.869797049000 -0.060350031000
TV 11.433083960550 0.000000000000 0.000000000000
TV 0.000000000000 9.797090283872 0.000000000000
TV 0.000000000000 0.000000000000 22.010637970666