【はじめに】
本稿は計算化学に関する内容で、VESTAプログラムを利用し、結晶構造(この場合、特にcif形式のファイル)から特定の指数の面を切り出してスラブモデルを作成する手順の例を示すものです。細かい用語の解説は特にしていません。
(111)面を切り出す
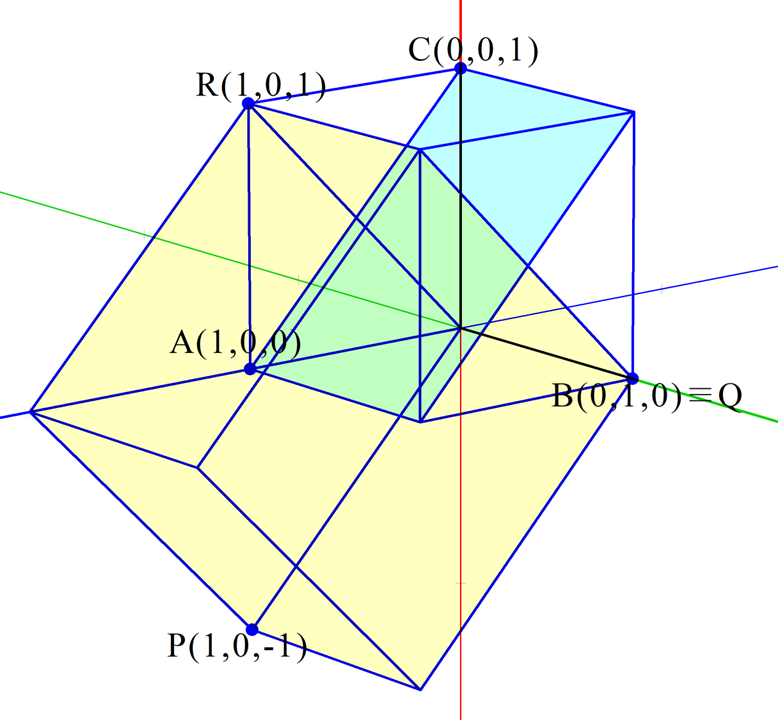
例えば「立方体の」ユニットセルをもつ結晶の$(111)$面は下図のようになっています。ここでは各頂点が$xyz$座標系において$\mathrm{A}(1,0,0)$、$\mathrm{B}(0,1,0)$、$\mathrm{C}(0,0,1)$と定義されているものとします。

スラブモデルを作るにはこれに平行な面を面の一つにもつ直方体(より一般には平行六面体)を作成する必要があります。
そのような直方体のうち、3辺が直角に交わるものには例えば下図のようなものがあります。

つまり、新しい座標軸を図中の$\overrightarrow{\mathrm{OP}}$、$\overrightarrow{\mathrm{OQ}}$、$\overrightarrow{\mathrm{OR}}$の向きに取り直すことで、$(111)$面(に平行な面)を$XY$平面とする新たな$XYZ$座標系を定義することができます。
このような座標変換を行うには、「VESTA」のユニットセル変換機能を利用するのが手っ取り早いです。手順は次の通りです。
- VESTAを起動して目当ての結晶のcifファイルを開く。
- 次に [Edit] > [Edit Data] > [Unit Cell...] と進む。
- 表示されるダイアログボックスの [Transform...] をクリック。
- Rotation matrix P の成分を入力する。今回の場合は以下。
\mathbf{P}=\begin{pmatrix}
2 & 1 & 1 \\
-2 & 1 & 1 \\
0 & -2 & 1
\end{pmatrix}
- [OK]を押下すると「セルの体積が変わるが良いか?」という警告が出るので「はい(Y)」を選択。
- 「Additional lattice point(s)...」のラジオボタンは「Add new equivalent positions...」を選択して[OK]を押下。
- [Apply] > [OK] の順で押下。
以上の手順により$(111)$面を$XY$平面とする$XYZ$座標系に変換された結晶構造が得られます。
例えばPd結晶の場合、ユニットセルは次のようになっています。
これに対し上記の変換を施すと、次のようになります。
あとは適当に$(111)$方向(図中c軸の方向)に15~20Å程度の真空層を確保してやれば$(111)$面のスラブモデルの完成です。表面積が大きすぎる場合は、変換行列$\mathbf{P}$を上手く調節するか、変換後の結晶のサイズを削減してください。単位格子が立方体でない場合、上記の変換行列では$XYZ$座標系の3軸が直交しません。そのままでもスラブモデルを作成することはできますが、色々な電子状態計算の都合上、できるだけ3軸の夾角が直角に近付くような軸の取り方を目指しましょう。
(101)面を切り出す
切り出す手順は二元系でも変わりません。ここではCuO結晶の$(101)$面を切り出してみます。

CuO結晶の最安定相は単斜晶系のテノライトです。
最も単純な変換は下図のようなセルの取り方になります。
このときの変換行列$\mathbf{P}$は
\mathbf{P}=\begin{pmatrix}
1 & 0 & 1 \\
0 & 1 & 0 \\
-1 & 0 & 1
\end{pmatrix}
となりますが、このままだと$Y$方向の辺が短くなってしまうので、新しい$b$軸方向を2倍した$\mathbf{P}^{\prime}$を用いることにします。
\mathbf{P}^{\prime}=\begin{pmatrix}
1 & 0 & 1 \\
0 & \color{red}{2} & 0 \\
-1 & 0 & 1
\end{pmatrix}
これを用いると以下のように丁度良いサイズの結晶格子が得られます。このセルの$ab$平面は正しく$(101)$面に相当しています。

六方晶系の面を切り出す
ZnO結晶は「ウルツ鉱型結晶構造」の名前の由来であるZnS結晶の類縁体で、下図のような六方晶系(Hexagonal crystal family)の結晶構造をとります。

(画像の出典)B. Meyer, D. Marx, “Density-functional study of the structure and stability of ZnO surfaces,” Phys. Rev. B 2003, 67, 035403.
六方晶系の面指数は下図のように $\vec{a_1}$、$\vec{a_2}$、$\vec{a_3}$、$\vec{c_{}}$ の4つのベクトルによって定義されます。面指数の名付けは $(a_1 a_2 a_3 c)$ のようになります。例えば図中Aの面は$(11\bar{2}0)$面、Bの面は$(1\bar{1}00)$面、Cの面は$(0001)$面と表されます。

(画像の出典)Aki Takigawa, S. Tachibana, H. Nagahara, K. Ozawa, “EVAPORATION AND CONDENSATION KINETICS OF CORUNDUM: THE ORIGIN OF THE 13 μm FEATURE OF OXYGEN-RICH AGB STARS,” ApJS 2015, 218, 2.
六方晶の単位格子は基本的に、六角柱から $\vec{a_1}$、$\vec{a_2}$、$\vec{c_{}}$ を辺とする四角柱を切り出した構造で与えられます。ZnOの場合、単位格子をVESTAで表示すると次のようになります。図中$b$軸が上図の$a_2$軸に相当しています。

ここで、ZnO$(10\bar{1}0)$面を切り出してみます。$(10\bar{1}0)$面は下図に示す面であり既に単位格子の面の一つとして露出しているので、並進ベクトル(TV)を新しく取り直すだけでOKです。

これをスラブモデルにする変換行列$\mathbf{P}$は、例えば
\mathbf{P}=\begin{pmatrix}
0 & 0 & 2 \\
2 & 0 & 1 \\
0 & 1 & 0
\end{pmatrix}
となります。これを施してやると下図のように$ab$平面が$(10\bar{1}0)$面に平行な直方体のセルが得られます。この$c$軸方向は$(10\bar{1}0)$方向に相当するので、この軸方向に真空層を確保すれば$(10\bar{1}0)$面のスラブモデルになります。

因みに、ZnO結晶のような3回対称性をもつ六方晶では、$(1\bar{1}00)$、$(10\bar{1}0)$、$(100\bar{1})$およびその面対称なファセットはすべて同一の面を指しています。文献によって表記が異なることがあるので要注意。
変換行列の数学について
最後に、変換行列の仕組みについて触れておきます。
オリジナルの並進ベクトル(TV)である$(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c})$に対して、変換行列$\mathbf{P}$は以下のように作用しています(VESTAが表示するダイアログボックスにも全く同じ記載があります)。
\begin{aligned}
\left(\begin{array}{c} \boldsymbol{a}^{\prime} \\ \boldsymbol{b}^{\prime} \\ \boldsymbol{c}^{\prime} \end{array}\right)
&= (\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}) \mathbf{P} \\
&= (\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c})\left(\begin{array}{lll}P_{11} & P_{12} & P_{13} \\ P_{21} & P_{22} & P_{23} \\ P_{31} & P_{32} & P_{33}\end{array}\right) \\
&= \left(\begin{array}{c} P_{11} \boldsymbol{a}+P_{21} \boldsymbol{b}+P_{31} \boldsymbol{c} \\ P_{12} \boldsymbol{a}+P_{22} \boldsymbol{b}+P_{32} \boldsymbol{c} \\ P_{13} \boldsymbol{a}+P_{23} \boldsymbol{b}+P_{33} \boldsymbol{c} \end{array}\right)
\end{aligned}
ここで行列$\mathbf{P}$の成分$P_{ij}$は実数(スカラー量)です。この座標変換を用いて、ユニットセルおよびその内部の原子の座標を丸ごと新たな座標系に変換することができます。
ここまでの説明に登場してきた変換行列の成分は、既存のTV$(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c})$から新規座標系の新しいTV$(\boldsymbol{a}^{\prime}, \boldsymbol{b}^{\prime}, \boldsymbol{c}^{\prime})$をどのように表現するかを決めてから逆算して求めています。$(\boldsymbol{a}^{\prime}, \boldsymbol{b}^{\prime}, \boldsymbol{c}^{\prime})$は一意には決まりませんが、$(\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c})$の線形結合で必ず表現できるので、変換行列$\mathbf{P}$は任意に与えることができます。
文章で説明すると大仰な印象になってしまいますが、視覚的に捉えれば難しいことは言っていません。なお、$\boldsymbol{a}$、$\boldsymbol{b}$、$\boldsymbol{c}$ および $\boldsymbol{a}^{\prime}$、$\boldsymbol{b}^{\prime}$、$\boldsymbol{c}^{\prime}$ はいずれも空間ベクトルであることに注意。
以上の手順により、自由自在にユニットセルのあらゆる面を切り出すことができます。空間ベクトルの認識能力がある程度要求されますが、ミラー指数はほとんどの場合で単純な整数となるので慣れれば難しくありません。

