はじめに
Pythonを使って構造方程式モデリング(Structural Equation Modeling, SEM)を実行する必要がありました。
しかし、参考となる日本語記事が皆無に近かったため、自分でまとめ記事を書くことにしました。
構造方程式モデリングとは
- 構造方程式モデリングとは、共分散構造分析とも呼ばれます。
- SEM(えす・いー・えむ)と呼んだり、SEM(せむ)と呼ぶひとがいます。
構造方程式モデリングの歴史
- 1960年代から1970年代にかけて、コンピュータに実装するカタチで生まれたと言われています
アルゴリズムの種類
- 連立方程式回帰法
- 反復最尤アルゴリズム
- 反復正準相適合アルゴリズム
など、色々なアルゴリズムがあります。ここを深堀り始めると、もう戻ってこれなさそうです。
ですから、今回は割愛します。
構造方程式モデリングの魅力
- 個人的には、因子モデルと回帰モデルを同時に実行できることが最大の魅力だと思います。
- また、「まず、こういうモデルであろう」と仮説モデルを立て、そのままモデルをプログラムにして実行できます。
- つまり、頭で考えたことをすぐにカタチにできる柔軟性の高い分析手法ということです。
- なので、議論を最小にして、繰り返し繰り返しSEMをおこない、モデルを洗練させていくことができます。
観測変数と潜在変数
構造方程式モデリングを実行するためには、観測変数と潜在変数という考え方を知っておく必要があります。
観測変数
- その名の通り、**「観測できる変数」**です。
- 具体的に言えば、大学での研究や実験、ビジネスで実際に収集できるデータのことを指します。
- 構造方程式モデリングの教科書によく出てくる事例は「文系学力」と「国語、数学…」などの科目です。
- 観測変数は、得点として観測できる「国語」や「数学」にあたります。
潜在変数
- 観測できる変数の背後に隠れている変数です。
- これを因子モデルでは、**因子(あるいは共通因子)**と呼びます。
- マッチングアプリでは、「年収」「職業」「住まい」「趣味」などのデータを収集(≒観測)できますが、その背後にある「モテるかどうか(モテ度)」は観測できません。
- おそらく多くの人々が、なんとなく**「モテるヒト(モテ度が高い人物)」がいることを認識しています。モテ度という指標がマッチングというモデルに組み込まれていると知っています。しかし、データとしては取得することがむずかしい。**こういう変数を潜在変数といいます。
実務への応用
- そういうわけで、社会学・心理学などの簡単にデータとして取得できない変数(潜在変数)が必要な学術分野で活用されています。
- 実際のところ、ビジネスでもデータとして取得できないモノゴトが多いので、顧客理解やビジネス構造理解に応用できます。
パス図
観測変数と潜在変数の違いがわかってきたら、パス図も理解する必要があります。
なぜならば、このパス図がいわゆる仮説モデル(たぶん、これとあれが関係していると思うんだよなぁー的な)の設計図になるからです。
パス図の書き方
- 観測変数は四角形
- 潜在変数は円・楕円形
- 因果関係は単方向矢印(実践・直線が多い)
- 共分散(相関関係)は双方向矢印(点線・曲線が多い)
まずは、変数を書いていきます。取得できるデータから図示していくと思うので、観測変数から書いていきます。
それらの観測変数がどんな見えない変数から導き出されているのかを考えます。
そして、導き出した変数に対して単方向の矢印を書きます。
上記のパス図では、y1, y2, y3, y4は背後にあるdem60から導き出された観測変数であると考えているため、潜在変数から観測変数に対して矢印が伸びています。また、図が複雑になるため、現時点では、共分散の矢印をプロットしていません。
なぜ、semopyなのか?
ここまでの基礎知識があれば、だれもが構造方程式モデリングを遊べるでしょう。
実際に、semopyで遊んでみるまえに、そもそもなぜ今のタイミングでPythonでSEMなのでしょうか?
- 機械学習モデルのライブラリが豊富なPythonは、SEMを実行できないという弱みがありました。
- 統計数理モデルのライブラリは統計解析のプログラミング言語として強いRなどがあります。
- ですから、RやSPSSなどを使ってSEMを実行し、どうしてもPythonでやりたい場合は、フルスクラッチで書くかPypeRを使って力技でPythonとつなげる方法が主流でした。
- しかし、semopyがバージョン2.0となって実用性が高まりました。
- これから、本ライブラリの利用者が増えていくと、使えるメソッドも増えていくと思います
そこで、semopyを使ってPython1本で構造方程式モデリングを実行してみます
semopyを使って構造方程式モデリングを実行する
本当はオリジナルのデータセットを用意して遊んでみたいのですが、時間がないので、semopy: Structural Equation Modeling in Python のサンプルを使って、手順をまとめます。
0. ライブラリのインストール
pipコマンドによるインストール
pip install semopy
gitコマンドによるインストール
git clone https://gitlab.com/georgy.m/semopy
1. semopyをインポートする
-
as semと略称設定する場合は、semopyと書いてある部分はsemと書き換えてください
# semopyをインポートする
import semopy as sem
# 仮説モデルをインスタンス化するModelもインポートする
from semopy import Model
-
from semopy import Modelを実行しなくても、正しく実行できました
2. データセットを用意する
今回はサンプルのデータセットを利用するので、下記のコードでサンプルデータを取得します。
# semopyライブラリからサンプルデータをインポートする
from semopy.examples import political_democracy
# サンプルデータ取得し、dataに代入する
data = political_democracy.get_data()
data
- このような結果が表示されればOKです。
データ型変換
- semopyは、データ型がfloat64でなければ正しく実行できません
- データ型が違う場合は、型変換を行ったほうが良いでしょう
- サンプルデータは型変換の必要がないので、そのまま進めます
# データ型の確認
data.dtypes
# 実行結果
y1 float64
y2 float64
y3 float64
y4 float64
y5 float64
y6 float64
y7 float64
y8 float64
x1 float64
x2 float64
x3 float64
dtype: object
3. モデルを設定する
仮説モデルの設定内容を確認する
- サンプルデータでは、すでに仮説モデルを記述されています
-
get_mode()で仮説モデルの設定内容を取得します - 変数descに代入し、
print()してみましょう
desc = political_democracy.get_model()
print(desc)
# 実行結果
# measurement model
ind60 =~ x1 + x2 + x3
dem60 =~ y1 + y2 + y3 + y4
dem65 =~ y5 + y6 + y7 + y8
# regressions
dem60 ~ ind60
dem65 ~ ind60 + dem60
# residual correlations
y1 ~~ y5
y2 ~~ y4 + y6
y3 ~~ y7
y4 ~~ y8
y6 ~~ y8
- これらはすべてstr型(文字列)で記述します
- Rでの記述方法とほとんど一緒です(回帰モデルの
~の数が違ったりするので、すこし修正が必要です)
仮説モデルを設定する
# 仮説モデルを、変数descに代入する
desc = '''
# measurement model
ind60 =~ x1 + x2 + x3
dem60 =~ y1 + y2 + y3 + y4
dem65 =~ y5 + y6 + y7 + y8
# regressions
dem60 ~ ind60
dem65 ~ ind60 + dem60
# residual correlations
y1 ~~ y5
y2 ~~ y4 + y6
y3 ~~ y7
y4 ~~ y8
y6 ~~ y8
'''
- str型で記述するということは、変数に代入するときに
'''で囲めばいいというシンプルなお話です
記述方法
- 記述方法を学ぶにあたって、データセットを深く理解する必要があります。
- political_democracyとは、PoliticalDemocracy: Industrialization And Political Democracy Dataset in lavaan: Latent Variable Analysisこれを指すようです
使用するデータセットの概要
| 物理名 | 論理名|日本語訳 | 型 | 欠損数 |
|---|---|---|---|
| y1 | 1960年の報道の自由に関する専門家による評価 | float64 | 0 |
| y2 | 1960年の政治的反対の自由 | float64 | 0 |
| y3 | 1960年の選挙の公平性 | float64 | 0 |
| y4 | 1960年に選出された立法府の有効性 | float64 | 0 |
| y5 | 1965年の報道の自由に関する専門家による評価 | float64 | 0 |
| y6 | 1965年の政治的反対の自由 | float64 | 0 |
| y7 | 1965年の選挙の公平性 | float64 | 0 |
| y8 | 1965年に選出された立法府の有効性 | float64 | 0 |
| x1 | 1960年の一人当たりの国民総生産(GNP) | float64 | 0 |
| x2 | 1960年の一人当たりの無生物のエネルギー消費量 | float64 | 0 |
| x3 | 1960年の産業における労働力の割合 | float64 | 0 |
構造方程式|潜在変数 =~ 観測変数
- 1960年の産業(Industry1960, ind60)という潜在変数は、GNPとエネルギー消費量と労働力の割合という観測変数を導いている
- 1960年の民主主義(Democracy1960, demo60)という潜在変数は、専門家による報道の評価、政治に反対できる自由度、選挙の公平性、政府の有効性という観測変数を導いている
- 1966年の民主主義(Democracy1965, demo65)という潜在変数は、専門家による報道の評価、政治に反対できる自由度、選挙の公平性、政府の有効性という観測変数を導いている
# measurement model
ind60 =~ x1 + x2 + x3
dem60 =~ y1 + y2 + y3 + y4
dem65 =~ y5 + y6 + y7 + y8
測定方程式|変数(結果) ~ 変数(説明)
- 1960年の産業(Industry1960, ind60)と1960年の民主主義(Democracy1960, demo60)は、同じ時期だから因果関係はあるだろう
- 1965年の民主主義(Democracy1965, demo65)は、1960年の産業(Industry1960, ind60)と1960年の民主主義(Democracy1960, demo60)という過去のデータで説明できるだろう
# regressions
dem60 ~ ind60
dem65 ~ ind60 + dem60
残差相関|変数 ~~ 変数
- 1960年の報道の自由(y1)は1965年の報道の自由(y5)と相関があるだろう
- 1960年の政治に反対できる自由度(y2)は同じ時期の選挙の公平性(y4)と1965年の政治に反対できる自由度(y6)で説明できるだろう
などなど…
# residual correlations
y1 ~~ y5
y2 ~~ y4 + y6
y3 ~~ y7
y4 ~~ y8
y6 ~~ y8
そんなわけで、仮説モデルを作りました。
4. 学習を実行する
semopyは下記の通り、いろいろなモジュールを持っています
from see import see
see(semopy)
# 実行結果
ismodule help() .Model()
.ModelEffects() .ModelMeans() .calc_stats()
.constraints .create_regularization() .efa
.estimate_means() .examples .gather_statistics()
.inspector .means .model .model_base
.model_effects .model_means .multigroup .name
.optimizer .parser .plot .polycorr
.regularization .semplot() .solver
.startingvalues .stats .utils
ですが、SEMを実行するだけなら、機械学習モデルを構築する手順とほぼ同様のプロセスなので、簡単です。
model()|使用するモデルを用意
-
Model()に仮説モデル(今回の場合はdesc)を引数にしてmod(modelの略)に代入します
# 学習器を用意
mod = Model(desc)
fit()|学習を実行
- 学習(あるいは分析)に使用するデータを(今回はdata)を引数にして、結果はres(resultの略)に代入します
# 学習結果をresに代入する
res = mod.fit(data)
# 学習結果を表示する
print(res)
# 期待される実行結果
Name of objective: MLW
Optimization method: SLSQP
Optimization successful.
Optimization terminated successfully.
Objective value: 0.508
Number of iterations: 52
Params: 2.180 1.819 1.257 1.058 1.265 1.186 1.280 1.266 1.482 0.572 0.838 0.624 1.893 1.320 2.156 7.385 0.793 5.067 0.347 3.148 1.357 4.954 3.430 3.951 0.172 0.120 0.082 2.352 3.256 0.467 0.448
正しく実行できました
5. 学習結果を評価する
insepect()|パラメーターの推定値を調べる
# 学習結果のパラメータ一覧を表示する
inspect = mod.inspect()
print(inspect)
# 期待される実行結果
lval op rval Estimate Std. Err z-value p-value
0 dem60 ~ ind60 1.482379 0.399024 3.71502 0.00020319
1 dem65 ~ ind60 0.571912 0.221383 2.58336 0.00978421
2 dem65 ~ dem60 0.837574 0.0984456 8.50799 0
3 x1 ~ ind60 1.000000 - - -
4 x2 ~ ind60 2.180494 0.138565 15.7363 0
5 x3 ~ ind60 1.818546 0.151993 11.9646 0
6 y1 ~ dem60 1.000000 - - -
7 y2 ~ dem60 1.256819 0.182687 6.87965 6.00009e-12
8 y3 ~ dem60 1.058174 0.151521 6.9837 2.87503e-12
9 y4 ~ dem60 1.265186 0.145151 8.71634 0
10 y5 ~ dem65 1.000000 - - -
11 y6 ~ dem65 1.185743 0.168908 7.02003 2.21823e-12
12 y7 ~ dem65 1.279717 0.159996 7.99841 1.33227e-15
13 y8 ~ dem65 1.266084 0.158238 8.00114 1.33227e-15
14 dem60 ~~ dem60 3.950849 0.920451 4.2923 1.76835e-05
15 dem65 ~~ dem65 0.172210 0.214861 0.801494 0.422846
16 ind60 ~~ ind60 0.448321 0.0866766 5.17234 2.31175e-07
17 y1 ~~ y5 0.624423 0.358435 1.74208 0.0814939
18 y1 ~~ y1 1.892743 0.44456 4.25756 2.06666e-05
19 y2 ~~ y4 1.319589 0.70268 1.87794 0.0603898
20 y2 ~~ y6 2.156164 0.734155 2.93693 0.00331475
21 y2 ~~ y2 7.385292 1.37567 5.3685 7.93938e-08
22 y3 ~~ y7 0.793329 0.607642 1.30558 0.191694
23 y3 ~~ y3 5.066628 0.951722 5.32365 1.01708e-07
24 y4 ~~ y8 0.347222 0.442234 0.785154 0.432363
25 y4 ~~ y4 3.147911 0.738841 4.2606 2.03874e-05
26 y6 ~~ y8 1.357037 0.5685 2.38705 0.0169843
27 y6 ~~ y6 4.954364 0.914284 5.41884 5.9986e-08
28 y7 ~~ y7 3.430032 0.712732 4.81251 1.49045e-06
29 x2 ~~ x2 0.119894 0.0697474 1.71897 0.0856192
30 x1 ~~ x1 0.081573 0.0194949 4.18432 2.86025e-05
31 y5 ~~ y5 2.351910 0.480369 4.89604 9.77851e-07
32 y8 ~~ y8 3.256389 0.69504 4.68518 2.79711e-06
33 x3 ~~ x3 0.466732 0.0901676 5.17628 2.26359e-07
calc_stats()|適合度を表示する
# 適合度を表示する
stats = semopy.calc_stats(mod)
print(stats)
# 期待される実行結果
DoF DoF Baseline chi2 chi2 p-value chi2 Baseline CFI \
Value 35 55 38.125446 0.329171 730.654577 0.995374
GFI AGFI NFI TLI RMSEA AIC BIC \
Value 0.94782 0.918003 0.94782 0.992731 0.034738 60.983321 132.825453
LogLik
Value 0.508339
# 見づらいので、転置する
print(stats.T)
Value
DoF 35.000000
DoF Baseline 55.000000
chi2 38.125446
chi2 p-value 0.329171
chi2 Baseline 730.654577
CFI 0.995374
GFI 0.947820
AGFI 0.918003
NFI 0.947820
TLI 0.992731
RMSEA 0.034738
AIC 60.983321
BIC 132.825453
LogLik 0.508339
- サンプルデータなので、解釈は割愛します
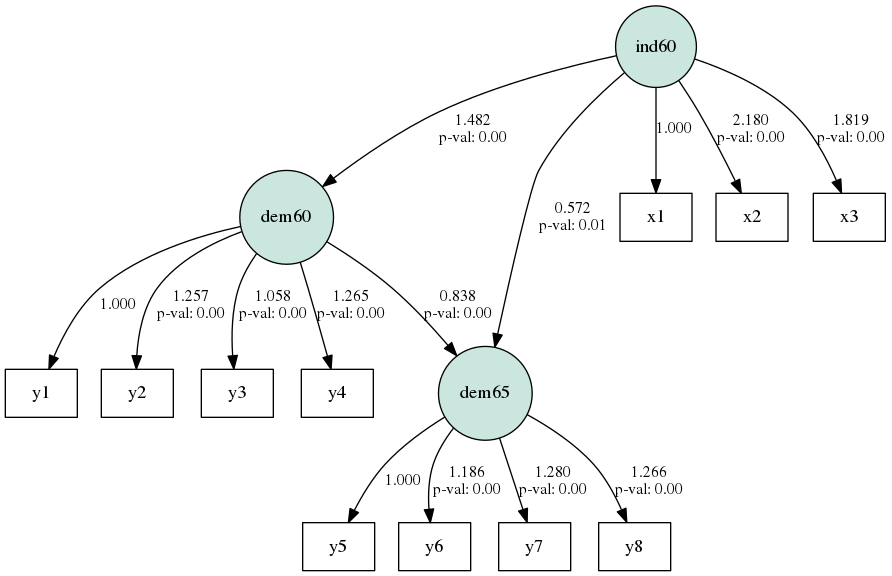
6. パス図を出力する
- シンプルな棒グラフや散布図であれば、
Matplotlibでいいのですが、パス図はノードとエッジからなるグラフです。 - そのため、Graphvizをインポートして、パス図を出力します。
Graphvizをインストール
pipコマンドの例
$ pip install graphviz
semplot()|パス図を出力する
- semplotは第一引数に利用するモデルを指定し(今回はmod)、第二引数に出力するファイル名を指定します
g = semopy.semplot(m, "sample.png")
g
共分散も表示する
- 引数に、
plot_covs=Trueをとると、共分散関係の矢印も点線でプロットされます
g = semopy.semplot(m, "sample.png", plot_covs=True)
レイアウトを変える
- 引数に、
engine="circo"をとると、図示方法がサークル型(円型)に変わります - デフォルトは
engine="dot"の階層型です
g = semopy.semplot(mod, "sample.png", plot_covs=True, engine="circo")
レイアウトの種類
- Graphvizとdot言語でグラフを描く方法のまとめ - Qiitaを参考にさせていただきました
| layout | description |
|---|---|
| circo | 円形のグラフ |
| dot | 階層型のグラフ. 有向グラフ向き. デフォルトのレイアウトエンジン |
| fdp | スプリング(ばね)モデルのグラフ. 無向グラフ向き. |
| neato | スプリング(ばね)モデルのグラフ. 無向グラフ向き. |
| osage | 配列型のグラフ. |
| sfdp | fdpのマルチスケール版. 大きな無向グラフ向き. |
| twopi | 放射型のグラフ. ノードは同心円状に配置される. |
所感
- これは一番乗りだろうと思い、semopyをいじってみると、すでにPythonで構造方程式モデリング (SEM) 〜semopyのチュートリアルを試してみる〜 - Qiitaという記事があり、先に実践していた方がいらっしゃいました
- 上記の記事もとても参考になりました。
- パス図については誤差変数が出力されない点がまだ解決されておらず、描画機能は以前Rのほうが強い印象です。
- 上記は、semopyのドキュメントを見ると解決策があるかもしれません。
- Pythonで構造方程式モデリング(SEM)をやってみよう!という人の参考になれば嬉しいです。
おわり