なかなか面白いQAOAを思いついて「これは大発見だ!」と思ったら、既にNASAやProtainQureがやっていたので、解説書きます。
QAOA
量子アニーリングのようなことをVQEと似た方法でやる量子アルゴリズムです。
Rigetti Groveのドキュメントが最も分かりやすいと思います。
https://grove-docs.readthedocs.io/en/latest/qaoa.html
要するに。
イジングモデルのハミルトニアン ($s_i \in \{\pm 1\}$)
$$
H = \sum_{i<j} J_{ij}s_i s_j + \sum_{i} h_i s_i
$$
は、量子コンピュータ上では、ZZ相互作用
$$
H = \sum_{i<j} J_{ij}\sigma^z_i \sigma^z_j + \sum_{i} h_i \sigma^z_i
$$
で書き表すことができます。
また、量子アニーリングで使う横磁場はX方向の作用 $\sigma^x$ で書き表せます。
量子アニーリングをゲート方式で真面目にシミュレーションしようと思うと、トロッター展開をして時間発展をすることになります。こちらの記事で、それを実際にやっている方がいます。
一方で、回路をできるだけ短くしたい場合、時間発展だと回路が長くなりすぎてあまりよくありません。
そこで、QAOAは、VQEのようにパラメータをつけながら、ZZ相互作用と横磁場を何度か繰り返し計算し、パラメータの最適化を行うことで、回路を短く保ったまま量子アニーリングと似たような結果を得ます。
最適化項と制約項
イジングモデルで解ける問題は、QUBOで解ける問題と等価です。
QUBOとは、Quadratic Unconstrained Binary Optimizationの略で、
$$
H = \sum_{i,j} Q_{ij}q_i q_j
$$
ただし $q_i \in \{ 0, 1\}$の形式で書き表します。
Hを最小化する、というのがQUBO問題なのですが、QUBO問題には制約条件はありません。
これは、とても不便なことです。
例えば、AランチとBランチがあって、より安いものを食べたい、という最適化問題を考えましょう。
| メニュー | 価格 |
|---|---|
| Aランチ | 800円 |
| Bランチ | 650円 |
Aランチを$q_1$, Bランチを$q_2$とすると、最適化項は
$$
H = 800 q_1 q_1 + 650 q_2 q_2
$$
となります。
Aランチを選んだ場合、$H = 800$、Bランチを選んだ場合、$H=650$となりますね。
けれど、これを最適化すると$q_1 = q_2 = 0$のとき、$H=0$となり最小になってしまいます。
どちらかを選ぶ、という問題にしたいのに「何も食べないのが一番安い」という答えが出てしまいます。
それでは困るので「制約項」を付けて、制約条件を満たさない場合にはペナルティがかかるようにします。
$$
H_{penalty} = (q_1 + q_2 - 1)^2
$$
を足し合わせて、
$$
H = 800 q_1 q_1 + 650 q_2 q_2 + \lambda H_{penalty}
$$
のようにすることで、制約条件つきのQUBOを作ることができます。
(ここで$\lambda$は、制約条件を破らなくなる程度に大きい定数です)
SWAP相互作用
現在、実用化されている量子アニーリングマシンでは、ZZ相互作用とX方向の横磁場しかかけられないのですが、量子ゲート方式だと、この制約はありません。
それを利用してVanQverアルゴリズムなどが提案されていたりします。
その他の面白い用法として、SWAP相互作用があります。
SWAP相互作用を使えば、ある種の制約項を量子回路に組み込むことができ、最適化のための条件をシンプルに保ち、制約条件を破らなくするための定数の調整もする必要がなくなります。
SWAPゲート
SWAPゲートは、2つの量子ビットを入れ替える演算で
SWAP = \begin{pmatrix}
1 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 1
\end{pmatrix}
と書けます。
|00>, |11>がそのまま、|01>と|10>が入れ替わるようになっていることが確認できます。
これは、パウリ行列で書くと
$$
SWAP = (I + \sigma^x_1 \sigma^x_2 + \sigma^y_1 \sigma^y_2 + \sigma^z_1 \sigma^z_2)/2
$$
と書けます。
あるいは、今注目しているのは|01>と|10>の入れ替えなので、
$$
SWAP' = (\sigma^x_1 \sigma^x_2 + \sigma^y_1 \sigma^y_2)/2
$$
とおくと、
SWAP' = \begin{pmatrix}
0 & 0 & 0 & 0 \\
0 & 0 & 1 & 0 \\
0 & 1 & 0 & 0 \\
0 & 0 & 0 & 0
\end{pmatrix}
となります。
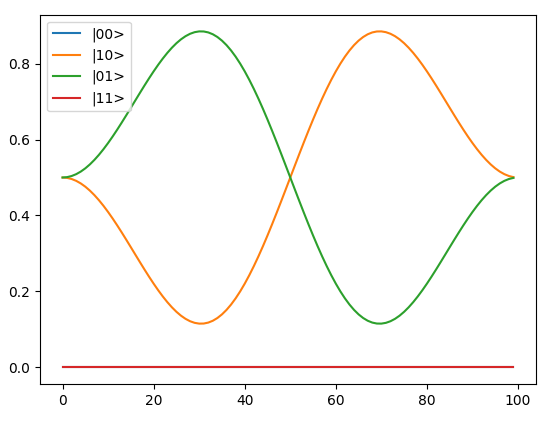
この行列の時間発展を行うと、|01>と|10>とが交互に入れ替わる形の時間発展が起こり、制約項により|00>や|11>を省く必要がなくなります。
実際にやってみた
使用したコードはこちら。Blueqatで作成しています。
from blueqat import Circuit, pauli, vqe
from blueqat.pauli import qubo_bit as q
from math import pi
import numpy as np
def an(index):
return 0.5 * pauli.X[index] + 0.5j * pauli.Y[index]
def cr(index):
return 0.5 * pauli.X[index] - 0.5j * pauli.Y[index]
op = (cr(1) * an(0) + cr(0) * an(1)).to_expr().simplify()
print(op)
x = []
y00 = []
y01 = []
y10 = []
y11 = []
evos = [term.get_time_evolution() for term in op.terms]
for i in range(100):
c = Circuit().h[0].cx[0, 1].x[1]
for evo in evos:
evo(c, i / 100 * pi)
c.rz(i / 100 * pi)[1]
for evo in evos:
evo(c, i / 100 * pi)
c.rz(i / 100 * pi)[1]
state = c.run()
_a, _b, _c, _d = list(np.abs(state) ** 2)
x.append(i)
y00.append(_a)
y10.append(_b)
y01.append(_c)
y11.append(_d)
import matplotlib.pyplot as plt
plt.plot(x, y00, label='|00>')
plt.plot(x, y10, label='|10>')
plt.plot(x, y01, label='|01>')
plt.plot(x, y11, label='|11>')
plt.legend()
plt.show()
まとめ
今回、SWAPの時間発展で|10>と|01>を入れ替えることができるのを見ました。
せっかく思いついたものが、先に誰かに見つけられていたのは残念ですが、このように量子状態に制約をつけて、望む形に操作する、というのは今後も重要になっていくと思うので、引き続き面白い応用がないか探っていきます。