はじめに
Cirq 関連の記事を書くために、面白そうなアルゴリズムを探していたところ、10月に 1Qbit から NISQ (Noisy Intermediate-Scale Quantum) に最適化した新しいアルゴリズムが発表されていたので、そちらの紹介をしたいと思います。
1Qbit について
従業員数: 50?
設立: 2012年12月1日
本部: カナダ バンクーバー
URL: https://1qbit.com/
量子コンピューティングの会社です。アクセンチャアや富士通などの大手のベンダーと提携していて量子コンピューティング会社としてはかなり有名です。1Qbit 内には日本の研究者もおり、日本の大学と共同研究も行っているみたいです。
※ この論文の著者の松浦さんは西森研のセミナーで一度お会いしました。
論文のタイトル
VanQver: The Variational and Adiabatically Navigated Quantum Eigensolver
著者: Shunji Matsuura, Takeshi Yamazaki, Valentin Senicourt, and Arman Zaribafiya
URL: https://arxiv.org/abs/1810.11511
VanQver の特徴
VanQver は量子化学計算や組み合わせ最適化問題に利用できるアルゴリズムで、一番の特徴は、以下の2つの計算方法を組み合わせて、 NISQ デバイスでも効率よく計算できるようにチューニングした点にあります。
- VQE (Variational Quantum Eigensolver) (参考文献1)
- ナビゲーターハミルトニアンを加えた AQC (Adiabatic Quantum Computation)
論文内では、VanQver と通常の AQC でのアニーリング時間の比較及び、簡単な分子の基底状態のエネルギーを厳密解と比較しています。
※ アルゴリズムの名前が会社の所在地と同じなのはオシャレですね。弊社の場合は ToQyo とかですかね。。。
VanQver の概要
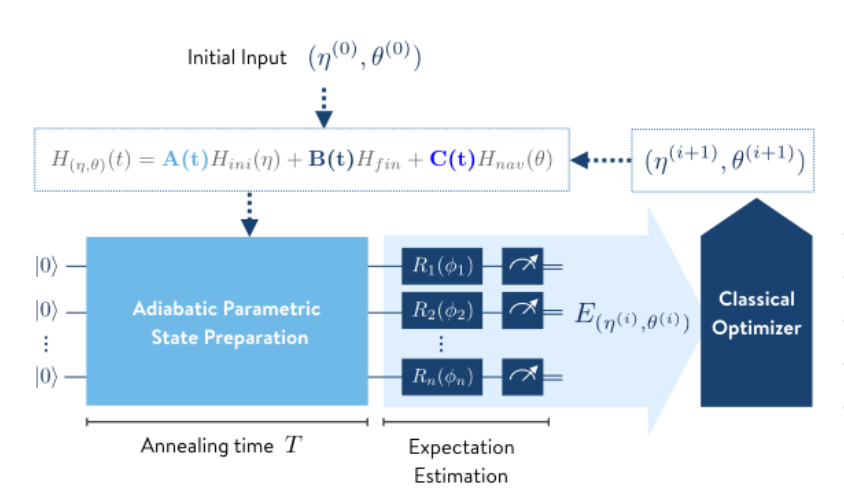
VanQver では以下のハミルトニアンを使用します。
H_{\left(\boldsymbol{\eta},\boldsymbol{\theta}\right)}\left( t \right) = A(t)\,H_{initial}(\boldsymbol{\eta}) + B(t)\,H_{final} + C(t)\,H_{navigator}(\boldsymbol{\theta})
ここで、変分パラメータ $\boldsymbol{\eta}, \boldsymbol{\theta}$ として導入し、各ハミルトニアンの係数は以下の境界条件を課しています。
\begin{align}
A(0) &= 1,\, B(0) = 0,\, C(0) = 0 \\
A(T) &= 0,\, B(T) = 1,\, C(T) = 0
\end{align}
※ $C(t)$ は境界条件で 0 になりますが、 $0 \lt t \lt T $ で 0 でない値を取るように設定します。
一番の肝になるところが、 $H_{navigator}(\boldsymbol{\theta})$ の項です。変分パラメータの $\boldsymbol{\eta}, \boldsymbol{\theta}$ をチューニングすることで、この項が AQC を実行する際にアニーリング時間 (量子コンピュータを使用して計算している時間) を最小するような計算経路を取ることを可能にします。
アルゴリズムの詳細
1 時間依存の項 $A(t),, B(t),, C(t)$ 及び $H_{ini}$、$H_{nav}$ を決定する。
2 アニーリング時間 $T$ を設定し、変分パラメータ $\boldsymbol{\eta},, \boldsymbol{\theta} $ の初期値を指定する。
3 VQE の試行関数を以下のように設定する。
\mid \psi (T)\rangle = exp\left(-i \int_{0}^{T} dt H_{\left(\boldsymbol{\eta},\boldsymbol{\theta}\right)}\left( t \right)\right) \mid \psi (0)\rangle
4 エネルギー $E\left(\boldsymbol{\eta},\boldsymbol{\theta}\right)= \langle \psi (T) \mid H_{fin} \mid \psi (T) \rangle$ を計算する
5 変分パラメータ $\left(E, \boldsymbol{\eta},\boldsymbol{\theta}\right)$ を古典コンピュータに送り、最適化計算から新たな変分パラメータ $\left(\tilde{\boldsymbol{\eta}},\tilde{\boldsymbol{\theta}}\right)$ を生成する。
6 変分パラメータ $\left(\tilde{\boldsymbol{\eta}},\tilde{\boldsymbol{\theta}}\right)$を量子コンピュータに送る。
7 3から6のステップをエネルギー $E$ が収束するまで繰り返す。
8 エネルギー $E$ を出力する。
VanQver の数値計算結果
論文にはハミルトニアンや時間に依存する係数部分を求めたい分子の基底状態に合わせて設定していますので、詳しい数式が知りたい方は論文の確認をお願いします。
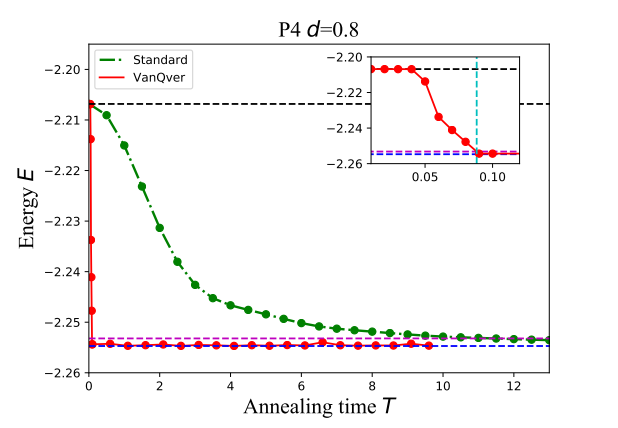
VanQver と AQC の比較
青い線が厳密解でアニーリング時間が VanQver のほうが AQC より短く、厳密解に到達している様子がわかります。だいたい $T = 0.1$で厳密解とほぼ同じになっていますね。
$T=0.1$ で複数回アニーリングを行うことになるので計算にかかる時間の合計は AQC よりも VanQver のほうが長くなる可能性はありますが、コヒーレント時間の短い NISQ デバイスでは有効かもしれないですね。
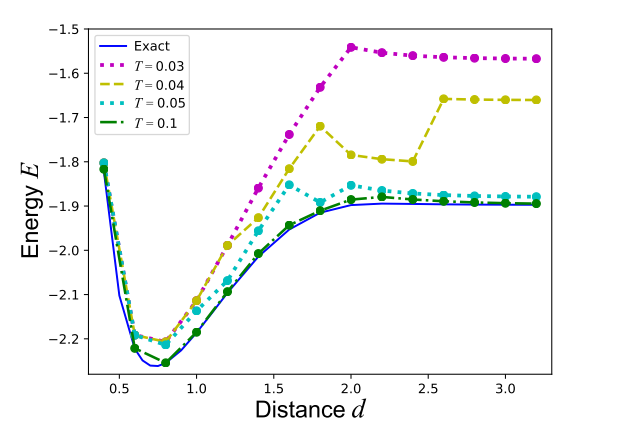
VanQver と厳密解の比較
こちらは、VanQver で計算したエネルギーと厳密解との比較になります。アニーリング時間 $T=0.1$ にすると厳密解とほぼ同じ値を取るようになるので、簡単な分子に関しては、正しい計算結果を与えるようです。
まとめ
1Qbit が開発した VanQver を紹介しました。 VanQver は特にハミルトニアンの形に依存していないアルゴリズムのため、量子化学計算だけでなく、組み合わせ最適化問題にも適応できそうです。
実際に、量子アニーリングで現在研究されている Non-Stoquastic AQC では、通常の AQC のハミルトニアンに反強磁性の項を加える研究 (参考文献2) がされています。
H_{nav} = N \left( \sum_{i=1}^{N} \sigma^{x}_{i} \right)^{2}
この項を取り入れることで指数関数的に速度向上が見られると報告されていますが、どのようなパラメータで上記の項を取り入れればよいかは、シュレディンガー方程式を解かなければ、わからなかったのですが、今回の VanQver を利用すれば、自動で最適なパラメータを探すことができそうですね。
※ 別日に Cirq を使用して組み合わせ最適化問題に VanQver を利用してみたいと思います。
また、量子コンピュータでの最適化計算は QAOA (参考文献3) もあります。QAOA の試行関数は個人的には不自然な印象を感じましたが、 VanQver では時間発展演算子を初期状態に作用させて試行関数を作成している点は物理的に自然な印象を受けました。
以上