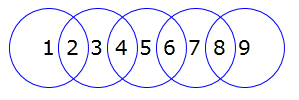
問題
以下のような5つの円に1-9までの数を入れ、どの円の中も合計すると同じ数になるように、数を埋めるというパズルです。左右の円は2つの合計、それ以外は3つの合計です。
「小町リング」というのは、僕が勝手に命名したものです。本当の名前はわかりません。
このパズルを、手計算でやろうとすると、解を一だけ見つけるのも結構大変だと思います。興味のある方はチャレンジしてください。
これを、プログラムで求めようというわけです。
単に1から9までの順列をすべて求めて、それぞれの合計を求めるのが一番手っ取り早いのですが、ここでは、順列を求めている途中で、条件にあっているかどうかを調べ、枝刈りを行っています。これにより効率的に解を求めることができるようになります。
コードの簡易解説
C#のコードと照らし合わせながら読んでほしいのですが、このプログラムの中心的な部分が、Solverクラスの_Solveメソッドです。このメソッドでは、1~9までの順列を求めながら、条件にあっているかどうかを調べています。
順列の求め方は、「C#:全ての要素を使った順列を求める」で示した方法ではなく、もっと素人っぽいやり方を取っています。numsというリストを用意し、そこに 数を追加する際に、すでに入っている数ならば除外し、入っていなければ追加する。numの要素数が 9 になったら、一つの順列が求まったので、IsRightメソッドを呼び出し、条件に一致しているかどうかを調べています。
いちいちリストの中にあるかどうかを調べているので若干効率は悪いですが、その効率の悪さをカバーしているのが、IsRighrメソッドによる枝刈りです。
IsRightメソッドはnumsに数が途中までしか入っていない状態でも、調べるこどができるようになっています。
例えば、1,2,3,4まで求まれば、1+2 ≠ 2+3+4 で条件を満たさないことが分かるので、5桁目以降は調べる必要はありません。
_Solveの最初に行っている IsRightメソッドによる判断がこれに当たります。
Mainメソッドでは、この結果を IEnumerable<int[]>で受け取り、それぞれの解を表示しています。
なお、鏡像的解は除いていませんので、これを除こうとするともう少し工夫が必要です。
以下に、C#のコードを示します。
C#のコード
using System;
using System.Linq;
namespace KomachiRing {
class Program {
static void Main(string[] args) {
Solver solver = new Solver();
foreach (var ans in solver.Solve()) {
var s = ans.Aggregate("", (r, n) => r + $"[{n}] ");
Console.WriteLine(s);
}
}
}
}
using System;
using System.Collections.Generic;
using System.Linq;
namespace KomachiRing {
public class Solver {
public IEnumerable<int[]> Solve() {
// nums は、_Solveの作業用領域
var nums = new List<int>();
return _Solve(nums);
}
// バックトラックにより、解を求める。
private IEnumerable<int[]> _Solve(List<int> nums) {
if (IsRight(nums)) {
if (nums.Count() == 9) {
// 解が求まった
yield return nums.ToArray();
} else {
for (int i = 1; i <= 9; i++) {
if (nums.Contains(i))
continue;
// i をリストに入れて試す
nums.Add(i);
// _Solveを再帰的に呼び出す。
foreach (var ans in _Solve(nums))
yield return ans.ToArray();
// 次のiを試すために、iをリストから削除する。
nums.Remove(i);
}
}
}
// 現在のnumsでの試行が終了した。
}
// 9つ揃っていなくても、途中までを判断する。
// 完全な誤りならば、falseを返す。そうでないならば、trueを返す
// 例えば、[4, 9, 1]というリストは、まだ間違いとは言えないので、trueが返る。
// これを元に枝刈りをする。
private bool IsRight(List<int> nums) {
var ite = GetSums(nums).GetEnumerator();
if (!ite.MoveNext())
// まだ、海のものとも山のものともわからない。次を調べる必要があるから、trueを返す。
return true;
int sum = ite.Current;
while (ite.MoveNext()) {
if (sum != ite.Current)
// 小町リングになっていない
return false;
}
// 現時点で、小町リングになっている
return true;
}
// numsの値をもとに、各リング内の合計を求める。
// nums.Length ==9 ならば、5つの値(合計)が列挙される。
private IEnumerable<int> GetSums(List<int> nums) {
int length = nums.Count;
if (length < 2)
yield break;
yield return nums[0] + nums[1];
for (int i = 3; i < length; i += 2) {
yield return nums[i - 2] + nums[i - 1] + nums[i];
}
if (length == 9)
yield return nums[7] + nums[8];
}
}
}
実行結果
[4] [9] [1] [3] [8] [2] [5] [6] [7]
[5] [9] [2] [3] [4] [7] [1] [6] [8]
[7] [6] [5] [2] [3] [8] [1] [4] [9]
[7] [6] [5] [2] [8] [3] [1] [9] [4]
[8] [3] [7] [1] [6] [4] [5] [2] [9]
[8] [6] [1] [7] [4] [3] [2] [9] [5]
[9] [2] [5] [4] [6] [1] [7] [3] [8]
[9] [4] [1] [8] [3] [2] [5] [6] [7]
全部で8つの解が求まりました。
この記事は、Gushwell's C# Programming Pageで公開したものをに加筆・修正したものです。