協力最短詰めオセロとは
協力最短詰めオセロとは、黒と白のプレイヤーが二人で協力して、番面の石を黒か白一色にする最短の手順を求めるパズルです。
石の初期状態と石を裏返すルールはオセロのルールをそのまま採用します。
どうやって解くか
ここでは、解を探索するのに幅優先探索のアルゴリズムを採用し、盤面の石がすべて同じ色になるまで、すべての手を試していきます。幅優先探索なので、最短手を見つけた時点で探索を終わらせることができます。深さ優先だと全ての探索をしないと最適解がわからないですからね。
クラスは、以下の6つです。
-
Program: プログラムを制御するクラス。結果表示も担当。 -
Solver: 問題を解くクラス。これがこのプログラムの中心的クラス -
Stone: 石を表すクラス -
Move: 手(どこに何色の石を置いたか)を表すクラス -
OthBoard: オセロ盤クラス(BoardBase<T>から派生) -
BoardBase<T>: 盤面クラス(汎用の基底クラス)-- ページ最後に掲載
ちょっと苦労したのは、このパズルはプレイヤーが2人いること。
最初はPlayerクラスを作ろうかとも思ったのですが、そうせずに、Solverクラスで両方の石の手を置くようにしています。
盤面を扱うOthBoardクラスの中に、石を置くPutメソッドがあるのですが、その中で次に置く石の色(白か黒か)を求めています。求めた石の色はTurnプロパティの値として設定しています。
もうすこししっかりと分析すれば、クラス設計が変わってきそうなきがします。そもそも「二人で協力して」という問題の趣旨とは完全に実装が違ってますからね。
具体的に何をやっているかは、コードに書いてあるコメントを読んでいただければと思います。
C#のコード
Program.cs
プログラムのエントリポイントであるMainが定義してあります。Solverクラスで解を求め、結果(棋譜)を表示した後に、その棋譜を画面上で再現しています。
using System;
using System.Collections.Generic;
namespace CooperatedOthello {
class Program {
static void Main(string[] args) {
var board = new OthBoard();
var sol = new Solver();
var moves = sol.Solve(board);
// 結果の棋譜を表示
foreach (var move in moves) {
var (x, y) = board.ToLocation(move.Place);
Console.WriteLine($"{move.Stone.Value} ({x}, {y})");
}
Console.WriteLine("Enterキーを押してください。");
Console.ReadLine();
// 棋譜を再現
Replay(moves);
}
// 棋譜を再現
private static void Replay(IEnumerable<Move> moves) {
var board = new OthBoard();
board.Print();
Console.ReadLine();
foreach (var move in moves) {
Console.SetCursorPosition(0, 0);
board.Put(move.Stone, move.Place);
board.Print();
Console.ReadLine();
}
}
}
}
Solver.cs
幅優先探索で解を求めています。盤面の状態をスタックに記憶しているのです。幅優先探索を書いていつも思うのが、状態をスタックに積んでいくという操作が面倒たということ、もっと簡単な方法がないのかなー。
using System;
using System.Collections.Generic;
namespace CooperatedOthello {
public class Solver {
// 幅優先探索で調べる
public IEnumerable<Move> Solve(OthBoard board) {
// 最初はどこに打っても同じなので、ひとつに固定。
int p = board.ToIndex(3, 4);
board.Put(board.Turn, p);
var queu = new Queue<OthBoard>();
queu.Enqueue(new OthBoard(board));
var current = board;
while (queu.Count != 0) {
//キューの先頭からノード currentNode を取り出す
current = queu.Dequeue();
if ((current.StoneCount(Stone.Black) == 0) ||
(current.StoneCount(Stone.White) == 0)) {
// 解がひとつ見つかれば終了。その手順を返す。
return current.GetMoves();
}
foreach (var pos in current.PutablePlaces(current.Turn)) {
var next = new OthBoard(current);
next.Put(next.Turn, pos);
// 試した手の状態はキューに入れる
queu.Enqueue(next);
}
}
// 見つからなかった
return new Move[0];
}
}
}
OthBoard.cs
Stone, Move, OthBoardの3つのクラスを定義
オセロの盤面を表すクラスOthBoardは、BrardBase<T>クラス(ページ最後に掲載)を継承して作成しています。
using Puzzle;
using System;
using System.Collections.Generic;
using System.Linq;
// Boardから継承し、特有の機能を追加
namespace CooperatedOthello {
public class Stone {
public static readonly Stone Black = new Stone { Value = 'X' };
public static readonly Stone White = new Stone { Value = 'O' };
public static readonly Stone Empty = new Stone { Value = '.' };
public char Value { get; set; }
}
public class Move {
public int Place { get; set; }
public Stone Stone { get; set; }
public Move(Stone stone, int place) {
Stone = stone;
Place = place;
}
}
public class OthBoard : BoardBase<Stone> {
// 現在の手番の事。
public Stone Turn { get; set; }
// これまでの棋譜
private List<Move> Moves = new List<Move>();
// コンストラクタ
public OthBoard()
: base(8, 8) {
Turn = Stone.Black;
Initialize();
}
// コンストラクタ (Cloneと同じ用途)
public OthBoard(OthBoard board)
: base(board) {
Turn = board.Turn;
Moves = board.Moves.ToList();
}
// 初期化
public void Initialize() {
foreach (var p in GetAllIndexes())
this[p] = Stone.Empty;
this[ToIndex(4, 4)] = Stone.White;
this[ToIndex(5, 5)] = Stone.White;
this[ToIndex(4, 5)] = Stone.Black;
this[ToIndex(5, 4)] = Stone.Black;
}
// 相手の石
public Stone Opponent(Stone stone) {
return stone == Stone.White ? Stone.Black : Stone.White;
}
// 石の数をカウント
public int StoneCount(Stone stone) {
return this.GetAllIndexes().Count(p => this[p] == stone);
}
// 8つの方向を列挙 (このBoardは、番兵用に一回り大きなサイズとなっている)
public IEnumerable<int> Directions() {
//return new int[] { -OuterWidth-1, -OuterWidth, -OuterWidth+1, 1, OuterWidth + 1, OuterWidth, OuterWidth-1, -1 };
return new int[] {
ToDirection(-1, -1),
ToDirection( 0, -1),
ToDirection(+1, -1),
ToDirection(+1, 0),
ToDirection(+1, +1),
ToDirection( 0, +1),
ToDirection(-1, +1),
ToDirection(-1, 0),
};
}
// 置ける場所を列挙する
public IEnumerable<int> PutablePlaces(Stone stone) {
return this.GetVacantIndexes().Where(index => CanPut(stone, index));
}
private IEnumerable<int> GetVacantIndexes() {
return this.GetAllIndexes().Where(p => this[p] == Stone.Empty);
}
// 石を置けるか
public bool CanPut(Stone stone, int place) {
if (this[place] != Stone.Empty)
return false;
return Directions().Any(d => CanReverse(stone, place, d));
}
// direction方向の石をひっくり返せるか
public bool CanReverse(Stone stone, int place, int direction) {
Stone opponent = Opponent(stone);
int np = place + direction;
while (this[np] == opponent)
np += direction;
return (this[np] == stone && np != place + direction);
}
// direction方向にstoneと同じ色の石があるか
public bool FindStone(Stone stone, int place, int direction) {
Stone opponent = Opponent(stone);
int np = place + direction;
while (this[np] == opponent)
np += direction;
return (this[np] == stone);
}
// direction方向の石をひっくり返えす
public void Reverse(Stone stone, int place, int direction) {
if (!FindStone(stone, place, direction))
return;
Stone opponent = Opponent(stone);
int np = (int)(place + direction);
while (this[np] == opponent) {
this[np] = stone;
np += direction;
}
}
// stoneをplace位置に置く (必ず置けることを前提としている)
public void Put(Stone stone, int place) {
this[place] = stone;
Stone opponent = Opponent(stone);
foreach (int direction in Directions()) {
Reverse(stone, place, direction);
}
Moves.Add(new Move(stone, place));
// 通常は相手の番になるが、相手が置ける場所が無い場合は、連続して打てる
if (PutablePlaces(Turn).Any())
Turn = opponent;
else
Turn = stone;
}
// 現時点での手順を返す。
public IEnumerable<Move> GetMoves() {
return Moves;
}
public void Print() {
Console.Clear();
for (int y = 1; y <= YSize; y++) {
for (int x = 1; x <= XSize; x++) {
Console.Write("{0} ", this[x, y].Value);
}
Console.WriteLine("");
}
Console.WriteLine();
}
}
}
実行結果
僕のコンピュータ(MacBook Pro)で約20秒ほどで解が求まりました。
ちなみに、このプログラムは、.NET Core2.1で動かしています。ソースコードは、.NET Framework + Windowsでもそのまま動くはずです。
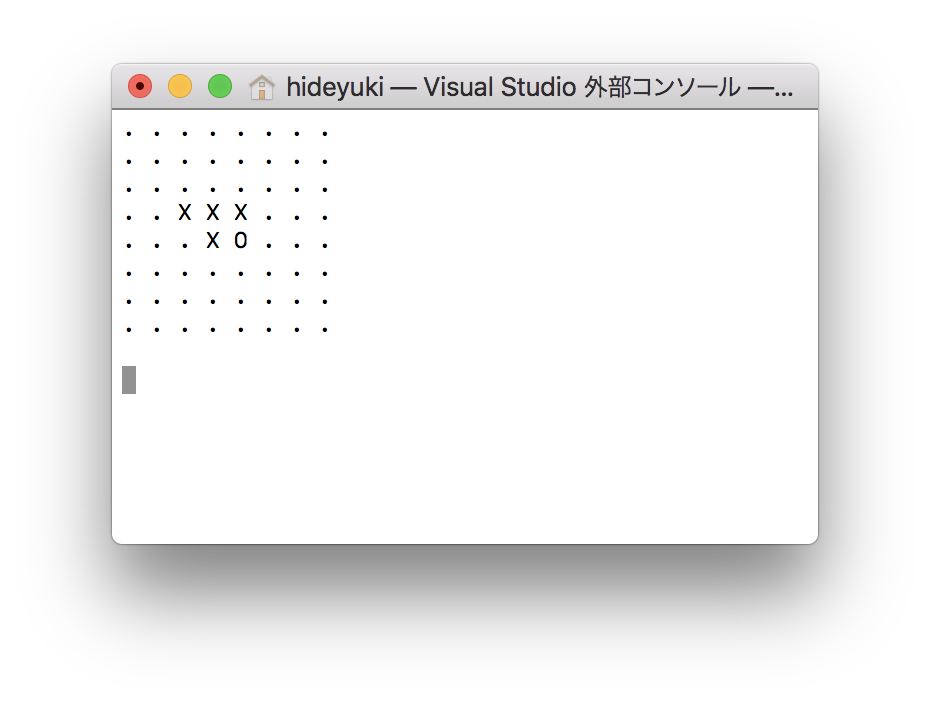
Xが黒、Oが白を表しています。
X (3, 4)
O (3, 3)
X (3, 2)
O (2, 4)
X (1, 5)
O (6, 4)
X (7, 4)
O (3, 5)
X (4, 6)
これが棋譜です。合わせて9手で盤面を一色にできることがわかります。
この後、Enterキーを押すことで、盤面の状態をひとつずつ再現します。
Console.SetCursorPosition() メソッドを使っているので、画面はスクロールせずに、最初に表示した盤面を上書きするようになっています。
以下、その一部です。
1手目
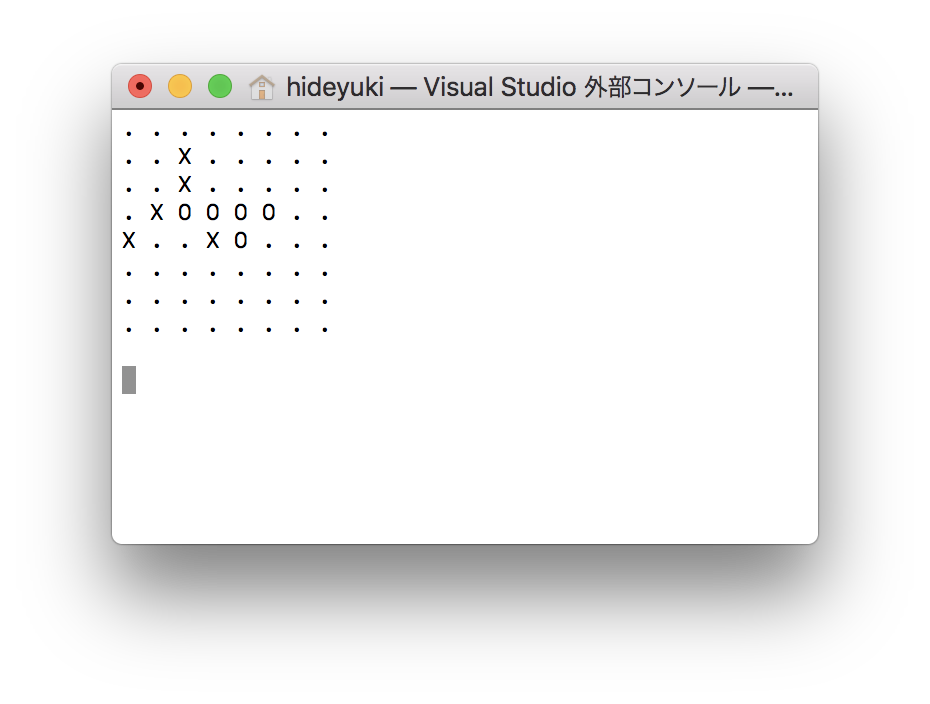
6手目
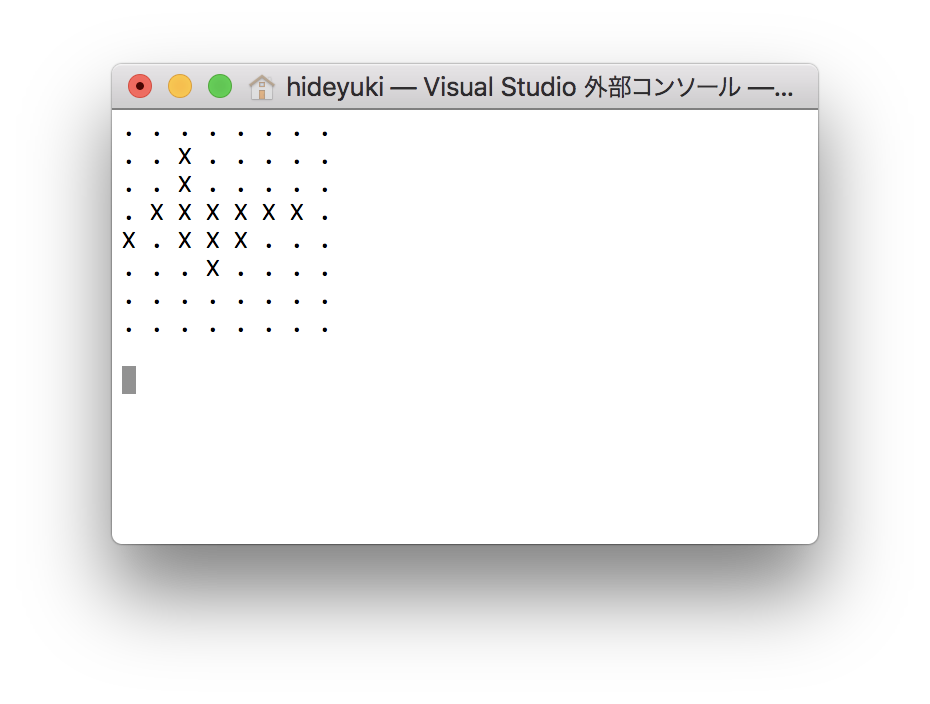
9手目
最後は、黒一色になりました。
BoardBaseクラス
このBoardBaseクラスは、「騎士巡回問題」「ナイト(騎士)の最適配置問題」などで利用したものと同じものです。
前述のBoardクラスの基底クラスです。X × Y の盤面を表し、基本的な操作を定義しています。これは似たようなパズルでも再利用できるような汎用的な機能に絞っています。このBoardBaseクラスは、コンソールアプリに依存しない作りにしています。UWP、WinFormsでもそのまま使えると思います。
このBoardBaseを継承して、当パズル専用のBoardクラスを定義します。
内部では1次元配列を使っていますが、インデクサを定義して、1次元配列、2次元配列としても扱えるようにしています。
ただし、すべてのメソッドで1次元対応と2次元対応のものを用意するのは面倒なので、どちらか一方にしています。まあこれは好み以外の何物でもありません。
1次元のインデックスによるアクセスができるようにしている理由は、一重ループで処理が書けるので、コードが簡潔になるからです。LINQのコードも書きやすくなります。
2次元配列として見た場合の、X座標、Y座標は、0 からではなく、1から始まります。
つまり、board[1,1] は、いちばん左上を示し、8×8の盤ならば、board[8,8]が右下を示すことになります。
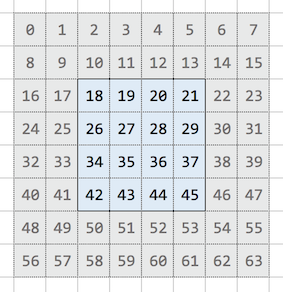
なお、盤の周りには番兵用の領域を用意しています。これにより範囲外かどうかの判断を簡単に出来るようにしています。チェスのナイト(騎士)の動きにも対応できるよう、番兵は二重にしています。
上の図は 4×4の盤を表していますが、グレー部分が番兵が置いてある盤の周囲で、水色部分が実際の盤です。
盤面上の数値は、1次元配列のインデックスを表しています。
なお、派生クラスや派生クラスを利用するクラスが、この番兵の存在に依存しないように、ToDirectionという関数を定義し、X方向、Y方向のペアで表す移動方向(ベクトル)をインデックスで表す方向に変換するようにしています。
BoardBaseクラスはジェネリッククラスにしていて、そのパラメータの型は、盤面上に置けるクラスの型です。
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
namespace Puzzle {
// 汎用の盤面クラス
// Tは、盤面に置けるオブジェクトの型。参照型でnew()ができれば何でも良い。
public abstract class BoardBase<T> where T : class, new() {
private T[] _pieces;
// 盤の行数(縦方向)
public int YSize { get; private set; }
// 盤のカラム数(横方向)
public int XSize { get; private set; }
// コンストラクタ
public BoardBase(int xsize, int ysize) {
this.YSize = ysize;
this.XSize = xsize;
_pieces = new T[(xsize + 2) * (ysize + 2)];
// 盤データの初期化 - 盤の周りはnull(番兵)をセットしておく
ClearAll();
}
// コピー用コンストラクタ
public BoardBase(BoardBase<T> board) {
XSize = board.XSize;
YSize = board.YSize;
this._pieces = board._pieces.ToArray();
}
// 番兵も含めたボード配列の長さ
public int BoardLength {
get { return _pieces.Length; }
}
// インデクサ (x,y)の位置の要素へアクセスする
public T this[int index] {
get { return _pieces[index]; }
set { _pieces[index] = value; }
}
// インデクサ (x,y)の位置の要素へアクセスする
public T this[int x, int y] {
get { return this[ToIndex(x, y)]; }
set { this[ToIndex(x, y)] = value; }
}
// Location から _coinのIndexを求める
public int ToIndex(int x, int y) => x + y * (XSize + 2);
// IndexからLocationを求める (ToIndexの逆演算)
public (int, int) ToLocation(int index) => (index % (XSize + 2), index / (XSize + 2));
// 本来のボード上の位置(index)かどうかを調べる
public virtual bool IsOnBoard(int index) {
if (0 <= index && index < BoardLength)
return this[index] != null;
return false;
}
// 全てのPieceをクリアする
public virtual void ClearAll() {
for (int index = 0; index < BoardLength; index++)
this[index] = null; // 番兵
foreach (var index in GetAllIndexes())
this[index] = new T(); // 初期値
}
// 盤上のすべての位置(index)を列挙する
public virtual IEnumerable<int> GetAllIndexes() {
for (int y = 1; y <= this.YSize; y++) {
for (int x = 1; x <= this.XSize; x++) {
yield return ToIndex(x, y);
}
}
}
// (x,y)からdirection方向の位置を列挙する (x,y)含む
public virtual IEnumerable<int> EnumerateIndexes(int x, int y, int direction) {
for (int index = ToIndex(x, y); IsOnBoard(index) && this[index] != null; index += direction)
yield return index;
}
// (x,y)から右(水平)の位置を列挙する (x,y)含む
public virtual IEnumerable<int> Horizontal(int x, int y)
=> EnumerateIndexes(x, y, 1);
// (x,y)から下(垂直)の位置を列挙する (x,y)含む
public virtual IEnumerable<int> Virtical(int x, int y)
=> EnumerateIndexes(x, y, this.XSize + 2);
// (x,y)から右斜め下(45度)の位置を列挙する (x,y)含む
public virtual IEnumerable<int> SlantR(int x, int y)
=> EnumerateIndexes(x, y, this.XSize + 2 + 1);
// (x,y)から左斜め下(45度)の位置を列挙する (x,y)含む
public virtual IEnumerable<int> SlantL(int x, int y)
=> EnumerateIndexes(x, y, this.XSize + 2 - 1);
}
}
この記事は、Gushwell's C# Programming Pageで公開したものを大幅に加筆・修正したものです。