C#でパズルを解く - 騎士巡回問題(Knight's Tour)

ナイト巡回問題とは

ナイト巡回問題とは、チェスを使った数学的パズルの一種です。チェスのナイトをチェス盤の上を動かし、すべてのマス(64)を通り最初の場所に戻ってくる経路を求めるというものです。
もしかしたら「最初の場所に戻ってくる」という制約をつけないバージョンが一般的かもしれません。

ご参考: Wikipedia ナイト・ツアー

以下に、解の一つを載せます。1から64までを線で結んでいます。

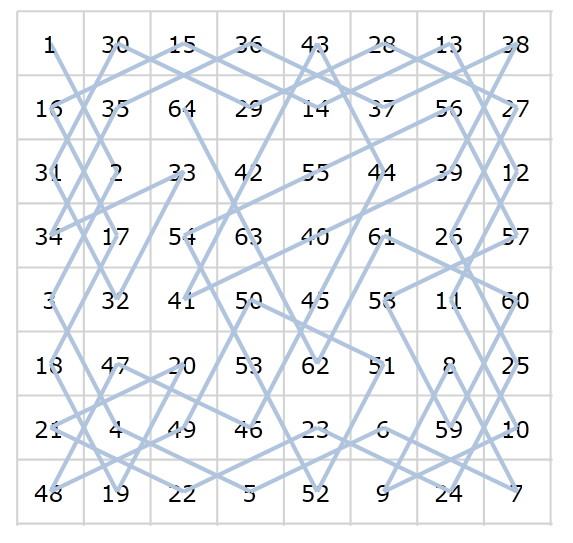
実際にはコンソールアプリで解いているので、このようなグラフィカルな表現ではありませんが...

それにしても画像がでかいなー(笑)

どうやって解くか

この問題を解くには、

8-クィーンパズル
MagicStarパズル

のように、バックトラック法を使います。

簡単に解き方を説明すると、

1. ナイトを任意の位置に置く
2. 移動できる候補に対して3-7を実行
3. 次に動かす場所がなければ、失敗->2へ
4. 巡回する前に、開始位置に戻れる場所がすべて埋まってしまったら失敗->2へ
5. すべてのマスを通り、もとに戻れる位置にいれば終了（成功）
6. 移動できる候補にナイトを移動
7. 再帰的に2からの処理を実行する

とこんな感じです。

なお、ナイトを動かした場所には、何番目に移動したかを記録する番号を振っておきます。

もちろん、失敗したときには、後戻りしないといけませんから、再帰処理でこれをやっています。
解は一つだけ求めています。

ちなみに、このプログラムでは、ナイトの開始位置を、チェスゲームのナイトの初期配置の一つ(2,1)を選んでいます。

主要なクラス

Solver クラス

解を求めるクラです。このクラス自体は、コード量も少なくそれほど複雑なことをしているわけではありません。
なお、開始位置は、Solveメソッドの第2引数の値を変えることで変更できます。

Chessboardクラス

チェス盤を表すクラスで、BoardBaseクラス(後述)を継承しています。

Solverクラスは、このChessBoardを使い、ナイトを置いたり、取り外したり、何歩目かを記録したりしています。

C#のコード

以下C#のコードです。

Programクラス

using System;

namespace KnightTourApp {
    class Program {
        static void Main(string[] args) {
            var board = new Chessboard(8);
            board.StartPlace = board.ToIndex(2, 1);
            var solver = new Solver();
            var answer = solver.Solve(board);
            answer.Print();
        }
    }
}

Solverクラス

このプログラムでは、解を一つだけ求めています。全ての解を求めたい場合は、C#でパズルを解く - バックトラッキングで8-Queenパズルを解くで示したようなやり方で、SolveInnerメソッド/Solveメソッドを変更し、IEnumerable<Chessboard>を返すようにする必要があります。

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace KnightTourApp {
    class Solver {
        private int _startPlace;
        public Chessboard Solve(Chessboard board) {
            if (board.StartPlace == 0)
                board.StartPlace = board.ToIndex(1, 1);
            _startPlace = board.StartPlace;
            return SolveInner(board, _startPlace);
        }

        private Chessboard SolveInner(Chessboard board, int nowPlace) {
            // 全ての位置に移動し、現在の位置からStart地点にジャンプできれば、解が求まった。
            if (board.IsFin()) {
                if (board.CanBackHome())
                    return board;
                return null;
            }
            // OrderBy を入れるか入れないかで、圧倒的な速度差が出る
            List<int> list = board.CanPutPlaces(nowPlace).OrderBy(n => board.CanPutPlaces(n).Count()).ToList();
            foreach (int pos in list) {
                board.Jump(pos);
                // 枝刈り用の処理：この判断が無いととてつもなく遅くなってしまう。
                if (board[pos] is Footmark fm) {
                    // 開始位置からJumpする場所が無いなら、これ以上探しても意味が無いので次の可能性へ。
                    if ((fm.Number != board.YSize * board.XSize) &&
                        (board.CanPutPlaces(_startPlace).Count() == 0)) {
                        board.Clear(pos);
                        continue;
                    }
                }
                // 枝刈り：ここまで
                var ans = SolveInner(board, pos);
                if (ans != null)
                    return ans;
                board.Clear(pos);
            }
            // ジャンプできる場所はすべて試した。解は見つからない。
            return null;
        }
    }
}

Peice/Chessboardクラス

このソースでは、3つのクラスを定義しています。
Pieceは駒クラスです。何も置いていないマスにはEmpty駒が置いてあるものとしています。

Footmarkは、足跡を示すクラスで、ナイトが通ったマスには、このFootmarkが置かれます。Numberは、何歩目かを表すプロパティです。Pieceから継承しています。Chessboardに置けるのは、Pieceオブジェクトなので、このような継承関係を持たせています。

Chessboardウラスは、そのなの通りチェス盤を表すクラスです。問題を解くための（チェス盤を操作する）各種メソッドが定義してあります。

using Puzzle;
using System;
using System.Collections.Generic;
using System.Text;
using System.Linq;

namespace KnightTourApp {

    public class Piece {
        public static readonly Piece Empty = new Piece { Value = '.' };
        public static readonly Piece Knight = new Piece { Value = 'K' };
        public char Value { get; set; }

        public override string ToString() {
            return Value.ToString();
        }
    }

    // ナイトの足跡 Numberは、何歩目なのかを示す。
    public class Footmark : Piece {
        public int Number { get; set; }
        public Footmark(int num) {
            Number = num;
        }
    }

    // チェスボードを表すクラス 
    // 描画は担当しない。あくまでも内部構造。ChessboardCanvasが描画を担当
    public class Chessboard : BoardBase<Piece> {
        private int _count = 0;
        private int _startPlace;
        private int _nowPlace;

        public Chessboard(int width) : base(width, width) {
            ClearAll();
        }

        // 開始位置を決定
        public int StartPlace {
            get { return _startPlace; }
            set {
                if (_startPlace != 0)
                    ClearAll();
                _count = 0;
                _startPlace = value;
                Jump(_startPlace);
            }
        }

        // EmptyPiece 以外の全てのPieceを列挙する

        public IEnumerable<Piece> GetAllPieces() {
            return GetAllIndexes().Select(i => this[i]).Where(p => p != Piece.Empty);

        }

        // 移動させる
        public void Jump(int place) {
            this[place] = new Footmark(++_count);

            _nowPlace = place;
        }

        // place位置をクリア (開始位置はクリアできない)
        public void Clear(int place) {
            _count = (this[place] as Footmark).Number - 1;
            this[place] = Piece.Empty;
            _nowPlace = this.GetAllPieces()
                            .OfType<Footmark>()
                            .Max(fm => fm.Number);
        }

        // 全てをクリア
        public override void ClearAll() {
            base.ClearAll();
            foreach (var p in this.GetAllIndexes())
                this[p] = Piece.Empty;
            _startPlace = 0;
        }

        // 巡回したか
        public bool IsFin() {
            return this.GetAllIndexes().All(n => this[n] is Footmark);
        }

        // Start位置に戻ってこられる状態かを調べる。
        public bool CanBackHome() {
            return Destinations(StartPlace).Any(n => {
                var piece = this[n] as Footmark;
                if (piece != null) {
                    if (piece.Number == this.XSize * this.YSize)
                        return true;
                }
                return false;
            });
        }

        // placeから実際に移動できる位置を列挙する
        public IEnumerable<int> CanPutPlaces(int place) {
            return Destinations(place).Where(n => this[n] == Piece.Empty).ToArray();
        }

        // Knightの移動候補位置を列挙する （移動先にKnightがあるかどうかは考慮しない)
        public IEnumerable<int> Destinations(int place) {
            int[] candidates = {
                ToDirection(+1, -2),
                ToDirection(+2, -1),
                ToDirection(+1, +2),
                ToDirection(+2, +1),

                ToDirection(-1, -2),
                ToDirection(-2, -1),
                ToDirection(-1, +2),
                ToDirection(-2, +1),
           };
            return candidates.Select(d => place + d).Where(ix => IsOnBoard(ix));
        }

        public void Print() {
            for (int y = 1; y <= YSize; y++) {
                for (int x = 1; x <= XSize; x++) {
                    Footmark fm = this[x, y] as Footmark;
                    if (fm != null)
                        Console.Write("{0,2} ", fm.Number);
                    else
                        Console.Write("{0}  ", this[x, y] == Piece.Knight ? "K" : " ");
                }
                Console.WriteLine("");
            }
            Console.WriteLine();
        }
    }
}

実行結果

実行結果です。

数値が騎士の巡回する順番を示しています。最後の64から初期の1の位置に移動できますから、ちゃんと巡回できているのが確認できます。

 4  1  6 21 28 33 16 19 
 7 22  3 64 17 20 29 32 
 2  5 24 27 34 31 18 15 
23  8 63 56 25 40 35 30 
62 57 26 53 44 55 14 39 
 9 52 45 60 47 38 41 36 
58 61 50 11 54 43 48 13 
51 10 59 46 49 12 37 42 

試しに、右上を開始位置にして解いてみました。大丈夫そうですね。

38 13 28 63 36 15 30  1 
27 50 37 14 29 64 35 16 
12 39 58 49 62 33  2 31 
51 26 55 40 57 42 17 34 
54 11 52 59 48 61 32  3 
25  8 47 56 41 20 43 18 
10 53  6 23 60 45  4 21 
 7 24  9 46  5 22 19 44 

BoardBaseクラス

このBoardBaseクラスは、「ナイト(騎士)の最適配置問題」などで利用したものと同じものです。

前述のBoardクラスの基底クラスです。X × Y の盤面を表し、基本的な操作を定義しています。これは似たようなパズルでも再利用できるような汎用的な機能に絞っています。このBoardBaseクラスは、コンソールアプリに依存しない作りにしています。UWP、WinFormsでもそのまま使えると思います。

このBoardBaseを継承して、当パズル専用のBoardクラスを定義します。

内部では1次元配列を使っていますが、インデクサを定義して、1次元配列、2次元配列としても扱えるようにしています。
ただし、すべてのメソッドで１次元対応と２次元対応のものを用意するのは面倒なので、どちらか一方にしています。まあこれは好み以外の何物でもありません。

１次元のインデックスによるアクセスができるようにしている理由は、一重ループで処理が書けるので、コードが簡潔になるからです。LINQのコードも書きやすくなります。

2次元配列として見た場合の、X座標、Y座標は、0 からではなく、1から始まります。
つまり、board[1,1] は、いちばん左上を示し、8×8の盤ならば、board[8,8]が右下を示すことになります。

なお、盤の周りには番兵用の領域を用意しています。これにより範囲外かどうかの判断を簡単に出来るようにしています。ナイト(騎士)の動きに対応できるよう、番兵は二重にしています。

派生クラスや派生クラスを利用するクラスが、できるだけこの番兵の存在に依存しないように、ToDirectionという関数を定義し、X方向、Y方向のペアで表す移動方向(ベクトル)をインデックスで表す方向に変換するようにしています。

上の図は 4×4の盤を表しています。グレー部分が番兵が置いてある盤の周囲で、水色部分が実際の盤です。
盤面上の数値は、１次元配列のインデックスを表しています。

BoardBaseクラスはジェネリッククラスにしていて、そのパラメータの型は、盤面上に置けるクラスの型です。

using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;

namespace Puzzle {
    // 汎用の盤面クラス
    // Tは、盤面に置けるオブジェクトの型。参照型でnew()ができれば何でも良い。
    public abstract class BoardBase<T> where T : class, new() {
        private T[] _pieces;

        // 盤の行数（縦方向）
        public int YSize { get; private set; }

        // 盤のカラム数（横方向）
        public int XSize { get; private set; }

        // 番兵も含めた幅のサイズ
        private int OuterWidth => XSize + 4;

        private int OuterHeight => XSize + 4;

        // コンストラクタ
        public BoardBase(int xsize, int ysize) {
            this.YSize = ysize;
            this.XSize = xsize;

            _pieces = new T[OuterWidth * OuterHeight];

            // 盤データの初期化 - 盤の周りはnull(番兵)をセットしておく
            ClearAll();
        }

        // コピー用コンストラクタ
        public BoardBase(BoardBase<T> board) {
            XSize = board.XSize;
            YSize = board.YSize;
            this._pieces = board._pieces.ToArray();
        }

        // 番兵も含めたボード配列の長さ
        public int BoardLength => _pieces.Length;


        // インデクサ (x,y)の位置の要素へアクセスする
        public T this[int index] {
            get { return _pieces[index]; }
            set { _pieces[index] = value; }
        }

        // インデクサ (x,y)の位置の要素へアクセスする
        public T this[int x, int y] {
            get { return this[ToIndex(x, y)]; }
            set { this[ToIndex(x, y)] = value; }
        }

        // Location から _coinのIndexを求める
        public int ToIndex(int x, int y) => x + 1 + (y + 1) * OuterWidth;

        // IndexからLocationを求める (ToIndexの逆演算)
        public (int, int) ToLocation(int index) 
            => (index % OuterWidth - 1, index / OuterWidth - 1);


        public int ToDirection(int dx, int dy) => dy * OuterWidth + dx;

        // 本来のボード上の位置(index)かどうかを調べる
        public virtual bool IsOnBoard(int index) => this[index] != null;


        // 全てのPieceをクリアする
        public virtual void ClearAll() {
            for (int index = 0; index < BoardLength; index++)
                this[index] = null;       // 番兵
            foreach (var index in GetAllIndexes())
                this[index] = new T();　　// 初期値
        }

        // 盤上のすべての位置(index)を列挙する
        public virtual IEnumerable<int> GetAllIndexes() {
            for (int y = 1; y <= this.YSize; y++) {
                for (int x = 1; x <= this.XSize; x++) {
                    yield return ToIndex(x, y);
                }
            }
        }

        // (x,y)からdirection方向の位置を列挙する　(x,y)含む
        public virtual IEnumerable<int> EnumerateIndexes(int x, int y, int direction) {
            for (int index = ToIndex(x, y); IsOnBoard(index); index += direction)
                yield return index;
        }

        // (x,y)から右(水平)の位置を列挙する　(x,y)含む
        public virtual IEnumerable<int> Horizontal(int x, int y)
            => EnumerateIndexes(x, y, ToDirection(1, 0));

        // (x,y)から下(垂直)の位置を列挙する　(x,y)含む
        public virtual IEnumerable<int> Virtical(int x, int y)
            => EnumerateIndexes(x, y, ToDirection(0, 1));

        // (x,y)から右斜め下(45度)の位置を列挙する　(x,y)含む
        public virtual IEnumerable<int> SlantR(int x, int y)
            => EnumerateIndexes(x, y, ToDirection(1, 1));

        // (x,y)から左斜め下(45度)の位置を列挙する　(x,y)含む
        public virtual IEnumerable<int> SlantL(int x, int y)
            => EnumerateIndexes(x, y, ToDirection(-1, 1));

    }
}

---

この記事は、Gushwell's C# Programming Pageで公開したものを大幅に加筆・修正したものです。