前回では
機械学習における学習とは一言で言うと
「重みを訓練データから自動的に決定する」ことです。
前回示した通り、ステップで示すと以下のようになります。
ステップ①:ある重みからなるニューラルネットワークに訓練データ[入力]を入力する。
ステップ②:ニューラルネットワークは順伝播を行い、演算結果を出力する。
ステップ③:出力したデータと教師データ（訓練データ[出力]）を比較し、損失関数を計算する。
ステップ④:損失関数を基に逆伝播を行い、勾配を計算する。
ステップ⑤:勾配方向に重みを少しだけ更新する。
①～⑤を繰り返す
繰り返した結果、訓練データの入力と出力の関係をうまく説明できる重みをもつニューラルネットワークが構築される。
さあ、それではステップごとにどのような仕組みになっているのか見ていきましょう。
前回の専門用語たちの説明も登場します。
ステップ①
まずはステップ①から見てみましょう。ステップ①は以下のようでしたね。
ステップ①:ある重みからなるニューラルネットワークに訓練データ[入力]を入力する。
最初に、ある重みからなるニューラルネットワークを定義する必要があります。
まずニューラルネットワークのモデルを決めます。形を決めます。
つまり y = ax + b みたいな式を決めたのと同じ意味合いを持ちます。
次に、重みの初期値を決めます。
つまり y = ax + b の a と b の初期値を決めて、y = 2x + 5 とするのと同じです。
重みの初期値の決め方はかなり大きなテーマですが今回は割愛します。
これで、ある重みからなるニューラルネットワークができました。
ここに訓練データ[入力]を入力します。
実際に完成したＡＩに食わせるデータです。y = ax + b でいう x にあたります。
この例では分かりやすくするために変数 x は1つですが、実践ではかなり多くの変数が必要です。
つまりＡＩに食わせるデータの種類の数だけ必要になるということです。
ＡＩに食わせるデータの種類は競馬を例にとると、馬体重や騎手の体重、
最速タイムなどが考えられます。
馬体重だけからでは勝ち馬は予想できなさそうですよね？
馬体重と騎手の体重や最速タイムなどの情報を全部変数として使えたほうが予想精度があがりそうですよね？
こういったことを考えながらニューラルネットワークのモデルを決めるのです。
モデルが決まると必然的に訓練データ[入力]のデータ構造も決まります。
入力データは馬体重と騎手の体重の2種類にしよう！みたいな感じです。
さあ、設計したニューラルネットワークに訓練データ[入力]をぶち込んで次のステップに進みましょう。
ステップ②
ステップ②:ニューラルネットワークは順伝播を行い、演算結果を出力する。
訓練データ[入力]をぶち込まれたニューラルネットワークはそれを基に計算し、
結果を出力します。
y = 2x + 5 に x = 7 をぶち込んで計算し、y = 19 を出力するのと同様です。
図に示すと以下のようになります。
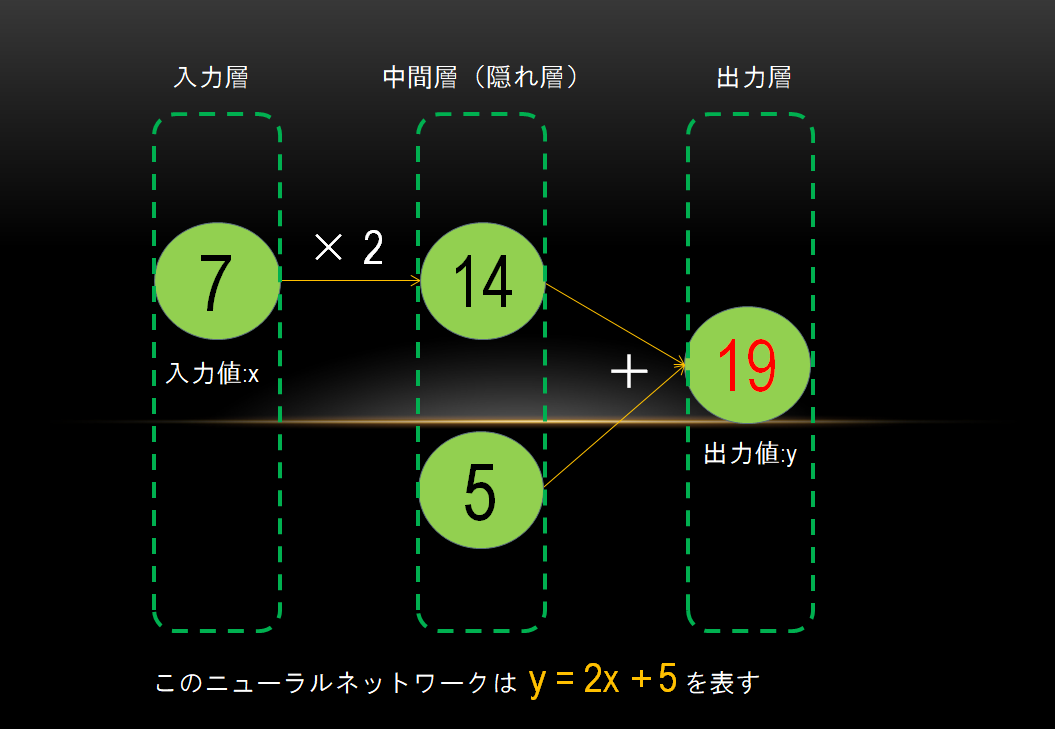
fig.1 【 y = 2x + 5 】を表すニューラルネットワーク
訓練データ[入力]をもとにニューラルネットワークが計算し、
演算結果を出力することを順伝播といいます。
順方向に計算結果が伝播していくからです。
以下に順伝播のイメージを示します。
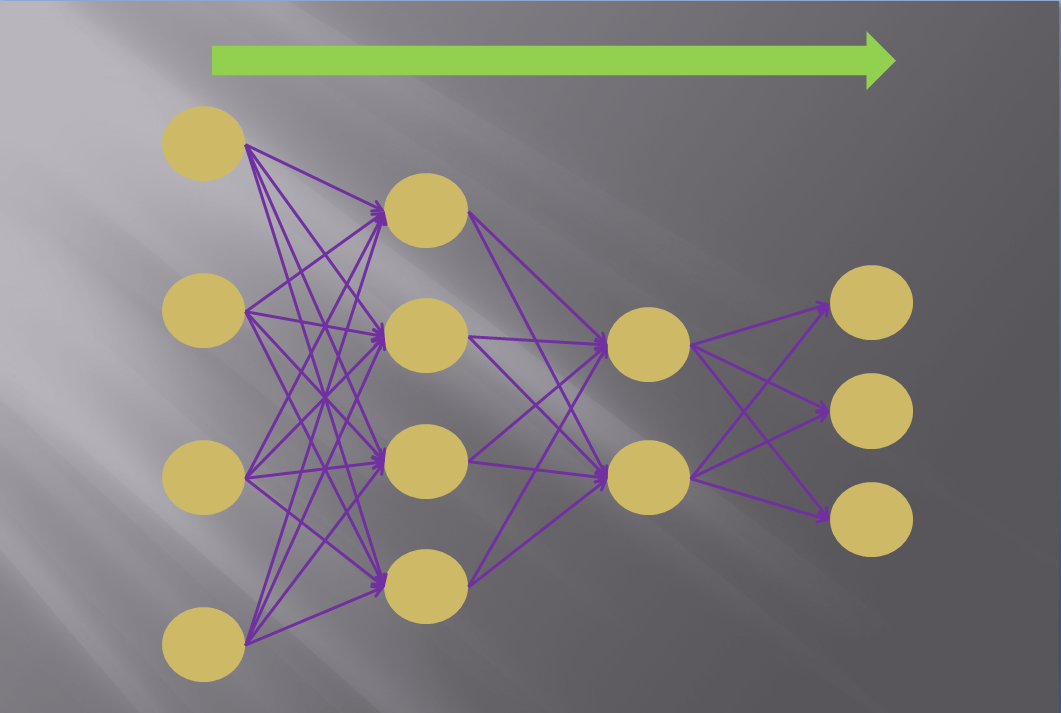
fig.2 順伝播
あなたのニューラルネットワークが訓練データ[入力]から出力結果をはじきだしたところで
次のステップです。
ステップ③
ステップ③:出力したデータと教師データ（訓練データ[出力]）を比較し、損失関数を計算する。
あなたが設計したニューラルネットワークはぶち込まれた訓練データ[入力]を基に計算し、
結果を出力しました。
この結果はどうなんでしょうか。
イイのでしょうか？
それともわるいのでしょうか？
それがわからないとニューラルネットワークは学習をすすめることができません。
答え合わせなしで問題を解き続けさせられているようなものです。
これでは勉強ができるようになりませんよね？
そこでイイかわるいかの指標として損失関数を考えます。
損失関数は、出力したデータと教師データ（訓練データ[出力]）から計算される指標です。
あえて乱暴に分かりやすく言ってしまえば損失関数とは出力と正解との誤差のことです。
損失関数として計算される誤差としては、一般的に２乗和誤差や交差エントロピー誤差が使われます。
２乗和誤差は以下の式で計算されます。
E = \frac{1}{2}\sum_{k} (y_k - t_k)^2
E : 損失関数
k : データ数
y : ニューラルネットワークの出力
t : 正解
式についてはこんなもんなんだなーくらいでいいです。原理は重要ではありません。
交差エントロピー誤差は以下の式です。
E = -\sum_{k}t_k\log y_k
E : 損失関数
k : データ数
y : ニューラルネットワークの出力
t : 正解(one-hot表現)
one-hot表現とは正解だけ1で他は0となる表現です。重要ではありません。
logの底はeの自然対数ですが別に重要ではありません（モノを作るためには）
出力結果がイイかわるいかを示す損失関数が計算できたところで次のステップです。
ステップ④
ステップ④:損失関数を基に逆伝播を行い、勾配を計算する。
さて、損失関数が計算できたところで次は何をすればいいのでしょうか？
我々の目的は訓練データの入力と出力の関係をうまく説明できる重みをもつニューラルネットワークを構築することでしたね。
損失関数は誤差でしたから、これが小さい方がより優秀なニューラルネットワークということになります。
つまり次にやることは損失関数を小さくすることです。
どうすれば小さくなるのでしょうか。
とは言っても、我々にできることはニューラルネットワークの重みを更新することだけです。
損失関数が小さく小さくなるように（ゼロになるのが理想）ニューラルネットワークの重みを更新すればいいのです。
では重みをどのように更新していけばいいのでしょうか。
損失関数を一番大きく減らすように重みを更新すればいいのです。
それを繰り返すことがすなわち学習です。
では損失関数を一番大きく減らすにはどうすればいいのでしょうか。
勾配を使えばいいのです。
勾配とは、損失関数の値を最も減らす方向を示すものです。
勾配は数値微分を用いて計算することができます。
微分とは関数上のある点における傾きを求めるアレでしたね。
数値微分は微分ほど厳密ではないが実装が簡単であるという理由で
機械学習でも勾配を求めるのに使われています。
具体的には、対象となる関数の上の非常に近い二点を結び，
その直線の傾きを微分の近似値とします。
ただし、数値微分は数値解析的なアプローチであるため、プログラムにやらせるには
かなり重い時間のかかる処理となります。
そこで逆伝播という手法を用いることで、軽い時間のかからない算出が行えるのです。
逆伝播の詳しい説明は割愛しますが、数値微分の代わりに軽い処理で勾配を算出してくれるんだなくらいの理解でいいと思います。
現在の損失関数に対しての勾配が計算できたところで次のステップです。
逆伝播は軽い処理ですが実装が複雑になることが多いため、ミスも多くなります。
一方数値微分は重い処理ですが実装は簡単です。つまり逆伝播で算出した
勾配が正しい結果になっているかの答え合わせに数値微分が使えます。
逆伝播と数値微分でそれぞれ算出した勾配がほぼ似たような値であれば
逆伝播がうまいこと実装できてそうだなと判断がつきます。
これを勾配確認といいます。
ステップ⑤
ステップ⑤:勾配方向に重みを少しだけ更新する。
現在の損失関数に対しての勾配が計算できました。
その勾配に従ってニューラルネットワークの重みを少しだけ更新すれば、
精度が向上することでしょう。
しかしこの少しだけというのがクセモノです。
めっちゃくちゃ少しだけだったらニューラルネットワークが学習を終えるのに１００年くらいかかるかもしれません。
一方、大きく更新してしまった場合、損失関数をうまく減らすことができません。
以下のように、ちょうどいいところを通り過ぎて更新されてしまうからです。
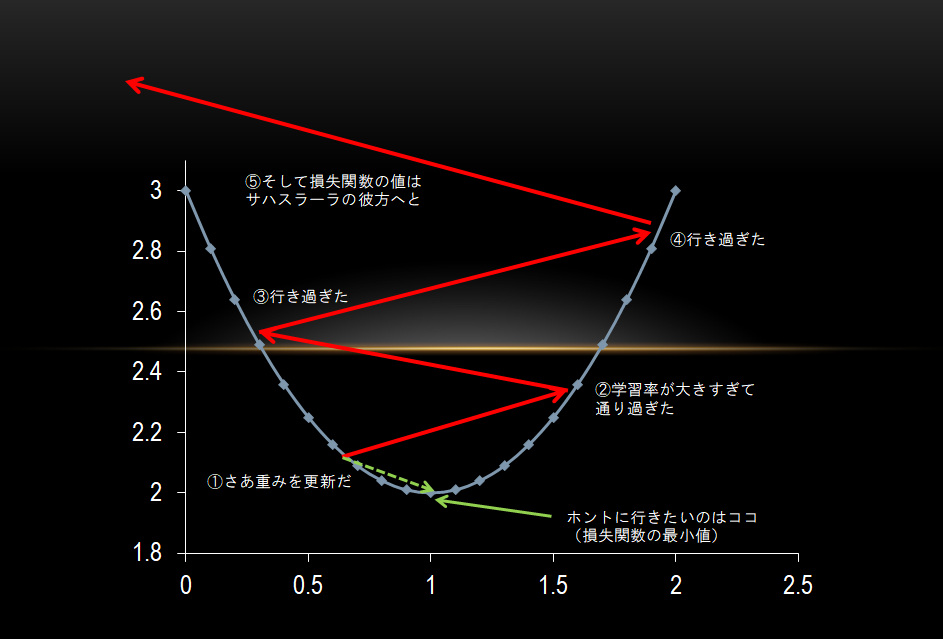
fig.3 大きすぎる重みの更新が損失関数に与える結果
この更新の度合いのことを、学習率といい、これは人間が決めねばなりません。
上述の通り、学習率は一般に、大きすぎても小さすぎても学習はうまくいきません。
学習率の決め方も重みの初期値の決め方と同様、かなり大きなテーマですが割愛します。
妥当な学習率で重みを更新し、学習が進みました。
学習率のように、機械学習において人間が決めなければならないものをハイパーパラメータといいます。
ハイパーパラメータをいろいろ変えて学習させ、最も精度のよいニューラルネットワークのモデルを探すのです。
ステップ①～⑤を繰り返す
以上見てきたステップ①～⑤を繰り返すことでこのニューラルネットワークは学習を重ねます。
そしていい感じの重みをもったニューラルネットワークになれば学習完了です。
いい感じとは何かはご自分で判断してください。
ふつうは推測精度がある値を超えたらオッケーとします。
精度が 70 % 超えるレベルでも使えるのか、 98 % 以上ないといけないものなのかは要件次第です。
競馬を例に言うと、最終的な的中率をどのくらいにしたいのか次第です。
あなたが望む精度を超えたとき、このニューラルネットワークはデータを与えれば勝ち馬を予想するＡＩに成長を遂げたのです。
あとはあなたが発明したそれを使ってバシっと稼ぐだけですね。
学びに必要なのはモチベーションコントロールのみです。自己コントロール。まさにヨガ
まとめ
今回はニューラルネットワークの詳細を説明しました。
機械学習が何をやっているかスッキリと見えてきたのではないでしょうか。
次回はいよいよ簡単なニューラルネットワークを実装していきます。
次回を終えた時、みなさんはオリジナルのニューラルネットワークを作れるようになっているはずです。
簡単なものではありますが。。。でも、とてもとても大きな一歩です。
せーの！サハスラーラ