連続時間のシステムを離散時間に変換する際の近似手法に、双一次変換というものがあります。デジタルフィルタを作る時などに使われたりします。
よく使用される基本的な状態空間表現を使って、双一次変換による離散化の方法を紹介します。
※この記事では双一次変換の特別な場合についてお話ししています。詳細や一般的な変形を知りたい方は、こちらなどを参考にしてください。
変換方法
基本的な連続時間線形時不変システムを、双一次変換を使用して離散時間状態空間に変換します。
変形前がこちら。
\left\{ \begin{eqnarray}
\dot{x} & = & Ax + Bu \\
y & = & Cx
\end{eqnarray} \right.
$x$は状態変数、$y$は出力、$u$は入力です。また、$A$、$B$、$C$は時刻に依存しない係数行列です。
これを、次の形式に変換したいとします。
\left\{ \begin{eqnarray}
\hat{x}[k+1] & = & A_d \hat{x}[k] + B_d u[k] \\
y[k] & = & C_d \hat{x}[k] + D_d u[k]
\end{eqnarray} \right.
$\hat{x}[k]$は離散時刻$k$の状態変数です。係数行列の添え字$d$は離散時間のものであることを表します。
この時の、離散時間の間隔をTとした場合の変換方法はこちらです。
\begin{eqnarray}
A_d & = & \left( I + \frac{T}{2}A \right) \left( I - \frac{T}{2}A \right)^{-1} \\
B_d & = & T \left( I - \frac{T}{2}A \right)^{-1} B \\
C_d & = & C \left( I - \frac{T}{2}A \right)^{-1} \\
D_d & = & \frac{T}{2} C \left( I - \frac{T}{2}A \right)^{-1} B
\end{eqnarray}
変換方法については以上です。
変換例
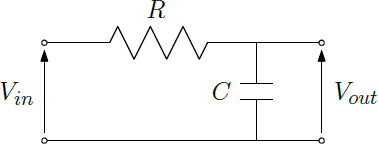
簡単な回路を使ってデジタルローパスフィルタを設計します。$V_{in}$が入力電圧、$V_{out}$が出力電圧です。抵抗$R$とコンデンサ$C$で構成された部分がローパスフィルタとなり、$V_{in}$の高周波成分(ノイズなど)が減衰され、$V_{out}$に出力されます。
回路を流れる電荷を$q$とすると、回路方程式は次のようになります。
\left\{ \begin{eqnarray}
V_{in} & = & R\dot{q} + \frac{1}{C}q \\
V_{out} & = & \frac{1}{C}q
\end{eqnarray} \right.
状態変数を$q$、入力を$V_{in}$、出力を$V_{out}$としたシステムに変形すると、
\left\{ \begin{eqnarray}
\dot{q} & = & -\frac{1}{RC}q + \frac{1}{R}V_{in} \\
V_{out} & = & \frac{1}{C}q
\end{eqnarray} \right.
これは微分方程式で表現されているので、連続時間の状態方程式になります。シミュレーションは離散時間で行うので、双一次変換を使って離散時間状態方程式に変形します。
先にまとめた変換表を参考にシステムの係数を計算すると、次のようになります。離散時間の間隔は$T$とします。
\left\{ \begin{eqnarray}
\hat{q}[k+1] & = & \frac{2RC-T}{2RC+T}\hat{q}[k] + \frac{2CT}{2RC+T}V_{in}[k] \\
V_{out}[k] & = & \frac{2R}{2RC+T}\hat{q}[k] + \frac{T}{2RC+T}V_{in}[k]
\end{eqnarray} \right.
これで離散化は完了です。あとは$V_{in}$に適当な信号データを入力し、$V_{out}$を取得すればデジタルローパスフィルタの完成です。
(おまけ)シミュレーション
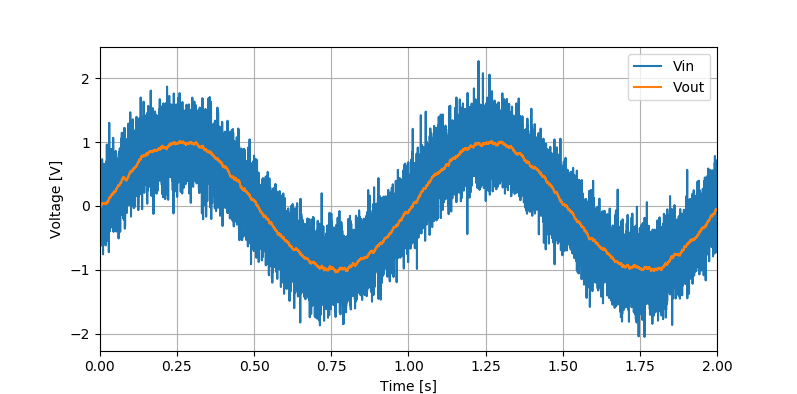
上で求めたデジタルローパスフィルタを使ってノイズ除去をやってみました。入力は$$V_{in}=\sin(2\pi t) + 0.3\varepsilon$$ としています。$\varepsilon$は平均0、標準偏差1のガウスノイズです。ノイズが除去されているのがわかりますね。
以上です。ありがとうございました。