ちょっと風邪引いてたり研究に集中してたりして遅くなりました。
アドベントカレンダーを勝手に改称して2016年カウントダウンカレンダーにしたいと思います。
来年の1/27に出すIJCAI論文のネタが結構いい感じに進んでいるので、今後のカレンダーは、自分の研究の方が実験結果待ちの間に書く感じで進めていきたいと考えています。毎日はやっぱ優先度的にも面白み的にも無理っすね・・・
GBFS のおさらい
一週間も休んでいたので、もうGBFSを忘れてしまった方も多いかもしれません。GBFSは、 A* の $g$ 値を無視して、見積もり値 $h$ だけを使ってガンガン探索を進めるタイプのアルゴリズムでした。最適性は気にせず兎に角素早く解を見つけたい場合には、GBFSは簡単で便利な手法です。
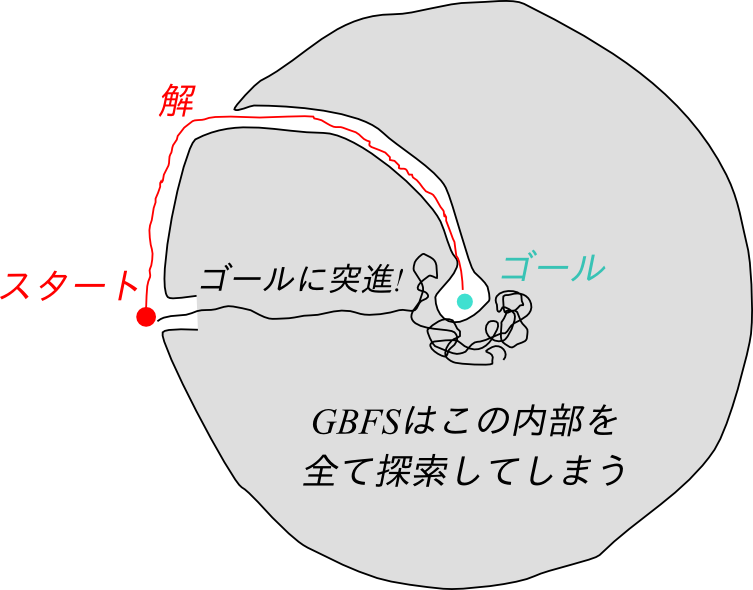
しかし、GBFSにも、解の全く存在しない領域をウロウロしてしまうことがあります。これが、前回触れた二つ目の課題、「不正確な$h$の見積に騙されてトラップにハマってしまう」 という点でした。
GBFSをだますようなトラップの例を下の図に示しました。ヒューリスティクス$h$には、ユークリッド距離を使うと仮定します。GBFSは、OPENリスト中で最小の$h$を持つノードを常に展開するので、まるで電灯に集まる虫けらのように探索してしまいます。トラップの内部を全て探索し終えるまで、スタート地点からの別の選択肢を振り返って考えるという動作が出来ないのです。
KBFS (Felner, Kraus, Korf JAIR 03)
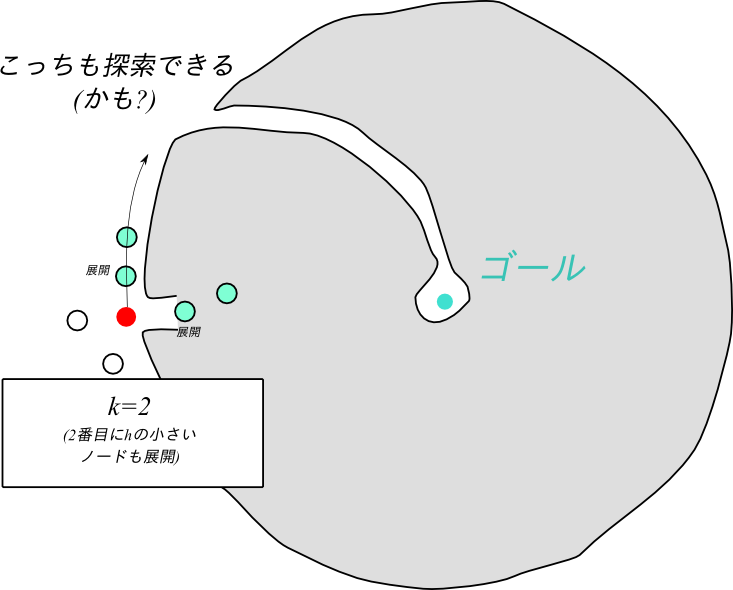
この問題点を改善するための単純な提案の1つが、K-Best-First-Search, KBFS です。これは、ある与えられた定数$k$に対して、オープンリストから同時に$k$個一気に取り出しそれを全て展開するというアルゴリズムです。スタート時点から既に最良 だけではなく k番目の最良 も展開するので、状況によっては展開数が増えますが、上の例を改善することが出来ます。
KBFSにおいて、 $k=1$ のケースはGBFSに一致します。また、$k=\infty$ の場合は幅優先探索に一致します。なぜなら、新たに生成されたノードが、OPENに入っているノードを展開し終えた後にしか展開されないからです。
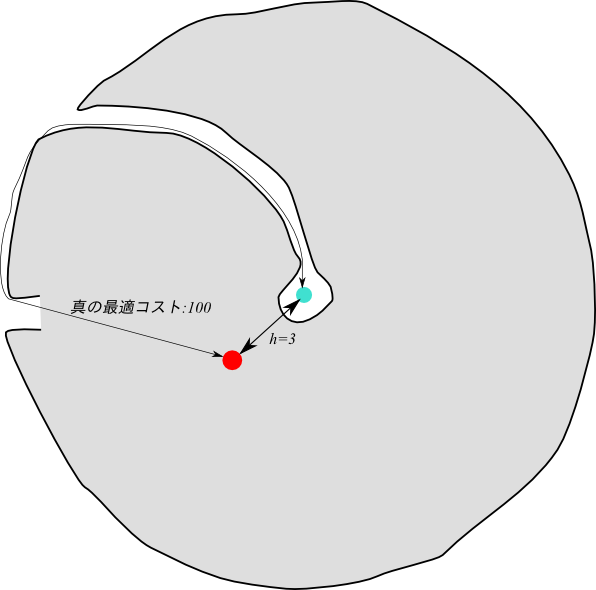
(Felner, Kraus, Korf JAIR 03) は、$h$ のエラーが大きいノードの数が増えるほど、 大きな$k$ を用いるKBFSがより良い性能を持つということを実験的に示しました。今の例でいうとユークリッド距離は、下の図に示すように、壁の存在を考慮していないが故にとても大きなエラーを含むヒューリスティクスです。
KBFSにはEKBFSとかいう発展もあるらしいです。(Linares, Lopez, Borrajo 2010)
Diverse BFS (Imai, Kishimoto, AAAI 2011)
たぶん、KBFSはそれ自体有用なアルゴリズムではありません。第一、問題の$h$がどの程度エラーを含んでいるのかどうかは、問題を解き終わってみなければわかりません。従って、適切な$k$というのはぶっちゃけよくわかりません。
DBFS (Diverse Best First Search) は、これをより発展させたアルゴリズムです。
DBFSは、基本はヒューリスティクスに従うGBFSを行いつつも、$h$にエラーがあっても大丈夫なように、スタートに近い様々なノードも乱択に基づいて展開します。このようにすることで、展開されるノードにDiversity(多様性)を設け、$h$のエラーが大きいような領域ばかりに探索が集中しないようにするのです。これは、SATにおける木探索で用いられているリスタート手法とある程度類似しています。
DBFSは、各ループごとに、あるノード$n$ をOPENからある程度ランダムに選び出し、その$n$を開始点として最大の展開ノード数を$h(n)$ に制限されたGBFSを行います。そのため、グローバルなOPENと、ループ内のGBFSが持つLocal OPENが別に存在します。Local OPENは、GBFSが中止された時点でOPENにマージされます。
Algorithm DBFS
- insert the root node into OPEN
- while OPEN is not empty do
- $n \leftarrow fetch(OPEN)$
- $Local OPEN \leftarrow {n}$
- $i\leftarrow 0$
- while $i < h(n)$ do
- $GBFS(n,LocalOPEN)$
- $i++$
- $OPEN \leftarrow Local OPEN \cup OPEN$
- return no solution
次に、「ある程度ランダムに選び出す」サブルーチンである、3行目の $fetch$ を解説します。
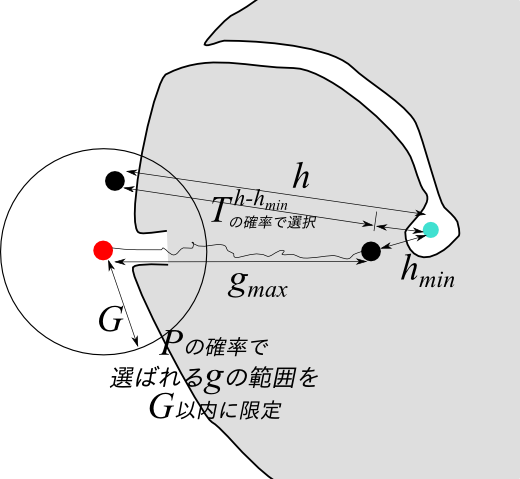
まず、 $h_{min},h_{max},g_{min},g_{max}$という値が登場します。これらは、グローバルOPENに含まれている$g,h$の最大・最小値です。また、アルゴリズム全体のメタパラメータとして$P,T$を用います。どちらも範囲 $[0,1]$ の実数です。かつ、OPENは $(g,h)$ ごとに独立なQueueで構成されており、 $pop(OPEN, (g,h))$ や $isEmpty(OPEN, (g,h))$ という操作が出来るものとします。
Subroutine $fetch$
- 確率 $P$ で成功する Coin Flip
- 成功すれば $G \leftarrow 範囲 [g_{min}, g_{max}]$ からランダムに選択
- 失敗すれば $G \leftarrow g_{max}$
- for all $(g,h)$ in $[g_{min},g_{max}]\times[h_{min},h_{max}]$ do
- $p[h][g] \leftarrow $
- if $(g>G) \lor isEmpty(OPEN,(g,h))$
- then 0
- else $T^{h-h_{min}}$
- if $(g>G) \lor isEmpty(OPEN,(g,h))$
- $p[h][g] \leftarrow $
- $p_{total} \leftarrow \sum_{g,h} p[h][g]$
- $(g,h)$ を確率 $p[h][g]/p_{total}$ で乱択
- return $pop(OPEN,(g,h))$
ここで、確率$P$ のCoin Flip が成功すれば、探索は今までの探索領域をさかのぼってより根本に近いノードを選択します。失敗すれば、最も$g$の大きいノードが選択されることになります。GBFSは$h$ の最も小さいノードを展開しますが、この動作によりどんどん長い経路を探索するので、展開されるノードの$g$ も大きい傾向があります。従って、失敗のケースはGBFSと似た動作に近づきます。
$P$ は $g$ に基づく確率を操作しますが、一方 $T$は、$h$ に基づく確率を操作します。$T$を一言で言い表わせば、「ヒューリスティクスをどれだけ信頼しないか」です。$T$の肩に乗っかっているのは、「ヒューリスティクスによれば現在一番良いとされている」値$h_{min}$ と、 $h$ との差です。$T$が大きければ、 $h_{min}$ から離れた $h$ を持つノードが選ばれやすくなります。
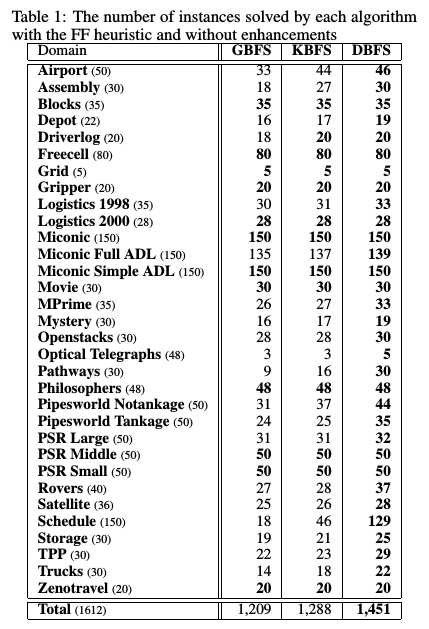
今井さんによれば、International Planning Competition 問題集に対し、DBFSは同じ時間・同じメモリ制限で、 GBFS, $\max_{l\in [0..7]} KBFS({2^l}) $ と比べ 200題以上大きな問題を解くことができています。改善は特定ドメインに偏っているわけではなく、様々なグラフ探索問題全般で効いていることがわかります。
まとめ
DBFSすっごい! でした。
正直、今までの内容は教科書にも載っている内容でしたが、ここからは教科書にも載っていない最新の内容に移っていくつもりです。