はじめに
趣味で作ったスプラ神経衰弱で使われているグラフ理論の知識を紹介し、グラフ理論のアルゴリズムがどのように実問題に応用されているかを楽しく学ぼう、という趣旨の記事です。
アプリを公開してあるので、よかったら遊んでみてください。
(追記)
公開していたアプリは閉じたので、アクセスできなくなりました。
(追記終わり)
アプリの概要説明
自分のブログの方に、ルールや開発時に困ったことや実装の中身の一部などを書いたので、詳しくはそちらを読んでいただきたいです。
ここでは、この記事を読むために必要な部分に絞って簡単に概要を説明します。
基本的には通常の神経衰弱と同じルールです。
通常の神経衰弱と異なる点は、ペアになるカードの相手が多岐にわたること、ペアの珍しさによって得点が変わることです。
スプラ神経衰弱では、スプラトゥーンのブキが書かれた各カードをめくって、ペアにしていきます。
スプラトゥーンには多くのブキが存在し、各ブキはメインウェポン、サブウェポン、スペシャルウェポンが設定されています。
上図だと、左にメインウェポンが、サブウェポンとスペシャルウェポンが右側に表示されています。
スプラ神経衰弱では、ブキのメインウェポン、サブウェポン、スペシャルウェポンのうちいずれかが一致していたらペアにすることができます。
また、ペアになったときの得点もペアの種類によって変わるようにします。
珍しいペアを手に入れたときは高得点が入り、ペアにしやすいようなカードの組であれば低い得点になるようにします。
この得点の設定ロジックについては本記事では割愛します。
ブキをノード、ペアになりうるかをエッジ、ペアになったときの得点をエッジの重みとすることで、重みつきの無向グラフと見ることができます。
今回はこの重みつきの無向グラフを題材に、スプラ神経衰弱で必要とされるグラフ理論の知識を学んでいきたいと思います。
どのカードをゲームに使う?~連結な部分グラフ~
今回はスプラトゥーン2のブキを対象にしたので、全部で139種類のカードがあります。
これらをすべて使って神経衰弱をすると本当に神経が衰弱するので、一部分だけを取り出してきてゲームに使用したいです。(今回は12種類をゲームに使います。)
一番簡単なのは、139種類のブキから完全にランダムに重複を許さずに選んでくる方法ですが、この方法だと作れるペアの数が少なくなってしまうことが起こりやすくなってしまいます。
このように、
- 毎回カードの種類は変わってほしい
- かつ、ある程度ペアは作りやすい
というカードの集合をとってきたいという要件です。
今回はこの要件を満たすために、
- 一つランダムにブキを選んでもってくる
- 現在選んでいるブキのいずれかとペアになりうるようなブキの候補からランダムに取得
- 12個集まるまで2を続ける
というアルゴリズムにしました。
ブキをノード、ペアになるかをエッジとしてグラフを作ったときに、始点ノードをランダムに選んでそのノードを含む一つの連結な部分グラフをサンプルする、ということですね。
Pythonで実装したものがこちらです。
def get_connected_subgraph(mat, seed_node, nodes_num):
"""隣接行列と、seedとなるノードを受け取り、ノード数がnodes_numの連結部分グラフを返す."""
ans = {seed_node}
while len(ans) < nodes_num:
sampled = random.sample(ans, 1)[0]
connected_nodes = set(np.where(mat[sampled] > 0)[0].tolist())
candidates = list(connected_nodes - ans)
if len(candidates) == 0:
raise Exception("Failed.")
to_be_added = random.choice(candidates)
ans.add(to_be_added)
return list(ans)
もちろん連結成分が一つでなくてもいいのですが、要素数が小さい連結成分がある部分グラフをとってきてしまうと、ペアの多様性が小さくなってしまいゲームが面白くないので、連結成分は一つにしました。
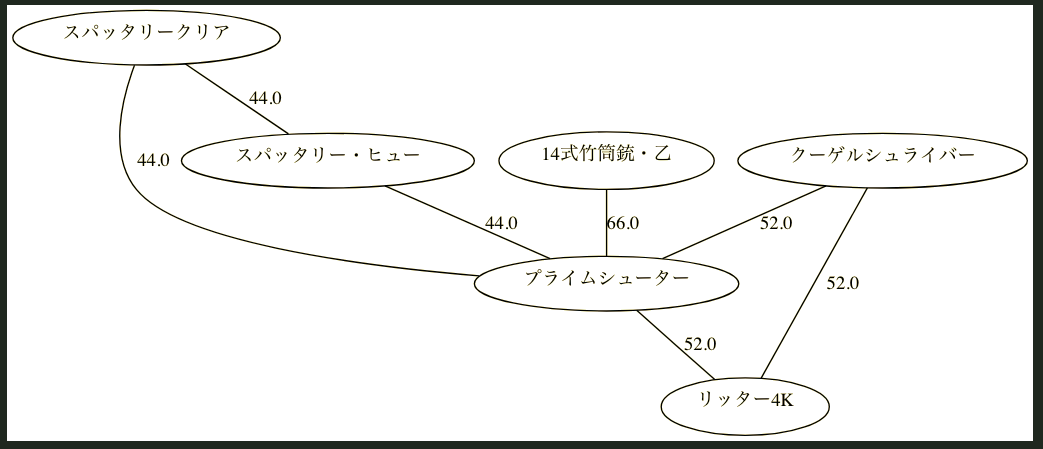
このコードでランダムに取得してきたグラフを描画したものがこちらになります。
12個だと多くてわかりづらいので6個に絞っています。
全てのカードが取りきれる? ~完全マッチング~
完全マッチング
前章のアルゴリズムで取得した連結な部分グラフは、ある程度ペアは作りやすくなっています。
連結なので、ゲーム開始時点ではどのカードもペアになりうる相手が存在しています。
ですが、連結だからと言って必ずしも全てのカードを取り切ることができるとは限りません。
以下がその例です。どうしても2つのノードが余ってしまいます。
グラフの中にあるノードから、エッジで繋がれているノードどうしでペアを作る問題をマッチングといいます。
(同じノードは二度使えません。)
今回考えたいのは、「得られたグラフのノードをマッチングしていったときに、すべてのノードを使い切るようなマッチングができるか?」という問題です。
このように、すべてのノードを余さずに使うようなマッチングを完全マッチングといいます。
今回の場合、とってきたカードの集合(でできているグラフ)が完全マッチングが存在するようなグラフであれば、うまく行けば全てのカードをとりきることができるというカードの集合である、と言えます。
あるグラフの部分グラフのうち完全マッチングが存在するグラフを直接とってくるのが難しそう(いい方法があったら教えて下さい)なので、
今回は先ほど説明した部分グラフの取り方を使って手に入れたグラフが、「完全マッチングが存在するグラフであるか?」を判定することにします。
完全マッチングが存在するグラフがでるまでサンプルし続ける、というロジックにしました。
完全マッチングの判定
「完全マッチングが存在するグラフであるか?」の判定ですが、こちらはTutteの定理を使って判定することができます。
参考 : Tutteの定理と友達になりたい
この定理の通りに判定ロジックを実装しました。
Pythonで書いてあります。
from scipy.sparse import csr_matrix
from scipy.sparse.csgraph import connected_components
import itertools
def get_all_sub_indexes(repeat_num):
"""bit全探索用"""
sub_indexes = []
for case in itertools.product([0, 1], repeat=repeat_num):
sub_indexes.append([i for i, v in enumerate(case) if v == 1])
return sub_indexes
def exists_perfect_matching(G):
"""グラフの隣接行列を受け取って、完全グラフを含むかを判定する."""
size_G = G.shape[0]
sub_indexes = get_all_sub_indexes(size_G)
for sub_index in sub_indexes:
# sub_indexはG-Uに相当
size_U = size_G-len(sub_index)
G_minus_U = G[np.ix_(sub_index, sub_index)]
# 連結成分に分解
csr_graph = csr_matrix(G_minus_U)
_, groups = connected_components(csr_graph, directed=False)
conntected_nodes = collections.Counter(groups)
odd_G_minus_U = len(
[freq for freq in conntected_nodes.values() if freq % 2 == 1])
if odd_G_minus_U > size_U: # Tutteの定理より
return False
return True
ノード集合に対してbit全探索して、元のグラフからノードを取り除いて連結成分に分解し、ノード数が奇数の連結成分の個数を数えてTutteの定理の不等式で判定します。
bit全探索はitertoolsを、連結成分分解はscipyを使っています。
ノード数が12であれば少し時間がかかるなーぐらいでした。
bit全探索の部分で$O(2^n)$かかるので、もう少しノード数が大きいと重くなりそうです。
完全マッチングが存在するグラフがでるまでサンプルし続ける、というロジックにしたわけですが、
完全マッチングが出にくいと、アクセスしたときにレイテンシが大きくなってしまうか心配だったので、実験しました。
ノード数12で、ランダムに(しかし連結ではある)グラフをとってきて、それが完全マッチングを含むかを調べてみると、100回シミュレーションして完全マッチングを含まないグラフだったのは1回だけでした。
1%くらいの確率で2回完全マッチングの判定が走ってしまうので、少し重いなーと感じた方はその1%かもしれません。
もとのグラフがかなり密なグラフなので、完全マッチングになりやすいのかもしれないです。
(連結なグラフを持ってくることで、完全マッチングになりやすい候補を持ってきているのが効いているのももちろんあると思いますが)
「絶対に全てのカードをとれるグラフ」は作れない?
先ほど、完全マッチングが存在するグラフ=うまく行けば全てのカードをとりきることができるグラフという奥歯に物が挟まった言い方をしましたが、完全マッチングが存在するグラフだからといって絶対に全てのカードが取りきれるわけではありません。
完全マッチングが存在しても、完全マッチングでないマッチングになってしまうことがあります。
ここでまたグラフ理論の用語ですが、「これ以上ペアを追加できないようなマッチング」を極大マッチングといいます。
今回のスプラ神経衰弱でいうと、これ以上ペアが増やせない状態のマッチングのことです。
ゲームの終了条件は、カードをペアにしていき、マッチングが極大マッチングになったとき、ということができます。
完全マッチングが存在するからといって、極大マッチングがすべて完全マッチングとは言えないので、先ほどのうまく行けば全てのカードをとりきることができるという言い回しになってしまったということです。
従来の神経衰弱は、全ての極大マッチングが完全マッチングなので、どんな取り方をしても最終的にすべてのカードを取り切ることが可能というわけです。
では、与えられたグラフについて、「全ての極大マッチングが完全マッチングか?」を判定することができればいいのでは?と思いますが、こちらは難しそうでした。
最小極大マッチングが完全マッチングかを判定するわけですが、最小極大マッチングを見つけること自体が厳しいようなので、諦めました。
このため、完全マッチングが存在するグラフを用いているだけなので、完全マッチングではないの極大マッチングに陥ってしまう問題は残ったままです。
最後の2枚がペアにならずに終了した時の図。
理論上の最高点は? ~最大重みマッチング~
グラフをサンプリングしてくる部分の他に、もう一つグラフ理論を使った処理があったので紹介します。
先述した通りにサンプリングしてきたカード集合を用いて、神経衰弱をしていくわけですが、サンプリングしたグラフごとに獲得することができる最高得点が変わるため、自分が取った点数が高いのか低いのかがわかりづらいという問題点があります。
そのため、グラフをサンプリングしてきた段階でそのグラフで神経衰弱をした際に、獲得できる最高得点を計算して表示できると嬉しいです。
この問題をグラフ理論的に言うと、最大重みマッチング問題となります。
最大重みマッチング問題は、マッチングのうち、重みの和が最大になるようなマッチングを探す問題であり、今回やりたいことと一致しています。
こちらはPython実装があるようだったので、こちらを使いました。
参考 : 組合せ最適化 - 典型問題 - 重みマッチング問題 - Qiita
import networkx as nx
from ortoolpy import graph_from_table
def get_max_weight_matching(mat):
node_df = pd.DataFrame({"id": list(range(len(mat)))})
edge_df = graph2df(mat)
g = graph_from_table(node_df, edge_df)[0]
d = nx.max_weight_matching(g)
return sum([mat[k, v] for k, v in d.items()])/2 # 二回カウントしてしまうので
def graph2df(graph):
edge_df = pd.DataFrame(columns=['node1', 'node2', 'weight'])
for i in range(graph.shape[0]):
for j in range(i, graph.shape[1]):
if graph[i, j] > 0:
edge_df = edge_df.append(
{'node1': i, 'node2': j, 'weight': graph[i, j]}, ignore_index=True)
return edge_df.astype("int64")
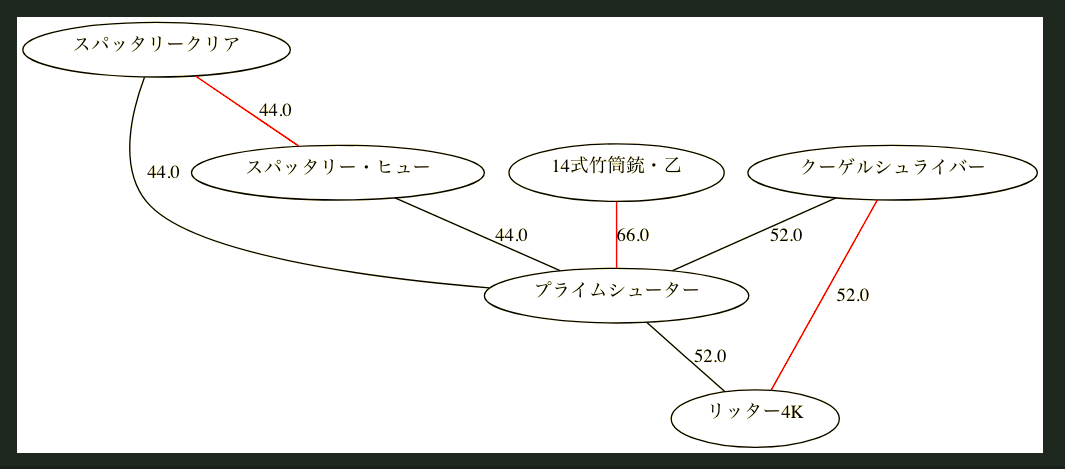
先ほど取得したこのグラフに対して、最大重みマッチングを求めてみます。
これが、
こうマッチングされます。
このグラフでの最高得点の理論値は162、と計算できました。
余談ですが、今回の結果は、最大重みマッチングは完全マッチングになっていますが、一般には必ずしも一致するとは限らないです。
つまり、この図のように全てのカードを取り切ったとしても、最高得点に届かないことはありうる、ということですね。
おわりに
今回は、スプラ神経衰弱という自作アプリを題材に、内部で使用されているグラフ理論、中でも特にマッチングについて学ぶという内容でした。
グラフ理論に限らず、数学が実際の問題に応用されている場面を見るとワクワクします。
実際に問題に直面した際に、「あのアルゴリズムが使えるのでは?」という引き出しをたくさん持っておきたいと思います。
最後までお読みいただきありがとうございました!