単純な規則に従っているだけなのに、結果として複雑な現象が生じることをカオスといいます(※余談1)。宮脇によると、カオスの特性には以下があります。
- 単純な規則から複雑な振る舞いが生じること
- 初期値の敏感性
前者はほぼ定義通りで、後者は「最初の小さなズレが後々とてつもない差になってしまう」ということを意味しています。バタフライ・エフェクトという名前で知っている方もいるのではないでしょうか。(※余談2)
「カオス」や「バタフライ・エフェクト」をもっと感覚的には理解したいなと思っていたところ、前述の論文に出会い、ロジスティックス写像と呼ばれるものの存在を知りました。
今回はPythonを使ってロジスティックス写像を表現し、カオスの2つの性質を確認することにします。
ロジスティックス写像とは
難しそうな名前をしていますが安心してください。名前以外は難しくありません。
今年の人口から来年の人口を表現するとします。$X_{○○}$を〇〇(今年または来年)における人口とすると、来年の人口は以下の式で表されます。
$$X_{来年} = c \cdot{} X_{今年} \cdot{} (1 - X_{今年})$$
中学生で習う二次関数に似ていますね。$X$は0から1までの値をとることに気をつけてください。コミュニティが持ちうる人口に対する現在の人口の割合と理解するのが知れません。
aは係数で、これが大きくなると来年分の変動も大きくなります。僕は合計特殊出生率や基本再生産数と関連して理解しています(※余談3)。
人が増えすぎると食糧や住処などに問題が生じます。人口が増えすぎたときに減らそうとする作用を$(1 - X_{今年})$で表しています。
この式を繰り返し計算することで今年から来年、来年から再来年の人口を表現することができるのです。
論文によると係数$c$が3.5699456...以上のとき、ロジスティックス写像の振る舞いがカオスになり**$X$は絶対に同じ値を取らず、周期を持たなくなるそうです。さらに、この係数では初期値を少しずらしただけで、後の振る舞いは全く違ったものになる**ということです。
繰り返しますが上の式はいたってシンプルです。この式から本当に無秩序な結果が出るのかをPythonで確認しましょう。
Pythonで表現
まず、ロジスティックス写像を超単純に表します。
def logistic_map(x, a):
return a * x * (1 - x)
今回は係数として以下を用意します。
coefs = [1, 2, 3, 3.2, 3.5, 3.6, 3.9, 4, 4.2]
初期値を適当な値に設定して、各係数について100年後までの人口推移をグラフで表します。(りすと)
x = 0.3
for c in coefs:
Xs = []
Xs.append(x)
for _ in range(100):
x_old = x
x = logistic_map(x_old, c)
Xs.append(x)
plt.title(f'c = {c}')
plt.ylim(0, 1)
plt.plot(Xs)
plt.show()
結果 - 第1性質: 単純なルールから複雑な振る舞い
Wikipedia(ロジスティックス写像)に準じて係数$c$を以下の条件で分け、人口の推移を見ることで、単純なロジスティックス写像の式から複雑な振る舞いが生まれることを確認します。
- cが0以上1以下のとき
- cが1より大きく2以下のとき
- cが2より大きく3以下のとき
- cが3より大きく3.44...以下のとき
- cが3.44...より大きく3.56...以下のとき
- cが3.56...より大きく4より小さいとき (カオス発生)
- c = 4 のとき (ピュアカオス)
- cが4より大きいとき (マイナスの無限大へ)
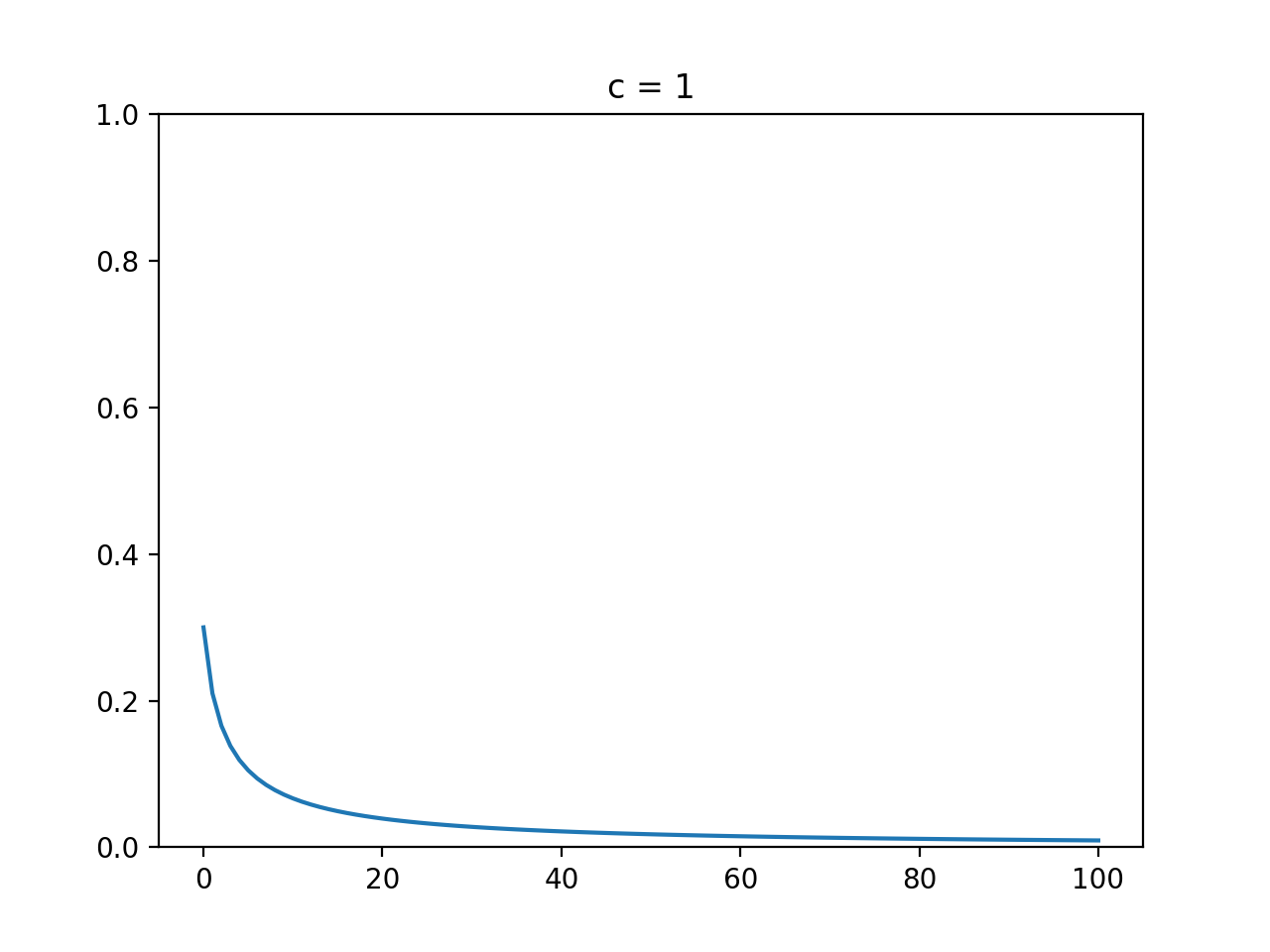
cが0以上1以下のとき
初期値に関わらずゆっくりと減衰していき最終的には0に収束します。これは式からも想像できますね。以下は$c = 1$におけるグラフです。
きれいに減衰していますね。
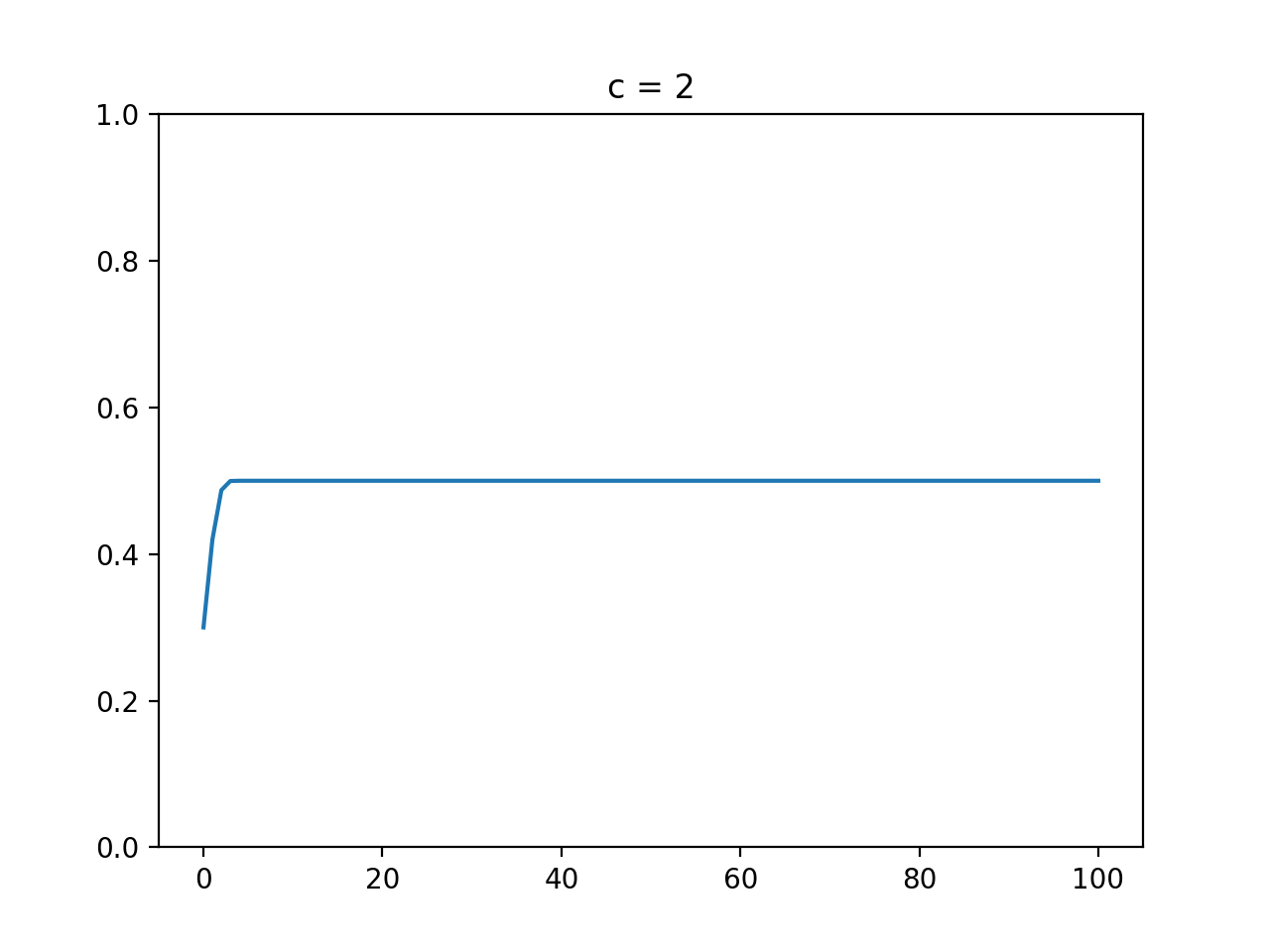
cが1より大きく2以下のとき
単調増加(減少)しながら$1 - \frac 1 c$に収束します。この辺はまだ極限をとれば計算できる気がします。以下は$c = 2$におけるグラフです(境界値ばっかで可視化する人🙋♂️)。
今回は収束値0.5が初期値0.3よりも大きい値だったので単純増加しながら収束しました。
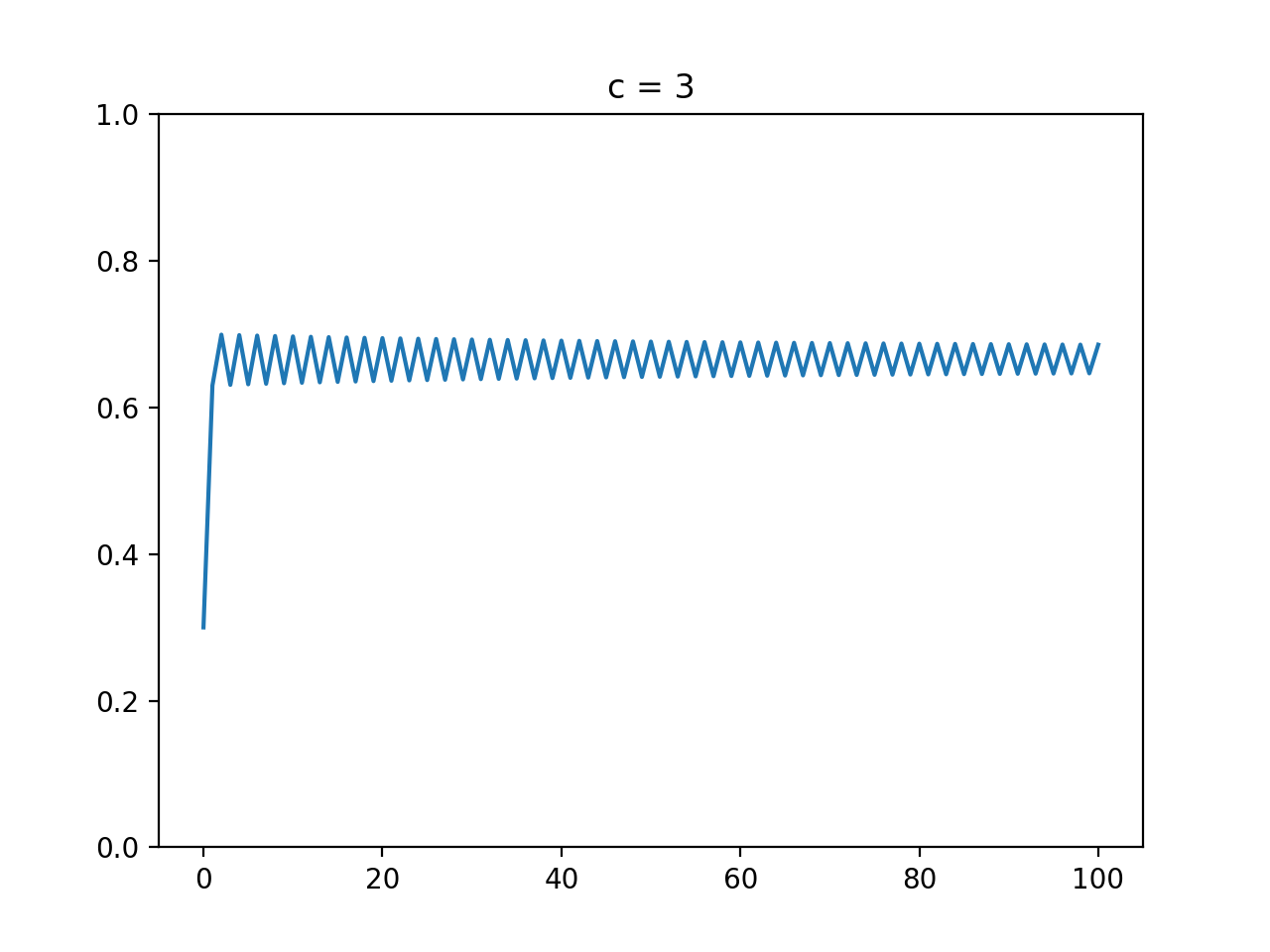
cが2より大きく3以下のとき
$1 - \frac 1 c$付近で振動しながら、最後は$1 - \frac 1 c$に収束します。以下は$c = 3$におけるグラフです(🙋♂️)。
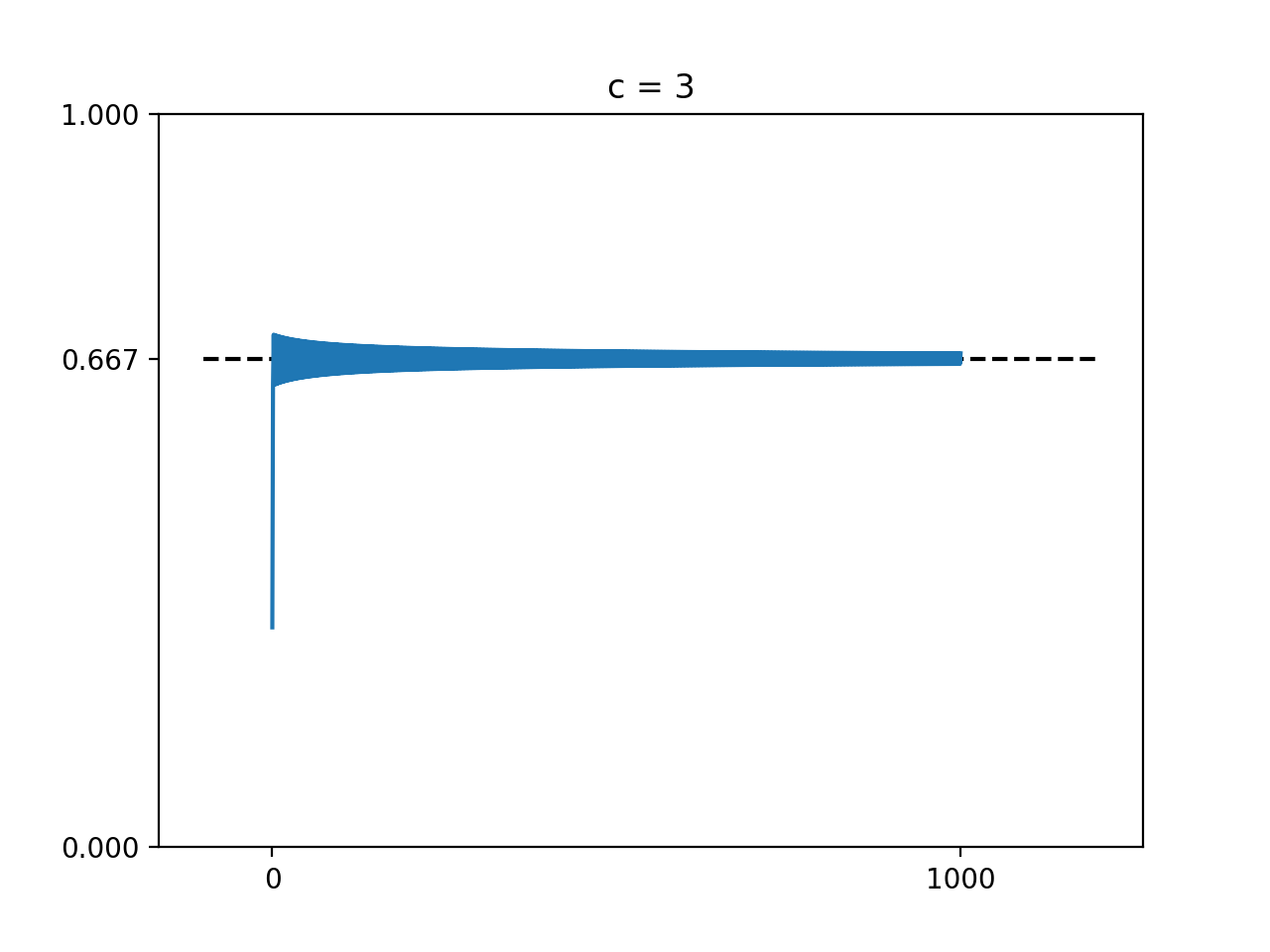
確かに$\frac 2 3 (0.67= 1 - \frac 1 3)$付近で振動しているように見えますね。これだと本当に収束しているか分かりづらいのでもう少し長い期間の推移を見ましょう。
良さそうですね
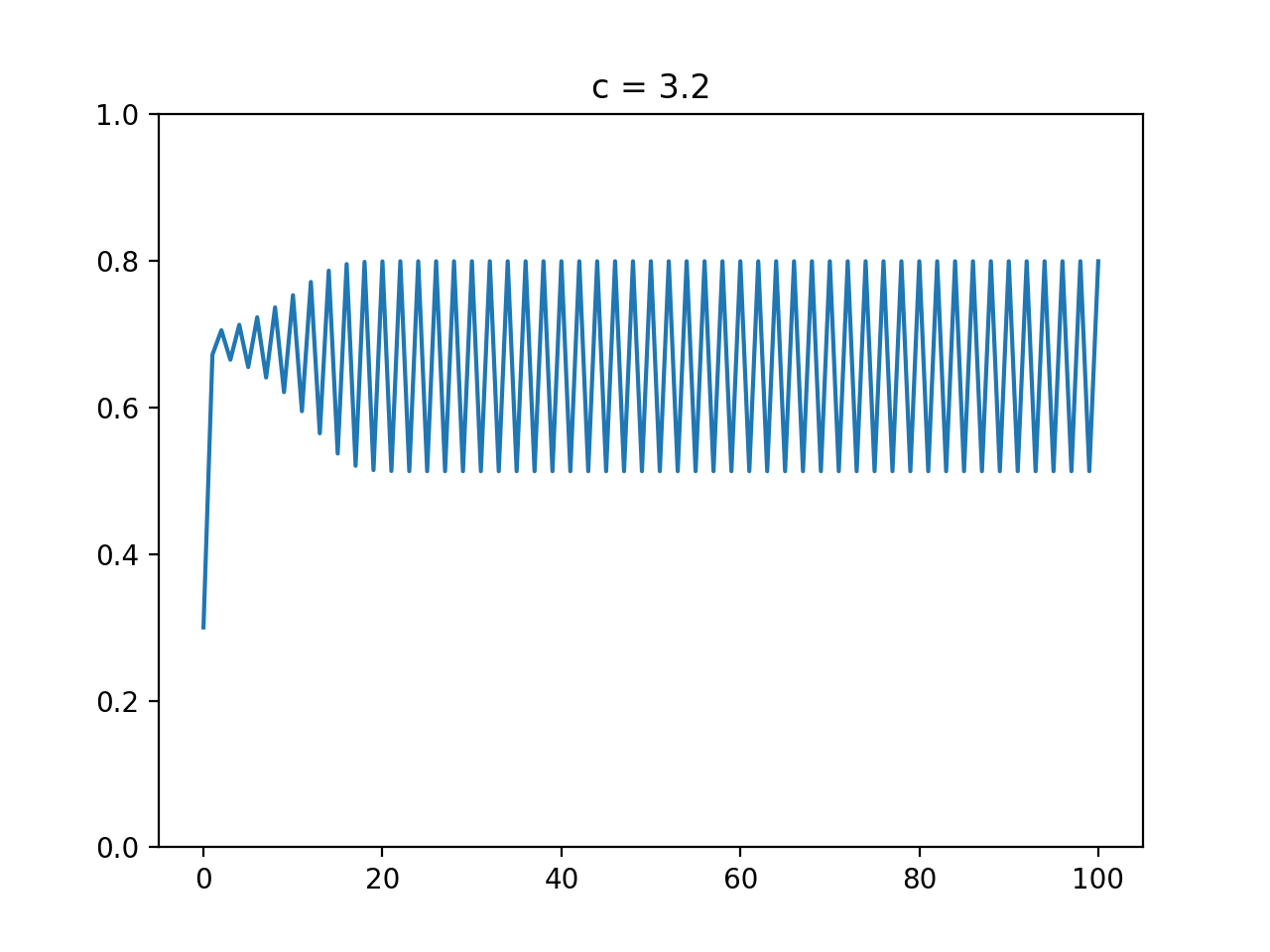
cが3より大きく3.44...以下のとき
収束せず、2つの値の間を行ったり来たりします。この2つの値を周期点と呼ぶみたいです。以下は$c = 3.2$におけるグラフです。
0.5と0.8の間あたりを行ったりきたりしていますね。
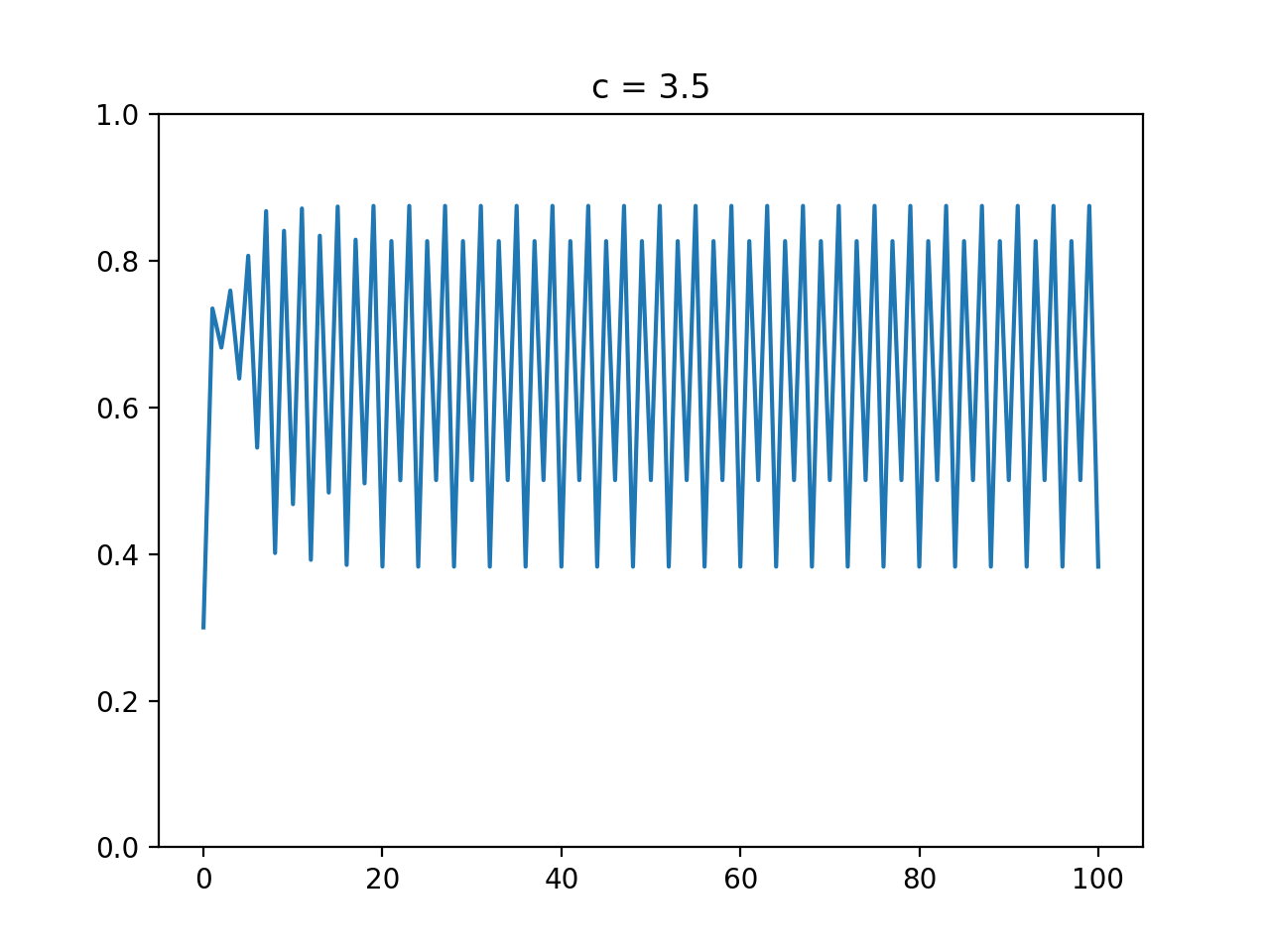
cが3.44...より大きく3.56...以下のとき
2つあった周期点が4つ、8つ…と倍々に増えていきます。実際の周期点の数は$c$の値によるようです。以下は$c = 3.5$におけるグラフです。
周期点が4つあるように見えますね。
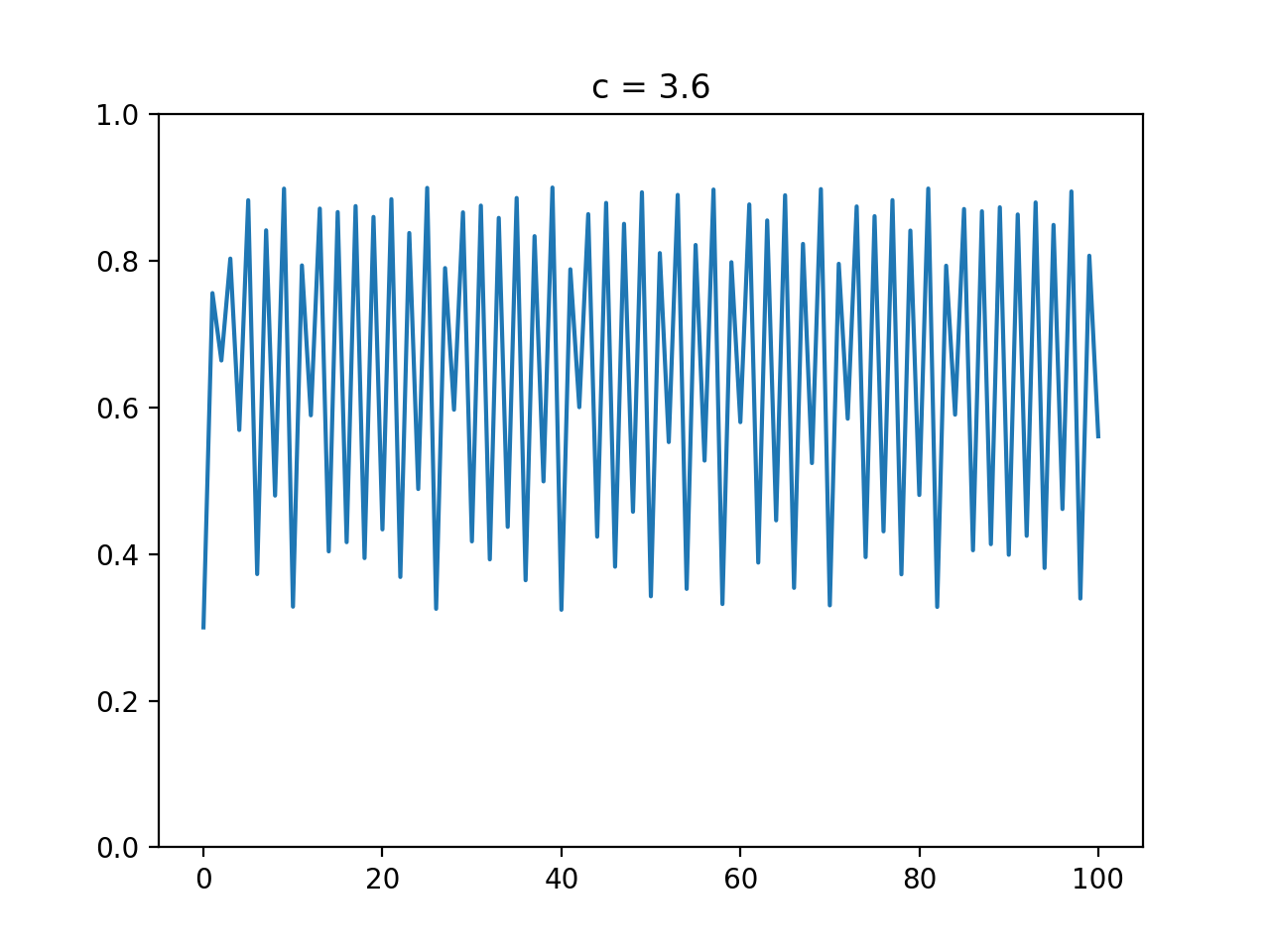
cが3.56...より大きく4より小さいとき (カオス発生)
おめでとうございます、カオス発生です。一貫した収束や周期性がなく、複雑な挙動を示すようになります。以下は$c = 3.6$におけるグラフです。
0.3から0.9くらいの間を不規則に動き回っています。時間によって周期性があったりなかったりします。まさにカオスですね。パット見、$c=3.5$との違いがわかりにくいですが、初期値敏感性を見ると違いがはっきりします(後述)。
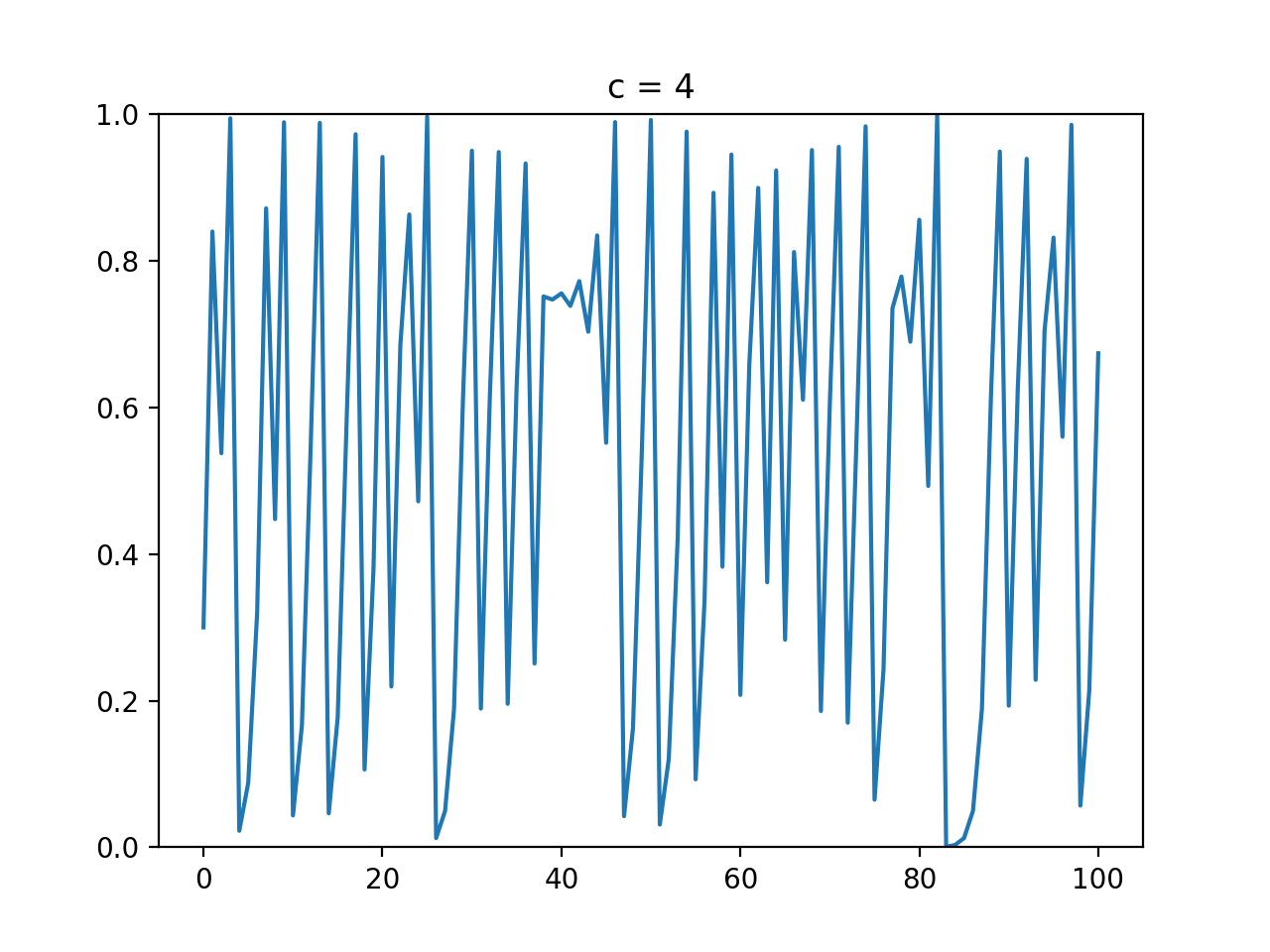
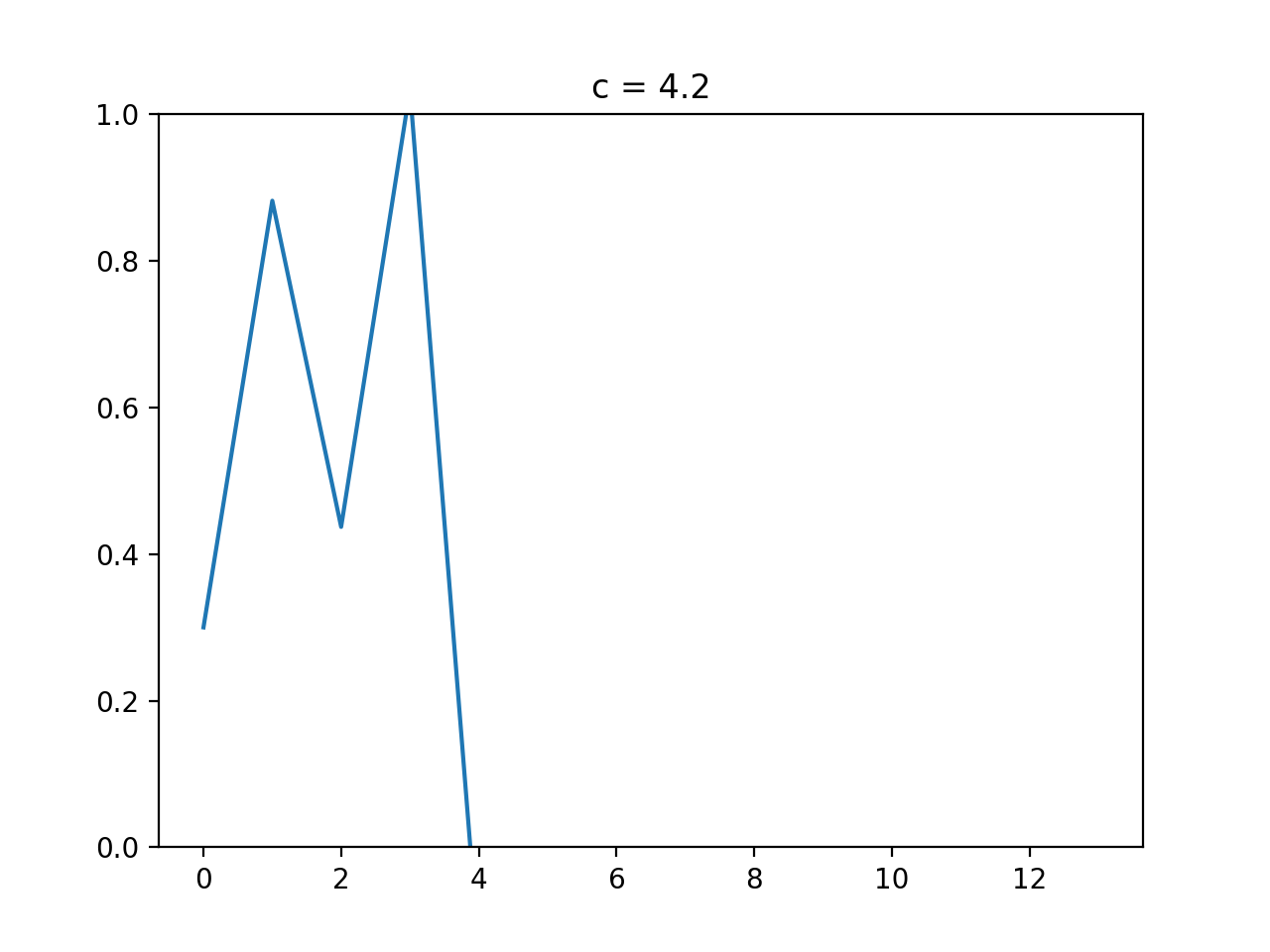
c = 4 のとき (ピュアカオス)
より変化量の大きいカオスです。$X$は0から1、つまり取りうる値をどれでもとることができます。
これをピュアカオスというらしいです。中二病っぽい名前ですが、グラフを見るとたしかにカオスです。あの単純なロジスティックス写像の式からは想像もできないような推移をしています。
cが4より大きいとき
マイナスの無限大へと発散します。人口増加や感染症のアナロジーとして考えると興味深いですね。
人口が極限まで増えた結果、人類は滅亡した (※余談4)
結果 - 第2性質:バタフライ・エフェクトの検証
上のグラフを見ただけだと$c=3.6$が本当にカオスなのか少し分かりづらいですね。ここでは、初期値敏感性(バタフライ・エフェクト)を満たすかどうかでカオスの判別をしていきます。
ここでは初期値として$3±0.1$を用意し、元々の初期値と比較します。カオスであればこの小さな初期値の違いに敏感に反応して、推移が異なるグラフになるはずです。
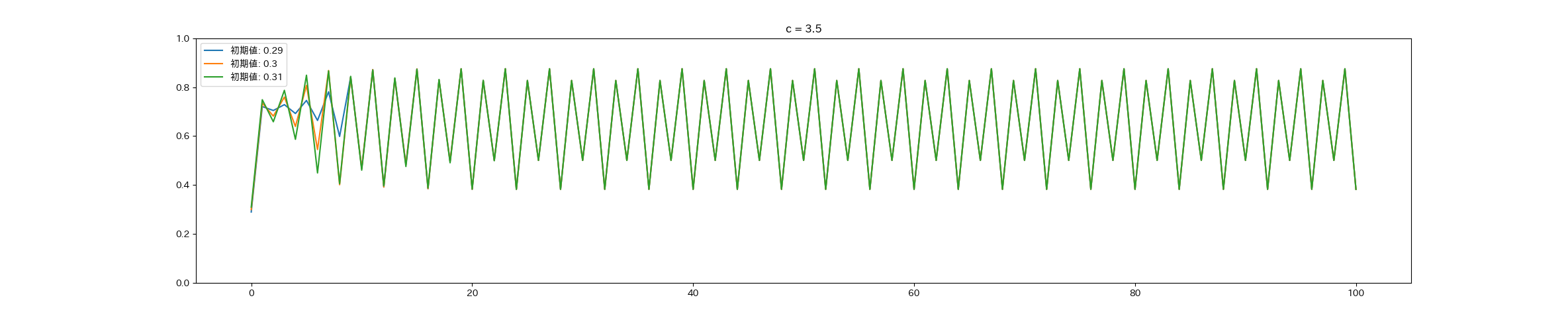
c = 3.5のとき (非カオス)
まずは比較対象として非カオスである$c = 3.5$のグラフを見てみましょう。
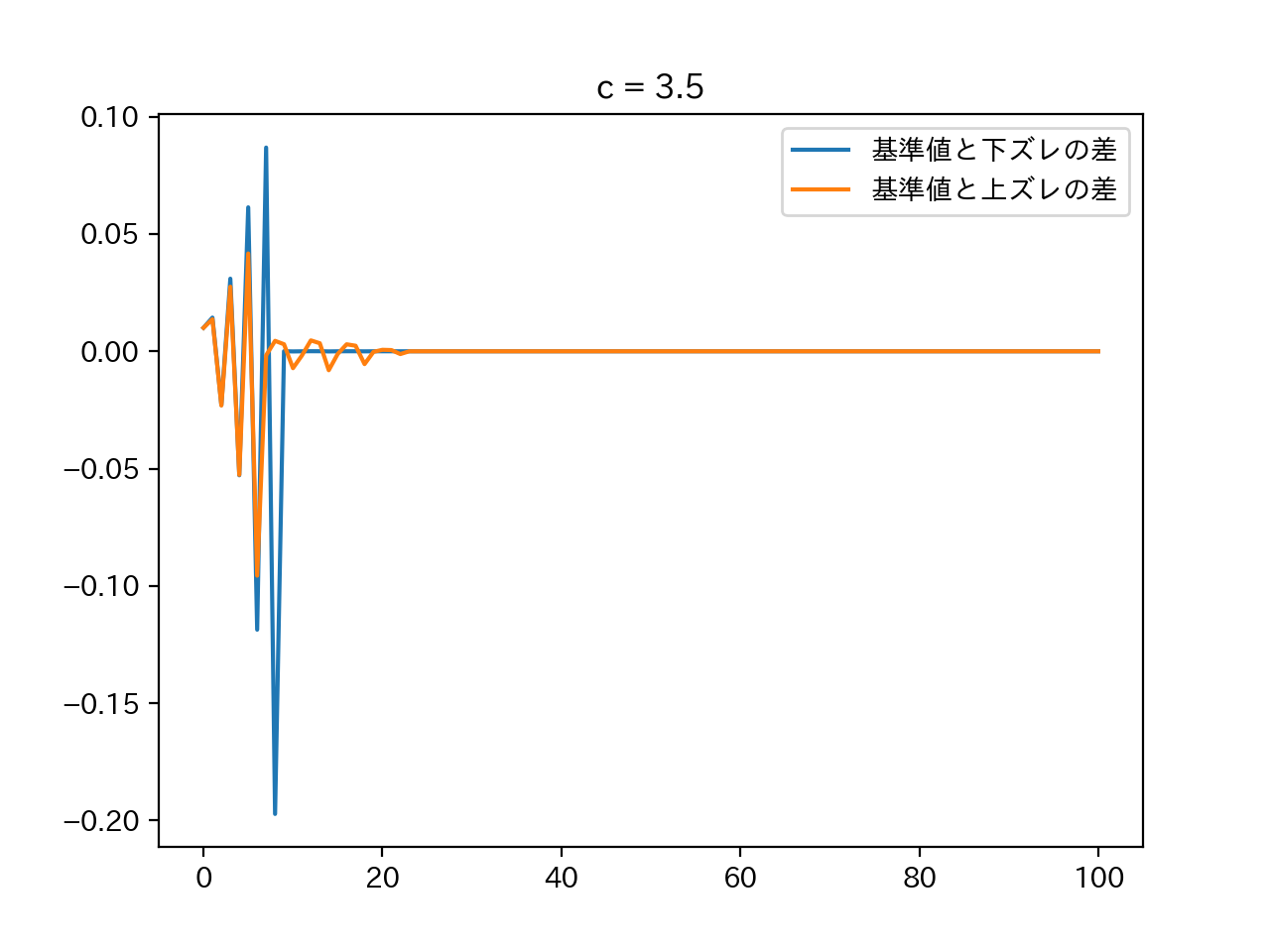
せっかくグラフにしたのに見づらいですね。基準となる初期値を基準値と呼び、基準値から下にズレた初期値(下ズレ)と基準値から上にズレた初期値(上ズレ)の差分を取ります。
最初の数年こそ初期値の影響を受けていますが、途中からはピッタリと重なっています。初期値が少しズレていてもあまり影響が無いことがわかります。
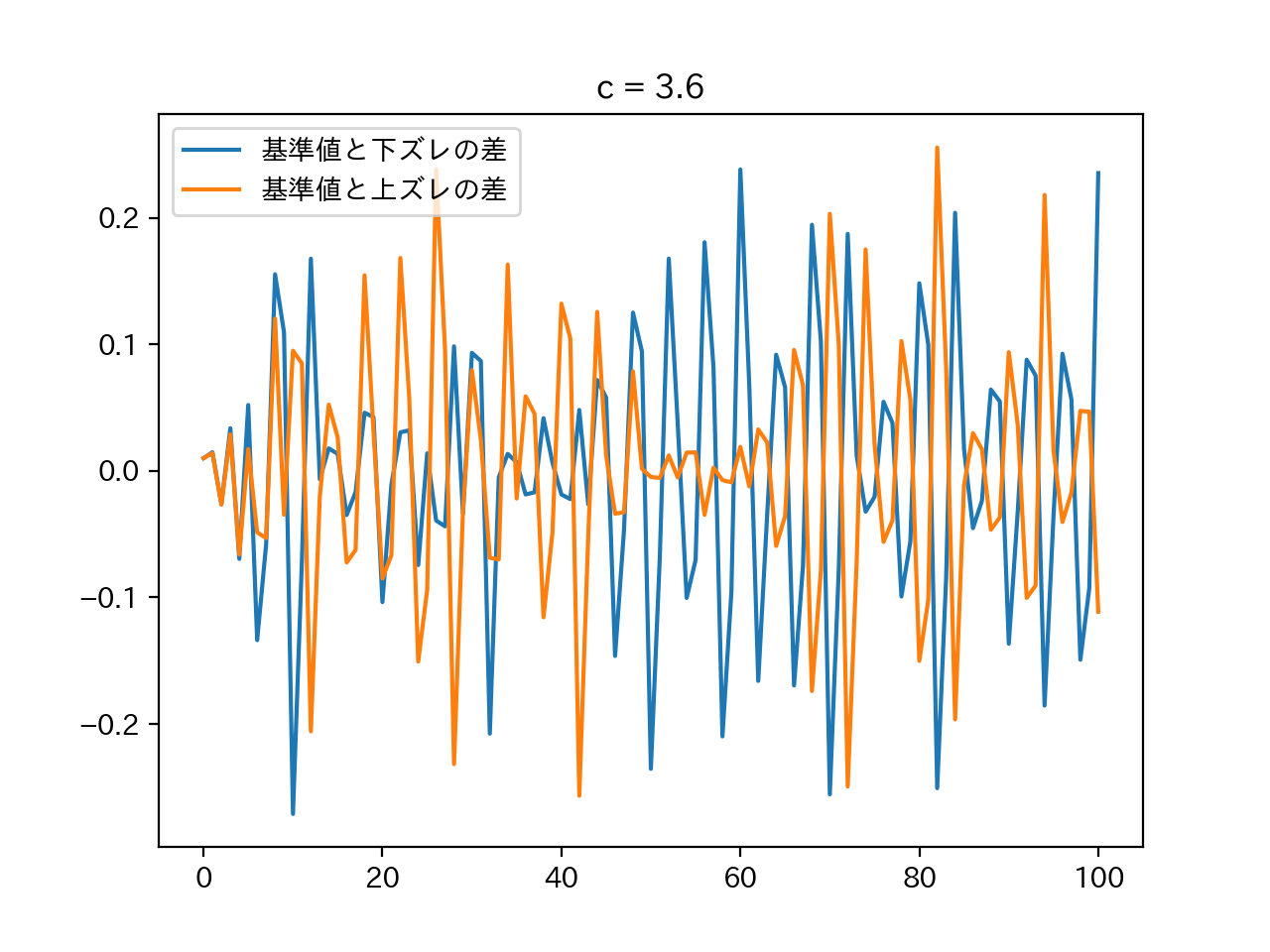
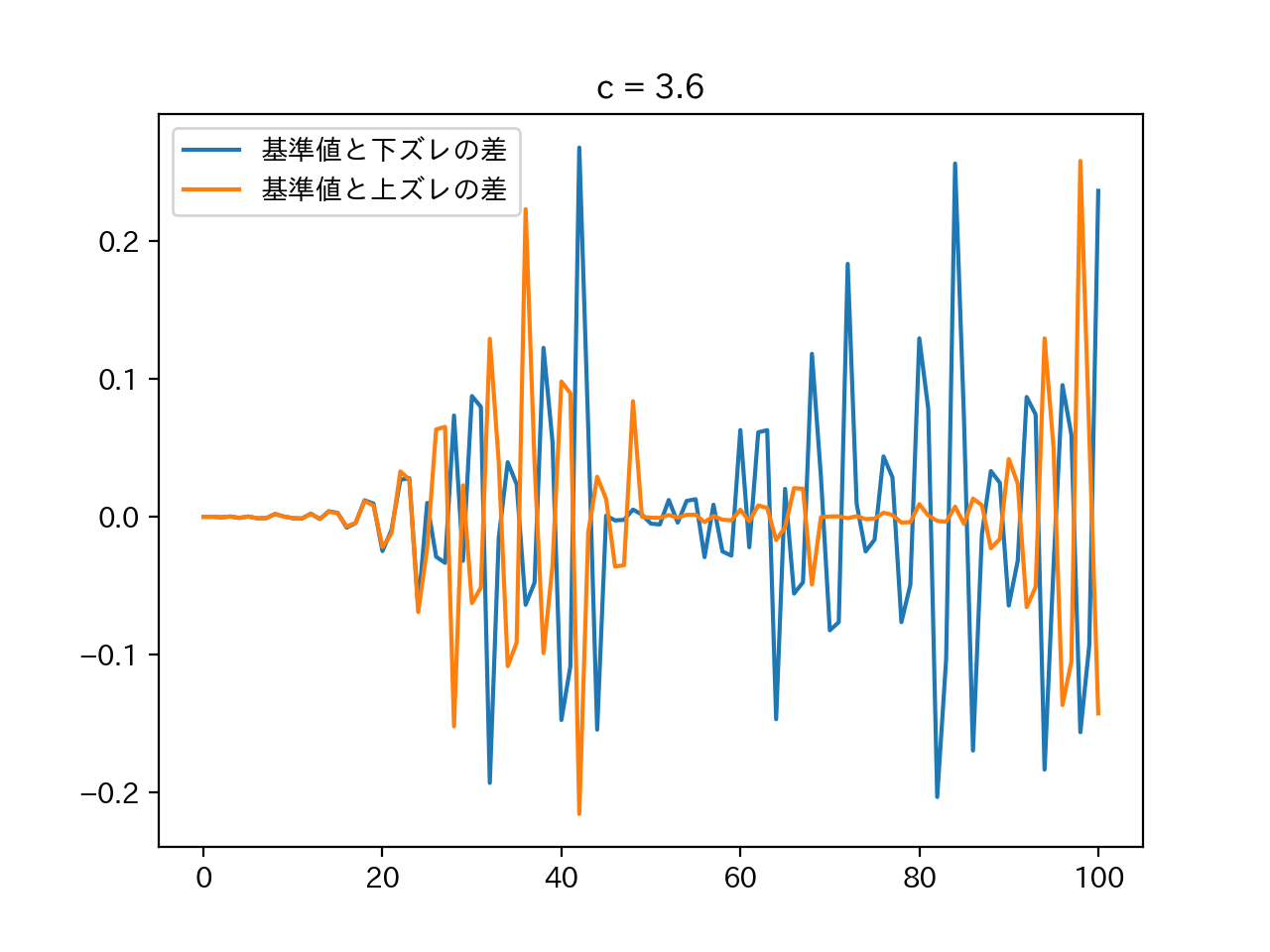
c = 3.6のとき (カオス)
それではカオスである$c = 3.6$のグラフを見てみましょう。中二病の名前も相まって結果を見るのが少しワクワクします。
なんかキレイですね!カオスアートとかどうですか。
緑の線の後ろでオレンジと青い線がにじみ出ているのが見えますが、これも差分をとってわかりやすくしましょう。
めちゃめちゃわかりやすくカオスですね。
初期値のズレが更に小さい時
初期値のズレをさらに小さくするとカオスが発生するまでの時間は長くなりますが、それでもカオスは生まれます。下のグラフは初期値の比較として$3±0.0001$を使用しています。
カオスが始まったかと思いきや、途中で再びシンクロしだすところ(50年目あたり)がいかにもカオスですね。
まとめ
- 単純な規則からカオスが生まれることを確認した
- カオスにおける初期値敏感性を確認した
余談
人生で一番カオスと書いた。
余談1: カオス理論に出会うまでの経緯
僕が応援している浦和レッズの分析官に林舞輝さんが就任することになりました。彼は戦術的ピリオダイゼーションという複雑系やカオス理論を応用したサッカーの理論にくわしく、僕も詳しくなりたいなと思っていろいろ探していたところ香川大レポジトリにある上述の論文に出会いました。戦術的ピリオダイゼーションを初学者でも分かるように説明してくれているので、詳細を知りたい方には超おすすめです。(カオス理論といえば『ジュラシック・パーク』ですね。ジェフ・ゴールドブラムは194cm)
余談2: 「バタフライ・エフェクト」
日本流にいうと「風が吹けば桶屋が儲かる」が近いですが、論理性の有無が異なります。「風が吹けば桶屋が儲かる」は風が吹いてから桶屋が儲かるまでの流れに(無理やりな部分はあれど)論理が存在しますが、「バタフライ・エフェクト」は蝶々の羽ばたきがどのようにテキサスの竜巻に影響を与えるかの論理的なつながりを知ることができません。(『バタフライ・エフェクト』いい映画ですよね。アシュトン・カッチャー)
余談3: ロジスティックス写像の係数
ロジスティックス写像の係数と合計特殊出生率のアナロジーが正しい自信がないので、出生率うんぬんのところは話半分で読んでください。
「人口維持」に必要な合計特殊出生率は理論的には2(早死を加味すると実際はもう少し上)が必要です。ここでの「人口維持」とは$X$が初期値のままずっと変わらないことを指し、ロジスティックス写像では、例えば初期値0.5で係数2のときに「人口維持」の状態になります(下図参照)。
余談4: 人口が極限まで増えた結果、人類は滅亡した
フィクションです。世界の特殊出生率を見ると4を超えている国は多いので、現実世界はカオスだけでは説明しきれなっかたり、滅亡するまでに時間がかかっていたり、そもそもカオスと特殊出生率の比較が正しくなかったりするんでしょうね。