サッカーにおけるオフサイド

サッカーで論争を呼ぶ話題として最も多いのはPK問題とならんでオフサイド問題ではないでしょうか。
サッカーの得点シーンをめぐり避けることができないのが、いまのオフサイドでしょ問題。SNS上の動画・静止画を使って、TV中継のリプレイさながら、仮想のオフサイドラインを引くことが簡単な時代になりました。そのとき、問うべきは

「そのオフサイドライン、本当に正しいの？」

なぜなら直感的に私たちが引くオフサイドラインは往々にして少し間違っているからです。これは3次元のモノ（ピッチ、選手、ボールなど）を2次元空間（映像・写真）に閉じ込めた（変換した）弊害です。解決策としては以下の2つがあります。

３D空間でリプレイを見る（VRなどを使う）
2次元で作図するときにできるだけ歪まないようにする

３D空間でのリプレイ体験はそちらの開発者に任せるとして、今回注目するのは正しい作図です。

消失点とは

今回キーとなる消失点について簡単に説明します。

私達は基本的に3次元のモノを2次元に投影して理解しています。その3次元から2次元への変換の際に生じる「ゆがみ」の結果生まれるものが消失点となります。永遠に続く平行な直線は一点で交わっているように見え、遠くにいる人は小さく見れるようになります。

なぜ消失点を求めることが大事なのかは「消失点絶対求めるマンの第一人者」こと、かつー様の記事を参照するのが最も分かりやすいと思うので是非参照ください。
とりあえず(http://blog.livedoor.jp/sgjk22/archives/42696576.html)

消失点絶対求めるマン

消失点絶対求めるマンとは、

消失点を求めずに引かれたオフサイドラインをみるとムズムズする
「消失点求めてから引けよ…」と独り言をつぶやく
そしてペイントを起動する
「消失点」でゲシュタルト崩壊している

人たちの総称です。

この記事の目的

消失点の求め方を定式化・自動化することによって、消失点（絶対求めるマン）普及の一助となること。

モデル化のために

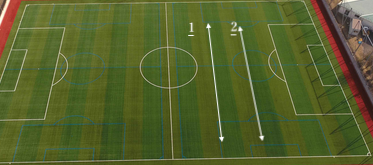
消失点はピッチの縞模様を使って４点から２つの直線を引くことで求めることができます。（２直線が並行であることが前提ですが）
ここで、消失点を求めるということは２直線の交点を求めることに他なりません。

下は「消失点絶対殺すマン」殺しのピッチ（こんな芝目のときあったっけ）

簡単な例

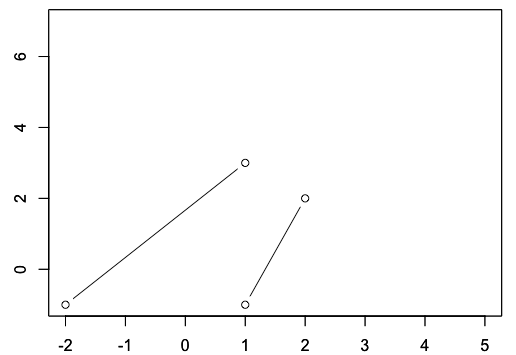
4点$A,B,C,D$を使って消失点を求めてみます。
$A=(1,3),B=(-2,-1),C=(2,2),D=(1,-1)$とし、$AB$間,$CD$間で線分を引きます。

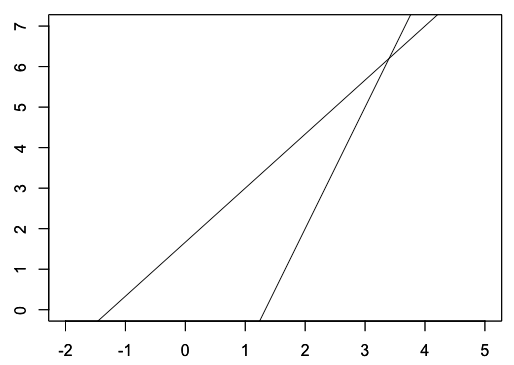
この線分を直線に拡張したときの交点が消失点となるわけです

中学生的解決

点A,Bと点C,Dから直線の式をそれぞれ求めて、それら２つの直線の式の連立方程式を解くことによって交点を求めます。
直線の式（１次式）は
$y=mx+b$
で表すことができ、２点の座標を$A=(A_x,A_y),B=(B_x,B_y)$とすると傾き$m$,切片$b$を求めるには、まず傾きを求め、
$m=\frac{A_y-B_y}{A_x-B_x}$
それを使い、下の式をまとめることによって切片を得ます。
$y=m(x-A_x)+A_y$

例題の例

中学数学の復習

$A=(1,3),B=(-2,-1)$

傾きを求める

$m=\frac{3-(-1)}{1-(-2)}=\frac{4}{3}$

切片を求める(直線の式を求める)

(1) $y=m(x-1)+3=\frac{4}{3}x+\frac{5}{3} $

$C=(2,2),D=(1,-1)$ についても同様に求める。

(2) $y=3x-4$

(1),(2)式の連立方程式を求めると

$x=\frac{17}{5}, y=\frac{31}{5}$

問題点

全ての直線を表現できません。
具体的には2点のx座標が等しい時に傾きを求めることができません。たとえば$A_x=B_x=c$となる場合、傾きの分母がゼロになるため計算ができなくなります。手計算なら$x=c$の形で書けますが、自動化の計算をするにはif文での分岐など構造を少しでも複雑にしなければいけません。

解決策

解決策は超シンプルで、直線の式の分母を払うことです。交点を求める際の行列の要素として使うので、分母を払った後の式については「一般化と高校生的解決」欄で解説します。

一般化と高校生的解決

点の集合が${a_1,...,a_4}$で与えられており、$i$番目の点とその座標を$a_i=(x_i,y_i)$で表すとします。このとき直線の式は、上で出てきた直線の式の分母を払ったものとなり、下の式で表せます。($i=1,3$なので$i+1=2,4$)

$-(y_i-y_{i+1})x+(x_i-x_{i+1})y=(x_i-x_{i+1})y_i-(y_i-y_{i+1})x_i$

上の式に$\Delta x=x_i-x_{i+1},\Delta y=y_i-y_{i+1}$を導入すると、下のように式を簡略化できます。

$-(\Delta y)x+(\Delta x)y=(\Delta x)y_i-(\Delta y)x_i$

ここに$x_i,x_{i+1},y_i,y_{i+1}$を代入することによって直線の式を求めることができます。

行列化

連立1次方程式は傾きに関する行列と切片に関するベクトル、変数ベクトルを設定することにより

$ A \underline{x} = \underline{b} $

で表せます。上の例では下のようになります。

 A = \left(
    \begin{array}{cc}
      -\Delta y_1 & \Delta x_1 \\
      -\Delta y_3 & \Delta x_3
    \end{array}
  \right)

\underline{b} = \left(
    \begin{array}{c}
      \Delta x_1 \dot{} y_1 - \Delta y_1 \dot{} x_1 \\
      \Delta x_3 \dot{} y_3 - \Delta y_3 \dot{} x_3 
    \end{array}
  \right)

\underline{x} = \left(
    \begin{array}{c}
      x \\
      y
    \end{array}
  \right)

未知の$x$を求めるために、普通の1次式なら両辺をAで割ればいいのですが、行列の計算では割り算の代わりに逆行列を掛けます。
逆行列が存在するような行列を正則な行列と呼びます。

下のような行列$B$が与えられたとき、行列式$D$は$ad-bc$となり、これが非ゼロなときに$B$の逆行列は存在します。

 B = \left(
    \begin{array}{cc}
      a & b \\
      c & d
    \end{array}
  \right)

今回の例では
$D=-\Delta y_1\dot{}\Delta x_3 + \Delta y_3 \dot{} \Delta x_1 \neq 0$
となるような$D$であればOKです。

2つの直線が並行になる場合、行列式はゼロになります。ここはif文で分岐が必要なところです。

$ x = A^{-1}b $ を解いて$x$を求める。逆行列$A^{-1}$は

 A^{-1} = \frac{1}{ad-bc}\left(
    \begin{array}{cc}
      \Delta x_3 & -\Delta x_1 \\
      \Delta y_3 & -\Delta y_1
    \end{array}
  \right)

なので

 \underline{x} = \frac{1}{ad-bc}\left(
    \begin{array}{cc}
      \Delta x_3 & -\Delta x_1 \\
      \Delta y_3 & -\Delta y_1
    \end{array}
  \right)
  \left(
    \begin{array}{c}
      \Delta x_1 \dot{} y_1 - \Delta y_1 \dot{} x_1 \\
      \Delta x_3 \dot{} y_3 - \Delta y_3 \dot{} x_3 
    \end{array}
  \right)

で交点$\underline{x}$が求まります。

任意の点へ線を引っ張る

サッカーの場合においてはオフサイドラインの基準となる選手が任意の点として使われることが多い。

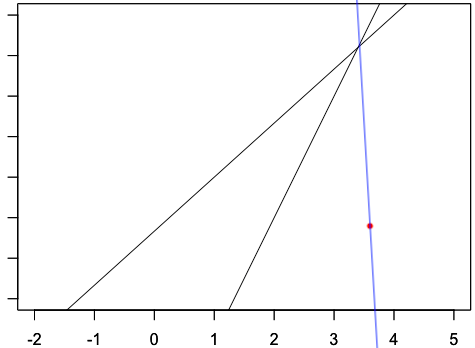
まとめ

黒線同士の交点が消失点で、赤点が任意の点（サッカーではオフサイドラインの選手）

課題

消失点を求めるときにずっともやもやしていたのが、「選手の背の高さって無視していいの？」っていうこと。今回求めた消失点はピッチレベル（高さ$z=0$）ですが、オフサイドラインは「一番ゴールラインに近い体の部位」を基準に引かれます。（オフェンスの選手のオフサイド判定部位はまた違うので注意）例えば、DFの手(例：z=100cm)をオフサイドラインの基準にすると、ピッチレベルにある消失点から、高さ100cmのところにあるDFの手に向かって斜めの線が引かれるわけです。これを2次元空間に変換してみると、若干ではありますが正しくないオフサイドラインが引けるはずです。「パッと見では気づかないレベルの違いを可視化しましょう」というのが消失点を求める目的の１つなので、どうせならこういうところもきっちりしたいです。

参考：17/18 競技規則 (https://www.jfa.jp/documents/pdf/soccer/lawsofthegame_201718.pdf)90ページくらいから
（DFのオフサイドライン判定部位については明記されていない気がするのですが、どうでしょうか
読みが甘いだけかもしれませんが）

高さに関するデータを取り入れます。オフサイドラインの基準となる選手の体の部位が分かればある程度の高さは予測できます。その部位とピッチレベルにある消失点を結ぶことで、より正確なオフサイドラインを引くことができるはずです。

数式としては、上で使った2次元での直線の式を3次元に拡張してあげるとよいです。平面の式を使って、そのあと高さを限定したほうが式的にはシンプルかもしれません。時間があればチャレンジしたいところです。

実際3次元への拡張がどれだけ現実的で効果のある話なのかはわかりません。

この記事をきっかけにサッカーに興味を持つ人がいれば幸いです。中学・高校レベルの簡単な数学でこんなことができるんだなと知っていただければ幸いです。

【サッカー】オフサイドを数学的に見る - 消失点絶対求めるマンのための数学