はじめに
前回、Human Activity Recognition with SmartphonesとCNNを使って分類問題を解きました。センサーデータから得られた561個の特徴量を固定長のシーケンスに見立てましたが、実際の問題だとシーケンス長が固定じゃない場合が多そうだなと思い、可変長データの分類をやってみようと思います。
ただ、可変長のデータセットがうまく見つからなかったので、適当にデータを作り、それを分類するという自作自演になってしまいました…。
とりあえずやったことの紹介
sinとcosをベースに適当に振幅を変えたり、ノイズを加えたりして、3種類のデータを作りました。
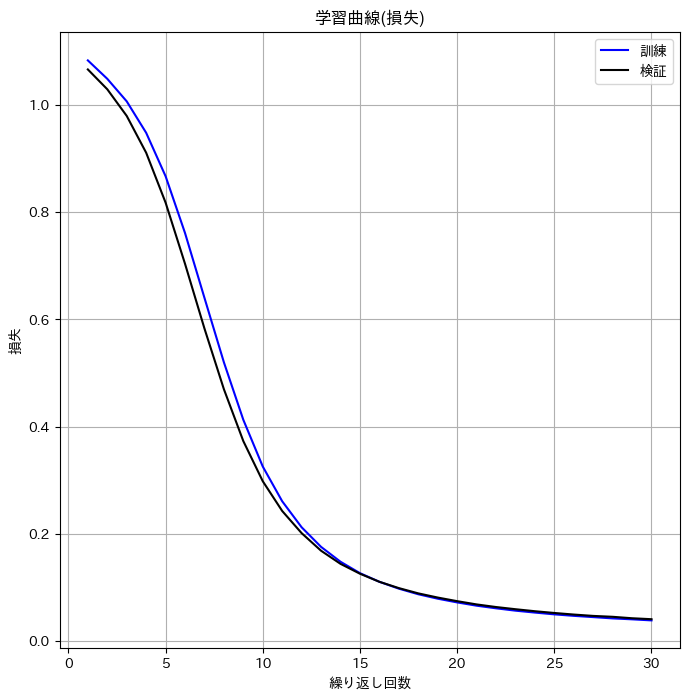
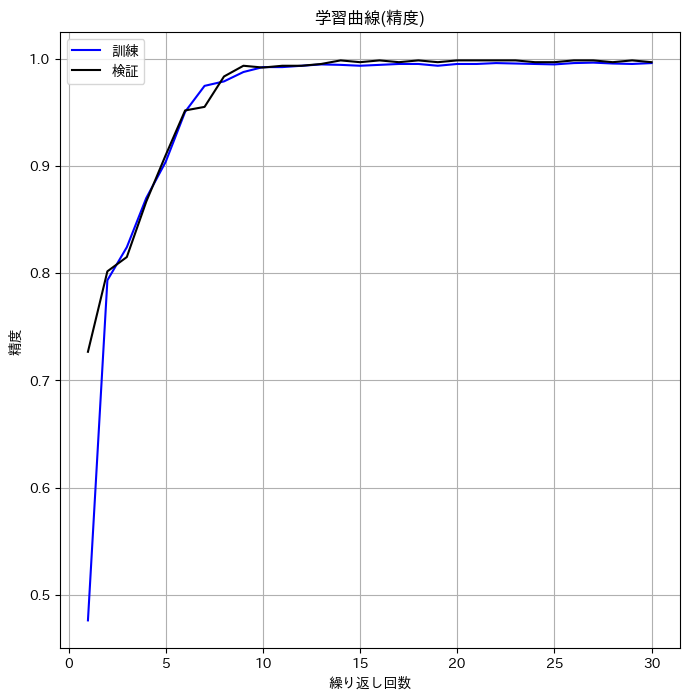
CNNは前回とほぼ同じです。ただ、可変長シーケンスに対応するため、細かいところを修正しなければならず、苦労しました。学習曲線は以下の通りで、初期の学習がうまく進んでいませんが、お許しください(誰にw?)。
初期状態: 損失: 1.06633 精度: 0.72667
最終状態: 損失: 0.04075 精度: 0.99667
そもそもデータが適当なので、正解率などの数値は参考程度かと思います。個別の予測結果(の一部)を図示すると以下のような感じです。タイトル欄にある左側の数字は正解ラベル、右側が予測値です。上の図の赤い線が0、青い線が1、緑の線が2です。
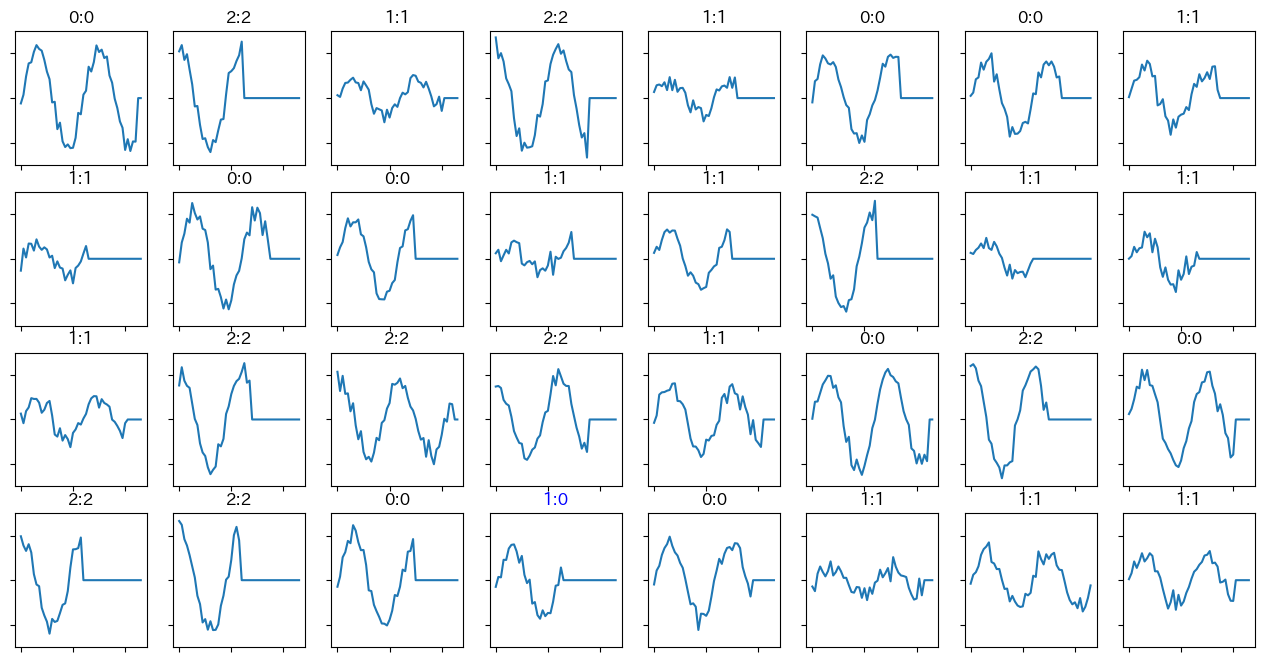
4行4列目が予測を外していますが、これは人の目で見ても間違えそうです。正解が1なので、本来は振幅がもっと小さいはずですが、乱数の影響でたまたま振幅が大きくなってしまったようです。ちなみに、波形の右側が平らになっているのは、元のデータが可変長だからです。0埋めされています。
ライブラリをインポート
では、実装です。
import numpy as np
import random
from tqdm.notebook import tqdm
# torch
import torch
import torch.nn as nn
import torch.optim as optim
from torch.utils.data import DataLoader, Dataset, random_split
# sklearn
from sklearn.metrics import accuracy_score
# matplotlib
import matplotlib.pyplot as plt
%matplotlib inline
import japanize_matplotlib
# warnings
import warnings
warnings.filterwarnings('ignore')
準備
乱数固定や定数の設定、GPUのチェックを行います。
SEED = 123
def seed_everything(seed=42):
random.seed(seed)
#np.random.seed(seed)
np.random.RandomState(seed)
# os.environ['PYTHONHASHSEED'] = str(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.Generator().manual_seed(seed)
torch.backends.cudnn.daterministic = True
torch.use_deterministic_algorithms = True
# torch.backends.cudnn.benchmark = False
seed_everything(SEED)
# データ生成
subject = 1000
min_seq_len = 24
max_seq_len = 48
num_channel = 1
num_class = 3
# 訓練
batch_size = 32 # バッチサイズ
n_hidden = 16 # 全結合層の隠れ層のノード数
lr = 0.0002 #0.0001 # 学習率
num_epochs = 30 # 30 # エポック数
device = torch.device("cuda:0" if torch.cuda.is_available() else "cpu")
print(device)
データ生成
データを作成します。今回3種類の波形データを作ります。sinやcosに適当な振幅を掛け、ノイズを加えただけです。
def wave_0(T):
a = np.random.uniform(0.8, 1.2)
return [(a*np.sin(t))+(np.random.randn()/8) for t in T]
def wave_1(T):
a = np.random.uniform(0.3, 0.7)
return [(a*np.sin(t))+(np.random.randn()/8) for t in T]
def wave_2(T):
a = np.random.uniform(0.8, 1.2)
return [(a*np.cos(t))+(np.random.randn()/8) for t in T]
3種類の波形を1000通り、合計3000個のデータを作成しました。
X = []
y = []
seq_lengths = []
for i in range(subject):
seq_len = np.random.randint(min_seq_len, max_seq_len)
T = np.linspace(0, 2*2*np.pi, max_seq_len+1)[:seq_len]
# wave_0
X.append(np.array(wave_0(T)).reshape(num_channel, -1)) # (channel, sequence_length)
y.append(0)
seq_lengths.append(seq_len)
# wave_2
X.append(np.array(wave_1(T)).reshape(num_channel, -1))
y.append(1)
seq_lengths.append(seq_len)
# wave_3
X.append(np.array(wave_2(T)).reshape(num_channel, -1))
y.append(2)
seq_lengths.append(seq_len)
print(f"""
X length: {len(X)},
y length: {len(y)},
sequence lenght: {len(seq_lengths)}
""")
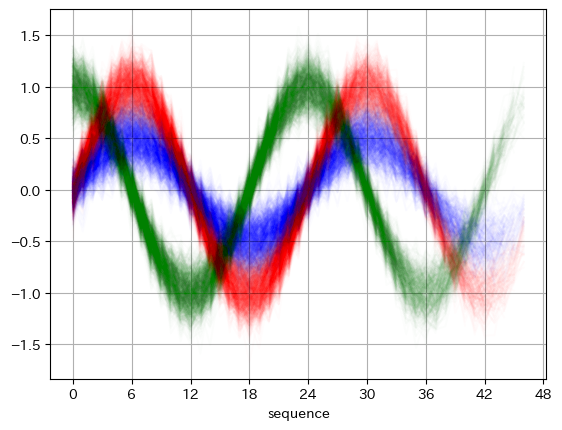
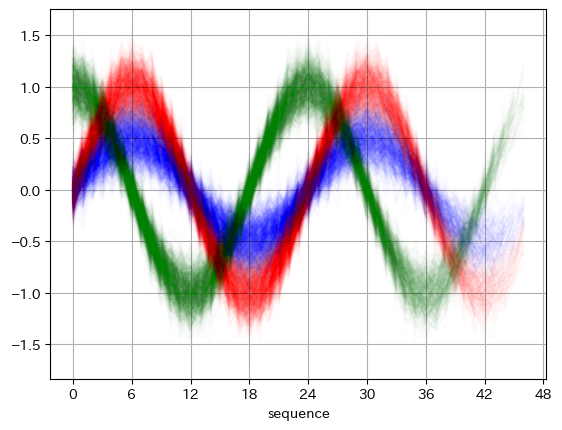
作成した波形データをプロットすると以下のようになります。赤い線がwave_0、青い線がwave_1、緑の線がwave_2です。今回シーケンス長を24~48にしたので、線は途中で途切れてます。後半につれ、線の色が薄くなっているのはそのためです。
# 可視化
for i, label in enumerate(y):
if label==0: plt.plot(X[i][0], alpha=0.01, color='red')
elif label==1: plt.plot(X[i][0], alpha=0.01, color='blue')
elif label==2: plt.plot(X[i][0], alpha=0.01, color='green')
plt.xticks(np.linspace(0, max_seq_len, 9))
plt.xlabel('sequence')
plt.grid()
plt.show()
データローダーを作成
データローダーを作ります。
# データセットクラスを定義
class TimeSeriesDataset(Dataset):
def __init__(self, data, labels):
self.data = [torch.tensor(d, dtype=torch.float32) for d in data]
self.labels = torch.tensor(labels, dtype=torch.long)
def __len__(self):
return len(self.labels)
def __getitem__(self, idx):
return self.data[idx], self.labels[idx]
# インスタンス化
dataset = TimeSeriesDataset(X, y)
print(len(dataset))
3000
(繰り返しになりますが)今回のデータは可変長なので、シーケンス長をそろえるための関数を定義します。このあたりは生成AIに相談しながら実装したので、もっと良い解法があるのかもしれません…。
# 可変シーケンス対応
# パディングを適用してすべてのシーケンスを同じ長さにする関数
def pad_collate_fn(batch):
max_length = max([x[0].shape[1] for x in batch])
#print(f"max_length: {max_length}")
padded_data = []
labels = []
for data, label in batch:
# シーケンスの最後に0を追加してパディング
#print(data.shape)
#print(data[0])
padded_seq = nn.functional.pad(data, (0, max_length - data.shape[1], 0, 0)) # (channels, padding_length)
padded_data.append(padded_seq)
labels.append(label)
return torch.stack(padded_data), torch.tensor(labels)
# 訓練用と検証用に分割する
train_size = int(len(dataset) * 0.8)
val_size = len(dataset) - train_size
train_dataset, val_dataset = random_split(dataset, [train_size, val_size])
# データローダーを作成
train_loader = DataLoader(train_dataset, batch_size=batch_size, shuffle=True, collate_fn=pad_collate_fn)
val_loader = DataLoader(val_dataset, batch_size=batch_size, shuffle=False, collate_fn=pad_collate_fn)
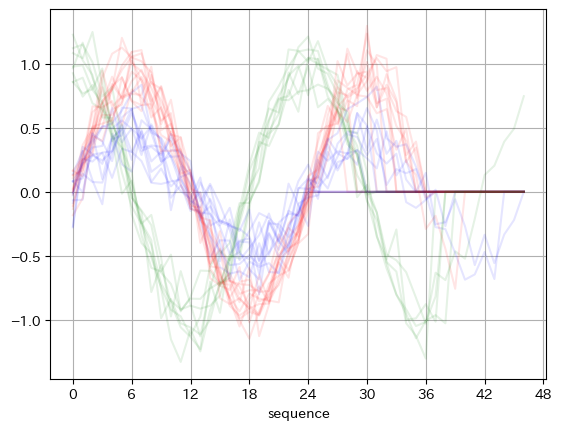
データローダーから最初の1バッチを取り出し、グラフ化します。
# 最初の1セットを取り出し、可視化
for X_train, y_train in train_loader:
break
plt.figure()
for i, label in enumerate(y_train):
if label==0: plt.plot(X_train[i][0], alpha=0.1, color='red')
elif label==1: plt.plot(X_train[i][0], alpha=0.1, color='blue')
elif label==2: plt.plot(X_train[i][0], alpha=0.1, color='green')
plt.xticks(np.linspace(0, max_seq_len, 9))
plt.xlabel('sequence')
plt.grid()
plt.show()
シーケンス方向のパディングは出来てそうですし、大丈夫な気がします。
関数を定義
訓練に入る前に、必要な処理を関数化しておきます。
def eval_loss(loader, device, net, criterion):
"""
損失関数を計算するための関数
Parameters
----------
loader: torch.utils.data.dataloader.DataLoader
データローダー
device: torch.device
テンソルをどのデバイスに割り当てるか(cuda:0, cpu)
net:
学習ネットワーク
criterion:
損失関数(交差エントロピー誤差など)
Return
---------
loss:
損失値
"""
# データローダーから最初の1セットを取得する
for images, labels in loader:
break
# デバイスの割り当て
inputs = images.to(device)
labels = labels.to(device)
# 予測計算
outputs = net(inputs)
# 損失計算
loss = criterion(outputs, labels)
return loss
def fit(net, optimizer, criterion, num_epochs, train_loader, val_loader, device, history):
"""
分類問題に対する訓練用の関数。base_epochsを設定することで、追加訓練ができるようになっている。
Parameters
-------------
net:
訓練ネットワーク
optimizer:
最適化手法(SGD, Adamなど)
criterion:
損失関数(交差エントロピー誤差など)
num_epochs: int
エポック数
train_loader: torch.utils.data.dataloader.DataLoader
訓練用のデータローダー
val_loader: torch.utils.data.dataloader.DataLoader
検証用のデータローダー
device:
テンソルを割り当てるデバイス(cpu, cuda:0)
history:
訓練&検証結果が格納された配列。最初の訓練の場合は空の配列。例: (エポック数, 訓練損失, 訓練精度, 検証損失, 検証精度)
Returns
--------------
history:
今回の訓練&検証結果を追加した配列
"""
# 既に訓練済みのエポック数
base_epochs = len(history)
# 訓練
for epoch in range(base_epochs, num_epochs+base_epochs):
n_train_acc, n_val_acc = 0, 0 # 1エポックあたりの正解数(精度計算用)
train_loss, val_loss = 0, 0 # 1エポックあたりの累積損失(平均化前)
n_train, n_val = 0, 0 # 1エポックあたりのデータ累積件数
#訓練フェーズ
net.train()
for inputs, labels in tqdm(train_loader):
# データ件数
train_batch_size = len(labels) # 1バッチあたりのデータ件数
n_train += train_batch_size # データ累積件数
# デバイス(cpu, gpu)に割り当てる
inputs = inputs.to(device)
labels = labels.to(device)
# 勾配の初期化
optimizer.zero_grad()
# 予測計算
#print(inputs.shape, labels.shape)
outputs = net(inputs)
# 損失計算
loss = criterion(outputs, labels)
# 勾配計算
loss.backward()
# パラメータ修正
optimizer.step()
# 予測ラベル導出
predicted = torch.max(outputs, 1)[1]
# 平均前の損失と正解数の計算
# lossは平均計算が行われているので平均前の損失に戻して加算
train_loss += loss.item() * train_batch_size
n_train_acc += (predicted == labels).sum().item()
#予測フェーズ
net.eval()
for inputs_val, labels_val in val_loader:
# データ件数
val_batch_size = len(labels_val) # 1バッチあたりのデータ件数
n_val += val_batch_size # データ累積件数
# GPUヘ転送
inputs_val = inputs_val.to(device)
labels_val = labels_val.to(device)
# 予測計算
outputs_val = net(inputs_val)
# 損失計算
loss_val = criterion(outputs_val, labels_val)
# 予測ラベル導出
predict_val = torch.max(outputs_val, 1)[1]
# 平均前の損失と正解数の計算
# lossは平均計算が行われているので平均前の損失に戻して加算
val_loss += loss_val.item() * val_batch_size
n_val_acc += (predict_val == labels_val).sum().item()
# 精度計算
train_acc = n_train_acc / n_train
val_acc = n_val_acc / n_val
# 損失計算
avg_train_loss = train_loss / n_train
avg_val_loss = val_loss / n_val
# 結果表示
print (f'Epoch [{(epoch+1)}/{num_epochs+base_epochs}], tr_loss: {avg_train_loss:.5f} tr_acc: {train_acc:.5f} val_loss: {avg_val_loss:.5f}, val_acc: {val_acc:.5f}')
# 記録
item = np.array([epoch+1, avg_train_loss, train_acc, avg_val_loss, val_acc])
history = np.vstack((history, item))
return history
def check_history(history):
"""
historyを確認するための関数
Parameters
------------------
history: np.array: (繰り返し数, 訓練損失, 訓練精度, 検証損失, 検証精度)
訓練結果が格納されたnumpy配列
Return
------------------
None
Display
------------------
訓練開始時の損失&精度と、訓練終了時の損失&精度
損失に関する学習曲線
精度に関する学習曲線
"""
#損失と精度の確認
print(f'初期状態: 損失: {history[0,3]:.5f} 精度: {history[0,4]:.5f}')
print(f'最終状態: 損失: {history[-1,3]:.5f} 精度: {history[-1,4]:.5f}' )
num_epochs = len(history)
ticks_interval = 5 #num_epochs // 10
# 学習曲線の表示 (損失)
plt.figure(figsize=(8,8))
plt.plot(history[:,0], history[:,1], 'b', label='訓練')
plt.plot(history[:,0], history[:,3], 'k', label='検証')
plt.xticks(np.arange(0, num_epochs+1, ticks_interval))
plt.xlabel('繰り返し回数')
plt.ylabel('損失')
plt.title('学習曲線(損失)')
plt.legend()
plt.grid()
plt.show()
# 学習曲線の表示 (精度)
plt.figure(figsize=(8,8))
plt.plot(history[:,0], history[:,2], 'b', label='訓練')
plt.plot(history[:,0], history[:,4], 'k', label='検証')
plt.xticks(np.arange(0, num_epochs+1, ticks_interval))
plt.xlabel('繰り返し回数')
plt.ylabel('精度')
plt.title('学習曲線(精度)')
plt.legend()
plt.grid()
plt.show()
問題特有のパラメータ
in_channel = num_channel
sequence_length = max_seq_len-1
n_output = num_class
# 表示
print(f'in_channel: {in_channel}, sequence_length: {sequence_length}, n_output: {n_output}')
in_channel: 1, sequence_length: 47, n_output: 3
モデル作成
モデルを定義します。畳み込み層が2つ、活性化関数はReLU、プーリング層にはAdaptive Max Poolingを使います。最初は全結合層を2層にしていたのですが、学習が早く終わりすぎてしまったので、1層に減らしました。
class CNN(nn.Module):
def __init__(self, in_channel, sequence_length, n_hidden, n_output):
super().__init__()
self.conv1 = nn.Conv1d(in_channel, 16, kernel_size=3, stride=1, padding=1)
self.conv2 = nn.Conv1d(16, 32, kernel_size=3, stride=1, padding=1)
self.relu = nn.ReLU(inplace=True)
#self.maxpool = nn.MaxPool1d(kernel_size=2, stride=2)
self.adpool = nn.AdaptiveMaxPool1d(1) # 最後のプーリング層
self.flatten = nn.Flatten()
#self.l1 = nn.Linear(64*(sequence_length//2), n_hidden)
self.l1 = nn.Linear(64, n_hidden)
self.l2 = nn.Linear(n_hidden, n_output)
self.l3 = nn.Linear(32, n_output)
self.features = nn.Sequential(
self.conv1,
self.relu,
self.conv2,
self.relu,
self.adpool
)
self.classifier = nn.Sequential(
# case 1
# self.l1,
# self.relu,
# self.l2
# case 2
self.l3
)
def forward(self, x):
x1 = self.features(x)
x2 = self.flatten(x1)
x3 = self.classifier(x2)
return x3
損失関数は交差エントロピー誤差、最適化手法はAdamです。
# インスタンス作成
net = CNN(in_channel, sequence_length, n_hidden, n_output).to(device)
# 損失関数
criterion = nn.CrossEntropyLoss() # 交差エントロピー誤差
# 最適化関数と学習率
optimizer = optim.Adam(net.parameters(), lr=lr)
訓練
訓練と検証を行います。
# 訓練&検証結果記録用の配列
history = np.zeros((0, 5)) # (繰り返し数, 訓練損失, 訓練精度, 検証損失, 検証精度)
history = fit(
net=net,
optimizer=optimizer,
criterion=criterion,
num_epochs=num_epochs,
train_loader=train_loader,
val_loader=val_loader,
device=device,
history=history
)
学習曲線
学習曲線を表示させます。
check_history(history)
初期状態: 損失: 1.06633 精度: 0.72667
最終状態: 損失: 0.04075 精度: 0.99667
初期段階の学習がうまく進んでおらず、損失の減少ペースが緩やかなのが気になりますが、とりあえずコードは実行できました。今回、検証データと訓練データの分割はちゃんとできていない(そもそもデータ自体が適当に自作したもの…)ので、過学習についてはわかりませんでした。
予測結果
予測結果を見てみます。検証データを使って、波形と正解ラベルと予測ラベルを表示します。
# 可視化
for inputs_val, labels_val in val_loader:
# GPUヘ転送
inputs_val = inputs_val.to(device)
labels_val = labels_val.to(device)
# 予測計算
outputs_val = net(inputs_val)
predicts_val = torch.max(outputs_val, 1)[1]
plt.figure(figsize=(16, 8))
for i in range(batch_size):
y_pred = predicts_val[i]
y_true = labels_val[i]
ax = plt.subplot(4, 8, i+1)
ax.tick_params(labelbottom=False, labelleft=False, labelright=False, labeltop=False)
plt.plot(inputs_val[i][0].cpu())
plt.ylim(-1.5, 1.5)
if y_pred == y_true:
c = 'k'
else:
c = 'b'
plt.title(f"{y_true}:{y_pred}", color=c)
plt.show()
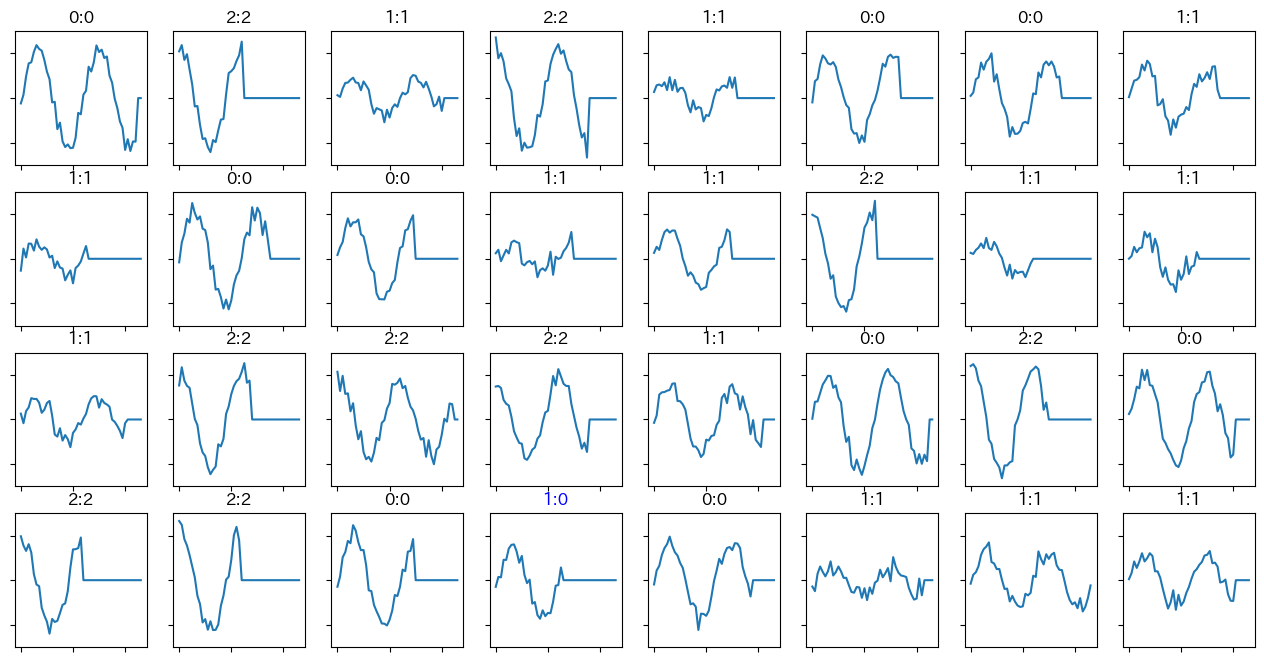
タイトル欄にある左側の数字が正解ラベルで、右側の数字が予測ラベルです。4行4列目のデータは予測が外れています。が、これは人の目で見ても間違えそうな気がします。理由は冒頭に書いたので、割愛。
おわりに
可変シーケンスのデータをCNNで分類する問題に取り組みました。いい感じのデータが見つからず、データを自作するところから始めたため、精度に関してはわかりませんが、とりあえず実装は出来たような気がしています。