S-learnerとDDMLの比較: 正則化バイアスの抑制

概要

• Meta-learnerの枠組みは「ITEとATEが一貫した値で得られる（S, T, X-learnerなど）」という点で大きな実用価値があると考えているが、「正則化バイアスや過適合が発生しやすい」という危険性もある。
• この危険性を抑制する手法として、DDML（Double Debiased Machine Learning）がある。本当にバイアス・過適合が抑制されるかを、実データをもとに検証したい。

Meta-learnerのメリット

• Meta-learner関連の手法の実務上優れた点は、「ITEとATEが一貫性のある形で容易に得られる」ことにあると思う（個人的所感）。
• ビジネスの場面では、施策全体の効果を振り返りつつ、ユーザー単位やユーザーセグメント単位での効果をもとにターゲティングを実施したい場合がある。
• IPWや回帰分析などでは、全体の効果（ATE）を推定したあとに、特定のユーザーセグメントにおける因果効果（ITEやCATE）を推定すると、各CATEの和がATEと一致しなくなり、説明が難しくなる場合がある。
• Meta-learnerでは、モデルを作成すれば、ITE, CATE, ATEが一貫性のある形で得られるので、説明がしやすい。

Meta-learnerのデメリット

• 機械学習モデルを活用することによる種々の危険性がある。
• ①正則化バイアス
  • GBDTといったモデルでは基本的に正則化を行う。
  • 正則化によって、$\sqrt{n}$ での収束性がなくなるため、バイアスが生じる。
• ②過適合
  • 一部のデータに過剰にフィットした結果になりうる。
• ③困難な解釈性
  • 交絡因子の影響がどれくらい調整できているかの確認が難しい（ここは単純な回帰ベースの場合でも同じだが）。

Meta-learner手法の比較

• 本稿では、手法の改善によってどれくらい①②を払拭できるのか（RCTの効果を得られるのか）を検討する。
• 具体的には、S-learnerを使う場合と、DDMLを使う場合とで、因果効果の推定精度がどれほど変わるかを、Lalondeデータセットをもとに検証する。
  • S-learner, DDMLを適用する場合のデータセットは、RCTの結果は得られていない状況、つまり施策非実施群のデータはCPS比較グループでしか得られていないとする。
• RCTをもとにした因果効果は以前の記事で推定済みであり、そちらを正として進める。

実装（一部抜粋）

S-learner

# X_cols: 特徴量のカラム名のlist
# t_col: 介入変数のカラム名
# y_col: 結果変数のカラム名

X_all = df_obs[X_cols + [t_col]]
y = df_obs[y_col]

kf = KFold(n_splits=n_splits, shuffle=True, random_state=42)
ite_results = np.zeros(len(df_obs))
r2_scores = []
feature_importances = []
models = []

for train_idx, val_idx in kf.split(X_all):
    X_train, X_val = X_all.iloc[train_idx], X_all.iloc[val_idx]
    y_train, y_val = y.iloc[train_idx], y.iloc[val_idx]
    
    # LightGBMモデルの定義と学習
    model = LGBMRegressor(**lgb_params)
    model.fit(X_train, y_train, 
              eval_set=[(X_val, y_val)],
              eval_metric='rmse',
              callbacks=[lgb.early_stopping(stopping_rounds=stopping_rounds)])

    # 決定係数の算出
    y_pred = model.predict(X_val)
    r2_scores.append(r2_score(y_val, y_pred))
    
    feature_importances.append(model.feature_importances_)
    
    # ITEの推定 (Validation setに対して)
    X_val_t1 = X_val.copy()
    X_val_t1[t_col] = 1
    
    X_val_t0 = X_val.copy()
    X_val_t0[t_col] = 0
    
    ite_val = model.predict(X_val_t1) - model.predict(X_val_t0)
    ite_results[val_idx] = ite_val
    models.append(model)

double/debiased machine learning

# X: 共変量, T: 処置変数(0/1), y: 結果変数
X = df_obs[X_cols]
y = df_obs[y_col]
T = df_obs[t_col]

y_res = np.zeros(len(df_obs))
t_res = np.zeros(len(df_obs))
r2_y_list = []
roc_auc_t_list = []

fi_y_list = []
fi_t_list = []

kf = KFold(n_splits=n_splits, shuffle=True, random_state=42)

for train_idx, val_idx in kf.split(X):
    X_train, X_val = X.iloc[train_idx], X.iloc[val_idx]
    y_train, y_val = y.iloc[train_idx], y.iloc[val_idx]
    T_train, T_val = T.iloc[train_idx], T.iloc[val_idx]

    # --- XからYを予測するモデルの作成 (Outcome Model) ---
    model_y = LGBMRegressor(**lgb_params)
    model_y.fit(X_train, y_train, eval_set=[(X_val, y_val)], callbacks=[lgb.early_stopping(stopping_rounds)])
    y_res[val_idx] = y_val - model_y.predict(X_val)
    r2_y_list.append(r2_score(y_val, model_y.predict(X_val)))
    fi_y_list.append(model_y.feature_importances_)

    # --- XからTを予測するモデルの作成 (Treatment Model) ---
    model_t = LGBMClassifier(class_weight='balanced', **lgb_params)
    model_t.fit(X_train, T_train, 
                eval_set=[(X_val, T_val)], 
                eval_metric='binary_logloss', # 2値分類の評価指標
                callbacks=[lgb.early_stopping(stopping_rounds), lgb.log_evaluation(period=-1)])

    # 残差の計算
    prob_t = model_t.predict_proba(X_val)[:, 1]
    t_res[val_idx] = T_val - prob_t
    roc_auc_t_list.append(roc_auc_score(T_val, prob_t))


# Yの残差をTの残差によって回帰
ddml_linear_model = LinearRegression()
ddml_linear_model.fit(t_res.reshape(-1, 1), y_res)
ate_ddml = ddml_linear_model.coef_[0]

print(f"DDML Estimated ATE: {ate_ddml:.4f}")

ddml_nonlinear_model = LGBMRegressor(random_state=42)

# 残差 T と元の特徴量 X を結合して、効果の異質性を学習
X_final = pd.concat([X, pd.Series(t_res, name='t_res', index=X.index)], axis=1)

# 学習（Yの残差を目的変数にする）
ddml_nonlinear_model.fit(X_final, y_res)

# ITEの算出: 
# 「もし処置残差(t_res)が +1 されたら y_res がどう変わるか」の微分係数に近い値を出す
X_final_t1 = X_final.copy()
X_final_t1['t_res'] = X_final['t_res'] + 0.5
X_final_t1['t_res'] = 0.5
X_final_t0 = X_final.copy()
X_final_t0['t_res'] = X_final['t_res'] - 0.5
X_final_t0['t_res'] = -0.5

ite_ddml = ddml_nonlinear_model.predict(X_final_t1) - ddml_nonlinear_model.predict(X_final_t0)

print(f"DDML (Non-linear) Estimated ATE: {np.mean(ite_ddml):.4f}")

因果効果の推定結果と解釈

ATE

• DDMLの方がRCTに近い結果となった
  • 残差回帰をすることで①②の改善がありそう

	RCT	S-learner	DDML
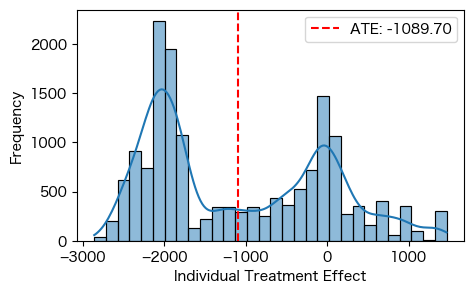
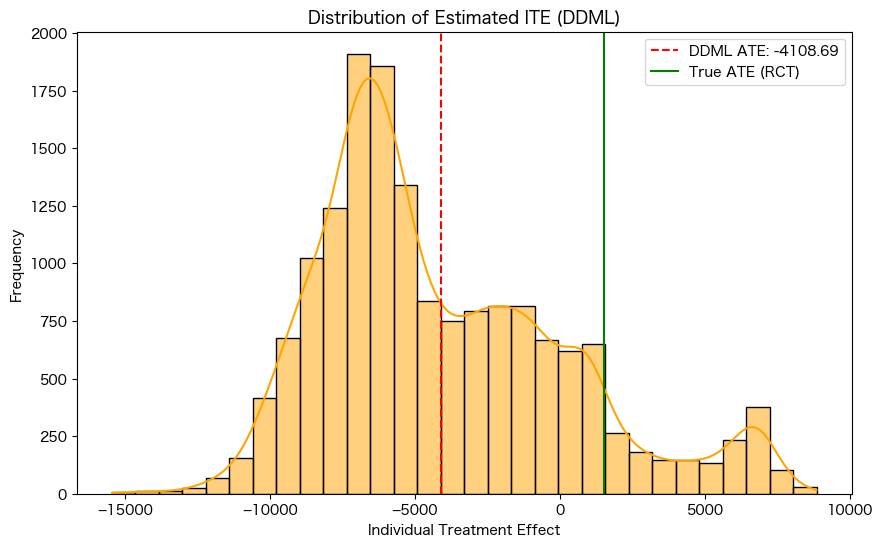
因果効果	886.30	-1089.7	308.4

ITE

• ITEについてはDDMLだと逆にRCTの結果から大きくズレる結果となった
• 理由としては下記の2つが考えられる
  • ITEを求めるために、残差回帰をLightGBMで実施しているために、過適合や正則化バイアスが発生している
  • ITEの算出方法として、Tの残差が、-0.5から0.5に1変化したときの傾きを効果として簡易的に実施しているが、この方法が適切でない

S-learnerで導出したITE

DDMLで導出したITE

まとめ

• DDMLを活用することで、正則化バイアスを減らして因果効果を推定することができた
• 実務でもできるだけDDMLを使用していくことが望ましい
• 一方で、DDMLを用いてITEを求めるには工夫が必要である
  • 今回ここは調査しきれなかったので、次回の記事で調査したい

参考文献

• 因果推論: 基礎から機械学習・時系列解析・因果探索を用いた意思決定のアプローチ(オーム社, 2024)