HOG特徴量とSVMで物体検出

概要

HOG特徴量とSVMで物体検出をやってみたいと思います。よくある例は二値画像やマークなので、自然画像で試してみたいと思います。データは前回の記事と同じものを利用します。

前回の記事

データ

今回も丸太を検出してみようと思います。データはphotoACからダウンロードしました。推論対象画像はこの画像とこの画像のSサイズを使用し、学習用画像はこの画像のMサイズから正例と負例を10枚ずつトリミングしました。

推論対象画像1

推論対象画像2

正例画像

負例画像

プログラム

下記のライブラリをインストールします。

pip install numpy
pip install matplotlib
pip install opencv-python
pip install scikit-learn

下記は物体検出を実行するコードです。

main.py

import json
from typing import Tuple

import cv2
import numpy as np
from matplotlib import pyplot as plt
from sklearn.exceptions import NotFittedError
from sklearn.svm import SVC


def plot_box(img, boxes):
    result_img = img.copy()
    for box in boxes:
        result_img = cv2.rectangle(
            result_img,
            pt1=box[:2],
            pt2=box[2:],
            color=(255, 0, 0),
            thickness=2)
    return result_img


def nms(boxes, scores, nms_thresh=0.5, top_k=200):
    """
    boxes: np.array([[x1, y1, x2, y2],...])
    """
    keep = []
    if len(boxes) == 0:
        return keep
    x1 = boxes[:, 0]
    y1 = boxes[:, 1]
    x2 = boxes[:, 2]
    y2 = boxes[:, 3]
    area = (x2 - x1) * (y2 - y1)
    idx = np.argsort(scores, axis=0)
    idx = idx[-top_k:]

    while len(idx) > 0:
        last = len(idx)-1
        i = idx[last]  # index of current largest val
        keep.append(i)
        xx1 = np.maximum(x1[i], x1[idx[:last]])
        yy1 = np.maximum(y1[i], y1[idx[:last]])
        xx2 = np.minimum(x2[i], x2[idx[:last]])
        yy2 = np.minimum(y2[i], y2[idx[:last]])

        w = np.maximum(0, xx2 - xx1)
        h = np.maximum(0, yy2 - yy1)

        inter = w * h
        union = area[idx[:last]] + area[i] - inter
        iou = np.divide(
            inter, union,
            out=np.full_like(union.astype(np.float64), np.nan),
            where=union != 0)
        idx = np.delete(idx, np.concatenate(
            ([last], np.where(iou > nms_thresh)[0])))
    return boxes[keep], scores[keep]


class SlidingWindow():
    def __init__(
        self,
        window_size: Tuple[int, int],
        step: Tuple[int, int] = (1, 1),
        padding: Tuple[int, int] = (0, 0)
    ):
        """
        window_size: (y, x)
        """
        self.window_size = window_size
        self.step = step
        self.padding = padding

    def coords(self, img_size):
        """
        Return:
            [(x1, y1, x2, y2), ...]
        """
        rows, cols = img_size
        window_size = self.window_size
        step = self.step
        padding = self.padding
        i_idxs = np.arange(
            padding[0], rows+padding[0]-window_size[0]+1, step[0])
        j_idxs = np.arange(
            padding[1], cols+padding[1]-window_size[1]+1, step[1])

        ret = []
        for i in i_idxs:
            for j in j_idxs:
                ret.append(
                    [int(j), int(i),
                     int(j+window_size[1]), int(i+window_size[0])]
                )
        return ret

    def unpadding_coord(self, img_size, coords: list):
        """
        coords: [(x1, y1, x2, y2),...]

        Return:
            [(x1, y1, x2, y2),...]
        """
        rows, cols = img_size
        padding = self.padding
        ret = []
        for i_coord in coords:
            x1, y1, x2, y2 = list(map(int, i_coord))
            x1_ = min(max(x1-padding[1], 0), cols)
            y1_ = min(max(y1-padding[0], 0), rows)
            x2_ = min(max(x2-padding[1], 0), cols)
            y2_ = min(max(y2-padding[0], 0), rows)
            area = (y2_ - y1_) * (x2_ - x1_)
            if area <= 0:
                x1_, y1_, x2_, y2_ = (-1, -1, -1, -1)
            ret.append([x1_, y1_, x2_, y2_])
        return ret


class HogDescriptor:
    def __init__(
            self,
            win_size: Tuple[int, int] = (64, 64),
            block_size: Tuple[int, int] = (16, 16),
            block_stride: Tuple[int, int] = (8, 8),
            cell_size: Tuple[int, int] = (8, 8),
            nbins: int = 9,
    ):
        self.win_size = win_size
        self.block_size = block_size
        self.block_stride = block_stride
        self.cell_size = cell_size
        self.nbins = nbins
        self._hog = cv2.HOGDescriptor(
            win_size,
            block_size,
            block_stride,
            cell_size,
            nbins
        )
        self.feature_dim = HogDescriptor.calc_feature_dim(
            win_size, block_size, block_stride, nbins)

    def get_feature_dim(self):
        return self.feature_dim

    def compute(self, imgs: list):
        if not isinstance(imgs, list):
            raise ValueError('imgs must be list of image array.')

        X = []
        for i_img in imgs:
            descriptor = self._hog.compute(i_img)
            descriptor = descriptor.ravel()
            assert descriptor.shape[0] == self.feature_dim
            X.append(descriptor)
        X = np.array(X)
        return X

    @staticmethod
    def calc_feature_dim(win_size, block_size, block_stride, nbins):
        num_cell_per_block = block_size[0] / \
            block_stride[0] * block_size[1]/block_stride[1]
        num_h_block = (win_size[0] - block_size[0]) / block_stride[0] + 1
        num_w_block = (win_size[1] - block_size[1]) / block_stride[1] + 1
        num_block = num_h_block * num_w_block
        return int(num_cell_per_block * num_block * nbins)


class HogSvmAdapter:
    def __init__(
            self,
            hog: HogDescriptor,
            clf: SVC,
            window_size: Tuple[int, int],
            scales: Tuple[float, ...] = (1.0,),
            step: Tuple[int, int] = (1, 1),
            padding: Tuple[int, int] = (0, 0),
    ):
        self.hog = hog
        self.clf = clf
        self.window_size = window_size
        self.scales = scales
        self.padding = padding
        self.step = step
        self.sw_list = [
            SlidingWindow(
                window_size=[int(s*r)for s in window_size],
                step=step,
                padding=padding) for r in scales]

        if clf.fit_status_ == 1:
            raise NotFittedError('SVC instance is not fitted yet.')

    def predict(
            self,
            img: np.ndarray,
            threshold: float = 0.01,
            nms_thresh: float = 0.1,
            top_k: int = 0):
        img_padded = np.pad(img, self.padding, mode='constant')

        # スライディングウィンドウの座標で画像をクロップしHOG特徴量を計算
        all_boxes, all_scores = [], []
        for sw in self.sw_list:
            coords = sw.coords(img_padded.shape[:2])
            cropped_img_descriptor = []
            cropped_imgs = []
            for i_coord in coords:
                x1, y1, x2, y2 = i_coord
                cropped = img_padded[y1:y2, x1:x2]
                cropped_resized = cv2.resize(cropped, (64, 64))
                cropped_imgs.append(cropped_resized)
            cropped_img_descriptor = self.hog.compute(cropped_imgs)
            # クロップした画像に対してSVMで推論
            scores = self.clf.decision_function(cropped_img_descriptor)
            # 閾値でボックスをフィルター
            unpad_coords = sw.unpadding_coord(img.shape[:2], coords)
            boxes = np.array(unpad_coords)
            boxes = boxes[scores > threshold]
            scores = scores[scores > threshold]
            all_boxes.append(boxes)
            all_scores.append(scores)
        all_boxes = np.concatenate(all_boxes, axis=0)
        all_scores = np.concatenate(all_scores, axis=0)

        # NMSを実行
        boxes_detect_nms, scores_nms = nms(
            all_boxes, all_scores, nms_thresh, top_k)
        return boxes_detect_nms, scores_nms


def main():
    # 学習画像読み込み
    imgs, labels = [], []
    for j in [0, 1]:
        for i in range(1, 11):
            img = cv2.imread(f'./train/{j}/{i:03d}.png', cv2.IMREAD_GRAYSCALE)
            img = cv2.resize(img, (64, 64))
            imgs.append(img)
            labels.append(j)

    # HOG特徴量を計算
    params = {
        'win_size': (64, 64),  # (x, y)
        'block_size': (16, 16),
        'block_stride': (8, 8),
        'cell_size': (8, 8),
        'nbins': 9
    }
    hog = HogDescriptor(**params)
    X_train = hog.compute(imgs)
    y_train = np.array(labels)

    # SVMを学習
    clf = SVC(kernel='rbf', gamma=0.001, probability=True)
    clf.fit(X_train, y_train)

    hogsvm = HogSvmAdapter(
        hog, clf,
        window_size=params['win_size'][::-1],
        scales=(1.0, 0.7, 0.8, 0.9, 1.1),
        step=(8, 8),
        padding=(32, 32)
    )

    # 推論対象画像読み込み
    filenames = [
        './22456235_s.jpg',
        './25153855_s.jpg'
    ]
    results, result_imgs = [], []
    for i, fname in enumerate(filenames):
        # 推論対象画像読み込み
        img = cv2.imread(fname)
        img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY)
        boxes, scores = hogsvm.predict(
            img_gray, threshold=-1, nms_thresh=0.1, top_k=0)

        # 検出結果を保存
        for j, (box, score) in enumerate(zip(boxes, scores)):
            detected_instance = {
                'id': j+1,
                'image_id': i+1,
                'category_id': 1,
                'iscrowd': 0,
                'segmentation': []
            }
            x1, y1, x2, y2 = list(map(int, box))
            detected_instance['bbox'] = [x1, y1, x2 - x1, y2 - y1]
            detected_instance['area'] = (x2 - x1) * (y2 - y1)
            detected_instance['score'] = float(score)
            results.append(detected_instance)

        result_img = plot_box(img, boxes)
        result_img = cv2.cvtColor(result_img, cv2.COLOR_BGR2RGB)
        result_imgs.append(result_img)

    with open('./detections_coco.json', 'w') as f:
        json.dump(results, f, indent=4)

    # Boxを表示する
    for result_img in result_imgs:
        plt.imshow(result_img)
        plt.show()


if __name__ == '__main__':
    main()

plot_box 関数は、画像に検出したボックスを描く関数です。

nms関数はNMS (Non-Maximum Suppression)を実行する関数です。スライディングウィンドウを使用して物体位置を特定するため、物体がある場所に複数のボックスを検出しやすいです。したがって、重複するボックスを排除することが必要となります。

SlidingWindowクラスはスライディングウィンドウの座標を出力するクラスです。

HogDescriptorクラスはcv2.HOGDescriptorをラップしており、画像のリストを受け取ってHOG特徴量を出力します。

HogSvmAdapterはHOG特徴量計算器とSVMの予測器のアダプターであり、画像を入力としてスライディングウィンドウを生成し、物体検出、NMSを実行します。

main関数ではSVMの学習と予測を行っています。ボックスの検出結果をCOCOフォーマットでファイルに出力しています。

検出結果

SVMの予測の確信度には分離境界面からの距離を使用しています。SVMのクラスにはメソッドpredict_probaも実装されていますが、このメソッドは分類結果と矛盾が生じる可能性があり($ \mathrm{argmax}(P(C|X))\neq C$)、使いにくいです。そこで、分離境界面からの距離を出力するdecision_functionを使用していますが、こちらの値は正規化等はされていないので、確信度の分布を見て閾値を適切に決定することが必要になります。

評価のコードは以前の記事で紹介しています。

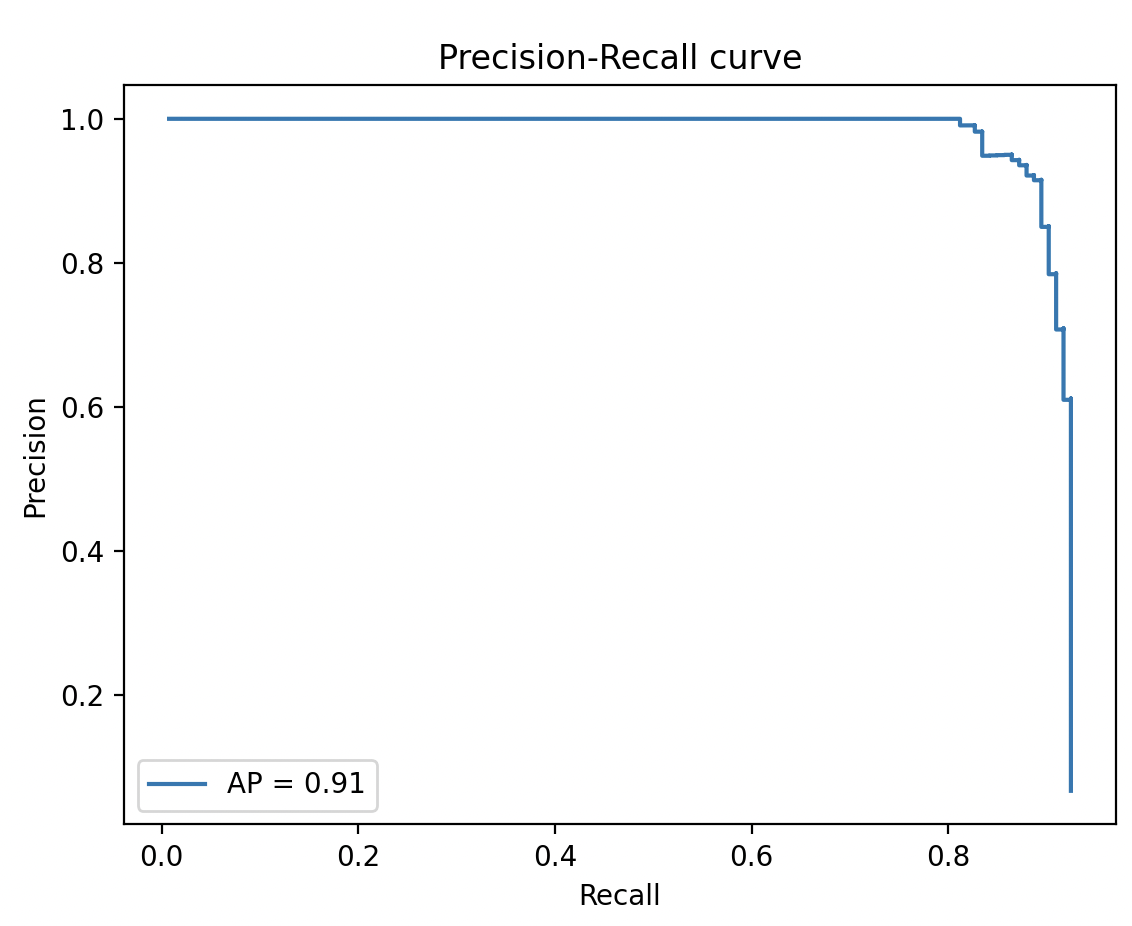
確信度の閾値を$-1$に設定し、予測を実行します。APは91.3となりました。下図はPrecision-Recall 曲線です。

AP@IoU=0.5, nms=0.1, [tex: \mathrm{maxDets}=infty]
91.3

*Precision-Recall 曲線

下記は確信度の閾値を0.01に設定したときの精度です。

	real_pos	real_neg
pred_pos	tp = 119	fp = 21
pred_neg	fn = 14	-

Precision@IoU=0.5,conf=0.01,nms=0.1	Recall@IoU=0.5,conf=0.01,nms=0.1
85.0	89.5

下図は検出結果です。

検出結果(画像1)

検出結果(画像2)

Reference