[論文]Variational Inference with Normalizing Flows

Info

• タイトル：Variational Inference with Normalizing Flows
• 著者：Danilo Jimenez Rezende, Shakir Mohamed
• 論文：https://arxiv.org/abs/1505.05770
• カンファ：PMLR2015
• プロジェクトページ：

概要

• 事後分布を近似する分布の選択は変分推論の中心的問題の一つ。
• 変分推論のほとんどの応用では、平均場または他の単純な構造の近似に焦点を当て、事後分布を単純な分布族で近似するに留まっている。
• 我々は、柔軟で任意に複雑かつスケーラブルな近似事後分布を指定するための新しいアプローチを導入する。
• 一連の可逆写像を通して確率密度を変換することにより複雑な分布を構成するツールである正規化フローを用いた近似事後分布の仕様を提案する。
• 正規化フローを用いた推論は、線形時間複雑度を持つ項を追加するだけで、より厳密な修正変分下界を提供する。
• 正規化フローが無限小のフローを認めることで、漸近領域において真の事後分布を回復できる事後近似のクラスを指定できることを示し、よく言われる変分推論の限界の一つを克服することができることを示す。
• 特殊な正規化フローを適用することで事後近似を改善する関連アプローチを統一的に示す
• 一般的な正規化フローを用いることで、他の競合する手法よりも系統的に優れた事後近似が可能であることを実験的に示す。

背景

• 近年、大規模なデータセットにおける複雑な問題に対して確率的モデリングを拡張する手段として、変分推論に大きな関心が集まっている。
• 変分法には、統計的推論のデフォルト手法としてより広く採用されることを妨げる多くの欠点がある。
• 論文で取り上げるのは、これらの制約の一つである事後近似の選択である。
  • 変分推論は、難解な事後分布を既知の確率分布のクラスで近似し、その上で真の事後分布に対する最良の近似を探索することが要求される。
  • 使用される近似のクラスは、例えば、平均場近似のように限定されることが多く、真の事後分布に類似した解は存在しないことを意味します。これは変分法に対する広く提起されている異議で、MCMCのような他の推論手法とは異なり、漸近領域においてさえ真の事後分布を回復することができない。
• また、限定的な事後近似の有害な効果を説明する多くの証拠が存在する。Turner & Sahani (2011)は、よく経験される2つの問題の解説を提供している。
  • 1つ目は、事後分布の分散の推定不足という広く観察されている問題で、選択された事後近似に基づく予測がうまくいかず、信頼性の低い決定となる可能性があるというもの。
  • もうひとつは、事後近似の容量が限られているため、任意のモデルパラメータのMAP推定値に偏りが生じることです（これは、例えば時系列モデルの場合である）。
• リッチな事後近似のための多くの提案が検討されている。
  • 典型的には，近似事後関数内に依存性の基本形を組み込んだ構造化平均場近似に基づくものである。
  • もう一つの強力な代替案は、Jaakkola & Jordan (1998); Jordan et al. (1999); Gershman et al. (2012)によって開発されたような混合モデルとして近似事後を指定することである。しかし、混合物アプローチは、パラメータ更新ごとに各混合物成分の対数尤度とその勾配を評価する必要があり、一般的に計算量が多いため、変分推論の潜在的なスケーラビリティを制限している。
• 本論文では、変分推論のための近似的な事後分布を指定するための新しいアプローチを紹介する。

手法

推論を行うには確率モデルの周辺尤度を用いて推論すればよく、モデル中の欠落変数や潜在変数の周辺化が必要である。この積分は一般的に困難であり、その代わりに周辺尤度の下界を最適化する。観測値x、積分すべき潜在変数z、モデル・パラメータθを持つ一般的な確率モデルを考える。潜在変数qφ (z|x) の近似事後分布を導入し、変分原理 (Jordan et al., 1999) に従って、周辺尤度の境界を得る

変分推論

変分推論と言っているが、実態としてはEMアルゴリズムである。比較的複雑な分布$p(\boldsymbol{x})$に対して潜在変数$\boldsymbol{z}$を導入して、より扱いやすい形の同時分布$p(\boldsymbol{x}, \boldsymbol{z} )$を考えることが出来る場合がある。同時分布$p(\boldsymbol{x}, \boldsymbol{z} )$を求めた後、周辺化を行うことで$p(\boldsymbol{x})$を求める事ができる。教科書的な例では混合ガウス分布がある。

ある観測変数$\boldsymbol{x}$が従う分布を求めたい。分布をモデリングしたものを$p_\theta(\boldsymbol{x})\equiv p(\boldsymbol{x}\mid \theta)$と書くことにする。$\theta$はモデルパラメーターである。

複雑な分布をいきなりモデリングすることは難しい。そこで、潜在変数$\boldsymbol{z}$を導入してモデリングが単純になることを期待する。

\begin{align}
p_\theta(\boldsymbol{x}) = \int p_\theta(\boldsymbol{x}\mid \boldsymbol{z})p_\theta(\boldsymbol{z}) dz.
\end{align}

この$p_\theta(\boldsymbol{z})\equiv p(\boldsymbol{z}\mid \theta)$の分布は一般に不明であるため、変分推論で近似する。近似分布は$q_\phi(\boldsymbol{z}\mid \boldsymbol{x})$でモデリングする。$\phi$はモデルのパラメーターである。

\begin{align}
p_\theta(\boldsymbol{x}) = \int p_\theta(\boldsymbol{x}\mid \boldsymbol{z})p_\theta(\boldsymbol{z}) \frac{q_\phi(\boldsymbol{z}\mid \boldsymbol{x})}{q_\phi(\boldsymbol{z}\mid \boldsymbol{x})}dz.
\end{align}

対数尤度を計算する。

\begin{align}
\log p_\theta(\boldsymbol{x}) 
&= \log\int p_\theta(\boldsymbol{x}\mid \boldsymbol{z})p_\theta(\boldsymbol{z}) \frac{q_\phi(\boldsymbol{z}\mid \boldsymbol{x})}{q_\phi(\boldsymbol{z}\mid \boldsymbol{x})}dz \\
&\geq \int \log \left[p_\theta(\boldsymbol{x}\mid \boldsymbol{z})p_\theta(\boldsymbol{z}) \frac{1}{q_\phi(\boldsymbol{z}\mid \boldsymbol{x})} \right] q_\phi(\boldsymbol{z}\mid \boldsymbol{x}) dz \\
&= -\mathrm{D_{KL}}(q_\phi(\boldsymbol{z}\mid \boldsymbol{x}) \| p_\theta(\boldsymbol{z})) + E_{q_\phi}[\log p_\theta(\boldsymbol{x}\mid \boldsymbol{z})] \\
& \equiv - \mathcal F(\boldsymbol{x}).
\end{align}

1行目から2行目への変形はイェンセンの不等式を使用した。$- \mathcal F(\boldsymbol{x})$を変分下限（Evidence lower bound; ELBO）または自由エネルギー（の負符号）と呼ぶ。第一項は潜在変数の分布とそれをモデリングした分布のKLダイバージェンスで、これらの分布が一致するとき最大化される。第二項はデータの分布のモデリングに対する尤度で、$p_\theta(\boldsymbol{x}\mid \boldsymbol{z})$がデータの分布をよく再現できているほど大きくなる。

$\log p_\theta(\boldsymbol{x})$は計算できないので、代わりにその下限である$- \mathcal F(\boldsymbol{x})$の最大化問題を考えることで、尤度最大化問題の代わりとする。パラメーターは、データ分布のモデリングのパラメーター$\theta$と、変分推論のパラメーター$\phi$を最適化することになる。本論文では変分推論のパラメーター$\phi$の最適化のみ考える。

最適化のベストプラクティスは、ミニバッチと確率的勾配降下を用いてこの最適化を行うものである。これによって変分推論を非常に大きなデータセットを持つ問題にスケールアップすることができる。しかし、変分推論がうまくいくために解決すべき二つの問題がある。

• 期待対数尤度$\nabla\phi E_{q_\phi(\boldsymbol{z})} [\log p_\theta(\boldsymbol{x}\mid \boldsymbol{z})]$の導関数を効率的に計算すること。
• 様々な分布を表現できる豊かさがあり、かつ計算可能な近似事後分布$q$を選択すること。

本論文の焦点は2番目の問題である。最初の問題に対処するために、我々は2つのツールを利用する。モンテカルロ勾配推定と推論ネットワークであり、これらを併用することでamortized variational inferenceと呼ばれる。

勾配計算はモンテカルロ近似と組み合わせた期待値の非中心再パラメータ化（Papaspiliopoulosら, 2003; Williams, 1992）を使用して、必要な勾配を計算する。

近似事後分布$q$には認識モデルやInference Networkを使用する。Inference Networkは、観測値から潜在変数への逆写像を学習するモデルである。最も単純な推論モデルは対角ガウス分布$q_\phi(\boldsymbol{z}\mid \boldsymbol{x})=\mathcal N(\boldsymbol{z}\mid \boldsymbol{\mu}_\phi(\boldsymbol{x}), \mathrm{diag}(\sigma^2_{\phi}(\boldsymbol{x})))$であり、平均関数$\boldsymbol{\mu}_\phi(\boldsymbol{x})$と標準偏差関数 $\sigma^2_{\phi}(\boldsymbol{x})$は深いニューラルネットワークの出力である。

深層潜在ガウスモデル（DLGM）

本論文では深層有向グラフモデルの一般クラスである深層潜在ガウスモデル（DLGM）を研究する。DLGMは、層$l$に対するガウス潜在変数$\boldsymbol{z}_l$の$L$層の階層構造からなり、各潜在変数の層は上の層に非線形に依存し、DLGMでは、この非線形依存関係は深層ニューラルネットワークで規定される。

\begin{align}
p(\boldsymbol{x}, \boldsymbol{z}_1, \cdots, \boldsymbol{z}_L)
= p(\boldsymbol{x} \mid f_0(\boldsymbol{z}_1))\prod_{l=1}^L p(\boldsymbol{z}_l \mid f_l(\boldsymbol{z}_{l+1})).
\end{align}

各潜在変数の事前分布は標準正規分布$p(\boldsymbol{z}_l)=\mathcal N(\boldsymbol{0}, I)$とする。
結合確率モデル$p(\boldsymbol{x} \mid f_0(\boldsymbol{z}_1))$は$\boldsymbol{z}_1$を条件とし、ディープニューラルネットワークによってパラメータ化される。このモデルクラスは非常に一般的であり、因子分析やPCA、非線形因子分析、非線形ガウス信念ネットワークなどの他のモデルを特殊なケースとして含んでいる。

Normalizing Flows

正規化フローは、一連の可逆写像を通した確率密度の変換を記述するものである。変数の変化のルールを繰り返し適用することで、最初の密度が一連の可逆写像の中を「流れる」。この一連の流れが終わると、有効な確率分布が得られるので、このような流れを正規化フローと呼ぶ。

Finite Flows

密度の変換の基本ルールは、可逆的で滑らかな写像$f:\mathbb{R}^d \rightarrow \mathbb{R}^d,g=f^{-1}$を考える。すなわち、合成は$g\circ f(\boldsymbol{z}) =\boldsymbol{z}$となる。この写像を用いて分布$q(\boldsymbol{z})$を持つ確率変数$\boldsymbol{z}$を変換すると、得られる確率変数$\boldsymbol{z}'=f(\boldsymbol{z})$の分布は 、

\begin{align}
q(\boldsymbol{z}') 
&= q(\boldsymbol{z})\left| \det \frac{\partial f^{-1}}{\partial \boldsymbol{z}'} \right|\\
&= q(\boldsymbol{z})\left| \det \frac{\partial f}{\partial \boldsymbol{z}} \right|,
\end{align}

となる。いくつかの簡単な写像を合成し、この変換を順次適用することにより、任意に複雑な確率密度を構成することができる。分布$q_0$の確率変数$\boldsymbol{z}_0$を$K$個の変換$f_k$の連鎖によって連続的に変換して得られる密度$q_K(\boldsymbol{z})$は、

\begin{align}
\boldsymbol{z}_K &= f_K \circ \cdots \circ f_{2}\circ f_{1}(\boldsymbol{z}_0) \\
\log q_K(\boldsymbol{z}_K) 
 & = \log q_0(\boldsymbol{z}_0) - \sum_{k=1}^K \log \left| \det \frac{\partial f_k}{\partial \boldsymbol{z}_{k-1}} \right|,
\end{align}

となる。

初期分布$q_0(\boldsymbol{z}_0)$を持つ確率変数$\boldsymbol{z}_k = f_k(\boldsymbol{z}_{k-1})$ が通る経路をフローと呼び、連続する分布$q_k$ が形成する経路を正規化フローという。このような変換の特性は、しばしば無意識の統計学者の法則（law of the unconscious statisticia; LOTUS）と呼ばれ、変換された密度$q_K$ に対する期待値が$q_K$ を明示的に知ることなく計算できる。

\begin{align}
E_{q_K}[h(\boldsymbol{z}_K)] = E_{q_0}[h(f_K \circ \cdots \circ f_{2}\circ f_{1}(\boldsymbol{z}_0))].
\end{align}

つまり、$h(\boldsymbol{z})$ が $q_K$ に依存しない場合、logdet Jacobian 項の計算を必要としない。

可逆フローの効果は、初期密度に対する膨張または収縮のシーケンスとして理解することができる。膨張の場合、写像$\boldsymbol{z}'=f(\boldsymbol{z})$は点$\boldsymbol{z}$を$\mathbb{R}^d$のある領域から引き離し、その領域の密度を下げ、その領域の外側の密度を上げることになる。逆に、収縮の場合、写像は点を領域の内部に押しやり、その内部の密度を増加させ、外部の密度を減少させる。

正規化フローの形式は、変分推論に必要な近似的な事後分布$q(\boldsymbol{z}|\boldsymbol{x})$を指定する体系的な方法を与えてくれるようになった。変換$f_K$の適切な選択により、最初は独立ガウス分布のような単純な因数分解分布を用い、異なる長さの正規化フローを適用して、次第に複雑で多峰性のある分布を得ることができる。

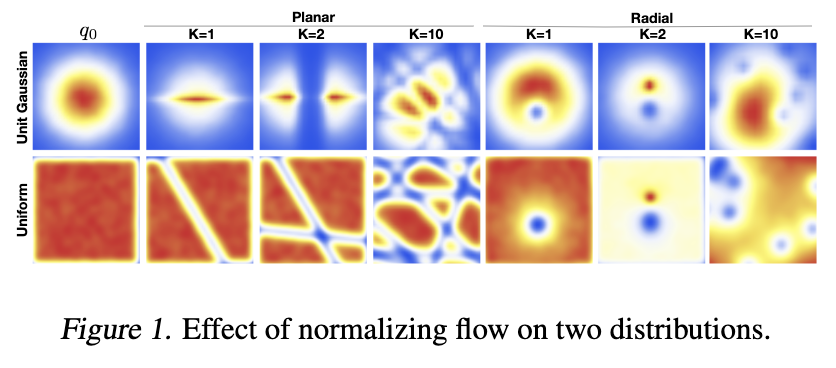
Inference with Normalizing Flows

有限正規化フローを用いたスケーラブルな推論を可能にするためには、使用可能な可逆変換のクラスと、ヤコビアンの行列式を計算するための効率的なメカニズムを指定する必要がある。可逆パラメトリック関数、例えば、可逆ニューラルネットワーク（Bairdら、2005；Rippel＆Adams、2013）を構築することは簡単であるが、そのようなアプローチは、一般に、$D$が隠れ層の次元、$L$が使用する隠れ層の数で、$O(LD^3)$としてスケールするヤコビアン行列式を計算する複雑さを有する。さらに、ヤコビアン行列式の勾配を計算するためには、$O(LD^3)$であり、数値的に不安定な行列逆行列を含むいくつかの追加演算が必要である。そこで、行列式を低コストで計算できる、あるいはヤコビアンを全く必要としない正規化フローが必要となる。

本論文では次の変換を考える。

\begin{align}
f(\boldsymbol{z}) = \boldsymbol{z} + \boldsymbol{u}h(\boldsymbol{w}^\top \boldsymbol{z}+b).
\end{align}

ここで$\boldsymbol{w}\in \mathbb{R}^D,\boldsymbol{u}\in \mathbb{R}^D,b\in \mathbb{R}$はパラメーターで、$h$は成分ごとの非線形変換関数である。この変換では logdetの計算量は$O(D)$となる。

\begin{align}
\boldsymbol{\psi}(\boldsymbol{z}) &= h'(\boldsymbol{w}^\top \boldsymbol{z}+b)\boldsymbol{w},\\
\left| \det \frac{\partial f}{\partial \boldsymbol{z}} \right| 
&= \left| \det(I+\boldsymbol{u}\boldsymbol{\psi}(\boldsymbol{z})^\top) \right| \\
&= \left| 1+\boldsymbol{u}^\top\boldsymbol{\psi}(\boldsymbol{z})\right|.
\end{align}

これを代入して次を得る。

\begin{align}
\boldsymbol{z}_K &= f_K \circ \cdots \circ f_{2}\circ f_{1}(\boldsymbol{z}_0) \\
\log q_K(\boldsymbol{z}_K) 
 & = \log q_0(\boldsymbol{z}_0) - \sum_{k=1}^K \log \left| 1+\boldsymbol{u}_k^\top\boldsymbol{\psi}_k(\boldsymbol{z}_{k-1})\right|.
\end{align}

このフローは、超平面$\boldsymbol{w}^\top \boldsymbol{z}+b=0$に垂直な方向に一連の収縮と膨張を適用して初期密度q0を変更するので、これらのマップを平面フローと呼ぶことにする。

この変換関数は全ての定義域で逆変換が存在するわけではないが、逆変換が存在するような領域にとどまるように数値計算を工夫する。

Flow-Based Free Energy Bound

近似事後分布を$q_\phi(\boldsymbol{z}\mid \boldsymbol{x})=q_K(\boldsymbol{z}_K)$とする。自由エネルギーの式を変形すると次のようになる。

\begin{align}
\mathcal F(\boldsymbol{x})
&= \mathrm{D_{KL}}(q_\phi(\boldsymbol{z}\mid \boldsymbol{x}) \| p_\theta(\boldsymbol{z})) - E_{q_\phi}[\log p_\theta(\boldsymbol{x}\mid \boldsymbol{z})] \\
&= -\int \log \left[p_\theta(\boldsymbol{x}\mid \boldsymbol{z})p_\theta(\boldsymbol{z}) \frac{1}{q_\phi(\boldsymbol{z}\mid \boldsymbol{x})} \right] q_\phi(\boldsymbol{z}\mid \boldsymbol{x}) dz \\
&= E_{q_\phi(\boldsymbol{z}\mid \boldsymbol{x})}\left[\log q_\phi(\boldsymbol{z}\mid \boldsymbol{x}) - \log p_\theta(\boldsymbol{x}, \boldsymbol{z})\right] \\
&= E_{q_0(\boldsymbol{z}_0)}\left[\log q_K(\boldsymbol{z}_K) - \log p_\theta(\boldsymbol{x}, \boldsymbol{z}_K)\right] \\
&= E_{q_0(\boldsymbol{z}_0)}\left[\log q_0(\boldsymbol{z}_0)\right]  - E_{q_0(\boldsymbol{z}_0)}\left[ \sum_{k=1}^K \log \left| 1+\boldsymbol{u}_k^\top\boldsymbol{\psi}_k(\boldsymbol{z}_{k-1})\right| \right]
-E_{q_0(\boldsymbol{z}_0)}\left[\log p_\theta(\boldsymbol{x}, \boldsymbol{z}_K)\right]
\end{align}

第一項は$q_0$に関するエントロピー、第二項は変数変換に関する補正項とみなせる。第三項は潜在変数まで含めたモデルの尤度である。このフォーマリズムは、一般化変分EMを含むあらゆる変分最適化スキームで使用することができる。

本論文の変分推論では、ディープニューラルネットワークを用いて推論モデルを構築し、観測値$\boldsymbol{x}$から初期密度$q_0 = \mathcal N (\boldsymbol{\mu}, \boldsymbol{\sigma}) ,(\boldsymbol{\mu}\in \mathbb{R}^D, \boldsymbol{\sigma} \in \mathbb R^D )$のパラメーター、およびフローのパラメーターへのマッピングを構築する。自由エネルギーの第三項は再構成誤差と解釈する(※コメント：本論文では$p_\theta$にDLGMを用いているらしいが、尤度の計算をただの再構成誤差にしているっぽい？それでいいんだっけ？)。

抽象的なネットワーク図は次のようになる。

アルゴリズムは下図のようにまとめられる。

• まず、データ$\mathcal D$からミニバッチ$\boldsymbol{x}$を取り出す。
• エンコーダーを使用してミニバッチを潜在空間へマッピングする。このとき、マッピング先の$\boldsymbol{z}_0$は単純な分布（正規分布や一様分布）に従う。
• 変数変換を行い、$\boldsymbol{z}_0$を$\boldsymbol{z}_K$に変換する。この$\boldsymbol{z}_K$は比較的複雑な分布に従う。
• ミニバッチ$\boldsymbol{x}$と$\boldsymbol{z}_K$を$\mathcal F(\boldsymbol{x}, \boldsymbol{z}_K)$に入力する。つまり、再構成誤差と$\boldsymbol{z}_K$の対数尤度を計算し、それらを組み合わせて損失関数を計算する。
• 得られた損失をもとに勾配法でパラメーターを更新する。

以上がアルゴリズムである。

評価

潜在変数のFlowの部分だけの再構成結果。

Flowの層を増やす事による効果。

他のモデルとの尤度の比較。

まとめ・感想

• Normalizing Flows では潜在変数の分布に比較的複雑な分布を用いれるように変分推論を構築。
• 本手法は事後分布の変分推論のあらゆるスキームで使用可能。

おまけ

VAEとの比較

VAEでは自由エネルギーの式をそのまま使用していた。

\begin{align}
\log p_\theta(\boldsymbol{x}) 
&= \log\int p_\theta(\boldsymbol{x}\mid \boldsymbol{z})p_\theta(\boldsymbol{z}) \frac{q_\phi(\boldsymbol{z}\mid \boldsymbol{x})}{q_\phi(\boldsymbol{z}\mid \boldsymbol{x})}dz \\
&\geq \int \log \left[p_\theta(\boldsymbol{x}\mid \boldsymbol{z})p_\theta(\boldsymbol{z}) \frac{1}{q_\phi(\boldsymbol{z}\mid \boldsymbol{x})} \right] q_\phi(\boldsymbol{z}\mid \boldsymbol{x}) dz \\
&= -\mathrm{D_{KL}}(q_\phi(\boldsymbol{z}\mid \boldsymbol{x}) \| p_\theta(\boldsymbol{z})) + E_{q_\phi}[\log p_\theta(\boldsymbol{x}\mid \boldsymbol{z})] \\
& \equiv - \mathcal F(\boldsymbol{x}).
\end{align}

$p_\theta(\boldsymbol{x}\mid \boldsymbol{z})$がデコーダー(生成器)に相当し、潜在空間の点をデータの空間の点にマップする。$q_\phi(\boldsymbol{z}\mid \boldsymbol{x})$が潜在変数の分布を近似する関数近似器であり、エンコーダー(特徴抽出器)に相当する。

$p_\theta(\boldsymbol{z})$は任意の分布に設定可能で、VAEでは正規分布（もしくはベルヌーイ分布）にすることが多いような気がします。つまり、Normalizing Flowsとは異なり、真の複雑な分布を求めるのではなく、エイヤで単純な分布を置いてしまっているわけです。

Diffusion Modelsへの橋渡し

NICE¹やReal NVP²では、潜在変数の分布を近似するのではなく、データの分布を近似して生成モデル化している。

\begin{align}
\boldsymbol{z} &= f^{-1}(\boldsymbol{x}) \\
\log p(\boldsymbol{x}) 
 & = \log q(\boldsymbol{z}) - \log \left| \det \frac{\partial f}{\partial \boldsymbol{z}} \right|,
\end{align}

抽象的なネットワーク図は次のようになる。

これが画像生成モデルとして使用される。NICEによる生成例を下記に示す。

Diffusion Modelsとの比較

Diffusion Modelsの尤度の式を振り返ってみよう（参考）。

\begin{aligned}
E_{q(\boldsymbol x_0)}\left[-\log p_\theta(\boldsymbol x_0)\right]
&= E_{q(\boldsymbol x_0)}\left[ -\log\int p_\theta (\boldsymbol{x}_{0:T}) d\boldsymbol{x}_{1:T} \right]\\
&= E_{q(\boldsymbol x_0)}\left[ -\log\int q(\boldsymbol{x}_{1:T} \mid \boldsymbol{x}_0)\frac{p_\theta (\boldsymbol{x}_{0:T})}{q(\boldsymbol{x}_{1:T} \mid \boldsymbol{x}_0)} d\boldsymbol{x}_{1:T} \right]\\
&\leq E_{q(\boldsymbol x_0)}\left[ -\int q(\boldsymbol{x}_{1:T} \mid \boldsymbol{x}_0)\log\frac{p_\theta (\boldsymbol{x}_{0:T})}{q(\boldsymbol{x}_{1:T} \mid \boldsymbol{x}_0)} d\boldsymbol{x}_{1:T} \right]\\
&= E_{q(\boldsymbol x_{0:T})}\left[ -\log\frac{p_\theta (\boldsymbol{x}_{0:T})}{q(\boldsymbol{x}_{1:T} \mid \boldsymbol{x}_0)}  \right]\\
&= E_{q(\boldsymbol x_{0:T})}\left[ -\log\frac{p(\boldsymbol{x}_T) \prod_{t=1}^T p_\theta(\boldsymbol{x}_{t-1}|\boldsymbol{x}_{t})}{\prod_{t=1}^T q(\boldsymbol{x}_{t}|\boldsymbol{x}_{t-1})}  \right]\\
&= E_{q(\boldsymbol x_{0:T})}\left[ -\log p(\boldsymbol{x}_T) - \sum_{t=1}^T\log\frac{p_\theta(\boldsymbol{x}_{t-1}|\boldsymbol{x}_{t})}{q(\boldsymbol{x}_{t}|\boldsymbol{x}_{t-1})} \right]\\
&=:L
\end{aligned}

お気づきだろうか、潜在変数がないことに！！

Normalizing Flowsでは複雑な分布を変分推論で近似することを試み、潜在空間の複雑な分布を高精度で近似することに成功した。さらに近似をデータの分布に広げた生成モデルを構築した。
Diffusion Modelsではさらに、変数変換なんぞいらん！ノイズを加えて分布を破壊すればいい、そして少しづつ壊す過程は準静的断熱過程のように可逆である！という考えを取り込んだ。物理現象からヒントを得た、着眼点が素晴らしいモデルだと思う。

1. Laurent Dinh, David Krueger, Yoshua Bengio, "NICE: Non-linear Independent Components Estimation", https://arxiv.org/abs/1410.8516 ↩

2. Laurent Dinh, Jascha Sohl-Dickstein, Samy Bengio, "ensity estimation using Real NVP", https://arxiv.org/abs/1605.08803 ↩