[論文]Denoising Diffusion Probabilistic Models

Info

• タイトル：Denoising Diffusion Probabilistic Models
• カンファ：NeurIPS2020
• 著者：Jonathan Ho, Ajay Jain, Pieter Abbeel
• 論文：https://arxiv.org/abs/2006.11239
• プロジェクトページ：https://github.com/hojonathanho/diffusion

概要

• 拡散確率モデルを用いた高品質な画像合成手法を提案。
• 拡散確率モデルとランジュバンダイナミクスによるノイズ除去のスコアマッチングとの間の新しい接続に従って設計された重み付き変分バウンドによって学習される。
• unconditional CIFAR10 datasetにおいて、Inceptionスコア9.46、FIDスコア3.17を得た。256x256 LSUNでは、ProgressiveGANと同程度の標本品質を得ることができた。

背景

• 近年、様々な種類の深層生成モデルが、様々なデータモダリティにおいて高品質なサンプルを生成している。この論文では拡散確率モデル（diffusion model）の進展を紹介する。
• diffusion model は parameterized Markov chain であり、有限時間でサンプルを生成するように変分推論によって学習する。このchainの推移は、データに徐々にノイズを加えるマルコフ連鎖である拡散過程を逆に学習させるものである。拡散が微小なガウスノイズからなる場合、サンプリングチェーンの遷移も条件付きガウスに設定すればよい。
• 拡散モデルは定義が簡単で訓練も効率的であるが、高品質なサンプルを生成できることを証明したものはない。 本論文では、拡散モデルが実際に高品質なサンプルを生成できることを示し、時には他の種類の生成モデルに関する発表結果よりも優れていることを示す。
• 拡散モデルのサンプリング手順は、自己回帰モデルで通常可能であるものを大幅に一般化するビットタリングに沿って自己回帰復号に似ているプログレッシブ復号の一種であることを示す。

その標本品質にもかかわらず、我々のモデルは他の尤度ベースモデルと比較して対数尤度が優れていない（しかし、我々のモデルはエネルギーベースモデルとスコアマッチングにおいて大きな推定値の重要度サンプリングが生成することが報告されている［11，55］よりも良い対数尤度を有する）。 我々は、我々のモデルのロスレスコード長の大部分は、知覚できない画像の詳細を記述するために消費されていることを発見した（セクション4.3）。 我々は、非可逆圧縮の言語でこの現象のより洗練された分析を提示し、拡散モデルのサンプリング手順は、自己回帰モデルで通常可能であるものを大幅に一般化するビットタリングに沿って自己回帰復号に似ているプログレッシブ復号の一種であることを示す。

手法

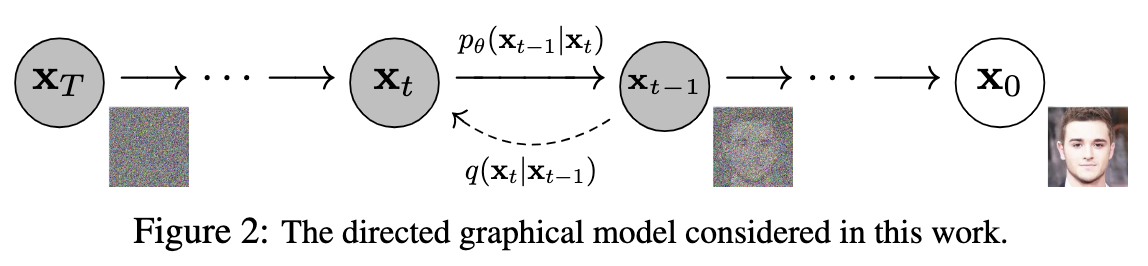
diffusion model は潜在変数を持つモデルで、生成されるサンプルの分布、

\begin{aligned}
p_\theta (\boldsymbol{x}_{0}) = \int p_\theta (\boldsymbol{x}_{0:T}) d\boldsymbol{x}_{1:T}
\end{aligned}

を学習する。学習データの分布は$\boldsymbol{x}_0 \sim q(\boldsymbol{x}_0)$である。$\boldsymbol{x}_1,...,\boldsymbol{x}_T$は$\boldsymbol{x}_0$と同じ次元を持つ変数である。$\theta$はモデルのパラメータで、ニューラルネットワークの重みとバイアスを表す。

拡散過程のリバース・プロセスはマルコフ連鎖として定義される。同時分布は次のように表される。

\begin{aligned}
p_\theta (\boldsymbol{x}_{0:T}) 
&:= p(\boldsymbol{x}_T) \prod_{t=1}^T p_\theta(\boldsymbol{x}_{t-1}|\boldsymbol{x}_{t}), \\
p_\theta(\boldsymbol{x}_{t-1}|\boldsymbol{x}_{t}) &:= \mathcal N(\boldsymbol{x}_{t-1}; \boldsymbol{\mu}_\theta(\boldsymbol{x}_t, t), \Sigma_\theta(\boldsymbol{x}_{t}, t)), \\
p(\boldsymbol{x}_T) &:= \mathcal N(\boldsymbol{x}_{T}; \boldsymbol{0}, I).
\end{aligned}

diffusion modelと他の拡散過程の違いは、フォワード・プロセスを微小なガウスノイズを加える操作として近似するところである。

\begin{aligned}
q(\boldsymbol{x}_{1:T}|\boldsymbol{x}_{0}) &= \prod_{t=1}^T q(\boldsymbol{x}_{t}|\boldsymbol{x}_{t-1}), \\
q(\boldsymbol{x}_{t}|\boldsymbol{x}_{t-1}) &:= \mathcal N(\boldsymbol{x}_{t}; \sqrt{1-\beta_t}\boldsymbol{x}_{t-1} , \beta_t I).
\end{aligned}

$\beta_t(t=1,\cdots,T)$は分散を変化させるパラメータである。

学習は$\boldsymbol x_{0}$に対して$p_\theta$の負の対数尤度が最小になるように$\theta$を決定する。負の対数尤度は直接計算できないので、変分上限を使用する。

\begin{aligned}
E_{q(\boldsymbol x_0)}\left[-\log p_\theta(\boldsymbol x_0)\right]
&= E_{q(\boldsymbol x_0)}\left[ -\log\int p_\theta (\boldsymbol{x}_{0:T}) d\boldsymbol{x}_{1:T} \right]\\
&= E_{q(\boldsymbol x_0)}\left[ -\log\int q(\boldsymbol{x}_{1:T} \mid \boldsymbol{x}_0)\frac{p_\theta (\boldsymbol{x}_{0:T})}{q(\boldsymbol{x}_{1:T} \mid \boldsymbol{x}_0)} d\boldsymbol{x}_{1:T} \right]\\
&\leq E_{q(\boldsymbol x_0)}\left[ -\int q(\boldsymbol{x}_{1:T} \mid \boldsymbol{x}_0)\log\frac{p_\theta (\boldsymbol{x}_{0:T})}{q(\boldsymbol{x}_{1:T} \mid \boldsymbol{x}_0)} d\boldsymbol{x}_{1:T} \right]\\
&= E_{q(\boldsymbol x_{0:T})}\left[ -\log\frac{p_\theta (\boldsymbol{x}_{0:T})}{q(\boldsymbol{x}_{1:T} \mid \boldsymbol{x}_0)}  \right]\\
&= E_{q(\boldsymbol x_{0:T})}\left[ -\log\frac{p(\boldsymbol{x}_T) \prod_{t=1}^T p_\theta(\boldsymbol{x}_{t-1}|\boldsymbol{x}_{t})}{\prod_{t=1}^T q(\boldsymbol{x}_{t}|\boldsymbol{x}_{t-1})}  \right]\\
&= E_{q(\boldsymbol x_{0:T})}\left[ -\log p(\boldsymbol{x}_T) - \sum_{t=1}^T\log\frac{p_\theta(\boldsymbol{x}_{t-1}|\boldsymbol{x}_{t})}{q(\boldsymbol{x}_{t}|\boldsymbol{x}_{t-1})} \right]\\
&=:L
\end{aligned}

2行目から3行目の変形はイェンセンの不等式を使用する。この$L$を勾配降下法で最小化する。

$\beta\ll 1$のとき、リバース・プロセスもガウス分布の過程になることが知られている¹。したがってニューラルネットワークは$\boldsymbol \mu_\theta$と$\boldsymbol \Sigma_\theta$を学習することになる。

フォワード・プロセスは確率変数の漸化式で表せる。

\begin{aligned}
\boldsymbol{x}_{t} &= \sqrt{1-\beta_t}\boldsymbol{x}_{t-1} + \sqrt{\beta_t}\boldsymbol\varepsilon_t \\
\boldsymbol\varepsilon_t &\sim \mathrm{W.N.}(1)
\end{aligned}

$\boldsymbol x_{t-1}$で条件付けると、期待値と分散が再現される。

\begin{aligned}
E[\boldsymbol{x}_{t}\mid \boldsymbol{x}_{t-1}] &= \sqrt{1-\beta_t}\boldsymbol{x}_{t-1}\\
V[\boldsymbol{x}_{t}\mid \boldsymbol{x}_{t-1}] &= \beta_t
\end{aligned}

漸化式を展開する。

\begin{aligned}
\boldsymbol{x}_{t} 
&= \sqrt{1-\beta_t}\boldsymbol{x}_{t-1} + \sqrt{\beta_t}\boldsymbol\varepsilon_t \\
&= \sqrt{(1-\beta_t)(1-\beta_{t-1})}\boldsymbol{x}_{t-2} + \sqrt{(1-\beta_t)\beta_{t-1}}\boldsymbol\varepsilon_{t-1}+ \sqrt{\beta_t}\boldsymbol\varepsilon_t \\
&= \sqrt{(1-\beta_t)(1-\beta_{t-1})}\boldsymbol{x}_{t-2} + \sqrt{1-(1-\beta_t)(1-\beta_{t-1})}\boldsymbol\varepsilon_{t-1}^{(1)}\\
& \quad ...\\
&= \sqrt{\prod_{s=1}^t (1-\beta_s)}\boldsymbol{x}_{0} + \sqrt{1-\prod_{s=1}^t(1-\beta_s)}\boldsymbol\varepsilon_{1}^{(t-1)}\\
&= \sqrt{\bar \alpha_t}\boldsymbol{x}_{0} + \sqrt{1-\bar\alpha_t}\boldsymbol\varepsilon_{1}^{(t-1)} \\
\end{aligned}

ここで、$\alpha_s:=1-\beta_s, \bar\alpha_t:=\prod_{s=1}^t \alpha_s$とした。また、ノイズ項は一つのノイズ項$\boldsymbol\varepsilon_{t}^{(i)}\sim \mathrm{W.N.}(I)$でまとめた。以上より次の式が得られる。

\begin{aligned}
q(\boldsymbol{x}_{t}\mid \boldsymbol{x}_{0}) = \mathcal N(\boldsymbol{x}_{t};\sqrt{\bar \alpha_t}\boldsymbol{x}_{0}, (1-\bar\alpha_t)I )
\end{aligned}

目的関数$L$について詳細を見てみる。

\begin{aligned}
L&=E_{q(\boldsymbol x_{0:T})}\left[ -\log p(\boldsymbol{x}_T) - \sum_{t=1}^T\log\frac{p_\theta(\boldsymbol{x}_{t-1}|\boldsymbol{x}_{t})}{q(\boldsymbol{x}_{t}|\boldsymbol{x}_{t-1})} \right]\\
&= E_{q(\boldsymbol x_{0:T})}\left[ -\log p(\boldsymbol{x}_T) - \sum_{t=2}^T\log\frac{p_\theta(\boldsymbol{x}_{t-1}|\boldsymbol{x}_{t})}{q(\boldsymbol{x}_{t}|\boldsymbol{x}_{t-1})}-\log\frac{p_\theta(\boldsymbol{x}_{0}|\boldsymbol{x}_{1})}{q(\boldsymbol{x}_{1}|\boldsymbol{x}_{0})} \right] \\
&= E_{q(\boldsymbol x_{0:T})}\left[ -\log p(\boldsymbol{x}_T) - \sum_{t=2}^T\log\frac{p_\theta(\boldsymbol{x}_{t-1}|\boldsymbol{x}_{t})}{q(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_{t},\boldsymbol{x}_{0})}\cdot \frac{q(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_{0})}{q(\boldsymbol{x}_{t}\mid\boldsymbol{x}_{0})} -\log\frac{p_\theta(\boldsymbol{x}_{0}|\boldsymbol{x}_{1})}{q(\boldsymbol{x}_{1}|\boldsymbol{x}_{0})} \right] \\
&= E_{q(\boldsymbol x_{0:T})}\left[ -\log p(\boldsymbol{x}_T) - \sum_{t=2}^T\log\frac{p_\theta(\boldsymbol{x}_{t-1}|\boldsymbol{x}_{t})}{q(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_{t},\boldsymbol{x}_{0})}-\log \frac{q(\boldsymbol{x}_{1}\mid\boldsymbol{x}_{0})}{q(\boldsymbol{x}_{T}\mid\boldsymbol{x}_{0})} -\log\frac{p_\theta(\boldsymbol{x}_{0}|\boldsymbol{x}_{1})}{q(\boldsymbol{x}_{1}|\boldsymbol{x}_{0})} \right] \\
&= E_{q(\boldsymbol x_{0:T})}\left[ -\log \frac{p(\boldsymbol{x}_T)}{q(\boldsymbol{x}_{T}\mid\boldsymbol{x}_{0})} - \sum_{t=2}^T\log\frac{p_\theta(\boldsymbol{x}_{t-1}|\boldsymbol{x}_{t})}{q(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_{t},\boldsymbol{x}_{0})}-\log p_\theta(\boldsymbol{x}_{0}|\boldsymbol{x}_{1}) \right] \\
&= E_{q(\boldsymbol x_{0:T})}\left[ D_{\mathrm{KL}}\left(q(\boldsymbol{x}_{T}\mid\boldsymbol{x}_{0})\parallel  p(\boldsymbol{x}_T) \right) 
+ \sum_{t=2}^T D_{\mathrm{KL}}(q(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_{t},\boldsymbol{x}_{0}) \parallel p_\theta(\boldsymbol{x}_{t-1}|\boldsymbol{x}_{t}) )
-\log p_\theta(\boldsymbol{x}_{0}|\boldsymbol{x}_{1})\right] \\
&= L_T + \sum_{t=2}^T L_{t-1} + L_0, \\
\end{aligned}

ここで次のように定義した。

\begin{aligned}
L_T &:= E_{q(\boldsymbol x_{0:T})}\left[ D_{\mathrm{KL}}\left(q(\boldsymbol{x}_{T}\mid\boldsymbol{x}_{0})\parallel  p(\boldsymbol{x}_T) \right)  \right], \\
L_{t-1} &:= E_{q(\boldsymbol x_{0:T})}\left[  D_{\mathrm{KL}}(q(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_{t},\boldsymbol{x}_{0}) \parallel p_\theta(\boldsymbol{x}_{t-1}|\boldsymbol{x}_{t}) ) \right], \\
L_0 &:= E_{q(\boldsymbol x_{0:T})}\left[ -\log p_\theta(\boldsymbol{x}_{0}|\boldsymbol{x}_{1})\right]
\end{aligned}

2行目から3行目の変形には以下の式を用いた。

\begin{aligned}
q(\boldsymbol{x}_{t}|\boldsymbol{x}_{t-1}) 
&= q(\boldsymbol{x}_{t}|\boldsymbol{x}_{t-1}, \boldsymbol{x}_{0}) \\
&= \frac{q(\boldsymbol{x}_{t},\boldsymbol{x}_{t-1},\boldsymbol{x}_{0})}{q(\boldsymbol{x}_{t-1},\boldsymbol{x}_{0})}\\
&= \frac{q(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_{t},\boldsymbol{x}_{0})q(\boldsymbol{x}_{t},\boldsymbol{x}_{0})}{q(\boldsymbol{x}_{t-1},\boldsymbol{x}_{0})}\\
&= \frac{q(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_{t},\boldsymbol{x}_{0})q(\boldsymbol{x}_{t}\mid\boldsymbol{x}_{0})}{q(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_{0})}\\
\end{aligned}

また、$q(\boldsymbol x_{t-1}\mid\boldsymbol x_{t},\boldsymbol x_{0})$は次のように表せる。

\begin{aligned}
q(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_{t},\boldsymbol{x}_{0}) 
&= \frac{q(\boldsymbol{x}_{t} \mid \boldsymbol{x}_{t-1})q(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_{0})}{q(\boldsymbol{x}_{t} \mid \boldsymbol{x}_{0})}
\end{aligned}

$\boldsymbol{x}_{t-1}$は分子のみに含まれるので、分子のみ考えれば良い。

\begin{aligned}
q(\boldsymbol{x}_{t} \mid \boldsymbol{x}_{t-1})q(\boldsymbol{x}_{t-1} \mid \boldsymbol{x}_{0})
&= \mathcal N(\boldsymbol{x}_{t}; \sqrt{\alpha_t}\boldsymbol{x}_{t-1} , \beta_t I)\mathcal N(\boldsymbol{x}_{t-1}; \sqrt{\bar\alpha_{t-1}}\boldsymbol{x}_{0} , (1-\bar\alpha_{t-1}) I)
\end{aligned}

指数部分のみ注目する。

\begin{aligned}
&\frac{1}{\beta_t}(\boldsymbol{x}_{t} - \sqrt{\alpha_t}\boldsymbol{x}_{t-1})^2 + \frac{1}{1-\bar\alpha_{t-1}}(\boldsymbol{x}_{t-1} - \sqrt{\bar\alpha_{t-1}}\boldsymbol{x}_{t-1})^2 \\
&=\left( \frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar\alpha_{t-1}} \right) \boldsymbol{x}_{t-1}^2 -2\left( \frac{\sqrt{\alpha_t}}{\beta_t}\boldsymbol{x}_{t} + \frac{\sqrt{\bar\alpha_{t-1}}}{1-\bar\alpha_{t-1}}\boldsymbol{x}_{0}\right)\cdot \boldsymbol{x}_{t-1} + (\mathrm{ not \ depend} \ \boldsymbol{x}_{t-1})
\end{aligned}

第一項の係数について、

\begin{aligned}
\frac{\alpha_t}{\beta_t}+\frac{1}{1-\bar\alpha_{t-1}}
&=\frac{\beta_t+\alpha_t(1-\bar\alpha_{t-1})}{\beta_t(1-\bar\alpha_{t-1})}\\
&=\frac{1-\alpha_t+\alpha_t-\bar\alpha_{t}}{\beta_t(1-\bar\alpha_{t-1})}\\
&=\frac{1-\bar\alpha_{t}}{\beta_t(1-\bar\alpha_{t-1})}\\
\end{aligned}

これらより、$\boldsymbol{x}_{t-1}$のガウス分布の平均と分散がわかる。

\begin{aligned}
q(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_{t},\boldsymbol{x}_{0}) &= \mathcal N(\boldsymbol{x}_{t-1}; \boldsymbol{\tilde \mu}_t(\boldsymbol{x}_{t}, \boldsymbol{x}_{0}),\tilde \beta_t I)\\
\tilde \beta_t &= \frac{\beta_t(1-\bar\alpha_{t-1})}{1-\bar\alpha_{t}} \\
\boldsymbol{\tilde \mu}_t(\boldsymbol{x}_{t},\boldsymbol{x}_{0}) 
&= \frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})}{1-\bar\alpha_{t}}\boldsymbol{x}_{t} + \frac{\beta_t\sqrt{\bar\alpha_{t-1}}}{1-\bar\alpha_{t}}\boldsymbol{x}_{0}
\end{aligned}

以上で目的関数を評価できる。$L_T,L_{1:T-1},L_0$の意味について考察する。

$L_{T}$について考える。

\begin{aligned}
L_T &= D_{\mathrm{KL}}\left(q(\boldsymbol{x}_{T}\mid\boldsymbol{x}_{0})\parallel  p(\boldsymbol{x}_T) \right), \\
q(\boldsymbol{x}_{T}\mid\boldsymbol{x}_{0}) &= \mathcal N(\boldsymbol{x}_{T};\sqrt{\bar \alpha_T}\boldsymbol{x}_{0}, (1-\bar\alpha_T)I ),\\
p(\boldsymbol{x}_T) &= \mathcal N(\boldsymbol{x}_{T}; \boldsymbol{0}, I).
\end{aligned}

$\beta_t$を定数として学習しないとすると、$L_T$は学習するパラメータがない。したがって$L_T$は定数であり、目的関数から除外できる。

$L_{t-1},(t=2,3,\cdots,T)$について考える。

\begin{aligned}
L_{t-1} &= D_{\mathrm{KL}}(q(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_{t},\boldsymbol{x}_{0}) \parallel p_\theta(\boldsymbol{x}_{t-1}|\boldsymbol{x}_{t}) ),\\
q(\boldsymbol{x}_{t-1}\mid\boldsymbol{x}_{t},\boldsymbol{x}_{0}) &= \mathcal N(\boldsymbol{x}_{t-1}; \boldsymbol{\tilde \mu}_t(\boldsymbol{x}_{t}, \boldsymbol{x}_{0}),\tilde \beta_t I),\\
p_\theta(\boldsymbol{x}_{t-1}|\boldsymbol{x}_{t}) &= \mathcal N(\boldsymbol{x}_{t-1}; \boldsymbol{\mu}_\theta(\boldsymbol{x}_t, t), \Sigma_\theta(\boldsymbol{x}_{t}, t)).
\end{aligned}

分散$\Sigma_\theta(\boldsymbol{x}_{t}, t)$は定数に固定し、学習しない。

\begin{aligned}
\Sigma_\theta(\boldsymbol{x}_{t},t) = \sigma_t^2 I
\end{aligned}

$\sigma_t^2$の極端な選び方として、$\sigma_t^2=\beta_t$と$\sigma_t^2=\tilde \beta_t$の二つがある。前者は$\forall \alpha_s=0$を意味するので、すなわち$\boldsymbol x_{0}\sim \mathcal N(\boldsymbol{0}, I)$と設定されているときに最適である。後者は$\boldsymbol x_{0}$を決定論的に1点に設定したときに最適である（abeTコメント：ここの意味がわからない）。実験的にはどちらを選んでもあまり変わらない。

$L_{t-1}$に分布を代入して、次の式を得る。

\begin{aligned}
L_{t-1} &= E_{q(\boldsymbol x_{0:T})} \left[ \frac{1}{2\sigma_t^2}\| \boldsymbol{\tilde \mu}_t(\boldsymbol{x}_{t}, \boldsymbol{x}_{0}) - \boldsymbol{\mu}_\theta(\boldsymbol{x}_t, t) \|^2 \right] + C.
\end{aligned}

$C$は$\theta$ に依存しない項である。$\boldsymbol {\tilde\mu_t}(\boldsymbol x_{t}, \boldsymbol{x}_{0})$は$\boldsymbol x_t$と$\boldsymbol x_0$で具体的に書ける。また、$\boldsymbol x_0$は$\boldsymbol x_t$と$ \boldsymbol \varepsilon$で書くことができる。

\begin{aligned}
\boldsymbol{x}_{0} = \frac{1}{\sqrt{\bar\alpha_t}}\left(\boldsymbol{x}_{t} (\boldsymbol{x}_{0},\boldsymbol \varepsilon) - \sqrt{1 - \bar\alpha_t} \boldsymbol \varepsilon\right)
\end{aligned}

これらを組み合わせて次の式を得る。

\begin{aligned}
\boldsymbol{\tilde \mu}_t(\boldsymbol{x}_{t}(\boldsymbol{x}_{0},\boldsymbol \varepsilon), \boldsymbol{x}_{0})
&= \frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})}{1-\bar\alpha_{t}}\boldsymbol{x}_{t} (\boldsymbol{x}_{0},\boldsymbol \varepsilon)+ \frac{\beta_t\sqrt{\bar\alpha_{t-1}}}{1-\bar\alpha_{t}}\boldsymbol{x}_{0} \\
&= \frac{\sqrt{\alpha_t}(1-\bar\alpha_{t-1})}{1-\bar\alpha_{t}}\boldsymbol{x}_{t} (\boldsymbol{x}_{0},\boldsymbol \varepsilon) + \frac{\beta_t\sqrt{\bar\alpha_{t-1}}}{1-\bar\alpha_{t}}\left( \frac{1}{\sqrt{\bar\alpha_t}}\left(\boldsymbol{x}_{t} (\boldsymbol{x}_{0},\boldsymbol \varepsilon) - \sqrt{1 - \bar\alpha_t} \boldsymbol \varepsilon\right)\right) \\
&= \frac{1}{\sqrt{\alpha_t}}\left(\boldsymbol{x}_{t} (\boldsymbol{x}_{0},\boldsymbol \varepsilon) - \frac{\beta_t}{\sqrt{1-\bar\alpha_t}} \boldsymbol \varepsilon \right)
\end{aligned}

一方で、$\boldsymbol{\mu}_\theta(\boldsymbol{x}_t, t)$を次のようにパラメトライズする。

\begin{aligned}
\boldsymbol{\mu}_\theta (\boldsymbol{x}_t, t) 
&:= \boldsymbol{\tilde \mu}_t\left(\boldsymbol{x}_{t}, \frac{1}{\sqrt{\bar\alpha_t}}\left(\boldsymbol{x}_{t}  - \sqrt{1 - \bar\alpha_t} \boldsymbol \varepsilon_\theta(\boldsymbol{x}_{t},t)\right)\right) \\
&= \frac{1}{\sqrt{\alpha_t}}\left(\boldsymbol{x}_{t}  - \frac{\beta_t}{\sqrt{1-\bar\alpha_t}} \varepsilon_\theta(\boldsymbol{x}_{t},t) \right)
\end{aligned}

$\boldsymbol\varepsilon_\theta(\boldsymbol x_{t})$は$\boldsymbol x_{t}$を入力して$\boldsymbol\varepsilon$を予測する関数である。したがってリバース・プロセスのサンプリングプロセス$\boldsymbol x_{t-1}\sim p(\boldsymbol x_{t-1}\mid \boldsymbol x_{t})$は次のように書ける。

\begin{aligned}
\boldsymbol x_{t-1} &= \frac{1}{\sqrt{\alpha_t}}\left(\boldsymbol{x}_{t}  - \frac{\beta_t}{\sqrt{1-\bar\alpha_t}} \varepsilon_\theta(\boldsymbol{x}_{t}) \right) + \sigma_t \boldsymbol{z}, \\
\boldsymbol{z} &\sim \mathcal N(\boldsymbol{0}, I).
\end{aligned}

さて、得られた$\boldsymbol{\tilde \mu_t} (\boldsymbol x_t(\boldsymbol x_0,\boldsymbol \varepsilon), \boldsymbol x_0)$と$\boldsymbol \mu_\theta (\boldsymbol x_t, t)$を$L_{t-1}$に代入する。

\begin{aligned}
L_{t-1} - C &= E_{\boldsymbol x_{t}, \varepsilon} \left[ \frac{\beta_t^2}{2\sigma_t^2 \alpha_t(1-\bar\alpha_t)}\| \boldsymbol{\varepsilon} -  \boldsymbol{\varepsilon}_\theta(\boldsymbol{x}_t, t) \|^2 \right]\\
&= E_{\boldsymbol x_{0}, \varepsilon} \left[ \frac{\beta_t^2}{2\sigma_t^2 \alpha_t(1-\bar\alpha_t)}\| \boldsymbol{\varepsilon} -  \boldsymbol{\varepsilon}_\theta(\sqrt{\bar\alpha_t}\boldsymbol x_0+\sqrt{1-\bar\alpha_t}\boldsymbol{\varepsilon}, t) \|^2 \right].
\end{aligned}

この式は tでインデックスされた denoising score matching over multiple noise scales に似ている。また、一部はLangevin-like reverse process の変分バウンドと一致している。

まとめると、リバース・プロセスは$\boldsymbol {\tilde\mu_t}$を予測するよう$\boldsymbol \mu_\theta(\boldsymbol x_t, \boldsymbol x_0)$を訓練するか、$\boldsymbol {\varepsilon}$を予測するよう$\boldsymbol {\varepsilon}_\theta(\boldsymbol x_t)$を訓練すればよい。実際の訓練では、係数を無視した次を目的関数とする。

\begin{aligned}
L_{t-1}^{\mathrm{simple}} = E_{\boldsymbol x_{0}, \varepsilon} \left[\| \boldsymbol{\varepsilon} -  \boldsymbol{\varepsilon}_\theta\left(\sqrt{\bar\alpha_t}\boldsymbol x_0+\sqrt{1-\bar\alpha_t}\boldsymbol{\varepsilon}, t\right) \|^2 \right].
\end{aligned}

係数を無視した場合、無視する前と比べて$t$が小さいときの重みが小さくなる。すると、$t$が大きい難しいデノイズの訓練に集中するようになり、有益である。

最後に$L_0$について考える。

\begin{aligned}
L_0 &= E_{q(\boldsymbol x_{0:T})} \left[ -\log p_\theta(\boldsymbol x_0\mid \boldsymbol x_1) \right].
\end{aligned}

前提として、画像データの画素値{0,1,...,255}は{-1,1}にスケールされているとする。これは$p(\boldsymbol x_T)$が標準正規分布であることにも整合的である。離散対数尤度を得るために、リバース・プロセスの最後の変換を$\mathcal N(\boldsymbol x_0; \boldsymbol \mu_\theta(\boldsymbol x_1, 1), \sigma_1^2 I)$から得られる独立な離散デコーダに設定する。

\begin{aligned}
p_\theta(\boldsymbol x_0\mid \boldsymbol x_1) &= \prod_{i=1}^D \int_{\delta_-(x_0^i)}^{\delta_+(x_0^i)} \mathcal N(x; \boldsymbol \mu_\theta(\boldsymbol x_1, 1), \sigma_1^2 I) dx, \\
\delta_+(x) &= \left\{
\begin{array}{ll}
\infty & (x = 1)\\
x+\frac{1}{255} & (x < 1)
\end{array}
\right.
,\\
\delta_-(x) &= \left\{
\begin{array}{ll}
-\infty & (x = -1)\\
x-\frac{1}{255} & (x > -1)
\end{array}
\right.
.
\end{aligned}

ここで、$D$ はデータの次元数であり、添え字の $i$ は1つの座標値を示す。VAEデコーダや自己回帰モデルで用いられる離散化された連続分布と同様に、データにノイズを加えたり、スケーリング操作のヤコビアンを対数尤度に取り込む必要がなく、変分境界が離散データのロスレスコード長になることを保証するものである。
結局$L_0$の最小化は、リバース・プロセスの最後の変換が$\boldsymbol x_0$に一致するように訓練すれば良い。

評価

実験設定

• $T=1000$。
• $\beta_t$は$\beta_1=10^{-4}, \beta_T=0.02$になるように線形に設定。
• リバース・プロセスには PixelCNN++²を踏襲し、U-Net backbon with group normalization を使用。ネットワークのweightは時間$t$に渡って共有する。
• 拡散時間$t$は、各残差ブロックにTransformerの正弦波位置埋め込みを加えることで指定する。

評価方法

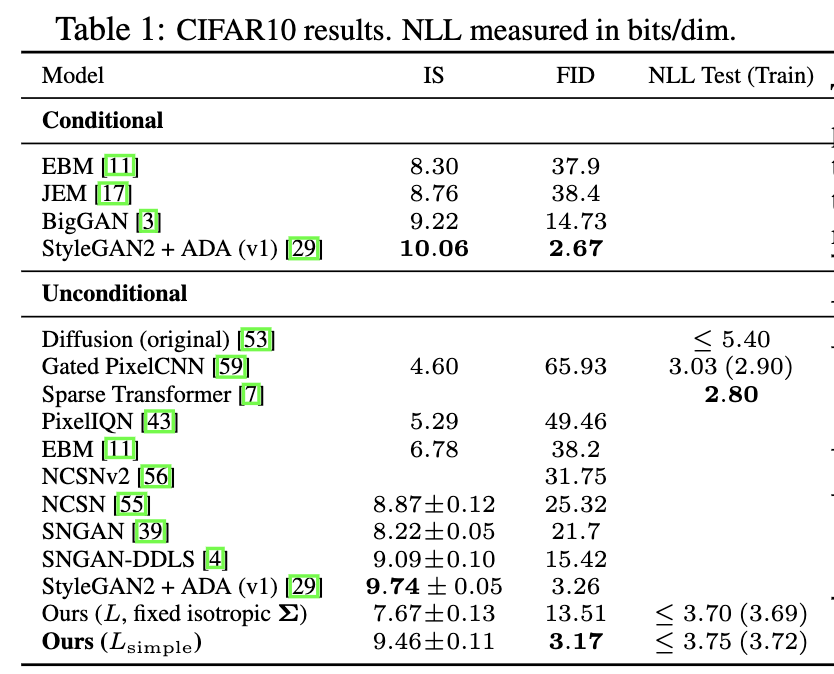
• Inception scores, FID scores, and negative log likelihoods を用いて評価。
• CIFAR10の結果ではFID score で良好な結果となった。

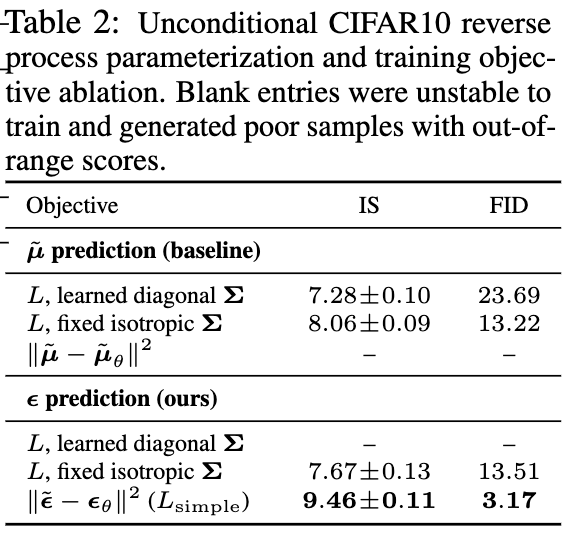
• 訓練に$\boldsymbol \mu$と$\boldsymbol \varepsilon$のどちらを使用すると良いか比較。$\boldsymbol \varepsilon$を使用して、$\beta_t$を固定し、単純化した目的関数を使用することで高品質な画像を生成できる。

生成された画像

まとめ・感想

まとめ

• 拡散確率モデルを用いた高品質な画像合成手法を提案。
• フォワード・プロセスは学習が不要。
• ノイズ$\boldsymbol \varepsilon$を予測する方が精度が出る。
• CIFARの学習は8個のV100 GPUs相当の計算力で、バッチサイズ128、800k step学習させた。1秒で21step処理できるので、学習には約10.6時間かかる。

感想

• 微小ノイズ除去を有限回繰り返して画像を生成する発想が面白い。無限小変換を繰り返せば有限変換みたいな。
• CIFAR10 の解像度32×32で8個のV100 GPUsで10時間は自分でやるには手軽ではない。

1. Feller, William. “On the Theory of Stochastic Processes, with Particular Reference to Applications.” (1949). ↩

2. Tim Salimans, Andrej Karpathy, Xi Chen, and Diederik P Kingma. "PixelCNN++: Improving the PixelCNN with discretized logistic mixture likelihood and other modifications". In International Conference on Learning Representations, 2017. ↩