拡散モデルがモード崩壊しない理由

はじめに

GAN（Generative Adversarial Network; 敵対的生成ネットワーク）のモード崩壊は、訓練中のGANがデータセットの多様性全体を捉えることができず、限られた数のサンプルまたは非常に似ているサンプルのみを生成するときに発生する問題を指します。この問題はGANの訓練の難しさとしてよく知られています。

モード崩壊の原因としては次のようなものが考えられています。

• 敵対的なフィードバックの不均衡： 生成器が特定のサンプルをうまく生成できると、それを繰り返し生成することで識別器を欺くのが簡単になる場合があります。その結果、生成器はデータセットのその他の多様性を学ぶ動機を失うことがあります。
• 学習率の不均衡： 生成器と識別器の学習率や更新速度が不均衡であると、モード崩壊が発生しやすくなります。

一方、2023年に流行している拡散モデルではモード崩壊するといったことはほとんど聞きません。そこで本稿では、両モデルの損失関数の特徴からモード崩壊について考察します。

GANとJSダイバージェンス

GANは、生成モデルと識別モデルの2つのニューラルネットワークが対抗するように訓練される構造です。その基本的な目的関数は、実際にはJensen-Shannon (JS) ダイバージェンスに基づいています。ここで、JSダイバージェンスとは2つの確率分布の間の「距離」や「違い」を測定するものです。

具体的には、GANの訓練中、生成器$G$はデータの実際の分布$p_{\text{data}}$を模倣するような新しいデータ点を生成することを試みます。一方、識別器$D$は、入力されたデータが本物のデータ分布から来たものか、それとも生成器から来たものかを判断しようとします。

GANの目的関数は以下のように表現されます。

\begin{align}
\min_G \max_D V(D, G) = \mathbb{E}_{x \sim p_{\text{data}}(x)}[\log D(x)] + \mathbb{E}_{z \sim p_z(z)}[\log(1 - D(G(z)))]
\end{align}

ここで、

• $\mathbb{E}$ は期待値を示す。
• $x \sim p_{\text{data}}(x)$ は真のデータ分布からのサンプルである。
• $z \sim p_z(z)$ はランダムノイズからのサンプルで、これを生成器の入力として用いる。
• $D(x)$ は識別器によって $x$が実データとして認識される確率を示す。
• $G \sim p_g$ は生成器によって生成されたデータを示す。
• $D(G(z))$ は生成器によって生成されたデータが実データとして認識される確率を示す。

JSダイバージェンスは、二つの確率分布$p$と$q$の間に定義されます。

\begin{align}
\text{JS}(p || q) = \frac{1}{2} \text{KL}(p || m) + \frac{1}{2} \text{KL}(q || m)
\end{align}

ここで$m$は、

\begin{align}
m = \frac{1}{2} (p + q)
\end{align}

と定義されます。また、$\text{KL}$はKullback-Leibler (KL)ダイバージェンスです。

\begin{align}
\text{KL}(p || q) &= \sum_x p(x) \log \left( \frac{p(x)}{q(x)} \right)
\end{align}

以下の式は後の計算で使う式です。

\begin{align}
\text{KL}(p || m) &= \sum_x p(x) \log \left( \frac{p(x)}{p(x)+q(x)} \right)+\log2 \\
\text{KL}(q || m) &= \sum_x q(x) \log \left( \frac{q(x)}{p(x)+q(x)} \right)+\log2
\end{align}

GANの目的関数を最適化すると、生成分布$p_g$と実データの分布$p_\text{data}$の間のJSダイバージェンスを最小化する方向に進むことが示唆されています。しかし、目的関数が明示的にJSダイバージェンスの形になるわけではありません。

しかし、仮に識別器$D$が最適化された場合、つまり$D^\ast$が得られた場合、以下の関係が成り立ちます。

\begin{align}
D^\ast(x) = \frac{p_{\text{data}}(x)}{p_{\text{data}}(x) + p_g(x)}
\end{align}

この最適な識別器をGANの目的関数に代入して期待値を計算すると、その結果はJSダイバージェンスと関連する形になります。

\begin{align}
\min_G V(D^\ast, G) &= \mathbb{E}_{x \sim p_{\text{data}}(x)}[\log D^\ast(x)] + \mathbb{E}_{z \sim p_z(z)}[\log(1 - D^\ast(G(z)))] \\
&= \mathbb{E}_{x \sim p_{\text{data}}(x)}[\log D^\ast(x)] + \mathbb{E}_{G \sim p_g}[\log(1 - D^\ast(G))] \\
&= \sum_x p_{\text{data}}(x) \log\left( \frac{p_{\text{data}}(x)}{p_{\text{data}}(x) + p_g(x)} \right) + \sum_x p_g(x) \log\left( \frac{p_g(x)}{p_{\text{data}}(x) + p_g(x)} \right) \\
&= \text{KL}(p_{\text{data}} || \frac{p_{\text{data}}+p_g}{2})-\log2 + \text{KL}(p_g || \frac{p_{\text{data}}+p_g}{2})-\log2 \\
&= 2\text{JS}(p_{\text{data}} || p_g) - 2\log2
\end{align}

要するに、GANの目的関数自体が直接的にJSダイバージェンスではありませんが、識別器が最適化されたときの期待値の関係から、生成分布と実データの分布のJSダイバージェンスを最小化する方向に進むことが示唆されています。

拡散モデルとKLダイバージェンス

拡散モデルは最尤推定（Maximum Likelihood Estimation; MLE）でニューラルネットワークのパラメータを推定します。

最尤推定の基本的な考え方は、与えられたデータセット$\mathcal{D}$ に対して、パラメータ$\theta$を持つモデル$p(x | \theta)$ の尤度を最大化するパラメータ$\theta$ を見つけることです。この尤度は以下のように定義されます。

\begin{align}
L(\theta | \mathcal{D}) = \prod_{i=1}^{N} p(x_i | \theta)
\end{align}

ここで、$x_i$ はデータセットの$i$番目のサンプルを示します。

尤度関数を最大化する代わりに、負の対数尤度関数を最小化することが一般的です。これは計算が簡単で、同じパラメータ $\theta$ を得るからです。

\begin{align}
- \log L(\theta | \mathcal{D}) = - \sum_{i=1}^{N} \log p(x_i | \theta)
\end{align}

一方、KLダイバージェンスは、二つの確率分布 $p$ と $q$ の「距離」を測るための尺度です。これは以下のように定義されます。

\begin{align}
\text{KL}(p || q) = \sum_x p(x) \log \left( \frac{p(x)}{q(x)} \right)
\end{align}

データの真の分布を $p_{\text{data}}(x)$ 、モデルの分布を $ p_g(x | \theta) $ とすると、以下の式を得ます。

\begin{align}
\sum_x\text{KL}(p_{\text{data}} || p_g(x | \theta)) &= \sum_x p_{\text{data}}(x) \log \left( \frac{p_{\text{data}}(x)}{p_g(x | \theta)} \right) \\
&= -\sum_x p_{\text{data}}(x) \log p_g(x | \theta) + (\theta \ \text{independent})
\end{align}

この式は、真の分布とモデル分布との間のKLダイバージェンスを示しています。右辺第一項は負の対数尤度になっています。したがって最尤推定の目的は、KLダイバージェンスを最小化することと等価です。

KLダイバージェンス最小化とJSダイバージェンス最小化の違い

拡散モデルの目的関数であるKLダイバージェンスについて考えます。式は次の通りです。

\begin{align}
\text{KL}(p_{\text{data}} || p_g) = \sum_x p_{\text{data}}(x) \log \left( \frac{p_{\text{data}}(x)}{p_g(x)} \right)
\end{align}

まず、上記のKLダイバージェンスは $p_{\text{data}}(x)>0$ の領域のみが損失として有効です。したがって、$p_{\text{data}}(x)$が小さい領域の $p_g(x)$ はうまく学習できません。したがって、$p_{\text{data}}(x)$ が多峰の場合、モード周辺はよく学習される一方、$p_{\text{data}}(x)\sim 0$の領域では密度関数の値が小さくなるように学習されません（密度関数は積分すると1なのでモードを学習すると相対的に他の領域の値は小さくなりますが）。したがって、各モードを学習しつつ、学習データがない領域の多様な画像も生成できるモデルになります。

GANの目的関数であるJSダイバージェンスについて考えます。

\begin{align}
\text{JS}(p_{\text{data}} || p_g)  = \frac{1}{2}\sum_x p_{\text{data}}(x) \log\left( \frac{2p_{\text{data}}(x)}{p_{\text{data}}(x) + p_g(x)} \right) + \frac{1}{2} \sum_x p_g(x) \log\left( \frac{2p_g(x)}{p_{\text{data}}(x) + p_g(x)} \right) \\
\end{align}

右辺第一項は、$p_{\text{data}}(x)>0$ の領域で $p_g=p_{\text{data}}$にしようとする最尤推定と同様な働きを持つことが示唆されています。

右辺第二項が効いてくるのは$p_g(x)>0$ の領域です。$p_g(x)$が小さい領域ではうまく学習できません。つまり、一度$p_g(x)\sim 0$となると第二項はほぼ$0$のまま学習が進まなくなります。したがって、モデル分布の密度関数の値が小さく、かつ真のデータ分布で相対的に他のモードよりも小さいモード領域のモデル分布の密度関数の値が小さくなります。このように学習が進んでしまい、真のデータ分布の多峰性を学習できず、モデル分布が単峰になってしまうのがモード崩壊です。

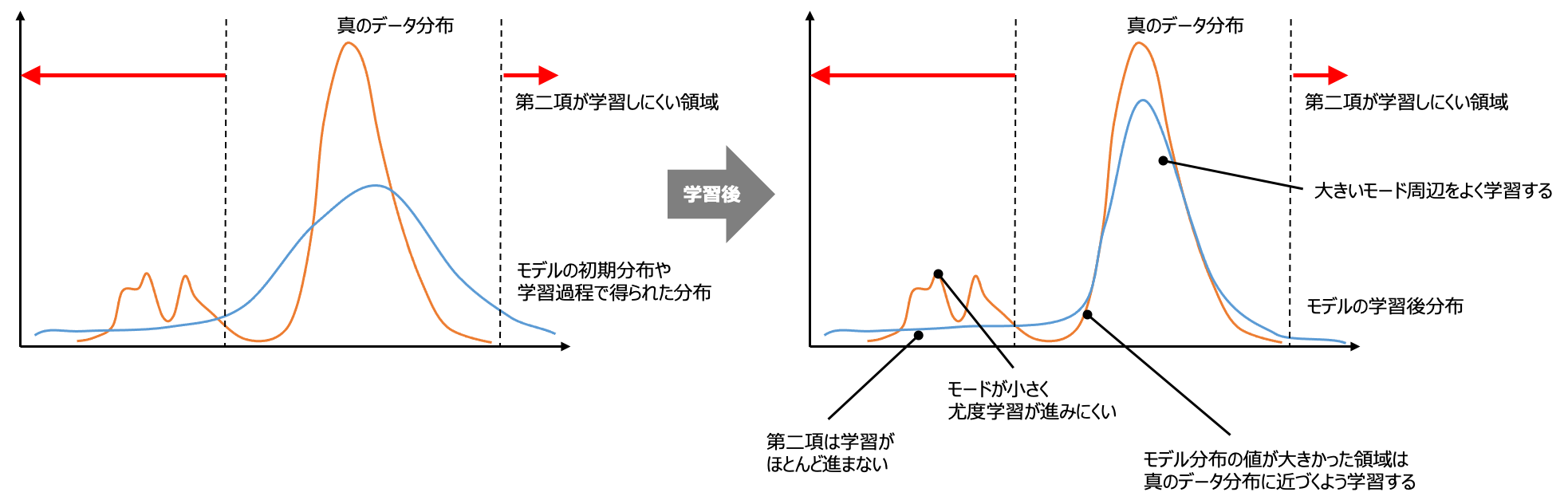
学習メカニズムの観点からは、モード崩壊は生成器が識別機をうまく騙せた画像、すなわち生成器が過去に生成したことがある画像ばかりを生成するようになってしまう事象と理解できます。

また、生成器と識別器の学習率や更新速度が不均衡であるとモード崩壊が発生しやすくなる理由ですが、これは生成器が十分学習されないうちに識別器の能力が上がりすぎてしまうことが原因と考えます。これは次のように理解できるのではないでしょうか。

今まで真のデータ分布のポンチ絵を描いてきましたが、実際のデータ分布は離散的でデルタ関数の和で書けるような分布になっています。このような分布では最尤推定が学習可能な領域が非常に狭く、学習がほとんど進まないように思えます。

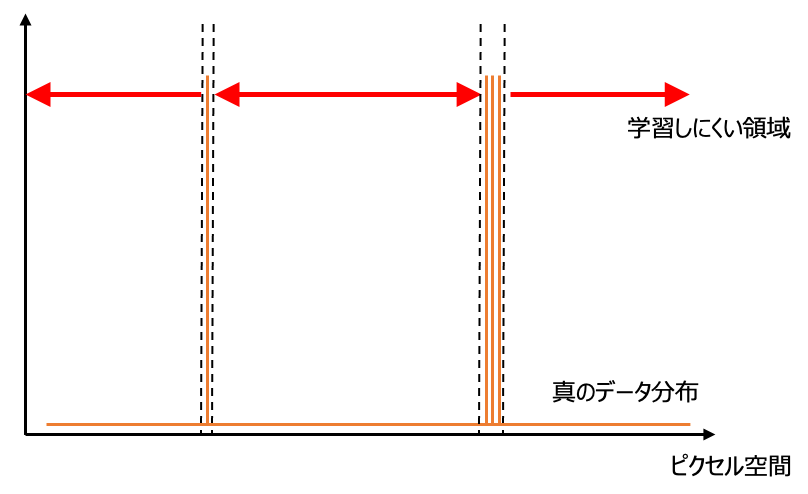
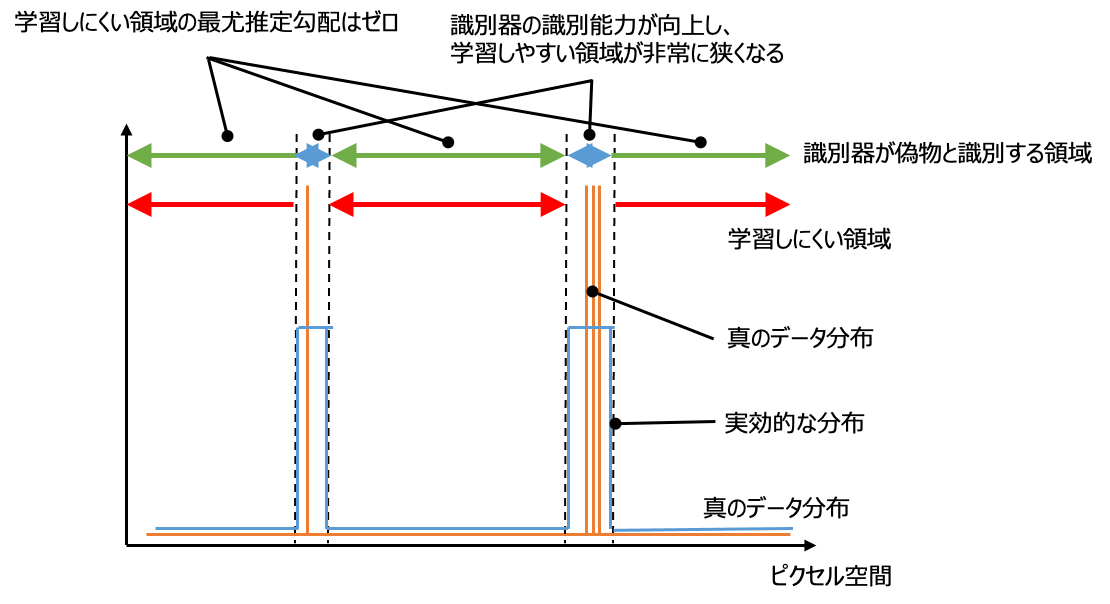
しかし、GANの学習において、生成器に対して実際にフィードバックを行っているのは分布の密度関数$p_\text{data}$ではなく、識別器が識別できたかどうかです。つまり、識別器の識別能力が低ければ、生成器にとって真のデータ分布はもっと広がりのあるものとして捉えられることになります。

識別器の識別能力が向上、もといオーバーフィットし、真のデータ分布と寸分違わないもののみを本物と識別するようになってしまうと、学習しにくい領域が大きくなってしまいます。その領域だとどんな画像を生成しても偽物と判定されてしまい、生成器にフィードバックが与えられなくなってしまいます。すなわち勾配が消失してしまいます。これにより、過去に生成してうまく騙せた画像ばかり生成するようになってしまいモード崩壊が起きると考えられます。

GANのモード崩壊の対策

Minibatch Discrimination

T. Salimans, I. Goodfellow, W. Zaremba, V. Cheung, A. Radford, and X. Chen, “Improved techniques for training GANs,” Advances in neural information processing systems, pp.2234–2242, 2016.

モード崩壊を起こさないためには、類似した画像の生成をしないように生成器に教えてあげればよいです。Minibatch Discriminationでは、ミニバッチ内の生成画像の近さを定量化します。定量化した量を、識別器の識別結果とともに生成器にフィードバックします。生成器は、モード崩壊が原因による識別のしやすさを学習し、識別しにくい、ばらつきのあるデータを生成しようと学習します。

WGAN-GP （Wasserstein GAN with Gradient Penalty）

I. Gulrajani, F. Ahmed, M. Arjovsky, V. Dumoulin, and A. Courville, “Improved training of Wasserstein GANs,” Advances in Neural Information Processing Systems, pp.5768-5778, 2017.

WGANは識別器（またはクリティック）が1-リプシッツ連続であることを要求します。初期のWGANのアプローチは、この条件を満たすために識別器の重みをクリッピングする方法を使用していましたが、この方法は訓練の不安定性や他の問題を引き起こす可能性がありました。

WGAN-GPでは、この1-リプシッツ条件を強制するために、勾配ペナルティを使用しています。具体的には、識別器の勾配のノルムが1であることを目指します。

Spectral Normalization

T. Miyato, T. Kataoka, M. Koyama, and Y. Yoshida. Spectral normalization for generative adversarial networks. In Int’l Conf. on Learning Representations, 2018.

重み行列の最大固有値でその重みをスケーリングすることで、リプシッツ条件を満たすように制約をかけます。
この制約は、特にWGANなどでのリプシッツ条件の満足を容易にし、モード崩壊のリスクを減少させる効果があります。

entropy-regularized adversarial loss

Adji B. Dieng, Francisco J. R. Ruiz, David M. Blei, Michalis K. Titsias, "Prescribed Generative Adversarial Networks," https://arxiv.org/abs/1910.04302

モード崩壊を起こさないためには、画像生成分布$p_g$に広がりを持たせればよいです。そこで、$p_g$のばらつきの指標であるエントロピーを目的関数に加えて、正則化します（エントロピー正則化）。

訓練スキームの改良

• 生成器と識別器の更新の比率調整
  典型的なGANでは、各エポックで識別器を1回、生成器を1回更新するのが一般的です。しかし、識別器を複数回更新してから生成器を1回更新するというスキームを使用することで、訓練の安定性を向上させることができる場合があります。

• 学習率のスケジューリング
  固定の学習率ではなく、訓練の進行とともに学習率を動的に変更することで、訓練の収束を促進させることができることがあります。

• 様々な正規化テクニックの採用
  例えば、バッチ正規化やスペクトル正規化などの正規化手法を導入することで、訓練の安定性を向上させることができます。

• 別の損失関数の試行
  WGANやLSGANなど、標準的なGANの損失関数以外の損失関数を使用することで、訓練の安定性や生成結果の質を向上させることが報告されています。

• コンシステント性の確保
  生成器の出力が微小な変化に対して一貫性を持つようにする手法も考えられます。

• 早期終了
  訓練を適切なタイミングで停止し、過学習を防ぐための戦略も訓練スキームの一部として考えることができます。

まとめ

拡散モデルがモード崩壊しないのは最尤推定だから。

参考文献

• 岡野原大輔, 『拡散モデル データ生成技術の数理』, 岩波書店, 2023/02/17, ISBN: 9784000063432.

• Ainur Gainetdinov, "GAN Mode Collapse Explanation", https://pub.towardsai.net/gan-mode-collapse-explanation-fa5f9124ee73

• @SZZZUJg97M, "GANの正規化手法Spectral Normalizationを理解する", https://qiita.com/SZZZUJg97M/items/371f694f05998439bd45

• 株式会社アイビス, "エントロピー正則化でモード崩壊を抑制！Prescribed GANのアイデアを解説", https://www.ibis.ne.jp/blog/deeplearning1613/