【Python】期待値最大化 (EM) アルゴリズム

期待値最大化 (EM) アルゴリズム

　期待値最大化 (EM) アルゴリズムは、潜在変数を持つ確率モデルで最尤推定する方法の一つである。

EM アルゴリズムの背後にある基本的な考え方は、次の 2 つのステップを交互に繰り返すことにより、潜在変数の推定値を繰り返し調整すること。

• 期待 (E) ステップ: 潜在変数の現在の推定値を使用して、完全なデータの対数尤度の期待値を計算する

• 最大化 (M) ステップ: E ステップからの期待値を使用して、モデル パラメーターに関して完全なデータの尤度(対数尤度)を最大化する

　これらの 2 つの手順は、Q関数の値が収束条件に達するまで繰り返す。 EM アルゴリズムは、直接的な最尤推定が困難または不可能な状況で特に役立つ。

　つまり、EM アルゴリズムは、完全データの対数尤度の期待値の推定とモデルに関する完全データの対数尤度の最大化を交互に行うことにより、潜在変数を持つモデルの最尤推定値を見つけるための反復法です。

EMアルゴリズムの処理の流れ

Expectation-Maximization（EM）アルゴリズムの処理の流れを簡潔に説明します。

1. モデルパラメータを初期推定値で初期化する。
2. Eステップ：パラメータの現在の推定値から完全データ対数尤度の期待値を計算する。
3. Mステップ：Eステップで得られた期待値を用いて、完全データ対数尤度をモデルパラメータに関して最大化する。
4. 収束までEステップとMステップを繰り返す。収束は、対数尤度の変化がある閾値以下になったこと、または最大反復回数に達したことを意味する。
5. EMアルゴリズムの結果として、パラメータの最終推定値が得られる。

このプロセスは、EステップとMステップを収束するまで繰り返すというループを表すことができます。

ソースコード

二次元で3つのガウス分布が混ざった疑似データでのガウス分布のパラメーター推定

EM_Algorithm.py

import numpy as np
from matplotlib import pyplot
import matplotlib.animation as animation
import sys

# K個のガウス分布に従う乱数サンプルをN/K個生成する
# Xが各ガウス分布のサンプル、mu_listがガウス分布の平均値、sigma_listが分散のリスト
def create_data(N, K):
    X, mu_list, sigma_list = [], [], []
    for i in range(K):
        loc = (np.random.rand() - 0.7) * 10.0 # 平均 (i+1) * 4     
        scale = 1  # 標準偏差
        # ガウス分布からサンプリングされたデータリスト
        X = np.append(X, np.random.normal(
            loc = loc, # 平均
            scale = scale, # 標準偏差
            size = int(N / K) # 出力配列のサイズ
        ))
        # 平均のデータリスト
        mu_list = np.append(mu_list, loc)
        # 標準偏差のデータリスト
        sigma_list = np.append(sigma_list, scale)
    return (X, mu_list, sigma_list)

# 平均値mu、分散sigmaのガウス分布の関数を返す
def gaussian(mu, sigma):
    def f(x):
        return np.exp(-0.5 * (x - mu) ** 2 / sigma ** 2) / np.sqrt(2 * np.pi * sigma ** 2)
    return f

# Eステップにおいて事後確率を計算する
# いわゆる新しいデータ点を踏まえて、観測者により決めれる提案分布により、確率分布の形状を変化させている
# 今回はサンプリング手法のため、乱数で新しいデータを生成している
# そのため、提案分布も始めはランダムな分布をしてしている。
# 事後確率をベイズの定理から計算しており、
# 事前分布 l(x)と尤度関数(提案分布) piをかけて、事後分布を求めている
def Expectatoin_Step(X, pi, gf):
    l = np.zeros((X.size, pi.size))
    for (i, x) in enumerate(X):
        # gfはガウシアン関数で、入力xに対して、正規分布に従う乱数を生成している
        l[i, :] = gf(x)
    # piとlの要素ごとの積: 事前分布 l(x)と尤度関数(提案分布) piをかけて、事後分布を求めている
    numerator = pi * l
    # piとlの要素ごとに積の和を計算: 正規化
    denominator = np.vectorize(lambda y: y)((l*pi).sum(axis=1).reshape(-1, 1))
    return numerator / denominator


# MステップにおいてQ関数を最大化するパラメタ mu, sigma, pi を計算する
# 混合ガウス分布においては、最大値は解析解が求められるので、数値計算で得られる
def Maximization_Step(X, post_pro):
    N = post_pro.sum(axis=0)
    mu = (post_pro * X.reshape((-1, 1))).sum(axis=0) / N
    sigma = np.sqrt((post_pro * (X.reshape(-1, 1) - mu) ** 2).sum(axis=0) / N)
    pi = N / X.size
    return (mu, sigma, pi)


# Q関数を計算する
# 尤度関数の場合、ここはそのまま尤度関数になる。
# 計算の都合上、対数尤度関数を用いることが多く、
# -0.5*(y-u)**2/(2.0*sigma**2)で計算される
def calc_Q(X, mu, sigma, pi, post_pro):
    Q = (post_pro * (np.log(pi * (2 * np.pi * sigma ** 2) ** (-0.5)))).sum()
    for (i, x) in enumerate(X):
        Q += (post_pro[i, :] * (-0.5 * (x - mu) ** 2 / sigma ** 2)).sum()
    return Q


if __name__ == '__main__':
    np.random.seed(1234)

    K = 3 # サンプルデータのガウス分布の数(山の数)
    N = 1500 * K # サンプルデータの総数
    # 疑似サンプルデータ
    X, mu_list, sigma_list = create_data(N, K)

    colors = ['r', 'b', 'g']

    # 収束条件：残差がepsilonより小さくなったら、ループを終わる
    epsilon = 1e-12

    # 未知パラメタを初期化する
    pi = np.random.rand(K)
    mu = np.random.randn(K)
    sigma = np.abs(np.random.randn(K))
    Q = -sys.float_info.max
    delta = None

    ims = []
    fig = pyplot.figure()

    # 疑似サンプルデータをプロット
    n, bins, _ = pyplot.hist(X, 100, density=True, alpha=0.3)

    # プロットするときの横軸のビン数
    seq = np.arange(-15, 15, 0.02)

    index = 0

    # EMアルゴリズム
    while delta == None or delta >= epsilon:
        # ガウス分布に従うデータ生成用の関数を宣言
        gf = gaussian(mu, sigma)

        # Eステップ: 事前分布 l(x)と尤度関数(提案分布) piをかけて、事後分布(期待値)を求める
        post_pro = Expectatoin_Step(X, pi, gf)

        # Mステップ: Q関数を最大化するパラメタ mu, sigma, pi を求める
        mu, sigma, pi = Maximization_Step(X, post_pro)

        # 分散が0になったら、乱数で置き換える
        if 0 in sigma:
            sigma = np.abs(np.random.randn(K))
            continue

        # 最適化された変数で、K個のガウシアンをプロットする
        tmp = []
        for i in range(K):
            im = pyplot.plot(seq, 1/K * gaussian(mu[i], sigma[i])(seq), linewidth=2.0, color=colors[i])
            tmp.append(im[0])
        ims.append(tmp)

        # Q関数の計算
        Q_new = calc_Q(X, mu, sigma, pi, post_pro)
        delta = np.abs(Q_new - Q)
        Q = Q_new
        print(index,delta,epsilon, sigma)
        index += 1

    # gifとして保存
    ani = animation.ArtistAnimation(fig, ims, interval=300)
    pyplot.ylim(0, 1)
    ani.save('EM_Algorizm.gif', writer='pillow')
    pyplot.show()

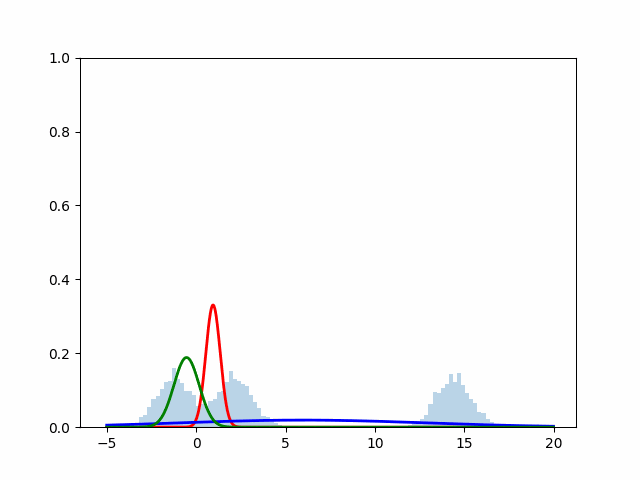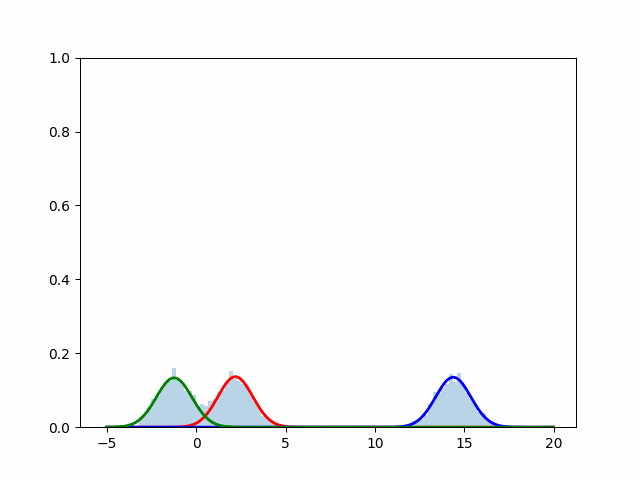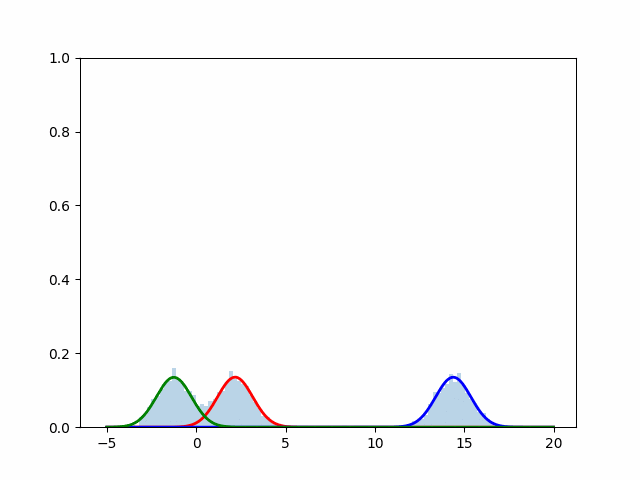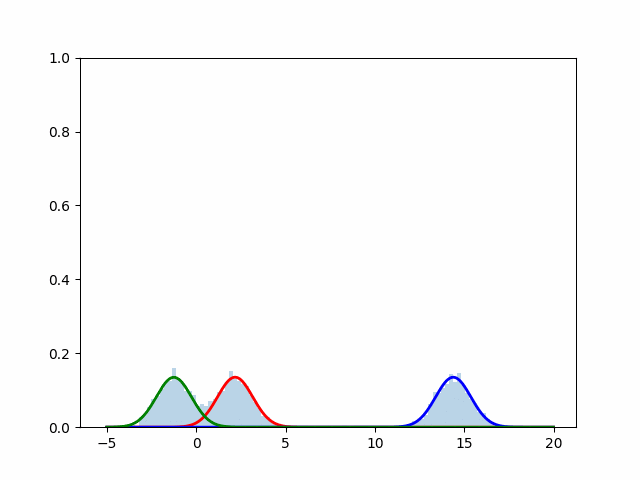
実行結果

scikit-learnを使用した場合

一次元で二つの混合ガウス分布モデルでの推定

EM_Algorithm.py

import numpy as np
from scipy.stats import norm
from sklearn.mixture import GaussianMixture

# Generate artificial data with two Gaussian components
np.random.seed(0)
data = np.concatenate([np.random.normal(0, 1, 50), np.random.normal(5, 1, 50)])

# Fit a Gaussian mixture model using the EM algorithm
model = GaussianMixture(n_components=2)
model.fit(data.reshape(-1, 1))

# Print the estimated means and covariance matrices
print("Means:", model.means_)
print("Covariances:", model.covariances_)

まとめ

今回は、EMアルゴリズムについて、紹介した。