この記事について
Neo4jを使ったグラフアルゴリズムの実装を紹介してみようという計画「グラフアルゴリズム入門 - javaとNeo4jで学ぶ -」の一部です(どこまで続くか・・・)
サンプルコードはこちらにおいた。
グラフの探索
グラフを探索するとは、ある頂点(ノード、Neo4jではNode)から辺(エッジ、Neo4jではRelationship、今後、関連と呼ぶことにする)を順々にたどって別の目標(ゴール)とするノードに到達することである。グラフ探索として、一番基本的なアルゴリズムとして、幅優先探索と深さ優先探索がある。幅優先探索とは、あるノードからスタートするとき、その隣接するノードを優先することを繰り返して、ゴールに到達しようとするアルゴリズムである(最初のレイヤのノードを順に探索する)。それに対し、深さ優先探索とは、隣接するノードから、さらに隣接するノードを優先することを繰り返してゴールに到達しようとするアルゴリズムである(なければ次のレイヤのノードを探索する)。
幅優先探索
次に幅優先探索のサンプルプログラムを示す。これは、Neo4jのプロシージャとして書かれている。プロシージャの作り方については、この記事に解説した。入力としてはノードのidをもらい、出力には、到達したノードと、そのノードに至るパスを入れている。到達したノードは探索で訪れた順番ですべて出力される。
幅優先探索はキューを使うことによってシンプルに書くことができる。到達したかどうかは配列visitedで管理する。もし到達済みでないのなら、到達したノード(Nodeオブジェクトc_nd)に隣接するノードを求め(getRelationshipsで関連を求め、getOtherNodeで隣接するノードを求めている)、キューに入れる。そして次にキューからノードを取り出し同じことを繰り返す。
ノードに至るパスを求めるためには、一般的には一つ手前のノード(親ノード)を記録していくことが多いが、Neo4jの場合は一つ手前の関連を記録していくのが便利である。それがノードと一つ手前の関連の対応を記録するマップのparentである。getPath()は、この関連の記録を辿って、入力ノードから到達したノードまでのパスを求める関数である。
// sample6_1: BFS
@Procedure(value = "example.sample6_1")
@Description("sample6_1: BFS")
public Stream<Output> sample6_1( @Name("id") Long id )
{
// start node
Node start_nd = db.getNodeById(id);
// map for keeping Node and parent relationship
Map<Node, Relationship> parent = new HashMap<>();
// to avoid coming back to start node
parent.put(start_nd, null);
// array for checking whether the node was visited
List<Node> visited = new ArrayList<>();
// queue
Queue<Node> queue = new ArrayDeque<>();
// current node
Node c_nd = start_nd;
// list for result
List<Output> o_l = new ArrayList<>();
// end if queue is empty
while(c_nd != null) {
Iterable<Relationship> rels = c_nd.getRelationships();
if(!(visited.contains(c_nd))) {
for(Relationship rel: rels){
// if not visited add next node
Node n_nd = rel.getOtherNode(c_nd);
if(!parent.containsKey(n_nd)) {
queue.add(n_nd);
parent.put(n_nd, rel);
}
}
visited.add(c_nd);
}
Output o = new Output();
o.node = c_nd;
// get path from start_nd to o
o.path = getPath(start_nd, c_nd, parent);
o_l.add(o);
// get next node from queue
c_nd = queue.poll();
}
return o_l.stream();
}
// construct path from parent relationships
public Path getPath(Node frm_nd, Node to_nd, Map<Node, Relationship> parent) {
PathImpl.Builder builder = new PathImpl.Builder(frm_nd);
// queue
Deque<Relationship> queue = new ArrayDeque<>();
Node tmp_nd = to_nd;
while(!tmp_nd.equals(frm_nd)){
Relationship r = parent.get(tmp_nd);
queue.push(r);
tmp_nd = r.getOtherNode(tmp_nd);
}
Relationship tmp_r = queue.poll();
while(tmp_r != null){
builder = builder.push(tmp_r);
tmp_r = queue.poll();
};
return builder.build();
}
// result class of sample
public class Output{
public Node node;
public Path path;
}
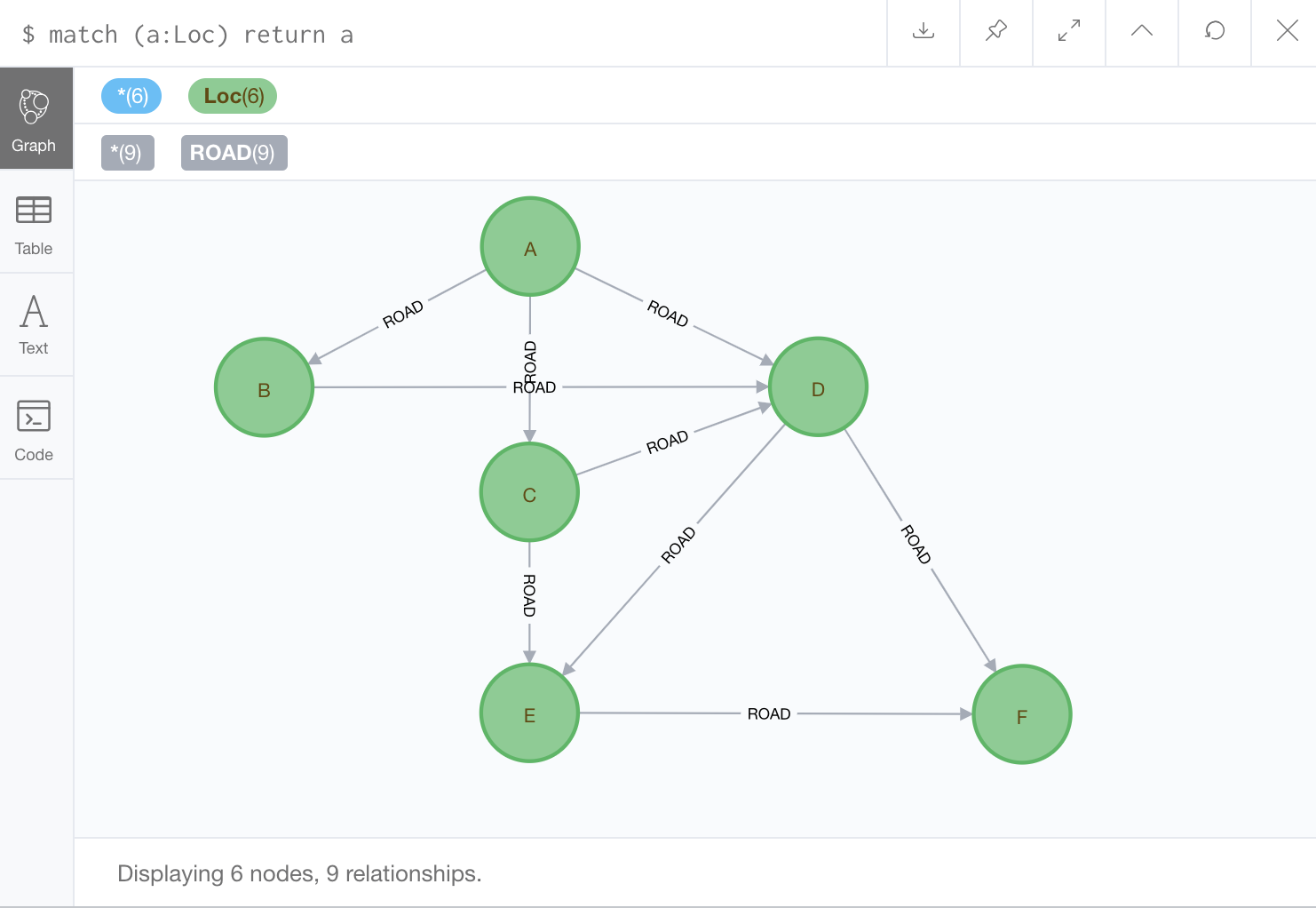
このプログラムの実行例を示す。次のサンプルを利用する。これはNeo4j Browserの画面である。関連の向きがあるが、プログラム上は無向グラフとして処理している。
上記のプログラムをプロシージャとしてNeo4jに取り込み、A(idが0)からスタートして実行すると以下の結果が得られる。確かに幅優先順にノードが取得されていることがわかる。
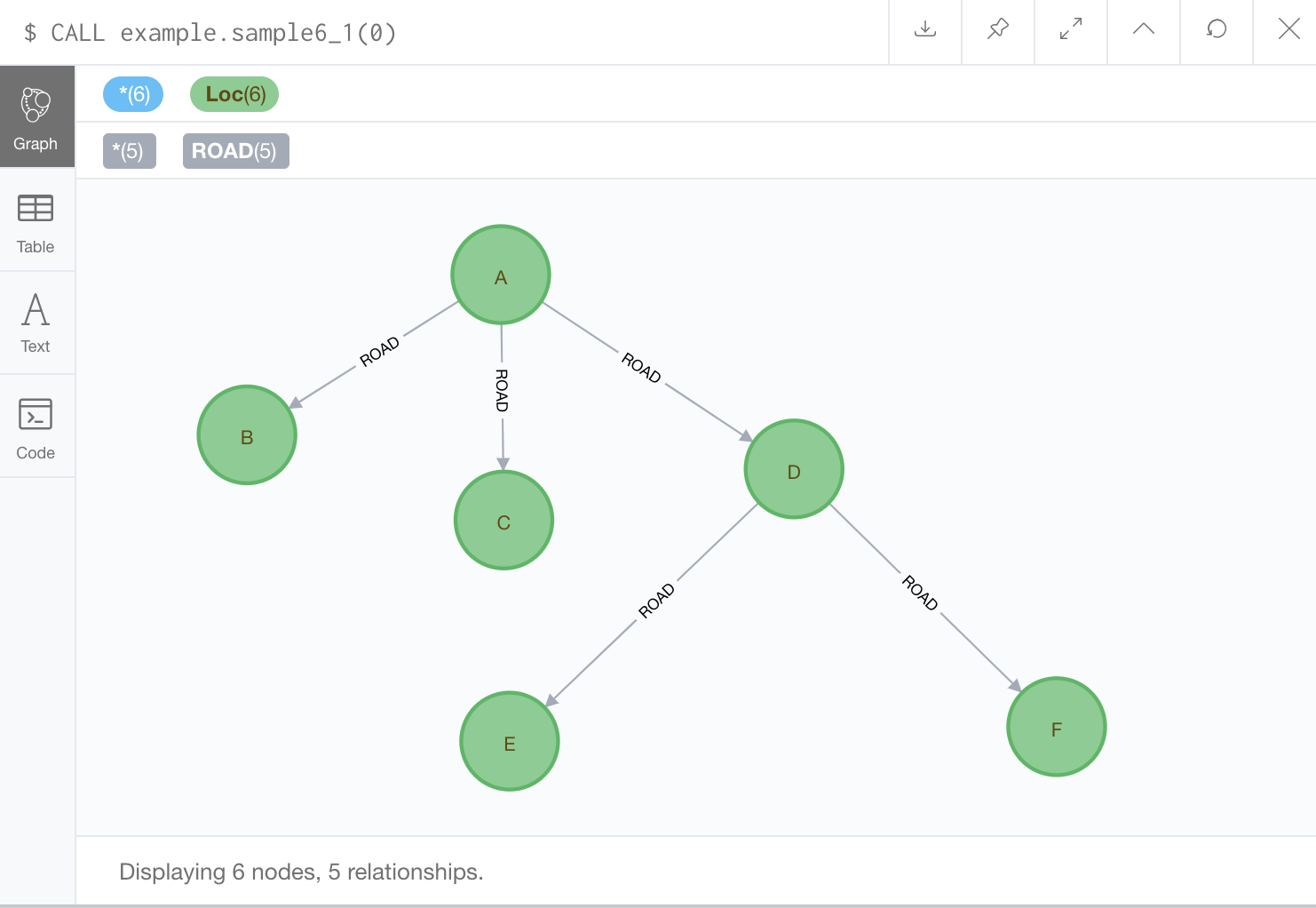
これは結果として得られたすべてのパスをまとめて表示している。これはツリー(木)となっているが、幅優先探索の結果のパスを集めると必ずツリーとなる。これは、幅優先探索木と呼ばれるものである。このように容易に可視化して確認できるのは、Neo4jを利用する大きなメリットである。ただし、一点、注意点があり、下の探索結果の表示では、Neo4jブラウザの設定の「Connect result nodes」をOFFにしている。このオプションは、Neo4j Browser上でノードが探索されたときに、それらのノード間にある関連をすべて表示するというもので、デフォルトはONである。そのほうが容易にグラフのつながりが見えるからであろう。上のサンプルの図ではONで表示している(OFFにすると、match (a) return aはノードしか返さないので、孤立したノードのみが表示される)。