Neo4jでグラフアルゴリズム：双方向ダイクストラ探索

この記事について

Neo4jを使ったグラフアルゴリズムの実装を紹介してみようという計画「グラフアルゴリズム入門 - javaとNeo4jで学ぶ -」の一部です（どこまで続くか・・・）

サンプルコードはこちらにおいた。

双方向ダイクストラ探索

秋葉さんのスライド：大規模グラフアルゴリズムの最先端のP.16近辺に少し記述がある。双方向ダイクストラ探索は、与えられた2点の最短経路を求めるアルゴリズムであるが、その2点の両側からダイクストラ探索を実行し、ぶつかったら最短距離の候補として記憶する。さらに「よりよい（短い）経路が見つけられない」ことが判定できたら、解が見つかったことになる。双方向ダイクストラ探索は、最悪ケースではダイクストラ探索と同等の計算量となるが、データには依存するものの探索範囲を狭める効果がある。下図は上記のスライドから引用した図であり、双方向ダイクストラ探索のイメージをわかりやすく示している。

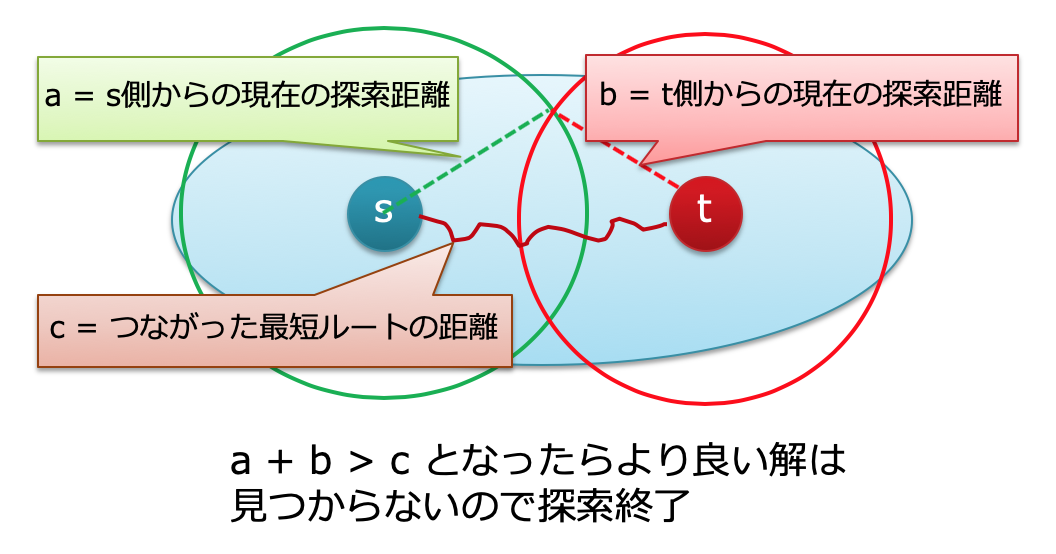
「よりよい（短い）経路が見つけられない」の判定には、三角不等式を使う。候補の最短距離が、（スタート側から探索して到達した距離＋エンド側から探索して到達した距離）を下回れば、その候補よりもさらに短い経路を発見することはないから終了してよい。下図にイメージを示す。

Neo4jによる実装

まず、ノードの隣を展開して、プライオリティキューに登録していく部分は、スタート側、エンド側の双方で共通に使われるので関数として切り出しておこう。ここはダイクストラ法で用いたものと全く同じ処理である。

	// get adjacent nodes and add them to queue
	public void getAdjacentNodes(NodeInfo cur_ni, PriorityQueue<NodeInfo> pq, Map<Node, NodeInfo> nodes, Map<Node, Relationship> parent) {
		// Property for cost: type must be double
		String cost_property = "cost";
		Iterable<Relationship> rels = cur_ni.nd.getRelationships();
		for (Relationship rel : rels) {
			// get adjacent nodes and their costs
			Node o_nd = rel.getOtherNode(cur_ni.nd);
			double cost_rel = (double) rel.getProperty(cost_property);
			// check whether the node was found
			NodeInfo next_ni = nodes.get(o_nd);
			// not found -> 1st appearance of the node, add it to map
			if (next_ni == null) {
				next_ni = new NodeInfo(o_nd, cur_ni.cost + cost_rel);
				pq.add(next_ni);
				nodes.put(o_nd, next_ni);
				parent.put(o_nd, rel);
			}
			// found but cost is't fixed and has lower cost -> overwrite cost
			else if (next_ni.done == false) {
				if (next_ni.cost > cur_ni.cost + cost_rel) {
					next_ni.cost = cur_ni.cost + cost_rel;
					parent.put(o_nd, rel);
				}
			}
			// found and cost was fixed -> do nothing
		}
	}

スタート側とエンド側について、普通のダイクストラの場合と同様に、それぞれプライオリティキューやマップを用意する必要がある。探索を進める方法であるが、ここでは、2つのキューの先頭のコストを比較してが小さい側を展開する。左右の探索範囲が同程度の大きさで少しずつ広がるイメージである。whileループを脱出する条件が異なっていて、それぞれ、以下のようになる。

• （経路を見つける前に）どちらかのプライオリティキューが空になってしまう場合は、つながる経路が存在しない場合なので、解なし
• 片側から探していって、（双方向の結果をあわせるまでもなく）目標とするノードに到達してしまう場合は、これは最短経路であるから、それをそのまま返せばよい
• 上で説明した三角不等式を満たす場合、これは双方向の結果をつなげたものが求める最短経路である。

片側のノードのコストが確定したタイミングで、もう反対側のキューに登録されている（つまり、暫定的にでもコストが求められている。このプログラムではnodes_f, nodes_tに登録さているかどうかを調べる）かどうかを調べ、もし登録されていて、全体のコストがこれまでより小さくなるならば、最小値を更新する。もし、仮に上記の反対側のコストが暫定的であっても、そのコストが確定するタイミングで反対側を調べに行くから、最終的には最適な値を求めることができる。

	// sample8_2: bidirectional djkstra
	@Procedure(value = "example.sample8_2")
	@Description("sample8_2: bidirectional djkstra")
	public Stream<Output> sample8_2(@Name("from_id") final Long from_id, @Name("to_id") final Long to_id) {
		final Node from_nd = db.getNodeById(from_id);
		final Node to_nd = db.getNodeById(to_id);
		// Priority Queue by cost property value
		final PriorityQueue<NodeInfo> pq_f = new PriorityQueue<>((n1, n2) -> Double.compare(n1.cost, n2.cost));
		final PriorityQueue<NodeInfo> pq_t = new PriorityQueue<>((n1, n2) -> Double.compare(n1.cost, n2.cost));
		// map for keeping node and cost
		final Map<Node, NodeInfo> nodes_f = new HashMap<>();
		final Map<Node, NodeInfo> nodes_t = new HashMap<>();
		// map for keeping Node and parent relationship
		final Map<Node, Relationship> parent_f = new HashMap<>();
		final Map<Node, Relationship> parent_t = new HashMap<>();
		
		// current node(info)
		NodeInfo cur_ni_f = new NodeInfo(from_nd, 0.0);
		pq_f.add(cur_ni_f);
		nodes_f.put(from_nd, cur_ni_f);
		NodeInfo cur_ni_t = new NodeInfo(to_nd, 0.0);
		pq_t.add(cur_ni_t);
		nodes_t.put(to_nd, cur_ni_t);

		// node that f-side path and t-side path meets
		NodeInfo min_ni_f = null;
		NodeInfo min_ni_t = null;

		// variables for checking to exit
		double total_cost = 100000; // total cost

		// Result
		final Output o = new Output();

		// Path finding
		while(true) {
			// if one queue is empty, no route exit
			if(cur_ni_f == null || cur_ni_t == null) {
				return new ArrayList<Output>().stream();
			}
			// exit when found to node in the from-side
			if(cur_ni_f.nd.equals(to_nd)) {
				o.path = getPath(from_nd, min_ni_f.nd, parent_f);
	    		o.cost = cur_ni_f.cost;
	    		break;
			}
			// exit when found from node in the to-side
			if(cur_ni_t.nd.equals(from_nd)) {
	    		o.path = reverse(getPath(to_nd, min_ni_t.nd, parent_t));
	    		o.cost = cur_ni_t.cost;
	    		break;			
			}
		    // exit when cannot find shorter path (triangle inequality)
			// (total cost) < (current f-side cost) + (current t-side cost)
	    	if(cur_ni_f.cost + cur_ni_t.cost > total_cost){
	    		final Path f_path = getPath(from_nd, min_ni_f.nd, parent_f);
	    		final Path t_path = getPath(to_nd, min_ni_t.nd, parent_t);
	    		o.path = cat(f_path, reverse(t_path));
	    		o.cost = total_cost;
	    		break;
			}
			// expand from-side
			if(pq_f.peek().cost <= pq_t.peek().cost){
				// top node of queue's cost is fixed
				cur_ni_f = pq_f.poll();
				cur_ni_f.done = true;
				// find the node in the other side
				final NodeInfo ni_t = nodes_t.get(cur_ni_f.nd);
				// the node is in the other side map and total_cost can be lower
				if(ni_t != null && total_cost > cur_ni_f.cost + ni_t.cost) {
					min_ni_f = cur_ni_f;
					min_ni_t = ni_t;
					total_cost = cur_ni_f.cost + ni_t.cost;					
				}
				// get adjacent nodes and add them to queue
				// Property for cost: type must be double
				getAdjacentNodes(cur_ni_f, pq_f, nodes_f, parent_f);
			}
			// expand to-side
			else{
				cur_ni_t = pq_t.poll();
				cur_ni_t.done = true;
				final NodeInfo ni_f = nodes_f.get(cur_ni_t.nd);	
				if(ni_f != null && total_cost > ni_f.cost + cur_ni_t.cost) {
					min_ni_f = ni_f;
					min_ni_t = cur_ni_t;
					total_cost = ni_f.cost + cur_ni_t.cost;	
				}		
				getAdjacentNodes(cur_ni_t, pq_t, nodes_t, parent_t);
			}			
		}
		// list for result
		final List<Output> o_l = new ArrayList<>();
		o_l.add(o);
		return o_l.stream();
	}

双方向のパスをまとめて一つのパスを作るために使った、パスを逆転する処理とくっつける処理については、以下のようになっている。

	// reverse Path
	public Path reverse(Path p) {
		PathImpl.Builder builder = new PathImpl.Builder(p.endNode());		
		for(Relationship r: p.reverseRelationships()) {
			builder = builder.push(r);
		}
		return builder.build();
	}
	// concatenate two Paths 
	public Path cat(Path p1, Path p2) {
		PathImpl.Builder builder = new PathImpl.Builder(p1.startNode());
		Iterable<Relationship> rels1 = p1.relationships();
		Iterable<Relationship> rels2 = p2.relationships();
		for(Relationship r: rels1) {
			builder = builder.push(r);
		}
		for(Relationship r: rels2) {
			builder = builder.push(r);
		}
		return builder.build();
	}