駅メモで最適化
今の駅メモのイベント。
「材料を集めて美味しいご飯を作るとポイント獲得」のところで、最適化ができそうでした。
ルール概要
TODO:画像を貼る
- ゲームを進めると秋っぽい食材が手に入る。
- 薪、栗、皿、魚、きのこ、ぶどう、調味料、あけび、まつたけ
- 9種類の材料の組み合わせで作る5種類のメニューがある
- 焼き栗=薪+栗、魚の塩焼き = 薪+栗+魚、etc...
- メニューを1つ作成すると、材料が1つずつ消費されて、当該メニューに割り当てられたポイントが獲得できる
- 焼き栗は30ポイント、魚の塩焼き120ポイント、etc...
最適化の定式化
変数を以下のように定義して、
\begin{align}
x_i &= \text{(メニュー$i$を作る個数)}, \\
y_{ij} &= \text{(メニュー$i$が材料$j$を使うなら1)}, \\
z_{j} &= \text{(材料$j$の個数)}, \\
P_{i} &= \text{(メニュー$i$を1つ作る時のポイント)},
\end{align}
以下のように定式化できます。
\begin{align}
\max & \sum\limits_{i=1..5} P_i x_i, \\
\mathrm{s.t} \ \ x_i &>=0, \\
\sum\limits_{i=1..5} x_i y_{ij} &<= z_j \ (j = 1..9)
\end{align}
実行環境
ColaboratoryとPulpで最適化します。↓を読みましょう。
https://www.y-shinno.com/pulp-intro/
よくわかりました。
実装
TeXをいい感じに書くよりも、実装する方が簡単です。
!pip install pulp
import pulp
# 問題の定義
problem = pulp.LpProblem(name="EKIMEMO_2022_Autumn", sense=pulp.LpMaximize)
# 変数の定義
A = pulp.LpVariable(name = "Yakiguri", lowBound = 0, cat="Integer")
B = pulp.LpVariable(name = "Shioyaki", lowBound = 0, cat="Integer")
C = pulp.LpVariable(name = "Kinoko-Jiru", lowBound = 0, cat="Integer")
D = pulp.LpVariable(name = "Moriawase", lowBound = 0, cat="Integer")
E = pulp.LpVariable(name = "Matsutake-Gohan", lowBound = 0, cat="Integer")
# 目的関数(得られるスコア)
problem += 30 * A + 120 * B + 200 * C + 500 * D + 700 * E
# 制約条件の定義
problem += A+B+C +E <= maki ## maki: 材料「薪」の個数
problem += A+B +D <= kuri ## kuri: 材料「栗」の個数
problem += C +E <= sara ## sara: (以下同様)
problem += D <= budou
problem += B +D <= sakana
problem += E <= chomiryo
problem += C +E <= kinoko
problem += D <= akebi
problem += E <= matsutake
# 解く
status = problem.solve()
print(pulp.LpStatus[status])
# 結果表示
print("Result")
print("Yakiguri:", A.value())
print("Shioyaki:", B.value())
print("Kinoko-Jiru:", C.value())
print("Moriawase:", D.value())
print("Matsutake-Gohan:", E.value())
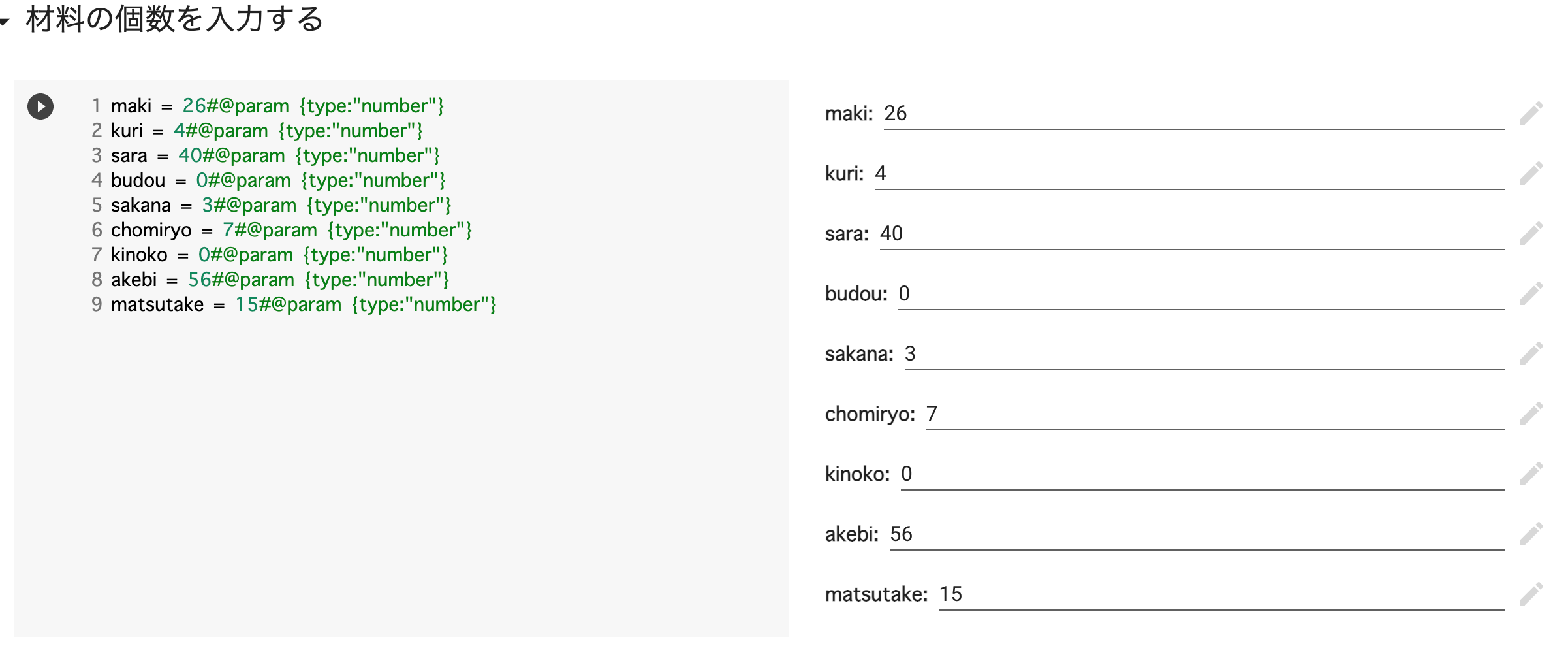
UI
https://qiita.com/john-rocky/items/e5802cdd15dc2e34cb84
これを参考に、今持っている材料の個数を入力するためのフォームを作りました。便利ですね。
解く
解きましょう

解けました。材料足りないので、解がつまらんです。
今後の取り組み
- Webアプリにする
- pulpの目的関数や制約を、for文で書く
- ゲームを頑張って材料を集める