はじめに
SpaceXでは、完全再使用に向けた宇宙輸送システムStarshipの開発を行っており、既に10回のフライトテストを実行し、驚異的なスピードで成果を上げています。
SpaceXでは従来的なウォーターホール開発ではなく、アジャイル開発を導入し、最初から100%を目指さず、6~7割の機能で検証し、とにかく継続的な改善、開発のサイクルをスピーディに回して高頻度でテストすることでその精度を高めていっています。
その裏付けとして打ち上げ10回目ですでに第一段ロケット"Super Heavy"ならびに第2段の宇宙船"Starship"の大気圏再突入ならびに制御された着水(Splashdown)を成し遂げ、ミッションのフルコンプリートを達成しています。
さらに脅威的なのが、Super Heavyの帰還システムであるMechazila(通称お箸キャッチ)です。
Super Heavyの構造重量の削減ならび迅速な再利用のための運用性を考慮し、タワーでキャッチして回収するという前代未聞な大胆な構成をとったそうです。
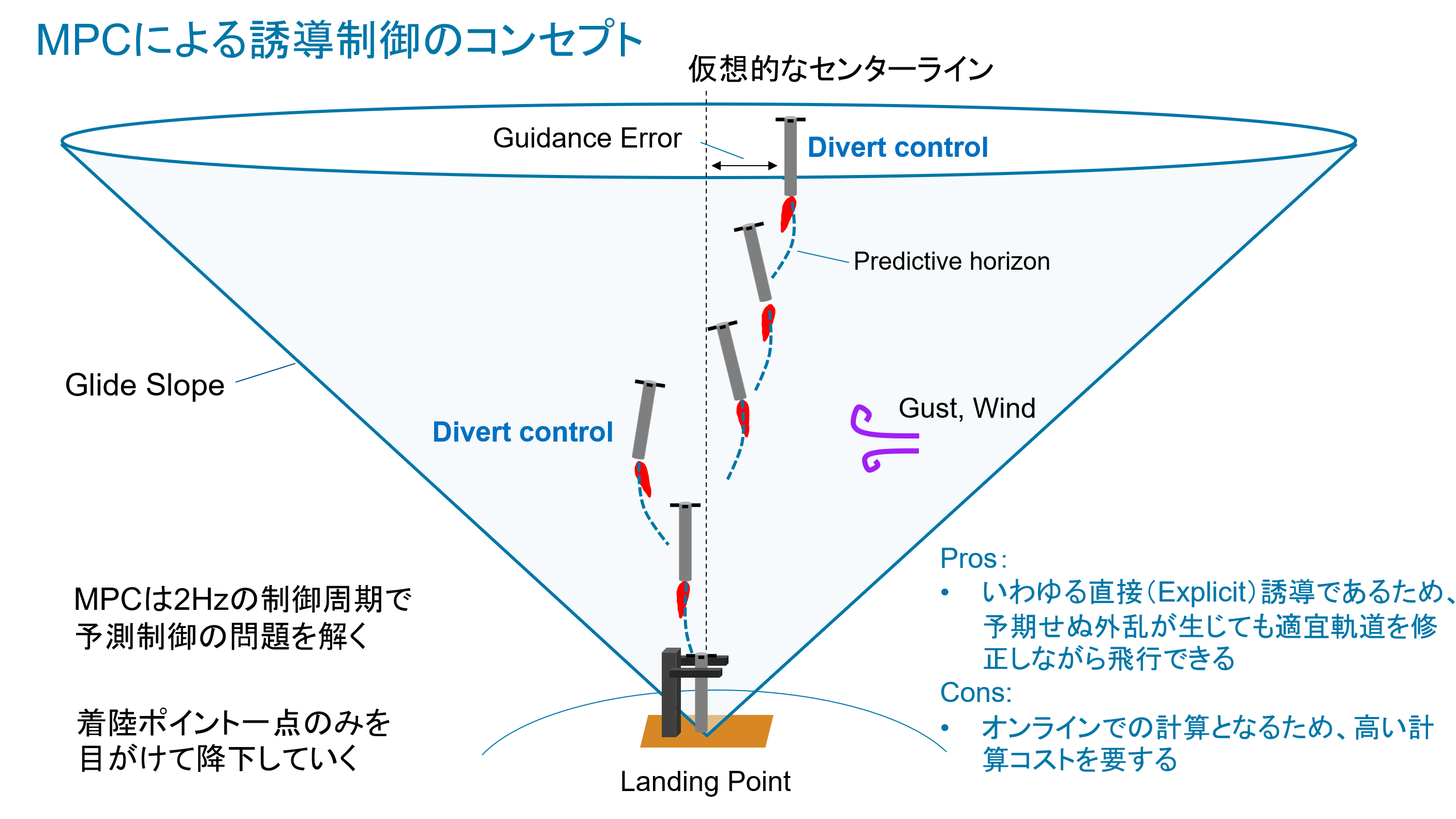
こうなるとロケットをタワーまでゆっくり近づけながら、お箸でキャッチするタイミングを合わせるという、非常に精密な誘導制御とタイミングの同期が必要となってくると考えられるため、かなり難易度の高いシステムといえると思います。
本記事では、前回からの記事の進展として、このお箸キャッチをシミュレーションでトライしてみたいと思います。
誘導制御
今回も前回の記事に続き、ロケットの誘導制御には非線形MPCを使っていきたいと思います。
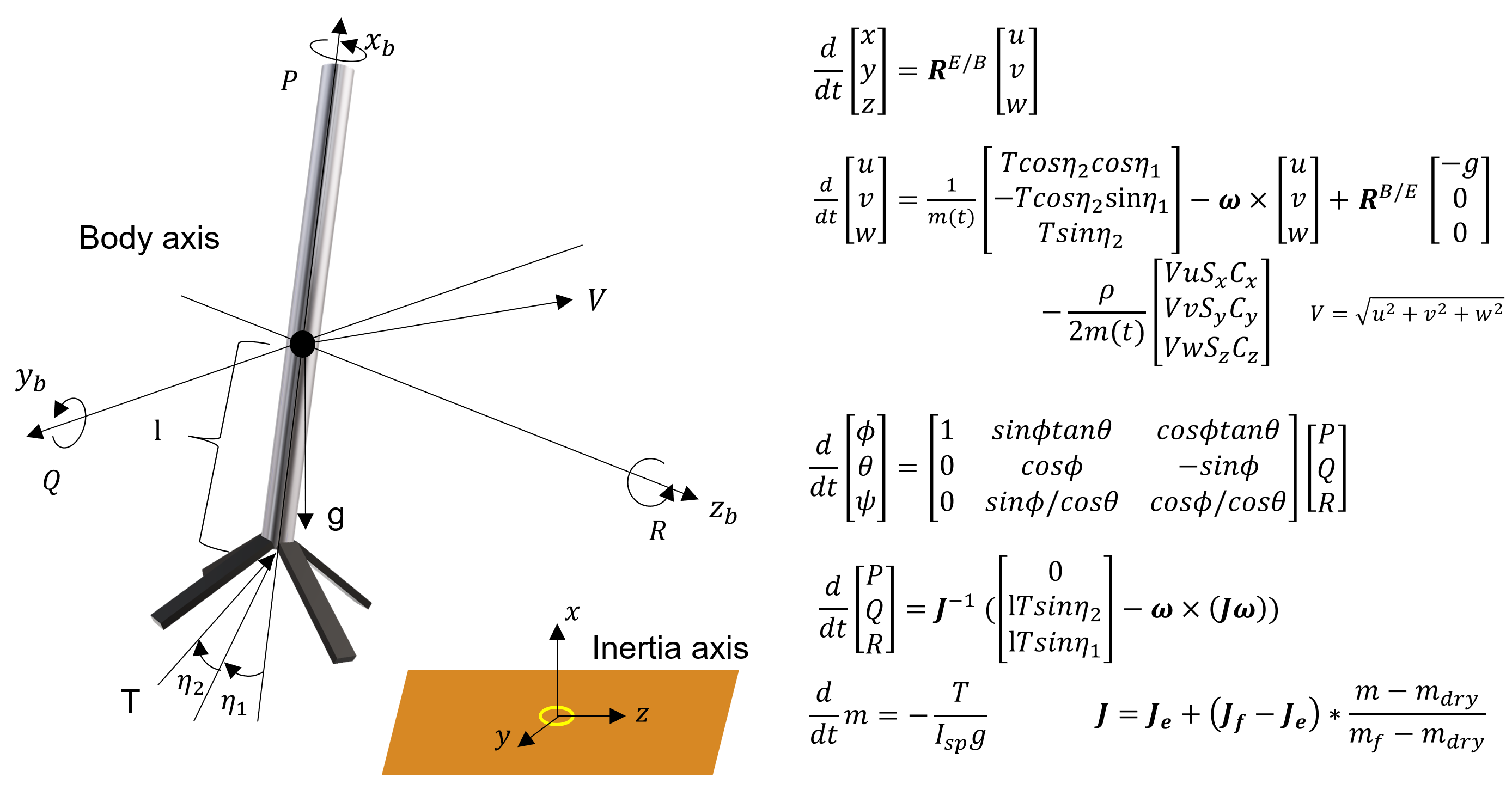
MPCの非線形な予測モデルとして、以下を定義します。
なお、予測モデルの定式化に当たっては計算の複雑化を避けるために以下を仮定します。
- 重心位置の変動は無視する
- 空力中心と重心は一致する
- 慣性特性は燃料満載時と乾燥時の間で線形に変化する
予測モデルの生成にはMATLABの数式処理ツールであるSymbolic Math Toolboxを使用します。
Deriving 6DoF State Equation of Lander Vehicle Model
% States
syms xe ye ze u v w phi theta psi p q r m
x1 = [xe;ye;ze];
x2 = [u;v;w];
x3 = [phi;theta;psi];
x4 = [p;q;r];
states = [x1;x2;x3;x4;m];
V = sqrt(u^2+v^2+w^2);
% Inputs
syms T ita1 ita2
inputs = [T;ita1;ita2];
% Parameters
syms s_L s_radius s_g s_Sx s_Sy s_Sz s_Cd s_rho s_Isp s_MainThrust
% Inertia matrix
I = I_e + (I_f-I_e)*((m-dry_mass)/(mass-dry_mass));
% Additional input parameters for NMPC
syms Q Qn R;
% Rotation Matrix
% Body to Inertia
Reb = [cos(psi)*cos(theta) cos(psi)*sin(theta)*sin(phi)-sin(psi)*cos(phi) cos(psi)*sin(theta)*cos(phi)+sin(psi)*sin(phi);
sin(psi)*cos(theta) sin(psi)*sin(theta)*sin(phi)+cos(psi)*cos(phi) sin(psi)*sin(theta)*cos(phi)-cos(psi)*sin(phi);
-sin(theta) cos(theta)*sin(phi) cos(theta)*cos(phi)];
% Inertia to Body
Rbe = [cos(psi)*cos(theta) sin(psi)*cos(theta) -sin(theta);
cos(psi)*sin(theta)*sin(phi)-sin(psi)*cos(phi) sin(psi)*sin(theta)*sin(phi)+cos(psi)*cos(phi) cos(theta)*sin(phi);
cos(psi)*sin(theta)*cos(phi)+sin(psi)*sin(phi) sin(psi)*sin(theta)*cos(phi)-cos(psi)*sin(phi) cos(theta)*cos(phi)];
% Angular velocity matrix
R_ang = [1 sin(phi)*tan(theta) cos(phi)*tan(theta);
0 cos(phi) -sin(phi);
0 sin(phi)/cos(theta) cos(phi)/cos(theta)];
% State Function
f = [Reb*x2;
1/m*([s_MainThrust*T*cos(ita2)*cos(ita1) -s_MainThrust*T*cos(ita2)*sin(ita1) s_MainThrust*T*sin(ita2)]')-cross(x4,x2)+Rbe*[-s_g 0 0]'-s_rho/(2*m)*[V*u*s_Sx*s_Cd V*v*s_Sy*s_Cd V*w*s_Sz*s_Cd]';
R_ang*x4;
inv(I)*(0.5*s_L*[0 s_MainThrust*T*sin(ita2) s_MainThrust*T*sin(ita1) ]'-cross(x4,I*x4));
-s_MainThrust*T/(s_Isp*s_g)];
f = subs(f,[s_L s_radius s_g s_Cd s_Sx s_Sy s_Sz s_rho s_Isp s_MainThrust],[L radius g Cd Sx Sy Sz rho Isp Main_Thrust]);
f = simplify(f)
% Generate jacobian
A = jacobian(f,states);
B = jacobian(f,inputs);
% Generate matlab function code
matlabFunction(f,'File','./source/landerStateFcn','Vars',{states,inputs,Q,Qn,R});
matlabFunction(A,B,'File','./source/landerStateJacobianFcn','Vars',{states,inputs,Q,Qn,R});
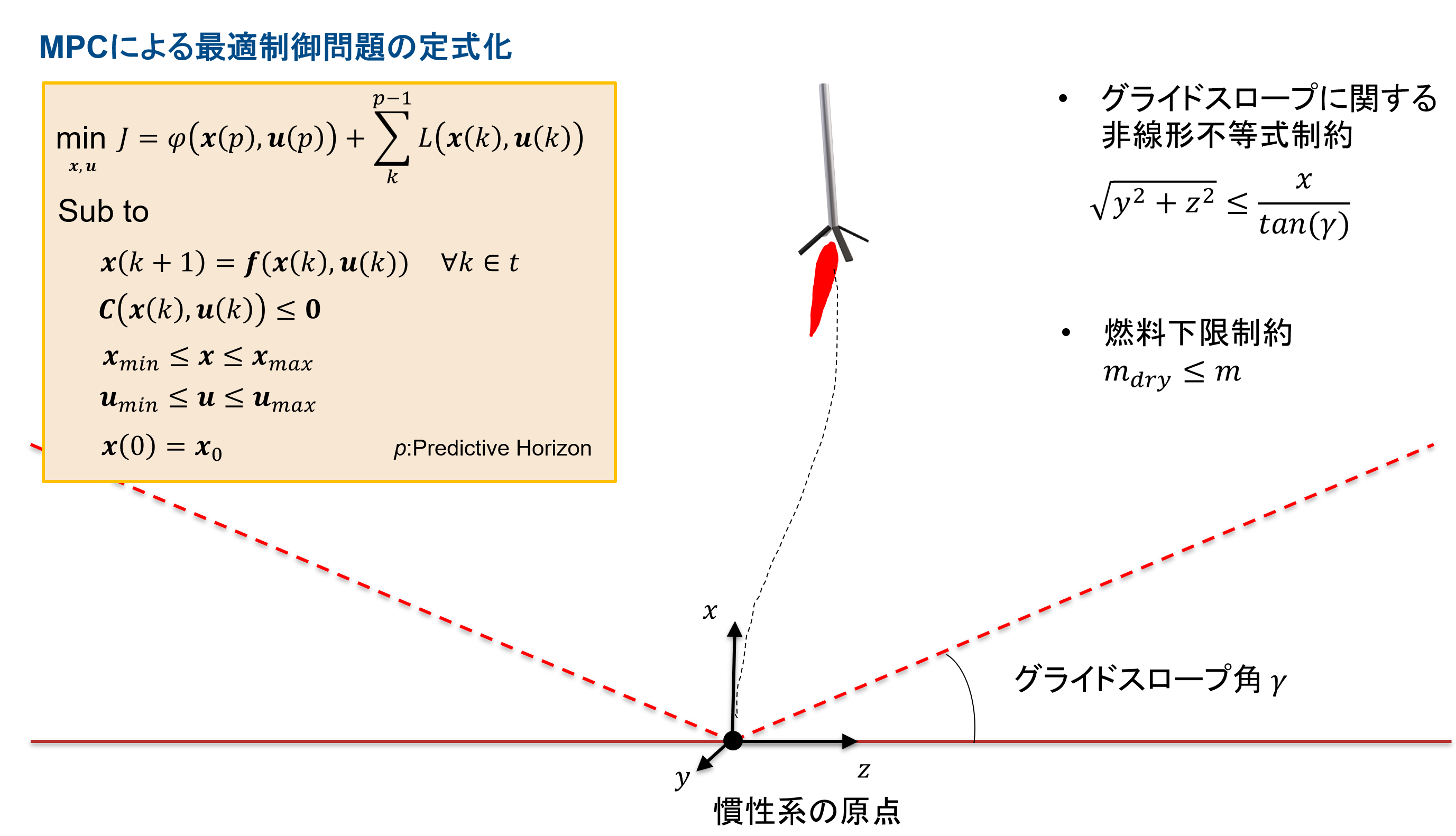
上記の予測モデルに対し、MPCを用いた最適制御問題を下図のように設定します。
ここで評価関数の中身としては、ステージコストおよび終端コストから構成し、各状態量に対して着陸時のあるべき規範量(一定値)との偏差として定義することにします。このように構成することで、有限な将来に亘る軌道を計画しつつ、規範状態への追従制御を同時に行います。
function J = landerCostFunction(X,U,e,data,Q,Qn,R)
% X:states
% U:inputs
% e:slack variable
% data:structured parameters
% Q,Qn,R:additional parameters (weights)
% Custom Cost Function
p = data.PredictionHorizon;
ref = data.References;
states = X(2:p+1,:);
err = states - ref;
% Scaling
m_ini = 500e3;
scaleFactor_X = [100 100 100 10 10 10 10*pi/180 10*pi/180 10*pi/180 10*pi/180 10*pi/180 10*pi/180 m_ini];
scaleFactor_U = [1 10*pi/180 10*pi/180];
err = bsxfun(@rdivide,err,scaleFactor_X);
U = bsxfun(@rdivide,U,scaleFactor_U);
J = 0;
for i = 1:p
if i < p
% Stage cost
J = J + 0.5*(err(i,:)*Q*err(i,:)' + U(i,:)*R*U(i,:)');
else
% Terminal cost
J = J + 0.5*(err(i,:)*Qn*err(i,:)');
end
end
% Add slack variable
J = J + 1e2*e^2;
end
以上で作成するMPCを用いて、以下のようなコンセプトに基づき、着陸のための誘導制御を行います。
シミュレーションモデル
シミュレーションモデルにおいて、ロケットのプラントモデルはMATLABの物理モデリングツールであるSimspace Multibodyで組みます。詳細については、前回の記事にて解説しておりますので興味のある方はご覧ください。
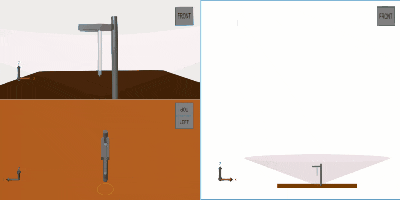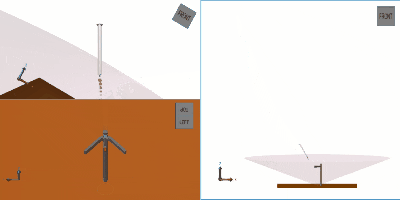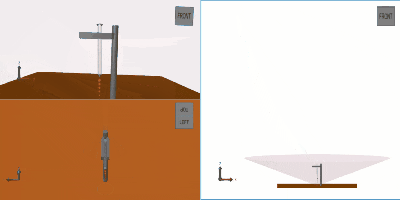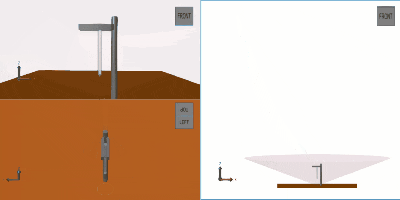
なお、前回からの相違点として、キャッチするためのタワーならびにアーム機構のモデルを加えています。
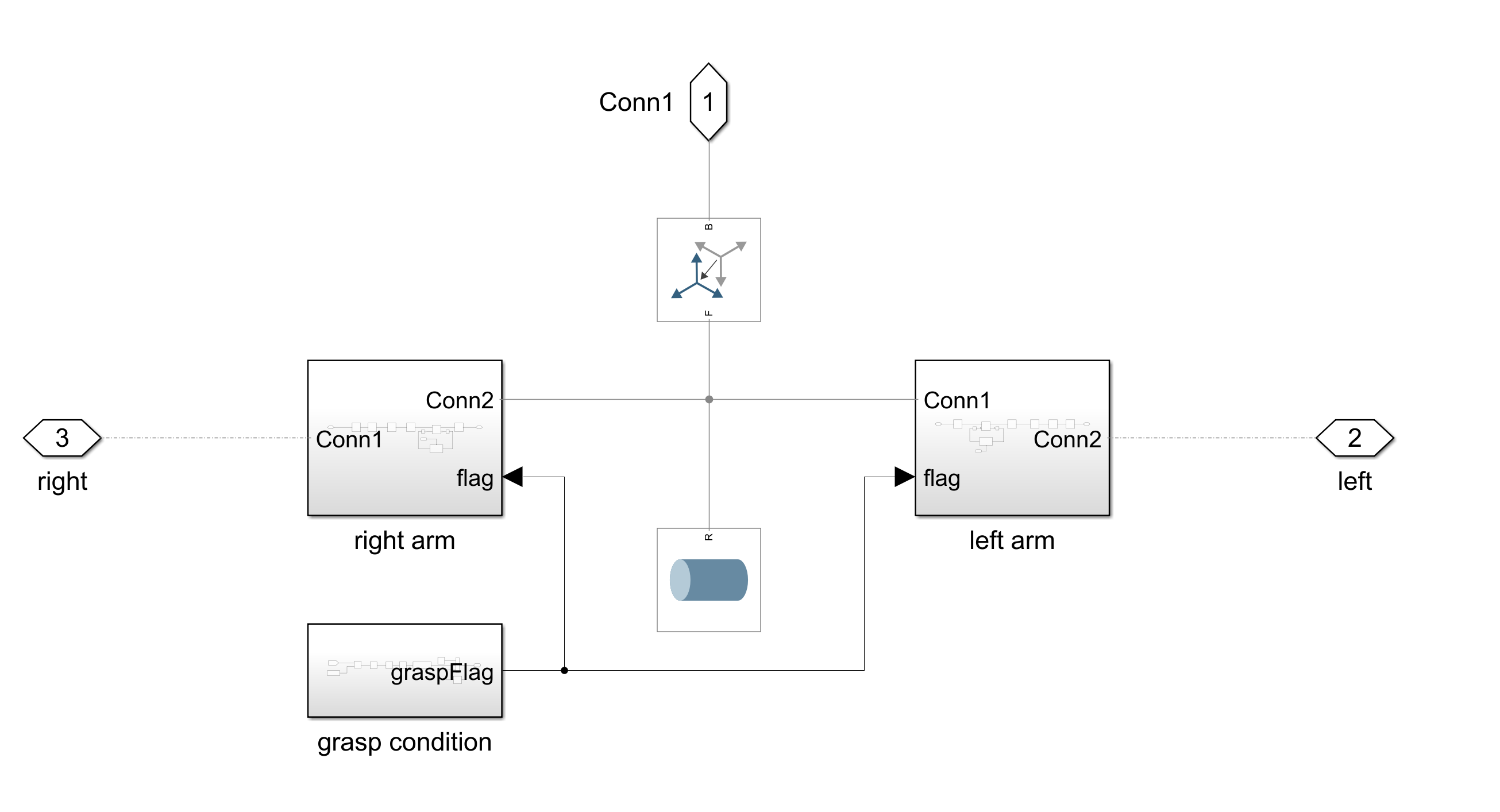
下図はタワーおよびアーム機構部のモデルです。
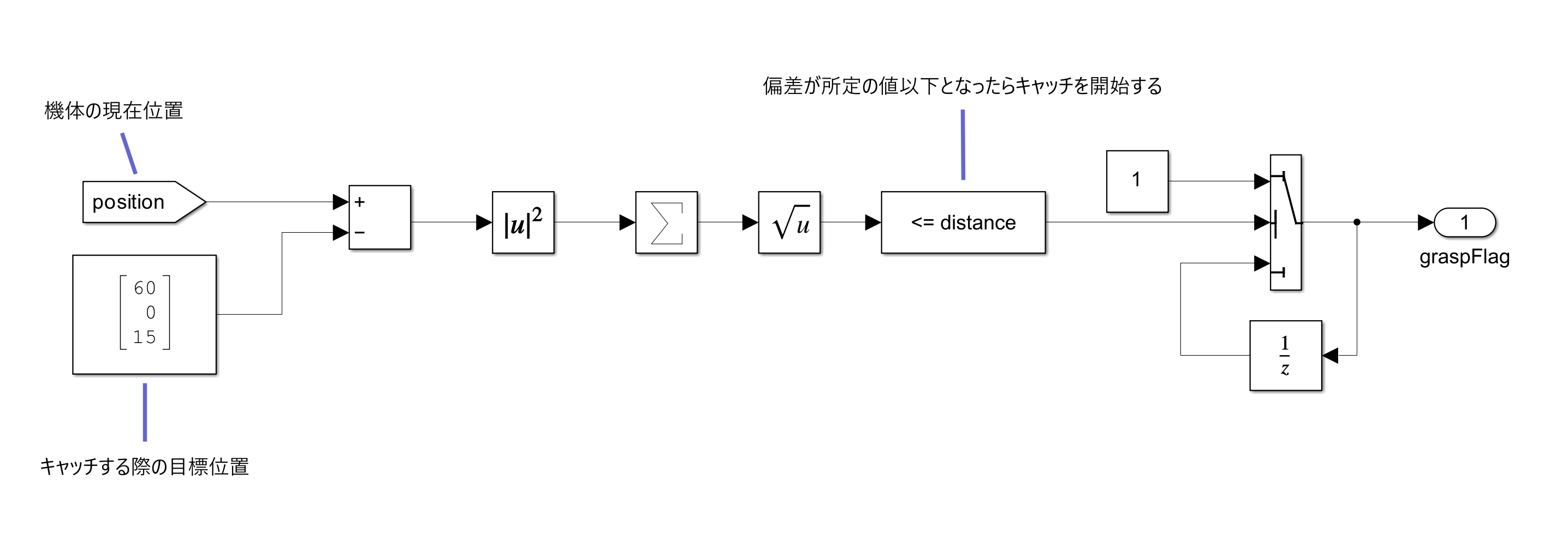
左右のアームは連動して駆動するものとして、判定条件(grasp condtion)に基づき、機体がタワーまで一定距離に近づいてきたら各アームの角度をキャッチ時の角度まで駆動させるとします。
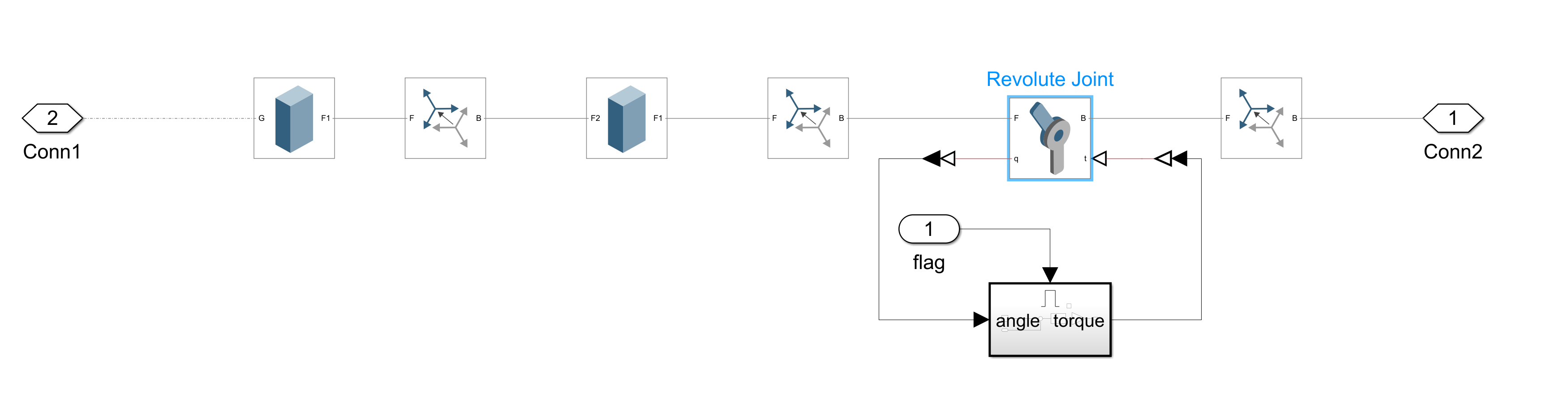
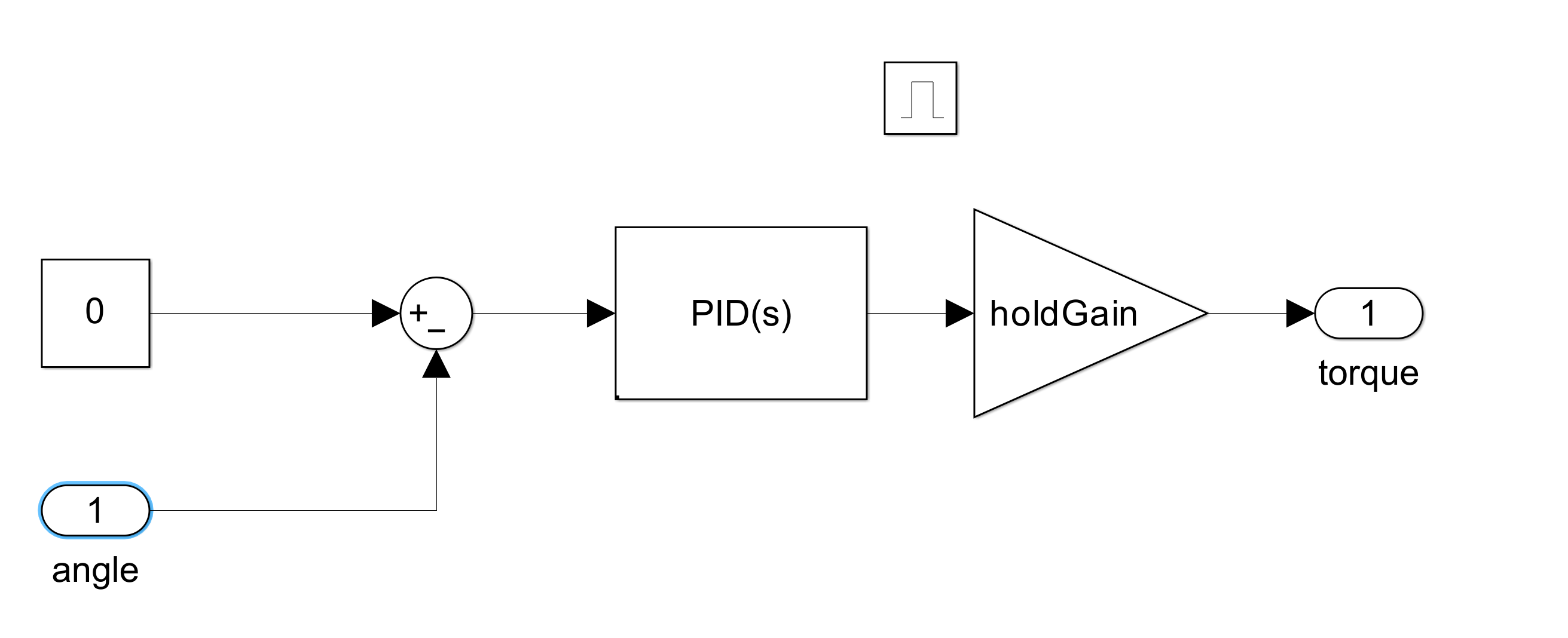
下図はアーム機構部のモデルであり、Revolute Jointブロックによって1軸回転の自由度を定義し、その駆動トルクをPIDによってフィードバック制御します。
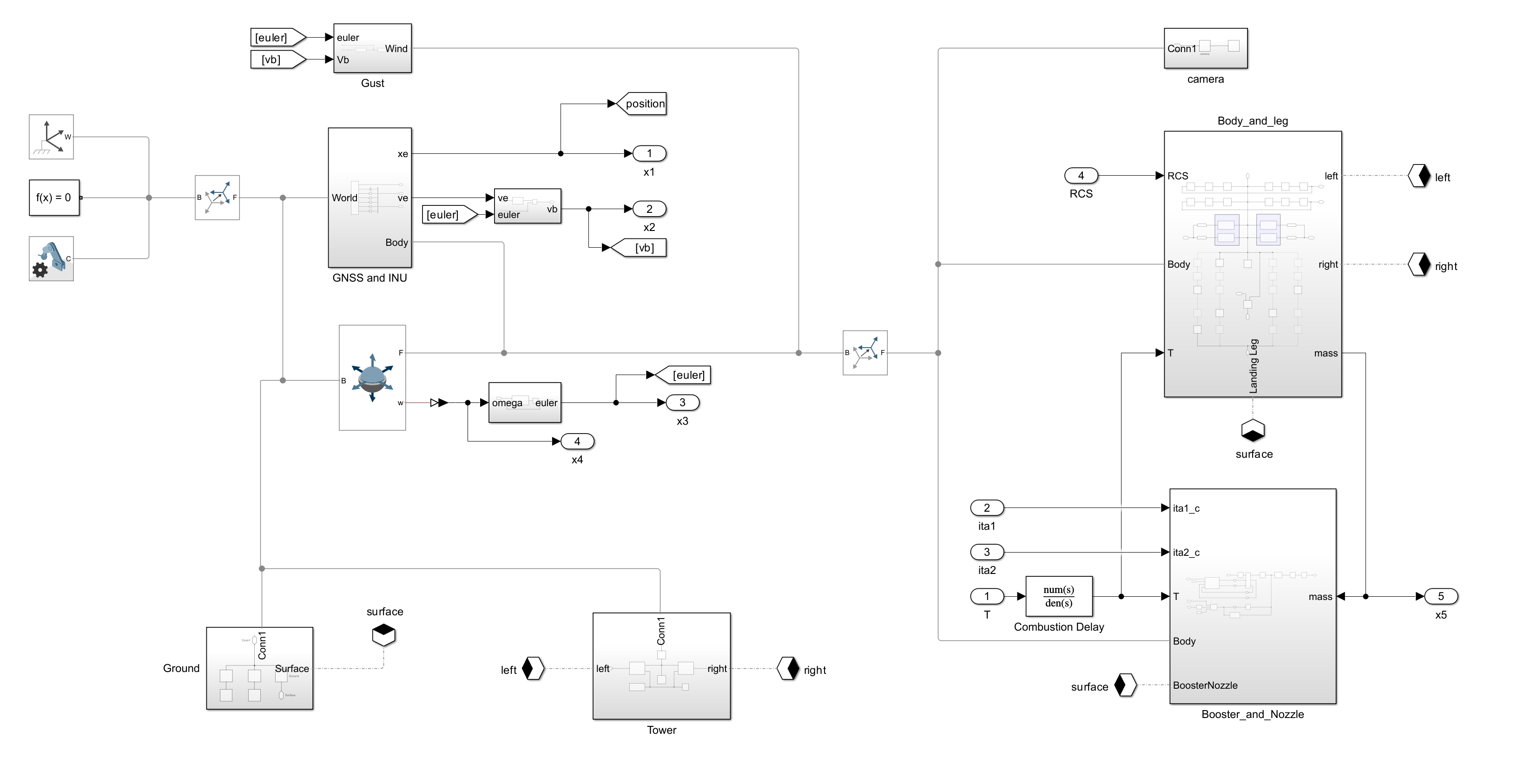
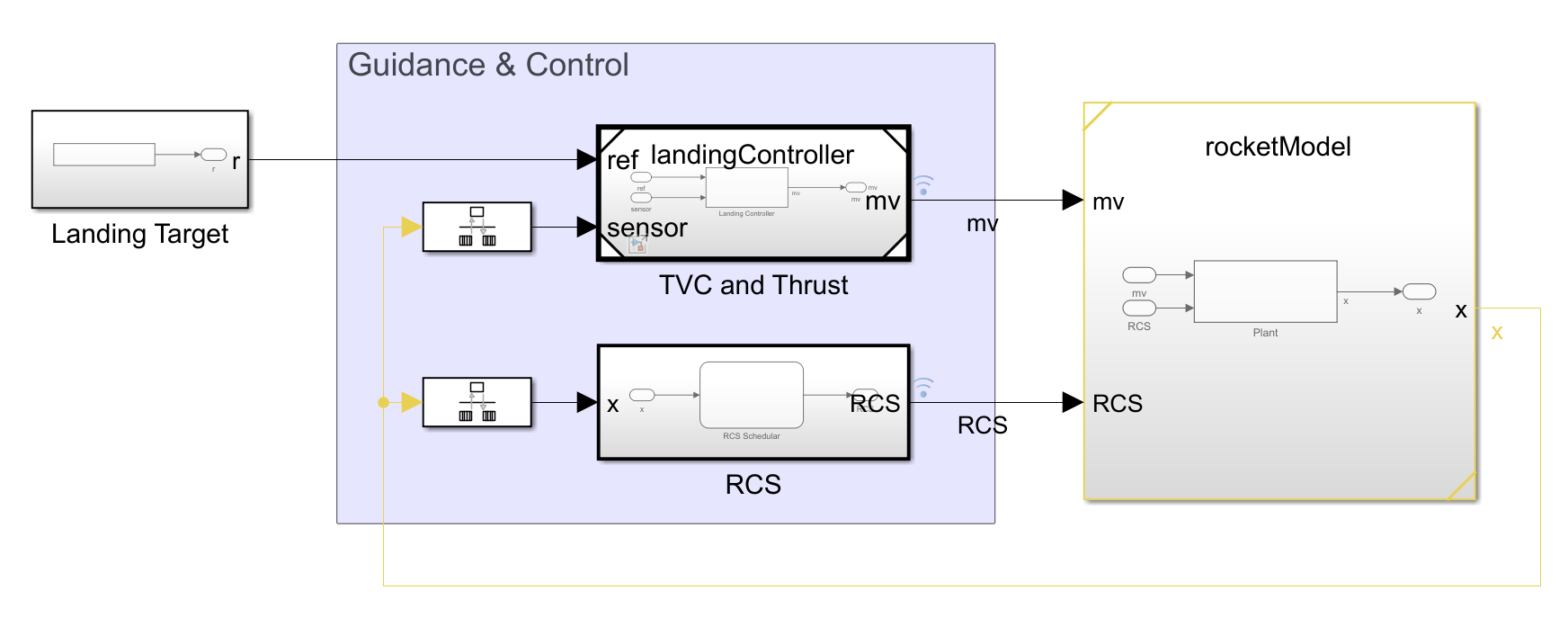
最上位階層におけるシミュレーションモデルの構成は下図の通りです。
向かって右側のサブシステムはロケットのプラントモデル、真ん中が誘導制御部のモデルです。また誘導制御では、上段がTVC(推力偏向制御)および推力の指令をMPCによって計算する部分、下段が補助的な操作量として使用するRCS(姿勢制御用のガスジェット)の指令を計算する部分です。
RCSは機体上部に設けた噴射口から四方にガスを噴射する機構であり、機体のピッチ、ヨーの角度制御を補助的に担わせる構成としています。なお、制御の中身はPIDです。
シミュレーション
では、シミュレーションを実施してみたいと思います。
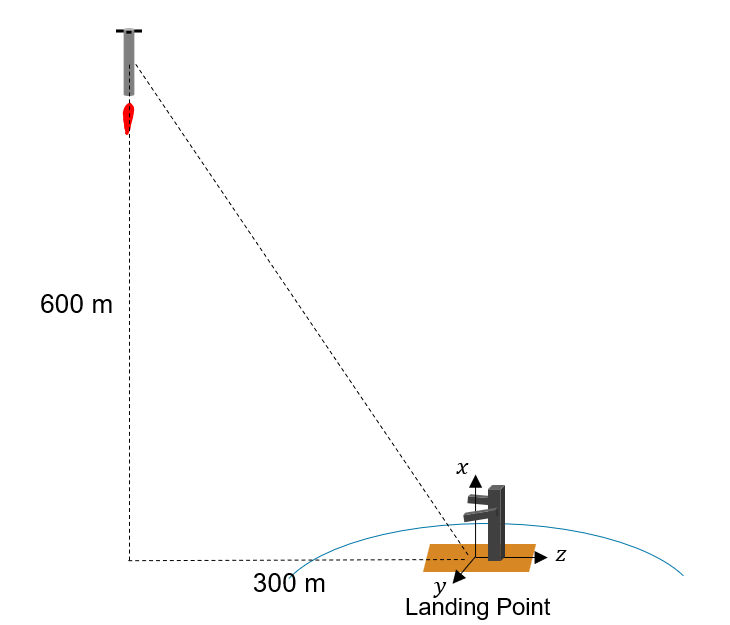
シミュレーション開始時の条件として、高度600[m]、タワーから水平距離で300[m]離れた地点から降下速度50[m/s]、タワーへの接近速度20[m/s]で飛行するシナリオを想定します。
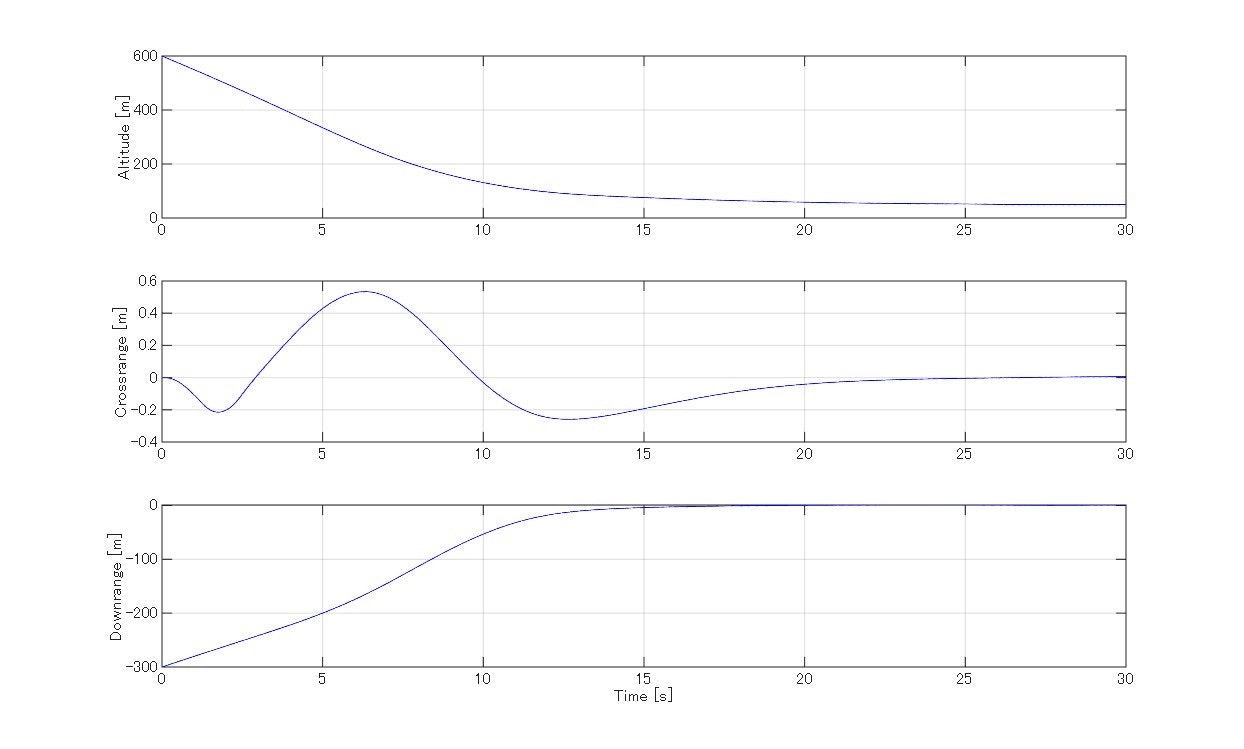
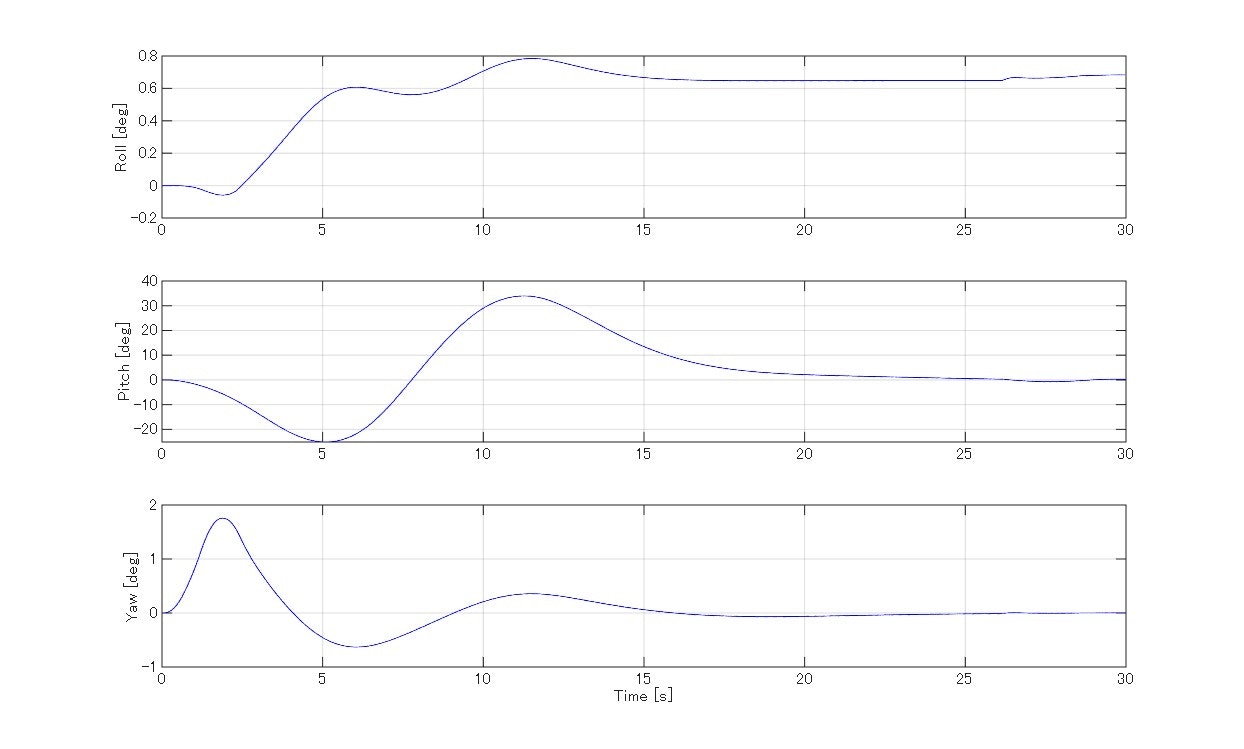
以下がシミュレーションで計算されたロケットの主要状態量のトレンドならびにアニメーションになります。
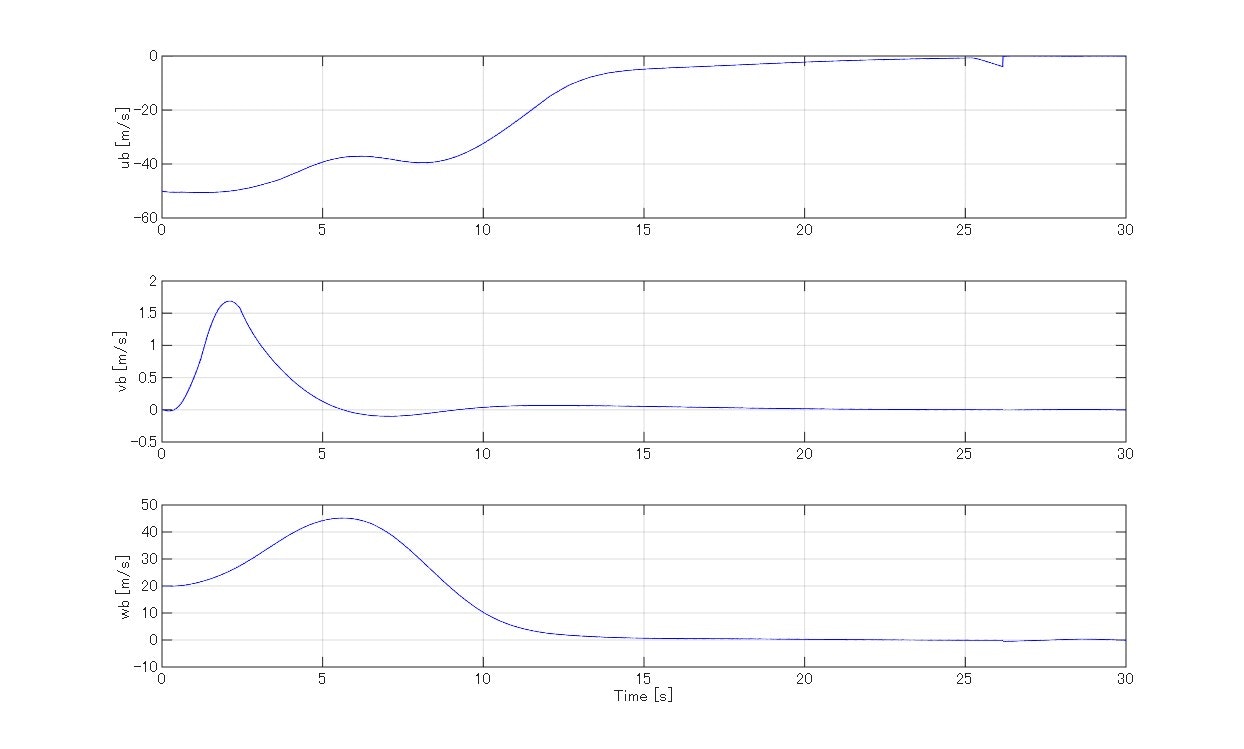
図:制御入力(正規化された推力レベル、TVCのジンバル角度)
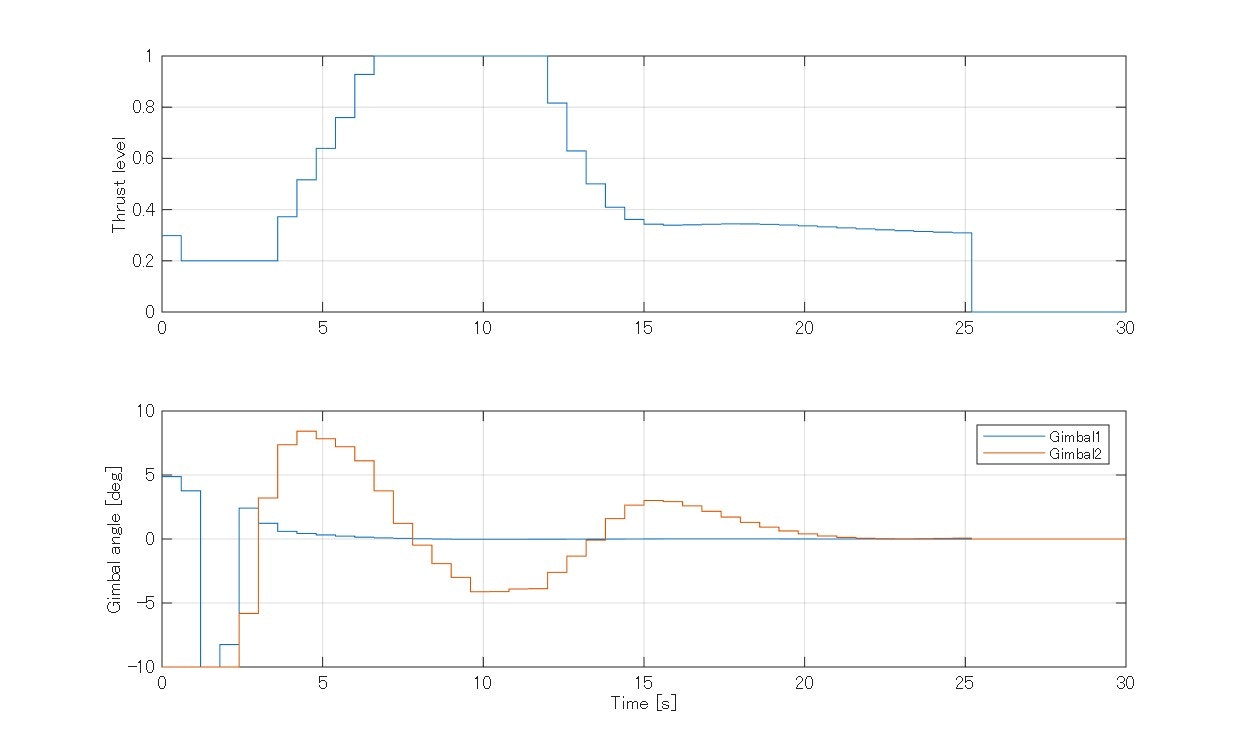
トレンド図ならびに飛行アニメーションから明らかなようにTVC・推力レベルを適切に調整して、機体の姿勢を時折傾けながらタワーに接近し、最後は減速のための姿勢転回を伴いつつゆっくりと降下してお箸でキャッチすることに成功しました。
終わりに
今回の記事ではロケットのお箸キャッチをシミュレーションで試してみました。
実際、SpaceXではこのお箸キャッチを5回目のフライト試験で、かつ初挑戦(だと思われる)で成功させています。
どのようなセンサーを使って、互いの位置を測り、かつどんなタイミングでアームを制御しているのか非常に気になるところです。
なお、このお箸キャッチですが、こんな巨体をどこで支えているのか疑問に思いますが、わかりやすい動画があったので参考に載せておきます。こんな小さな突起で数百トンという重さの機体を支えていると思うと、物理はすごいなと改めて感じます。
そんな再利用ロケット開発ですが、日本でも機運が高まっており、大企業からスタートアップ企業に至るまで挑戦をしています。
その中でもHondaの研究開発子会社である本田技術研究所は、北海道の大樹町というところで試験を実施し、着陸試験を先駆けて成功させています! 自動車や自動運転開発で蓄積してきた技術を結集し、開発している模様です。
Hondaのような大企業以外にも将来宇宙輸送システム株式会社というスタートアップ企業で再利用ロケットの開発に挑戦しています。こちらは、アメリカ製のロケットエンジンを搭載し、米国での打ち上げ試験を計画しているようです。
ぜひ、日本国内からも再利用ロケット開発を推進し、世界に引けをとらない宇宙輸送技術を実現していってもらいたいですね!!
一緒に応援していきましょう🚀