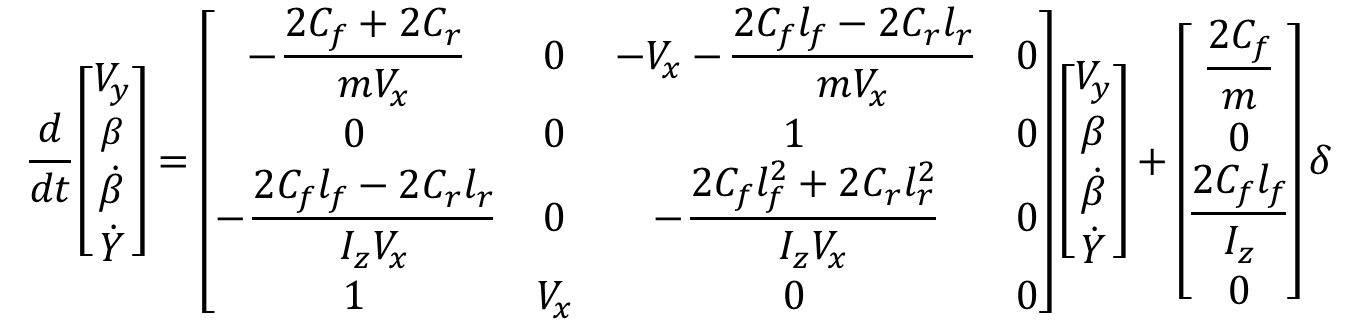はじめに
今回の記事では、PIDのゲインスケジューリング設計についてデータドリブンに基づく手法を試してみたいと思います。
近年、Simulinkの製品ファミリーであるSimulink Control Designにてデータドリブンに基づくオンラインのPIDゲイン自動調整機能がSimulinkのブロックとして登場しています。
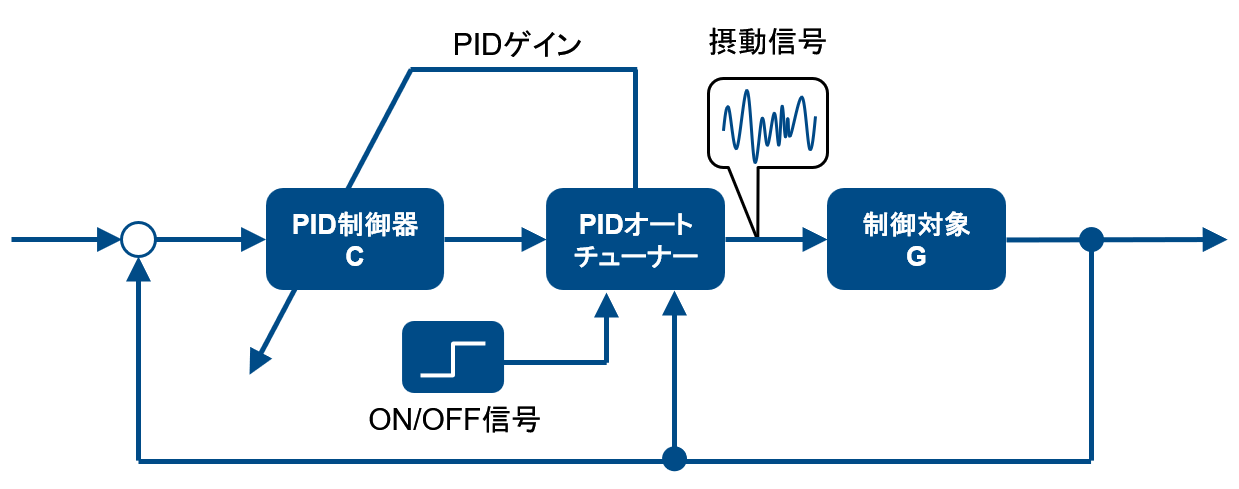
本機能は、制御ループ内の一つのPID制御器について、プラントに対し摂動実験に基づく周波数応答推定とその結果に対する適切なPIDゲインの算出を自動かつオンラインで実施してくれる機能となります。
ユーザーはブロックのパラメーターとして、制御対象$G(s)$とコントローラー$C(s)$を直列結合した一巡伝達関数$L=GC(s)$に対する目標の帯域幅と位相余裕を指定することができ、自動調整のアルゴリズムはこれら目標を可能な限り満足するようなPIDゲイン値を算出します。
また摂動実験のためのテスト信号として、サインストリーム、重ね合わせ、PRBSの3タイプから選ぶことが出来ます。
よって、制御対象の特性や目標帯域幅を考慮しながら適切な振幅を持つ十分な長さの摂動実験を行うことで、プラントの周波数応答を推定することができます。
制御工学的な観点から現実的ではない目標性能を設定したり、十分な摂動実験の結果が得られない場合には、適切な調整結果が得られないケースもあります。
また本ブロックはコード生成の製品であるSimulink Coderを利用することでC/C++コード生成が可能であるため、MCUなどのターゲット上への展開が可能です。ただし、計算リソースやメモリ消費がそこそこあるため、展開できるMCUに限りがあることやプロセッサの能力によっては短いサンプリング周期では計算が回りきらずにタスクオーバーランが発生する可能性もありますので注意が必要です。
Gain-Scheduled PID Autotuner
さて、以下掲載の記事で紹介をしていますが、現実の制御対象は非線形であることが多く、非線形性の影響を受けて単一のPIDゲインでは十分な制御性能を得られなことがままにあります。
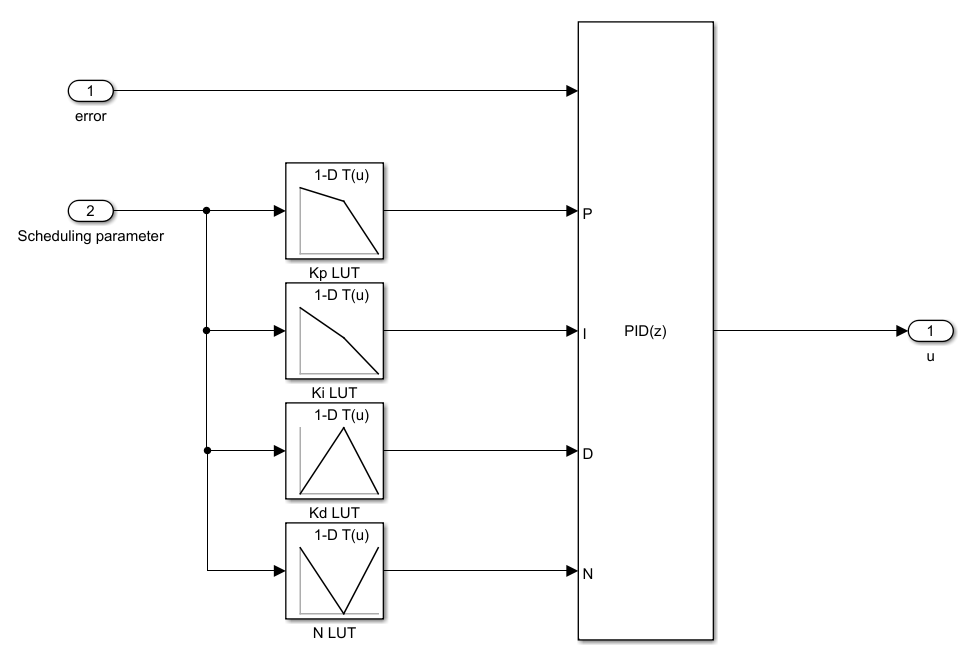
このようなケースでは、下図のように制御対象の非線形性を捉える代表的な因子や指標に基づき、それをスケジューリングのためのパラメーターとしてPIDゲイン値を動的に切り替えるといった運用を行うことがあります。
こうした手法をゲインスケジューリングと呼称しますが、制御対象の非線形性を補償するために利用されている実用的な制御アプローチです。
しかし、このゲインスケジューリングを構築するにあたって問題となるのが、各スケジューリングのポイントにおいてどのようにゲインを設計していくのかという点です。
一般的には、制御対象をスケジューリングパラメーターに応じて定常状態の算出から線形解析し、周波数応答などを見ながら適切な制御器を設計していくという設計アプローチとなります。ゆえに制御対象の数理モデルを導出して各種解析を行わなければならないという手間がかかります。
そのため、直接実験を行って試行錯誤によってゲイン設計/調整されるという現場的な方法で解決がされるケースも多々あります。
ここで、冒頭の自動調整機能の話が出てくるのですが、こちらのブロックがR2024aからゲインスケジューリングの機能をサポートしました。
こちらの機能を使うことで、上記のような数理モデルによる線形解析という手間をデータドリブンな手法で省略することができるため、ある程度取り組みのハードルを下げてくれます。
例題 等価2輪モデルを用いた車両の横方向制御
では、オートチューニング機能を使ったゲインスケジューリングPIDの設計を例題を通じて試してみたいと思います。
題材として、等価2輪モデルによる車両の横方向運動を扱いたいと思います。
ここで、$V_x$は車両重心における縦方向の速度を示しており、40、60、80[km/h]と変化するとします。(※今回縦のダイナミクスは無視します)
なお、今回のモデルを考えるにあたり、以下で公開されているライブラリを利用します。
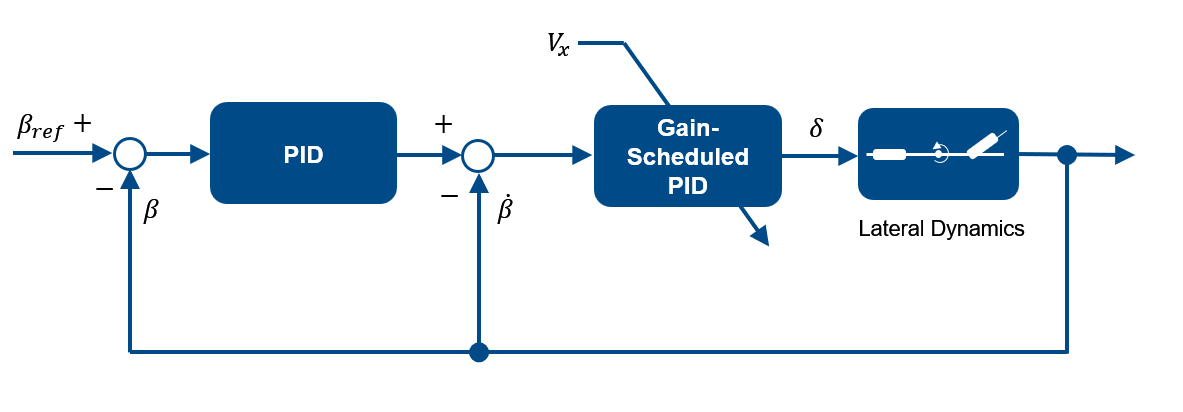
横方向制御系は、下図のように車両のヨー角$\beta$およびヨーレート$\dot{\beta}$についてカスケードなフィードバックループを構成するとし、$\dot{\beta}$について$V_x$をスケジューリングパラメーターとしたゲインスケジューリングPID制御器を適用することを考えます。
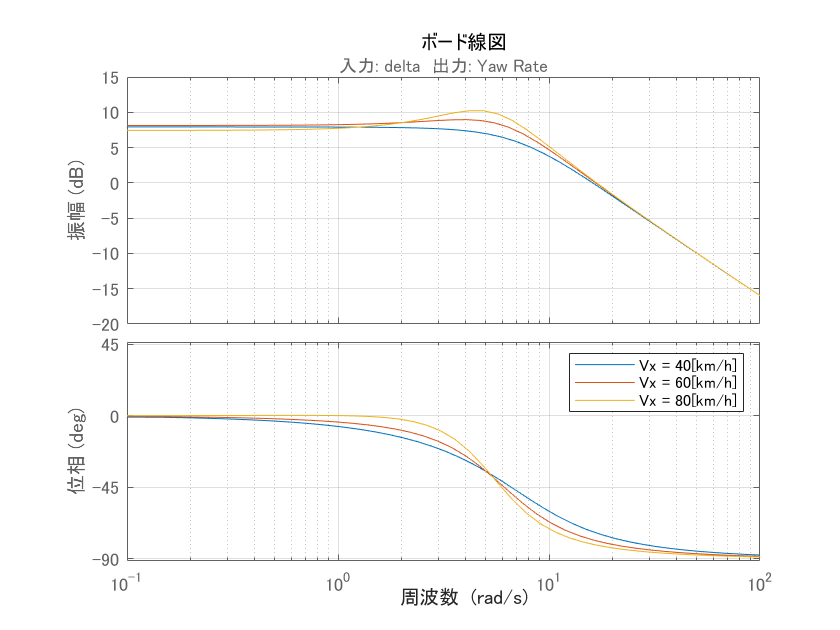
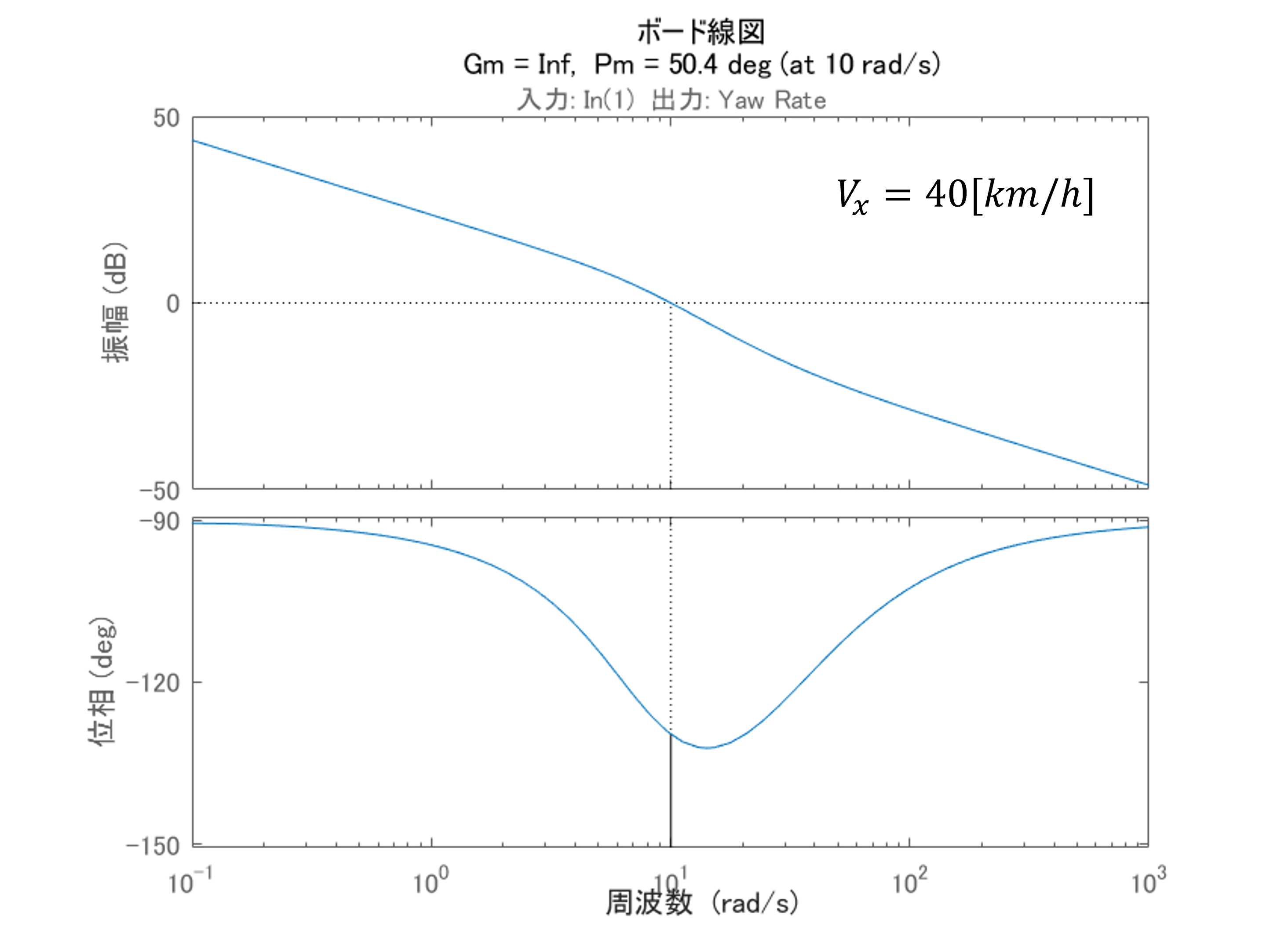
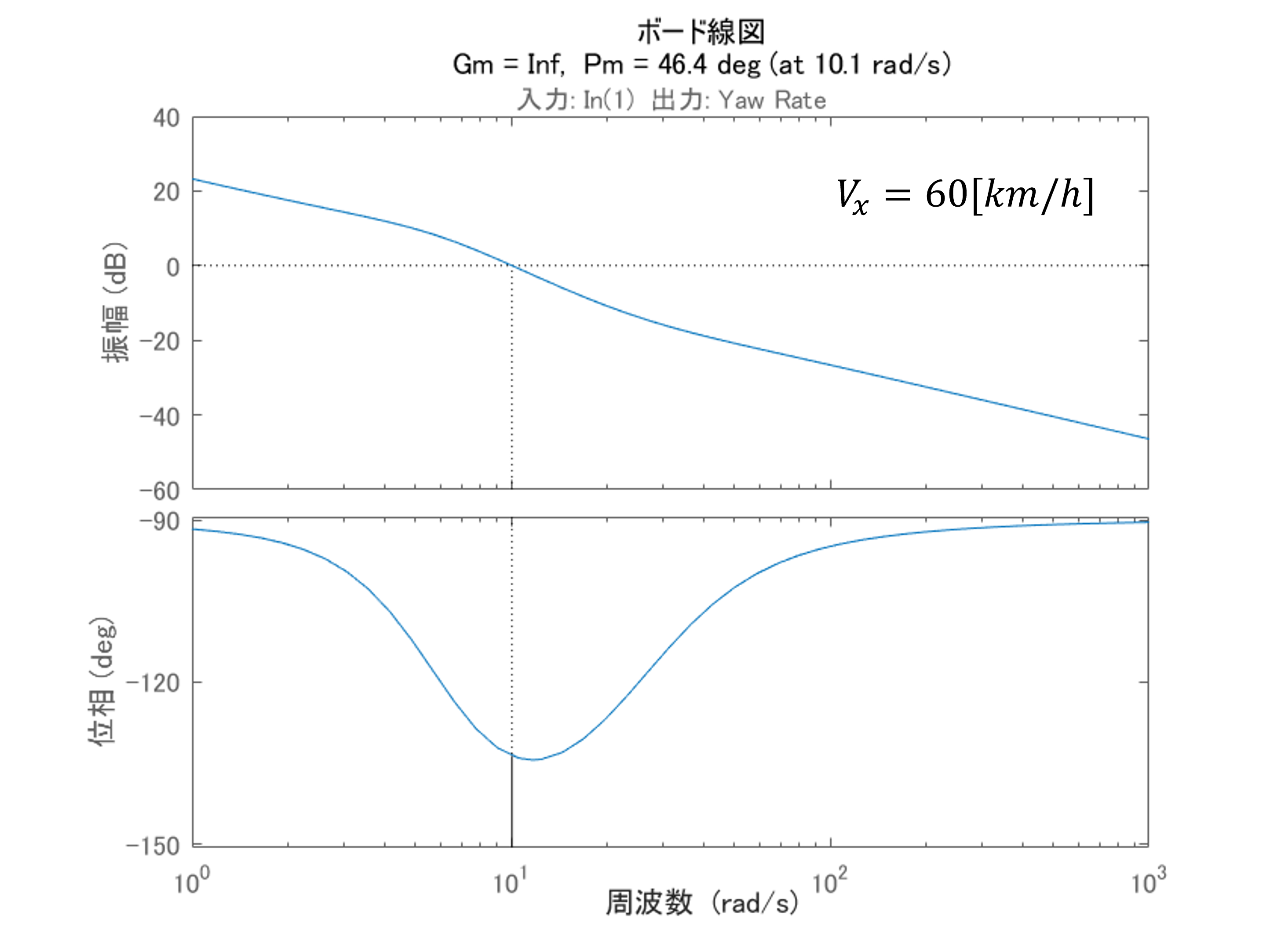
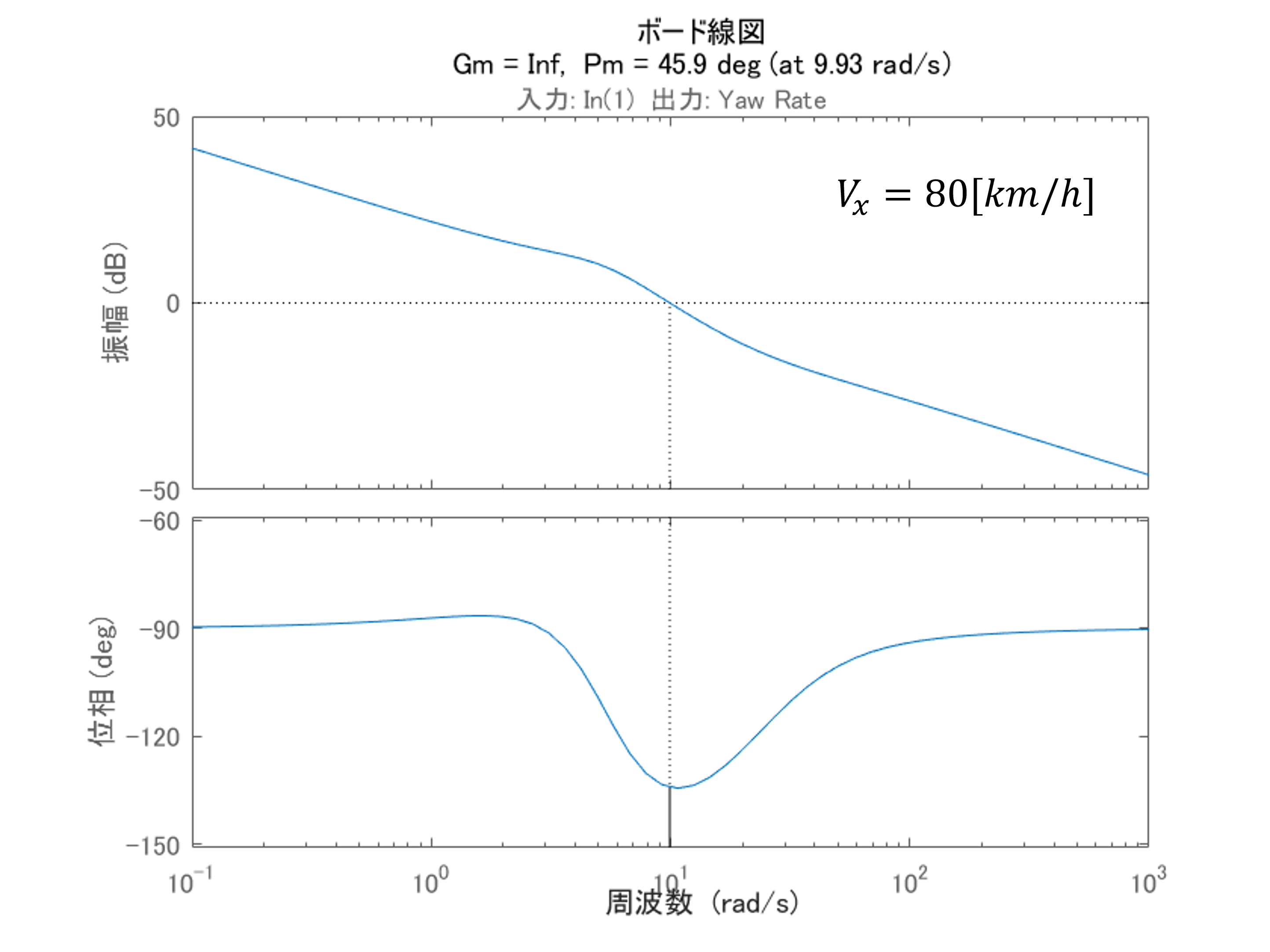
まず、$V_x$の変化によって車両のダイナミクスがどのように変化するのかボード線図を通して確認してみたいと思います。
上図は入力である前輪舵角$\delta$からヨーレート$\dot{\beta}$までのボード線図を示しており、図中3つの速度における応答を線の色を変えて描画しています。
ボード線図から周波数1~10[rad/s]の帯域で差異があることを確認できます。
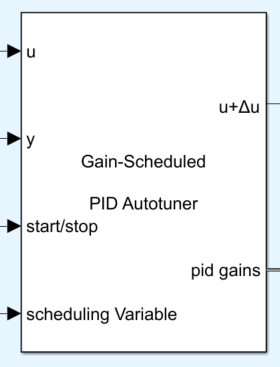
では、この制御対象に対しGain-Scheduled PID Autotunerブロックを利用して、$V_x$に対する適切なPIDゲインの算出を行っていきます。
Gain-Scheduled PID Autotunerブロックをダブルクリックすると下図に示すブロックパラメーターが表示されます。
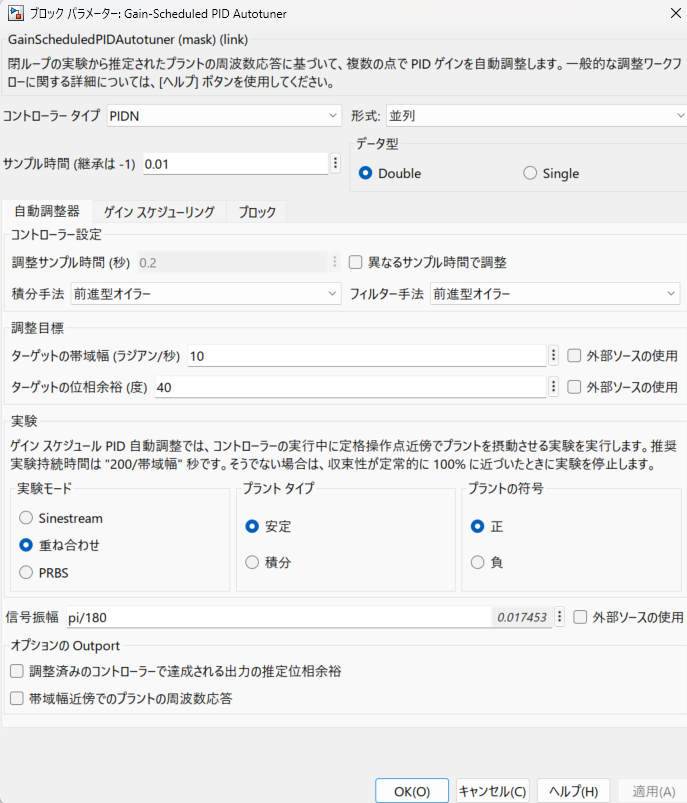
まず自動調整器のタブでは、コントローラーのタイプ、サンプル時間を設定する他に調整目標と実験に関する項目を設定します。
調整目標は前述のように一巡伝達特性$L=GC(s)$に関する目標の帯域幅と位相余裕になります。ここはスカラーでの指定となるので、全設計点で共通のパラメーターとなります。
今回は帯域幅10[rad/s]、位相余裕40[deg]とします。
続いて、実験の項目では、まず実験モードとして摂動信号のタイプを指定します。タイプとしては、こちらも前述の通り、Sinestream・重ね合わせ・PRBSの3つから状況に応じて適切なものを選択することができます。
ここで、選択する信号のタイプと目標の帯域幅との兼ね合いによって、推奨される実験持続時間が決まります。
今回は、帯域幅を10[rad/s]、実験モードを重ね合わせで設定しているため、推奨実験持続時間はダイアログ中の計算式(200÷帯域幅)から20[s]となります。
ここで提示される時間はあくまでも摂動信号のタイプと帯域幅の2つの指標のみによって決まる持続時間であり、制御対象側の遅れやむだ時間の影響が加味されていません。
よって、トータルの遅れも考慮して持続時間が十分か否かを最終的に人が判断する必要があります。
続いて、プラント タイプと符号は制御対象の特性を選択する部分であり、タイプついては ”安定なシステム” or ”積分システム” のいずれかを指定します。
本ブロックはPID制御による既存の閉ループシステムが安定であることを前提としています。使用上の制限事項は以下のヘルプページに詳細が記載されています。
最後に信号振幅の項目にて摂動信号の最大振幅を設定します。これは制御システム内の飽和要素に掛からない範囲で、適切に対象の周波数特性を励起できる値を指定します。
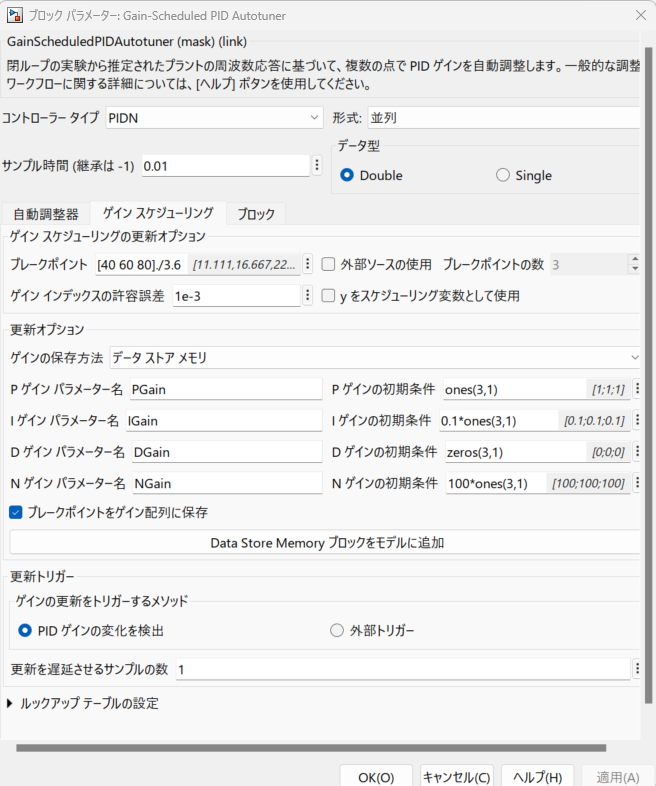
続いて、ゲインスケジューリングのタブでは、スケジューリングのテーブルデータのブレークポイント数とゲインの保存方法、初期値を指定することが出来ます。
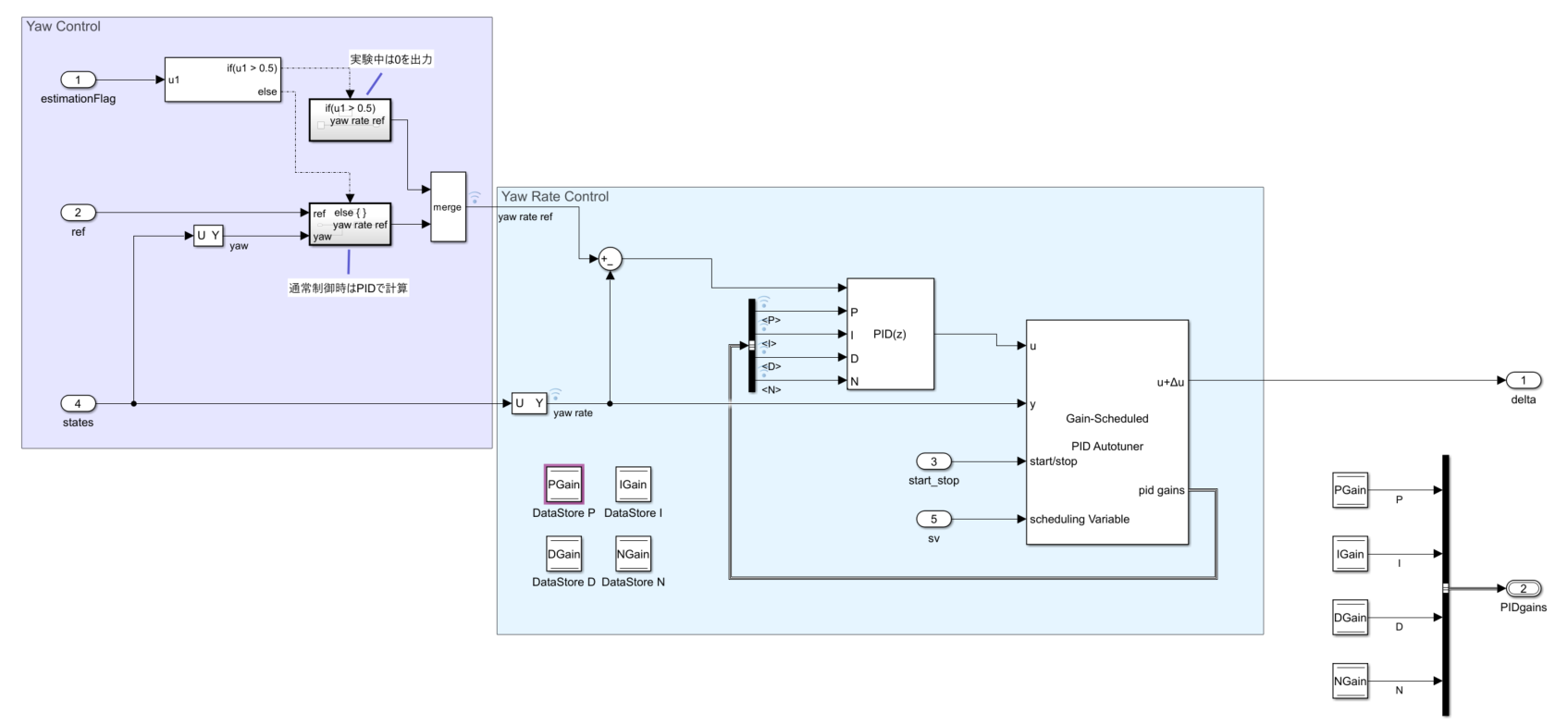
上図が制御器のブロック線図です。
図示している通り、紫で囲っている領域が$\beta$のためのアウター制御ループで、青の領域が$\dot{\beta}$のためのインナー制御ループとなっており、インナーループではGain-Scheduled PID Autotunerブロックを挿入して、前段の$\dot{\beta}$のPIDコントローラーに対しPIDゲイン値を入力しています。
特筆する点としては、$\beta$の制御において実験中と通常制御時でコントローラーを切り替えており、調整中は$\dot{\beta}$の指令値を0[rad/s]に固定しておき、通常制御時はPI制御で状況に応じた指令値を生成します。
なお、本ブロックはシステムが各動作点(スケジューリングポイント)にて定常状態になってから摂動実験を開始することを要求します。
ゆえに、複数の動作点がある場合には、各点に制御対象を持っていく必要があります。
その際に利用できるのが、Change Operating Poinsブロックです。
今回は先ほどのカスケード制御器の上位層に下図のようにChange Operating Poinsブロックを配置し、制御に与える$\beta$の目標値$ref$と実験の$start / stop$信号を管理します。
本ブロックの入力端子$SystemInputs_{in}$はシステムへの入力であり、今回は$\beta$の目標値です。
入力端子$enable/disable$は本ブロックを有効にする/しないの制御信号です。
最後に入力端子$autotuning \ times$はチューニングを開始する時間であり、各動作点における開始時間をベクトルで指定します。
一方、出力端子$SystemInputs_{out}$は本ブロックによって修正された$\beta$の目標値です。
出力端子$start/stop$は各実験のトリガー信号であり、Gain-Scheduled PID Autotunerブロックの同名の入力端子に入力します。
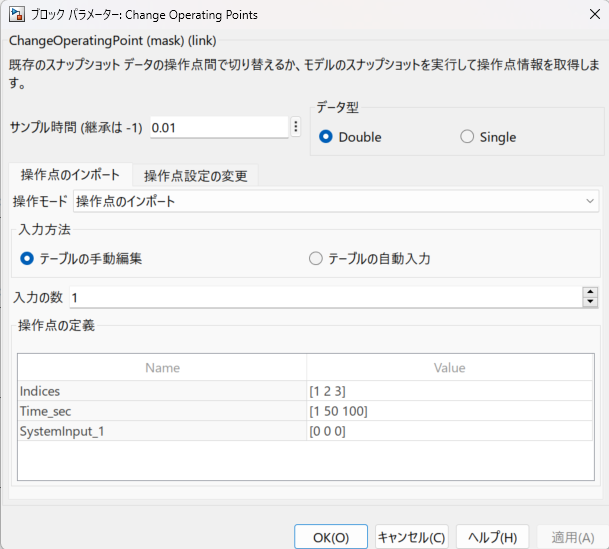
ブロックパラメーターのダイアログを開くと上図のような構成となっており、サンプル時間の指定と操作点のインポートに関するタブ内の項目があります。
ここでは、各動作点に制御対象を持っていくための入力信号を生成していきます。
操作点の定義では、Indices、Time_sec、SystemInput_#(#は入力の数と一致)を設定します。
今回動作点の数は3つ(40,60,80[km/h])あり、各動作点において車両が定常状態$\dot{\beta}=0[rad/s]$であることを実現する必要があります。
各動作点で定常状態が実現できると摂動実験に基づく調整を始めますが、実験の推奨持続時間は前述の通り20[s]であるため、各動作点で20[s]以上実験を行う必要があります。
ゆえに、Time_secはこの時間を加味して各動作点に遷移を開始するタイミングを指定し、SystemInputの各要素は各動作点を実現する入力値を与えます。
今回はすべての動作点で$\dot{\beta}=0[rad/s]$を実現したいので、本項目(すなわち$\beta$の目標値)はすべて0としています。
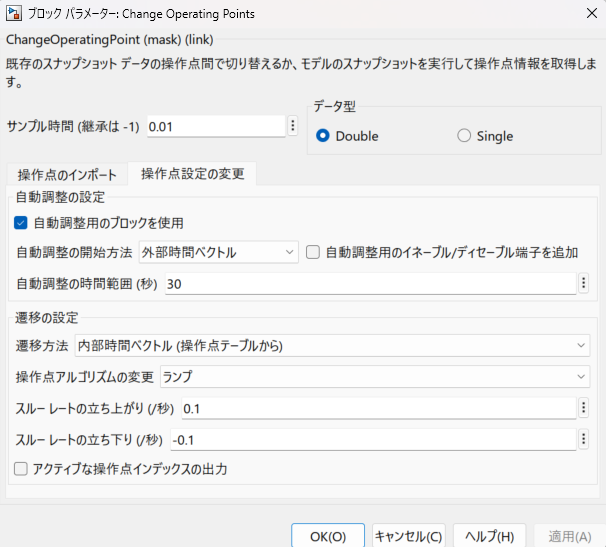
続いて、上図は操作点設定の変更タブに関する項目を示していますが、自動調整の設定にて自動調整の時間範囲を推奨持続実験時間+プラントの応答性も加味して30秒としています。
これが、本ブロックの出力端子$start/stop$の内容に影響を与えます。(後述するシミュレーション結果にて確認)
また遷移の設定では、動作点間を遷移する際のSystemInputに対するレート(変化率)制限を設けることが出来ます。(今回本設定による影響はなし)
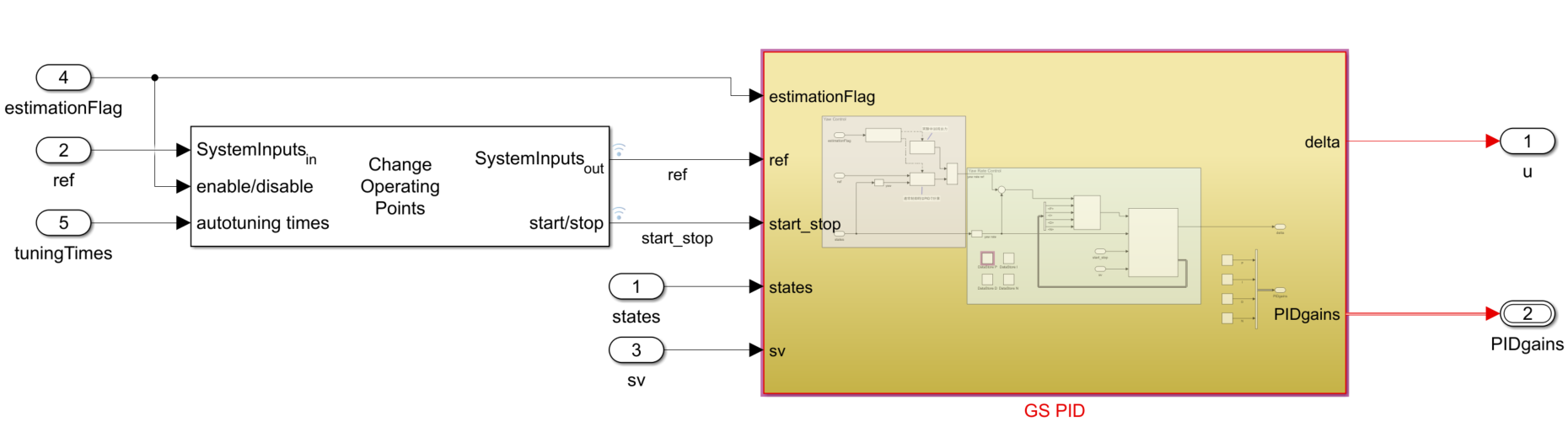
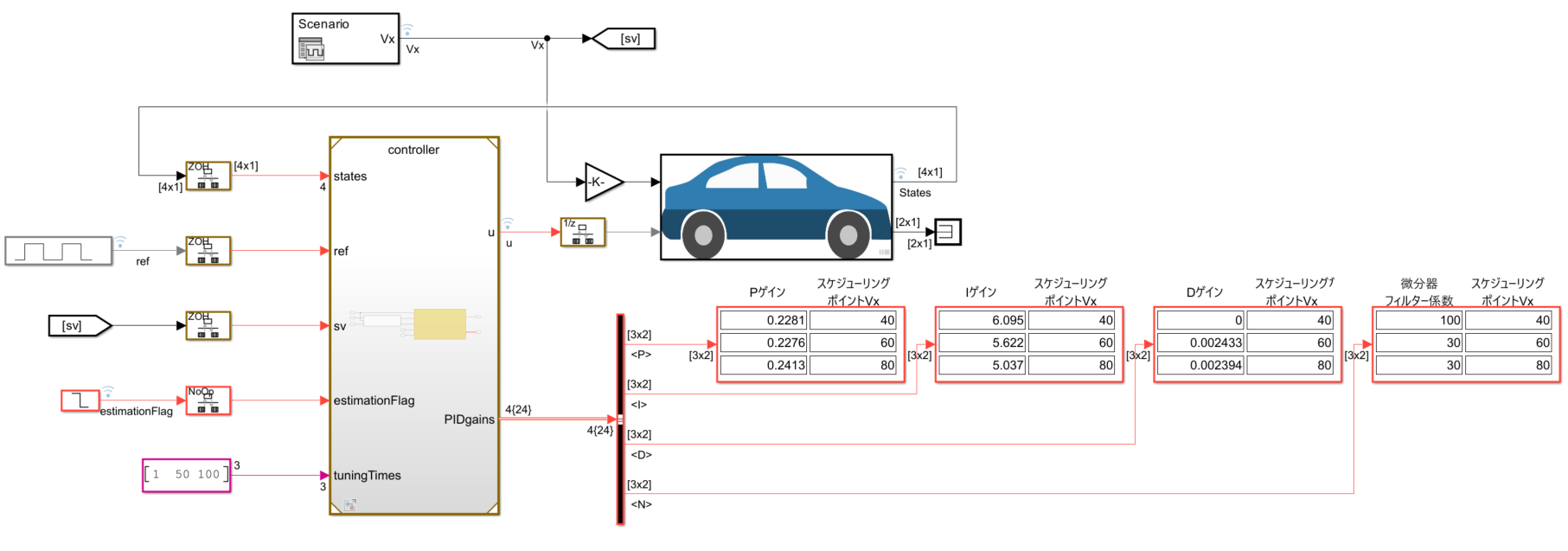
説明が長くなりましたが、モデルの最上位レベルの様子が上図になります。
コントローラーブロックの入力端子$ref$は$\beta$の目標値、入力端子$sv$はスケジューリングパラメーター$V_x$の値、入力端子$estimationFlag$はChange Operating Poinsブロックの$enable/disable$のための制御信号、入力信号$tuningTimes$は各動作点におけるチューニングの開始時間$autotuning \ times $に対応します。
また出力端子$PIDgains$はPIDおよび微分器のフィルター係数Nの4項目について、$V_x$に対する値が格納されます。
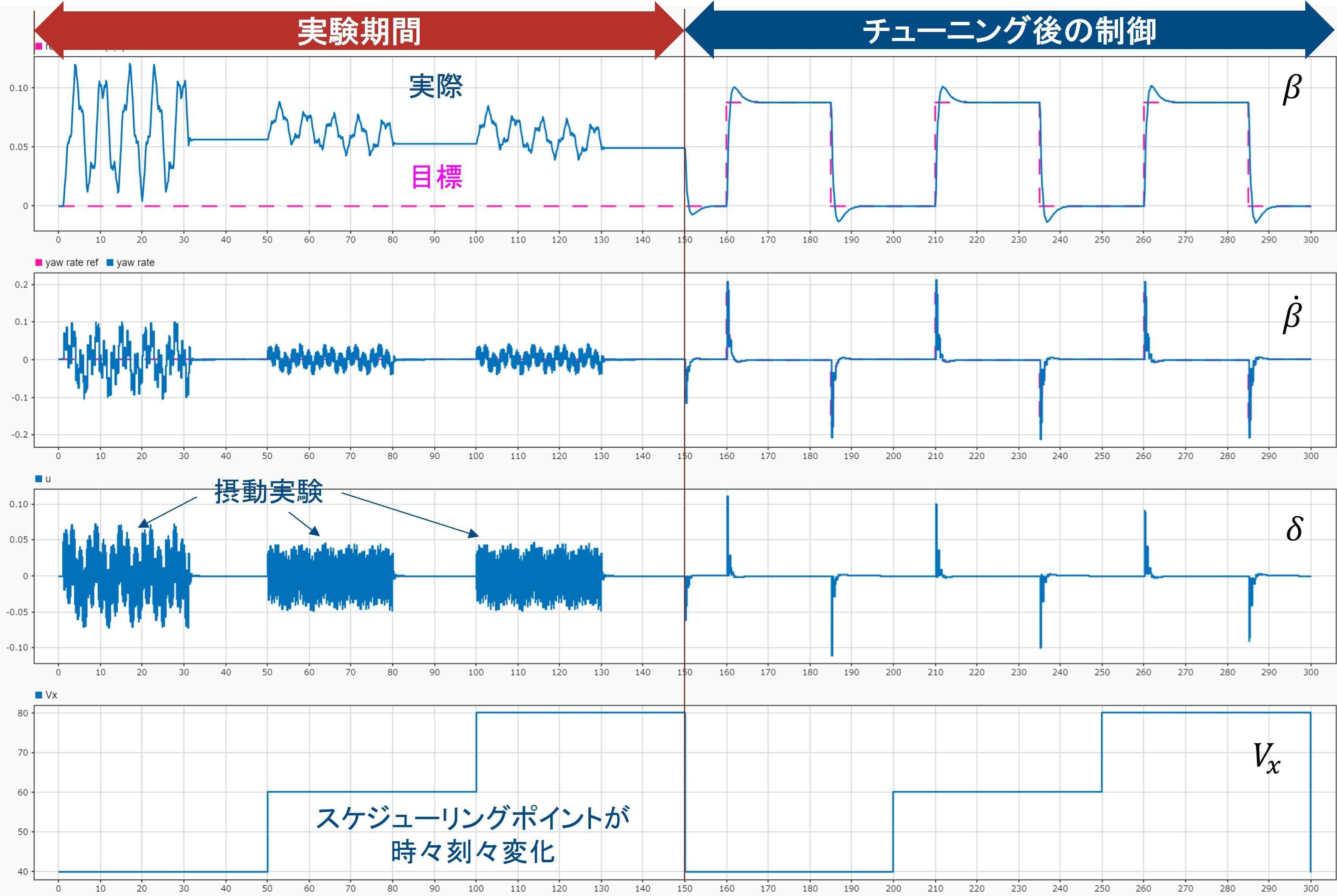
それではシミュレーションを回して結果を確認してみたいと思います。
上図を見ると分かるように入力$\delta$のラインから摂動信号が印可され、それによって制御対象側の状態量に振動が励起されているのが分かります。
またスケジューリングパラメーターである$V_x$に応じて3回テストが実行されています。
実験終了後、PIDゲイン値が更新されて通常の制御に移行していますが、ヨー角$\beta$の目標に対し、良好に追従できていることが分かります。
上図は実験のON/OFFに関する制御信号と各ゲインの様子です。
まず実験の制御信号ですが、$autotuning \ times$として、モデルの最上位レイヤーの端子$tuningTimes$より定数ベクトル信号として1、50、100[s]と与えたため、対応する時間に実験がONとなり、かつ30[s]間ONで保持されていることが分かります。
最終的にすべての実験を終了したら実験のモードそのものをOFFにするため、モデルの最上位レイヤーから$estimationFlag$として与える信号値に基づき、各ロジックをOFFのモードに切り替えています。
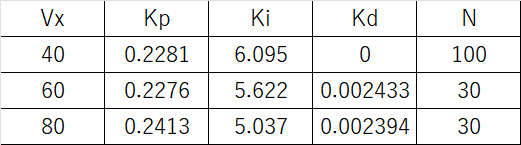
実験終了後はゲインが自動的に更新され、テーブルデータとしてスケジューリングパラメーター$V_x$に応じて動的に変更されるようになります。
値として、上表のような結果となりました。
実際にこれらの値を使って、指定した目標の帯域幅、位相余裕が満たされているかを一巡伝達特性$L=GC(s)$を計算し確認してみます。
上図は$V_x$に対する安定余裕をmarginコマンドを使って計算した結果です。
結果から分かる通り、概ね10[rad/s]でカットオフしており、かつ位相余裕が40[deg]以上確保されています。
%% 制御対象の特性
Vx = [40 60 80]./3.6;
sys = cell(length(Vx),1);
% 等価2輪モデルの関数(R2024aからローカル関数はどこでも定義可能に)
function sys = stateFcn(Vx)
% Model parameters
m = 1575;
Iz = 2875;
lf = 1.2;
lr = 1.6;
Cf = 19000;
Cr = 33000;
% Continuous-time model
A = [-(2*Cf+2*Cr)/m/Vx, 0, -Vx-(2*Cf*lf-2*Cr*lr)/m/Vx, 0;
0, 0, 1, 0;
-(2*Cf*lf-2*Cr*lr)/Iz/Vx, 0, -(2*Cf*lf^2+2*Cr*lr^2)/Iz/Vx, 0;
1, Vx, 0, 0];
B = [2*Cf/m 0 2*Cf*lf/Iz 0]';
C = [0 0 1 0];
D = zeros(1,1);
sys = ss(A,B,C,D);
sys.InputName = {'delta'};
sys.OutputName = {'Yaw Rate'};
end
for i = 1:length(Vx)
sys{i} = stateFcn(Vx(i));
end
% ボード線図の描画
figure(1),clf
bode(sys{1},sys{2},sys{3}),grid on
legend('Vx = 40[km/h]','Vx = 60[km/h]', 'Vx = 80[km/h]')
%% チューニングによるPID制御器を用いた開ループ特性の安定性評価
Kp = [0.2281 0.2276 0.2413];
Ki = [6.095 5.622 5.037];
Kd = [0 0.002433 0.002394];
N = [100 30 30];
C = cell(length(Vx),1);
GC = cell(length(Vx),1);
for i = 1:length(Vx)
C{i} = pid(Kp(i),Ki(i),Kd(i),1/N(i),0.01); % PID制御器の構築
GC{i} = sys{i}*d2c(C{i}); % コントローラーは離散から連続時間に変換
end
figure(2),clf
margin(GC{1})
figure(3),clf
margin(GC{2})
figure(4),clf
margin(GC{3})
さいごに
今回はデータドリブン手法に基づくゲインスケジューリングPID制御器の設計を行ってみました。
ゲインスケジューリング制御は設計点の算出と各点における制御特性の解析ならびに制御器の設計が必要となる煩雑なワークフローとなりますが、今回試したようなデータドリブン手法では、手動による制御対象の特性解析とPIDゲインの算出を自動化してくれます。
ただし、便利でありつつもその反面アルゴリズムにすべてお任せではなく、最後は人による制御工学的な視点に基づく洞察、解釈が必要です。