はじめに
機械学習ではデータの分布を正規分布に近づけると、予測精度が改善する場合が多々あります。正規分布に近づける手法の一つとして、boxcox変換が存在します。
boxcox変換
boxcox変換は対数変換などと異なり、多様な分布を正規分布に近づけることが可能であるため、様々なデータに応用可能です。本記事では以下の処理をPythonで実行します。
- Pythonでboxcox変換を行う
- boxcox変換後のデータをもとに戻す
boxcox変換の詳細な説明は省略しますが、下記のサイトで分かりやすく説明されています。
Box-cox変換を用いて正規分布に従わないデータを解析をしてみよう!
Box-Cox変換を理解してみる
環境
- Google Colaboratory Pro
コード
モジュールのimport・変換前のデータ
import pandas as pd
from sklearn.datasets import load_boston
import seaborn as sns
from statistics import mean, median, variance, stdev
from scipy.stats import boxcox
from scipy.special import inv_boxcox
データとしてscikit-learnのBoston house-prices (ボストン市の住宅価格)を使用します。
boston = load_boston()
y = boston.target
変換前の各指標を計算します。
m = mean(y)
med = median(y)
vari = variance(y)
std = stdev(y)
print("平均: ", m)
print("中央値: ", med)
print("分散: ", vari)
print("標準偏差: ", std)
#実行結果
平均: 22.532806324110673
中央値: 21.2
分散: 84.58672359409854
標準偏差: 9.197104087379817
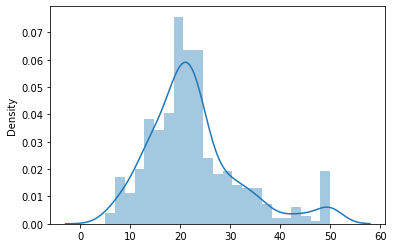
変換前のpriceの分布をヒストグラムで描画します。
sns.distplot(y)
boxcox変換・変換後のデータ
boxcox変換を実行します。
y_boxcox = boxcox(y)
boxcox()の戻り値について調べます。
print(type(y_boxcox),"要素数:",len(y_boxcox))
print("変換後のデータ: \n",y_boxcox[0][:10])
print("λ値: ",y_boxcox[1])
#実行結果
<class 'tuple'> 要素数: 2
変換後のデータ:
[4.57293637 4.36558166 5.33694273 5.25495447 5.42860689 4.93592663
4.48001683 4.81796329 3.85654088 4.10949441]
λ値: 0.2166209012915364
boxcox()の戻り値は要素数2のタプルです。1つ目の要素が変換後の値(リスト)で、2つ目の要素がλ値というboxcox変換にて使用されるパラメータです。このλ値を参照することで変換前の分布に戻すことも可能です。
変換後の各指標を計算します。
m_boxcox = mean(y_boxcox[0])
med_boxcox = median(y_boxcox[0])
vari_boxcox = variance(y_boxcox[0])
std_boxcox = stdev(y_boxcox[0])
print("平均: ", m_boxcox)
print("中央値: ", med_boxcox)
print("分散: ", vari_boxcox)
print("標準偏差: ", std_boxcox)
#実行結果
平均: 4.326198793674132
中央値: 4.329286356920582
分散: 0.6132144144256096
標準偏差: 0.7830800817449066
平均値≒中央値となり正規分布に近づいています。
変換後の分布をヒストグラムで描画します。
sns.distplot(y_boxcox[0])
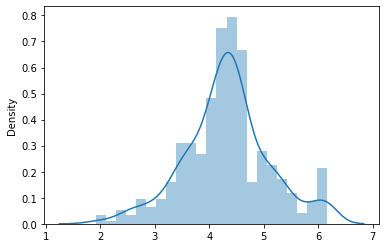
中央値を中心として左右対称となり、正規分布に近づいています。
inv_boxcox変換・変換後のデータ
変換後のデータを変換前の分布に戻します。戻すにはinv_boxcoxモジュールを使用します。(invはinverseの略で反対の意味です。)
y_inv = inv_boxcox(y_boxcox[0],y_boxcox[1])
inv_boxcox変換後の各指標を計算します。
m_inv = mean(y_inv)
med_inv = median(y_inv)
vari_inv = variance(y_inv)
std_inv = stdev(y_inv)
print("平均: ", m_inv)
print("中央値: ", med_inv)
print("分散: ", vari_inv)
print("標準偏差: ", std_inv)
#実行結果
平均: 22.532806324110673
中央値: 21.199999999999992
分散: 84.58672359409854
標準偏差: 9.197104087379817
boxcox変換前の値に戻っています。
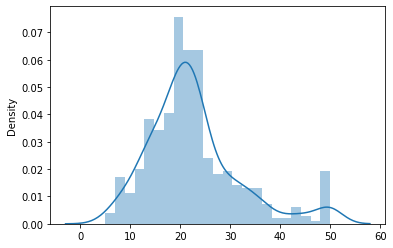
inv_boxcox変換後の分布をヒストグラムで描画します。
sns.distplot(y_inv)