E(1) + E(2) = E(3)？同型暗号化。暗号化されたまま演算を行う技術

最近、興味深い話題を偶然接することがあって、それが完全同型暗号という話題でした。
暗号学や本格的な数学的アプローチに関しては苦手な方ですが、勉強がてらいろいろ資料を参考し、整理した内容となります。もし誤った内容などあれば、ご指摘いただけると幸いです。

1. 同型暗号とは

1) 定義

暗号文に対して、暗号化された状態のまま、特定演算を遂行できる暗号化方法

2) 特徴

• 暗号文の状態で特定演算を遂行できるアルゴリズムを提供
• 演算結果は新しい暗号文であり、復号した結果は「平文に対して演算した結果」と同様

3) 概念

A) 一般的な暗号化方式においての演算課程

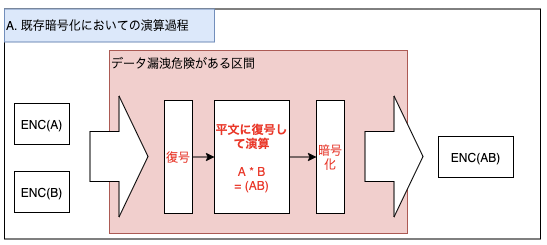
図Aは、一般的な暗号化方式においての演算課程を表しています。
一般的には暗号化されたデータに関して、平文を使った何らかの演算を行いたい場合は、まず復号をして平文を出した上で演算を行い最暗号化するということが一般的です。

しかし、この場合、以下の状況がどうしても生まれるようになります。
- ①暗号化・復号キーを、双方持っていなければならない。
- ②演算する区間では、どうしても平文がオープンされる。

①の場合は、RSAなど非対称キー方式にすると、ある程度キーの管理において安全にはなりますが、②の場合はどうしても、一度平文がオープンされるのに対して、時々いろいろ問題になったりします。

B) 同型暗号化における演算家庭

図Bの場合は、同型暗号化における演算家庭を表しています。
図Aとは違い、暗号化されたまま、特定演算を行う方法を同型暗号化は提供します。
その演算の結果は、新しい暗号文になり、復号したときには、平文に対して演算した平文の結果と一致することを保証します。

これにより、
- ①暗号化・復号キーを、演算区間では持つ必要がなくなります。
- ②演算する区間では、平文がオープンされないため、暗号化・復号した本人以外には平文の漏出がされません。

このように、同型暗号化は、暗号化されたまま演算する方法を提供することで、より安全なデータセキュリティを行える方法となります。

5) 簡単な例示

では、よりふかぼって、実際の動作イメージを書いてみましょう。

今回は、すごく単純な暗号化ロジックでその例えを説明しますが、実際のところは、すごく複雑な数学的設計から、同型暗号は成り立つということを意識した上で見ていただけると幸いです。

A) 暗号化・復号要件

同型暗号の原理を説明するため、以下の要件として暗号化・復号・演算に対して定義します。

• 平文と、キーは、整数のみとする
• 暗号化関数は、平文 * キーを遂行し暗号化する
  • E(x) => x * __KEY__
• 復号関数は、暗号文 / キーを推敲して復号する
  • D(x) => x / __KEY__
• 同型を保証する演算としては、足し算のみとする
  • HE_ADD(ex, ex) => ex + ey
• 足し算演算に対しては、以下の条件を保証する
  • 復号せず、暗号化されたまま演算し、新しい暗号文を結果としてリターンすること
  • 結果を復号した平文と、平文に対して同じ演算をした結果は、相同であること

B) 暗号化・復号の流れ

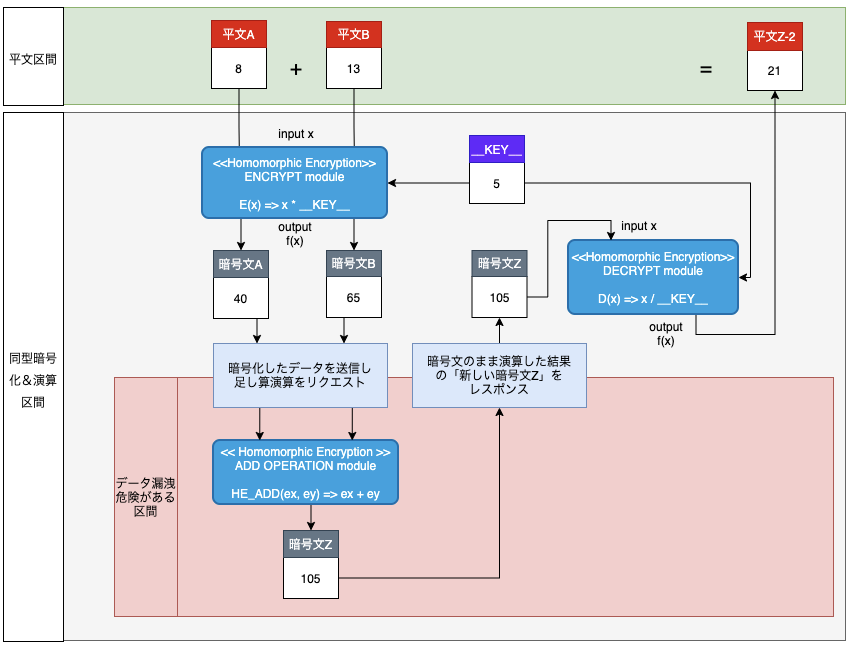
上記の要件を元に、以下を想定して暗号化と復号を行う事例を図式として表現します。

• ８と13を、それぞれ同型暗号化要件に従い暗号化し、演算は外部へ委託する
• 同型暗号化要件に従い、外部では、暗号化されたまま足し算演算を遂行し、新しい暗号文を結果として、応答する
• 応答をもらった後、復号した平文は、平文同士の足し算の結果と一致することを確認する

• まず最初に、ENCRYPT moduleの演算で、平文を暗号化します。キーは５なので、暗号化を遂行すると、平文Aは８から、暗号文Aの８０になります(8 * 5)。平文Bは１３から、暗号文Bの６５になります(13 * 5)。
• その後、暗号文を伝達し、ADD OPERATION moduleで、足し算演算を遂行するようになります。暗号文Aと暗号文Bを、暗号化されたまま足し算をすると、１０５になります。これは演算結果であり、新しい暗号文になります。
• では、暗号文Zである１０５を、DECRYPT moduleで復号します。キーは暗号化に使ったものと同じ５です。復号演算を遂行すると、その結果は21になります(105 / 5)。
• 21という結果は、平文同士の足し算である、8 + 13の結果と一致することを確認できます。

すごく単純ですが、掛け算で暗号化・割り算で復号の暗号化は、足し算に関して暗号化されたままの演算を提供するので、一種の同型暗号の例と言えると思います。

2. 分類

しかし、同型暗号というのは、処理速度の低下やデータ汚染を起こさないまま、実際に我々に必要な演算機能を提供し、要求条件を満たすのはすごく難しいと言えます。

その故、長い間、部分的に同型を保証する部分同型暗号が主であり、演算速度が非常に遅い問題で使われてなかったものが、最近になって飛躍的な速度改善と優れたアルゴリズムが出たり、いろんな企業から研究されたりとかで、基本的な演算に対しては、完全な同型を提供する完全同型暗号も、導入を試みる動きが活発になりました。

A) 部分同型暗号　(partial homomorphic encryption)

定義としては、暗号化されたままの状態で,以下の制約がつく上で、同型を保証する暗号化方式を意味します。

• コンピューターができる演算のうち、一部の演算を提供する
• 演算回数に制限がある

この記事であげら例も、コンピューターができる演算の中で掛け算のみ、同型を保証するという制約があるため、部分同型暗号に属すると言えます。

「演算回数に制限がある」というのは、暗号化された状態で演算を繰り返す場合、平文に対してデータ汚染「noise」が発生する問題があったため、回数制限という制約があったのが背景となります。

筆者も詳しくはないですが、以下のものが代表的な部分同型暗号になります。

• ELGamal : 掛け算のみ保証
• Pailler : 足し算のみ保証
• Gentryが提案したSHE（部分同型暗号）同型暗号（noise問題があり、演算回数に制限あり）
  • ※以降、Gentryがbootstrapingの概念を作り、FHE（完全同型暗号）を発表
• RSAも、暗号化された状態で掛け算を遂行できるため、一種の同型暗号と言える

B) 完全同型暗号 (fully homomorphic encryption)

完全同型暗号は、以下の条件を満たす同型暗号を意味します。

• コンピューターで行える全ての演算を遂行できる ※１
• 回数制限などなく、必要に応じて演算が行えて、同型を保証する

たとめば、演算を繰り返しても、noiseによる平文の汚染を防ぎながら演算が遂行できるようにするため、発生したnoiseを、平文を維持しながら、noiseをリセットし新しい暗号文を生成する方法であるBootstrappingという課程で、可能とする原理があります。
具現原理に関しては、自分にも難しい部分ですが、特徴を記載しておきます。

※ Bootstrapping
- 暗号化されたキーと、二重に暗号化された暗号文を入力した後、復号を遂行し、新しい暗号文を生成（Recrypt）。同型演算の後、毎回Recryptを遂行しFHEを生成
- 暗号文に暗号化された秘密キーを利用し、ノイズが減少した新しい暗号文を生成後、演算を遂行する原理

現在、研究されている同型暗号とは、2009年Gentryが提案した、任意の演算を無限に繰り返すことができる完全同型暗号を前提としています。

3. 歴史・世代

1) 同型暗号の誕生

初めて同型暗号の概念が発表されたのは、1978年RAD78論文です。

以降、Exclusive-OR演算に対して同型を保証するGoldwasswer-Micali82(1982)、足し算に対して同型を保証するOkamoto-Uchiyama cryptosystem(1998)とこれを改善したPailler(1999)や、掛け算に対して同型を保証するElGamalなどが発祥されました。

しかし、上記の技術は、ごく一部の演算のみ可能か、衰弱性が報告され、実活用に困難な部分がありました。

1) 完全同型暗号の登場

2009年、IBMの研究員であるGraig Gentryによって、完全同型暗号が発表されました。
この技術は、足し算と掛け算を同時に同型を保証することができ、理論上ではコンピューターで遂行できる全ての演算に適用できる可能性を示しました。
しかし、最初は１bitの演算に30分ほどかかるほど、処理速度が遅いという問題がありました。

この技術が、完全同型暗号の第１世代と分類されます。
それ以降、以下のように世代を重ねながら、さまざまな改善が行われ、現在を活発な研究が行われてます。

●１世代

2009年 IBMのGraig Gentryによって初めて提案された完全同型暗号

●２世代

2011年 Brakerski-Gentry-Vaikuntanathanによって発表された論文では、掛け算に対してノイズを大きく減少できる方法が提案され、bootstrappingせず掛け算ができる回数を改善。modulus、またはkey-switching課程と呼び、このスキームを導入した同型暗号を第２世代と分類する

The Brakerski-Gentry-Vaikuntanathan (BGV, 2011) scheme
The NTRU-based scheme by Lopez-Alt, Tromer, and Vaikuntanathan (LTV, 2012)
The Brakerski/Fan-Vercauteren (BFV, 2012) scheme
The NTRU-based scheme by Bos, Lauter, Loftus, and Naehrig (BLLN, 2013)

●3世代

2013年 Gentry-Sahai-Waterによって発表された論文では、２世代からさらにノイズを減少させ、同型の掛け算で多くの演算を必要とする再線形化(relinearization)課程なしで可能とする技術を発表。このスキームを導入した同型暗号を第３世代と分類する

Ducas-Micciancio14のFHEW Scheme
Chillotti-Gama-Georgieva-Izabachene16の TFHE Scheme

●４世代

２０１６年、Cheon-Kim-Kim-Songは、足し算と掛け算に加えて、切り上げ演算が暗号化状態で可能なHEaaN同型暗号を発表。
既存の同型暗号は切り上げ演算が可能ではあったが、Bootstrappingほど演算時間を要する非常に複雑な演算が必要だたが、HEaaNは足し算水準の演算時間で処理できるようにし、算術演算において大幅な改善をした。

そして、bitごとに３０分かかっていたBootstraping演算が、2019年では0.5msまで改善し３００万倍の速度改善が行われ、HEaaNは今までの演算速度の問題に対して大幅に貢献した。それにより機械学習など近似演算を活用する応用分野への商用化が可能となった。

これを、第４世代と分類する。

4. 長所・短所

1) 長所

暗号文を復号せずとも、算術演算はもちろん、検索や統計処理、機械学習なども可能であり、データを処理する課程で復号が不要なため、データ漏洩や、キーの漏洩の危険が少なくなる長所があります。

2) 短所

短所は以下のものがあります。

暗号文のサイズが膨大

• 既存暗号文のサイズに比べて、１０倍から１００倍まで、同型暗号の暗号文のサイズは大きくなる可能性がある

処理に時間がかかる

• 暗号化・復号の時間が、RSAに比べて数十倍かかる可能性がある
• 掛け算演算に対しても、数百msがかかる可能性がある
• ノイズによる平文汚染の防止のためのBootstrapingの時間が必要で、2015年基準だと、１回で0.02秒くらいかかると報告されていた。

3) 今後の短所の克服

実のところ、最近までも、明確な長所はあるものの、技術的課題による短所がかなり障壁になっており、活用が難しいのが現状でした。

しかし、マシーンの性能の発展とアルゴリズムの改善が活発になり、最近２〜３年は、１０００倍以上の性能改善が行われたといわれます。それでも、平文データ処理に比べて数百倍から数千倍遅い状況ではありますが、GPU演算、並列処理、専用ハードウェアチップ開発など、さまざまな研究が行われており、近いうちに飛躍的な改善が行われることが期待されます。

5. 活用分野と展望

まだまだ、発展途中ではありますが、いろんな分野で活用されることが、今後期待されてます。
その例として、以下の三つを記載しますが、それ以外でも、機微な情報の扱いが求められる分野で活用可能性はあります。

1) 金融分野・医療分野

銀行、クレジットカード、保険など、金融分野では、データ分析とトランザクション処理などが強く求められる分野ですが、機微な情報が前提となるため、色々難しいところがあります。

しかし、同型暗号化を基盤とする同型演算・データ分析・機械学習が可能になることで、プライバシーデータの機密性は保ちながら、必要な処理を行うことができると期待されています。

実際に、信用評価システムにおいて、同型暗号化されたデータの状態で、機械学習を行い、信頼性・正確性・安全性が確保された信用評価のモデルを検証することができたという事例もあるそうです。

医療分野もまた、機微なプライバシーデータを扱いますが、今後同型暗号技術が適用されれば、医療機関同士の情報連携なども、有効活用できると期待されています。

2) 生体認識分野

指紋など、生体情報を利用した認証が最近は良く使われてますが、同型暗号技術を適用すると、生体情報を復号し平文で保管したり、検証のため元データを転送したりする必要がなくなり、暗号化されたままの状態で生体情報を確認することが期待されます。

3) ブロックチェイン分野

ブロックチェインの場合は、演算課程が全て把握可能という特性があり、個人情報は扱いにくいところがありましたが、同型暗号技術によって、ブロックチェインの活用分野がさらに広まると期待されてます。

6. OSS プロジェクト

現在、同型暗号に関して、さまざまなOSSプロジェクトが存在し、その中では有名な企業から展開しているものもあります。

例えば、GOOGLEで後悔しているOSSは、以下のgithubで参考できます。

そのほか、同型暗号OSSプロジェクトに関してまとめている、いいgithub repositoryがあるので、そこを記載しておきます。

後書き

同型暗号の概念はかなり難しのものですが、
筆者は実の所、同型暗号ということを知ったのは、最近となります。

ただ数年前、前職で、ウェブ上でキーボードを具現し、入力データが漏洩されないような仕組みを提案し、設計と開発・導入までして、特許をとるという経験があります。

その時思ったのは、「そもそも、暗号化はサーバーのみでやって、クライアントでは、暗号化されたままキー入力を処理し、そのままサーバーでもらって処理すれば、漏洩の危険は解消する」という考えから、提案と開発を主導してました。

しかし、その当時は同型暗号という概念はわからず、無理矢理の方法でそれを具現してましたが、最近同型暗号に関する資料をいろいろ見るうちに、「当時これを知っていたらな。。。」と苦笑いをしながら振り返るようになりました。

自分は現在も、決済周りの金融分野や、EC分野でもお金や個人情報を扱うサービスに関わるものとして、今後どこかで活用したいなと、強く思うようになりました。

まだまだ、学ばなければいけないものは山ほどですが、どこかで、導入し成功的に価値を生み出すようなことができればと思います。

※参考した資料

多くが韓国語なので、あんまり参考にならないかもですが、自分が参考した資料をまとめておきます。

● (英語) wikipedia
https://en.wikipedia.org/wiki/Homomorphic_encryption

● (日本語)　wikipedia 準同型暗号
https://ja.wikipedia.org/wiki/%E6%BA%96%E5%90%8C%E5%9E%8B%E6%9A%97%E5%8F%B7

● (韓国語) wikipedia
https://ko.wikipedia.org/wiki/%EB%8F%99%ED%98%95%EC%95%94%ED%98%B8#cite_note-OU98-2

● (韓国語) hashnet wiki
http://wiki.hash.kr/index.php/%EB%8F%99%ED%98%95%EC%95%94%ED%98%B8

● (韓国語) 同型暗号関連youtube
https://www.youtube.com/watch?v=v5tCivUh0lk

● (韓国語) comworld.co.kr記事
https://www.comworld.co.kr/news/articleView.html?idxno=49836

● (韓国語) LG CNS技術ブログ
https://blog.lgcns.com/2045?category=604440

● github oss repository
https://github.com/google/fully-homomorphic-encryption
https://github.com/jonaschn/awesome-he