LoginSignup
4
3

More than 1 year has passed since last update.

@gatosyocora(がとー しょこら)

ComputeShaderでテクスチャに線を描く

Posted at

はじめに

MeshDeleterWithTextureというテクスチャで塗った箇所に対応したMesh部分を削除するEditor拡張を作成しました。
このEditor拡張のメインの機能のひとつであるテクスチャを塗る際にComputeShaderを使用しているので、今回はこの部分の実装について記していきます。

ComputeShaderとは

Unityで計算用のGPUを使用するために使用されるシェーダーです。
一般的なシェーダーと同様のHLSLでプログラムを作成して、C#のプログラムからそれを実行します。
Unityで使用される一般的なシェーダー(vertex shader, fragment shader等)と異なる点は計算結果をC#のコードで利用できる点です。

コード全体

DrawExample.cs
public class DrawExample : ScriptableObject
{
    private ComputeShader computeShader;
    private int kernelId;

    private RenderTexture outputTexture;

    private Vector2Int previousPos;

    public void OnEnable()
    {
        computeShader = Instantiate(Resources.Load<ComputeShader>("drawCanvas"));
        kernelId = computeShader.FindKernel("CSPen");
    }

    // 初期化
    public void Initialize(RenderTexture outputTexture)
    {
        this.outputTexture = outputTexture;

        computeShader.SetInt("Width", outputTexture.width);
        computeShader.SetTexture(kernelId, "OutputTex", outputTexture);
        computeShaer.SetColor("PenColor", Color.Black);
        computeShader.SetInt("PenSize", 5);

        previousPos = new Vector2Int(-1, -1);
    }

    // OutputTextureにpreviousPosからposを繋ぐ線を描く
    public void Draw(Vector2Int pos)
    {
        // 終点
        var endPosArray = new int[2 * sizeof(int)];
        endPosArray[0 * sizeof(int)] = pos.x;
        endPosArray[1 * sizeof(int)] = pos.y;
        computeShader.SetInts("EndPos", endPosArray);

        // 始点
        var startPosArray = new int[2 * sizeof(int)];
        startPosArray[0 * sizeof(int)] = previousPos.x;
        startPosArray[1 * sizeof(int)] = previousPos.y;
        computeShader.SetInts("StartPos", startPosArray);

        previousPos = pos;

        // ComputeShaderを実行
        computeShader.Dispatch(kernelId, outputTexture.width / 32, outputTexture.height / 32, 1);
    }
}
drawCanvas.compute
#pragma kernel CSPen

RWTexture2D<float4> OutputTex;

int Width;
int StartPos[2];
int EndPos[2];

float4 PenColor;
int PenSize;

CGPROGRAM
// ABが上向きのベクトルかどうか
bool isUpwardVector(float2 a, float2 b) {
    return b.y - a.y > 0;
}

// ABが下向きのベクトルかどうか
bool isDownwardVector(float2 a, float2 b) {
    return b.y - a.y < 0;
}

// ABとCDが平行なベクトル関係か
bool isParallel(float2 a, float2 b, float2 c, float2 d) {
    float ab = (b.y - a.y) / (b.x - a.x);
    float cd = (d.y - c.y) / (d.x - c.x);
    return ab == cd;
}

// 外積
float mycross(float2 vec1, float2 vec2) {
    return vec1.x * vec2.y - vec1.y * vec2.x;
}

// ABとCDが交わっているか
bool isCrossLine(float2 a, float2 b, float2 c, float2 d) {
    return mycross(b - a, c - a) * mycross(b - a, d - a) <= 0 &&
        mycross(d - c, a - c) * mycross(d - c, b - c) <= 0;
}

bool isCountUp(float2 a, float2 b, float2 c, float2 d) {
    return !isParallel(a, b, c, d) && // 平行ならカウントしない
        isCrossLine(a, b, c, d) && // 交差するならカウントする
        ((isUpwardVector(a, b) && c.y != a.y) || // 上向きベクトルの始点と重なるならカウントしない
            (isDownwardVector(a, b) && c.y != b.y)); // 下向きベクトルの終点と重なるならカウントしない
}

// 太さlineSizeのABの線分上にpが載っているかどうか
bool isOnLine(float2 a, float2 b, float2 p, float lineSize, float width)
{
    // a,bを垂直方向に移動させた4点の長方形の中にあるかで判定する
    float2 q = float2(p.x + width, p.y);

    // ABに直交するベクトルを正規化
    float2 ab = a - b;
    float2 invAB = ab.yx;
    float2 normalizedInvAB = normalize(invAB);

    // a,bを垂直方向に移動させた4点
    float2 p1 = a + normalizedInvAB * float2(1, -1) * lineSize;
    float2 p2 = a + normalizedInvAB * float2(-1, 1) * lineSize;
    float2 p3 = b + normalizedInvAB * float2(-1, 1) * lineSize;
    float2 p4 = b + normalizedInvAB * float2(1, -1) * lineSize;

    int count = 0;
    if (isCountUp(p1, p2, p, q)) count++;
    if (isCountUp(p2, p3, p, q)) count++;
    if (isCountUp(p3, p4, p, q)) count++;
    if (isCountUp(p4, p1, p, q)) count++;

    return  fmod(count, 2) == 1;
}
ENDCG

[numthreads(32,32,1)]
void CSPen (uint2 id : SV_DispatchThreadID)
{
    int2 endPos = int2(EndPos[0], EndPos[1]);
        // endPosの場所に半径PenSizeの円を描く
    if (distance(endPos, id) <= PenSize) {
        OutputTex[id] = PenColor;
    }

    int2 startPos = int2(StartPos[0], StartsPos[1]);

        if (startPos[0] == -1) return;

    // startPosとendPosを繋いだPenSize*2の太さの線分上だったら塗る
    if (isOnLine(startPos.xy, endPos, id, PenSize, Width)) {
        OutputTex[id] = PenColor;
    }
}

実装の詳細

C#コード(ExampleDraw.cs)

OnEnableとInstanciateでComputeShaderを使うための初期化と前処理をしています。

    public void OnEnable()
    {
        computeShader = Instantiate(Resources.Load<ComputeShader>("drawCanvas"));
        kernelId = computeShader.FindKernel("CSPen");
    }

    // 初期化
    public void Initialize(RenderTexture outputTexture)
    {
        this.outputTexture = outputTexture;

        computeShader.SetInt("Width", outputTexture.width);
        computeShader.SetTexture(kernelId, "OutputTex", outputTexture);
        computeShaer.SetColor("PenColor", Color.Black);
        computeShader.SetInt("PenSize", 5);

        previousPos = new Vector2Int(-1, -1);
    }

ComputeShader#SetHoge(変数名, 値)でComputeShaderに値を渡します。
Width, OutputTex, PenColorとPenSizeは毎回の処理で変化しないので先に代入しておきます。

        computeShader.SetInt("Width", outputTexture.width);
        computeShader.SetTexture(kernelId, "OutputTex", outputTexture);
        computeShaer.SetColor("PenColor", Color.Black);
        computeShader.SetInt("PenSize", 5);

ExampleDraw＃Drawを呼び出すことで描画できるようにしています。

    public void Draw(Vector2Int pos)
    {
        // 終点
        var endPosArray = new int[2 * sizeof(int)];
        endPosArray[0 * sizeof(int)] = pos.x;
        endPosArray[1 * sizeof(int)] = pos.y;
        computeShader.SetInts("EndPos", endPosArray);

        // 始点
        var startPosArray = new int[2 * sizeof(int)];
        startPosArray[0 * sizeof(int)] = previousPos.x;
        startPosArray[1 * sizeof(int)] = previousPos.y;
        computeShader.SetInts("StartPos", startPosArray);

        previousPos = pos;

        // ComputeShaderを実行
        computeShader.Dispatch(kernelId, outputTexture.width / 32, outputTexture.height / 32, 1);
    }

描画する線の始点と終点をComputeShaderに渡します。

        // 終点
        var endPosArray = new int[2 * sizeof(int)];
        endPosArray[0 * sizeof(int)] = pos.x;
        endPosArray[1 * sizeof(int)] = pos.y;
        computeShader.SetInts("EndPos", endPosArray);

        // 始点
        var startPosArray = new int[2 * sizeof(int)];
        startPosArray[0 * sizeof(int)] = previousPos.x;
        startPosArray[1 * sizeof(int)] = previousPos.y;
        computeShader.SetInts("StartPos", startPosArray);

すべて値を設定終わったらComputeShaderを実行します。
textureの幅と高さを渡すことで、ComputeShaderは各ピクセルを並列に処理させています。

        computeShader.Dispatch(kernelId, outputTexture.width / 32, outputTexture.height / 32, 1);

ComputeShader(drawCanvas.compute)

CSPenがC#でComputeShaderを実行した際に実行される部分です。

[numthreads(32,32,1)]
void CSPen (uint2 id : SV_DispatchThreadID)
{
    int2 endPos = int2(EndPos[0], EndPos[1]);
        // endPosの場所に半径PenSizeの円を描く
    if (distance(endPos, id) <= PenSize) {
        OutputTex[id] = PenColor;
    }

    int2 startPos = int2(StartPos[0], StartsPos[1]);

        if (startPos[0] == -1) return;

    // startPosとendPosを繋いだPenSize*2の太さの線分上だったら塗る
    if (isOnLine(startPos.xy, endPos, id, PenSize, Width)) {
        OutputTex[id] = PenColor;
    }
}

まず、線の終点部分に半径PenSizeの円を描きます。
idに処理中のピクセル座標が入っているので、終点EndPosから半径PenSizeに含まれるピクセルならば塗ることで、
全ピクセルが処理されると、終点EndPosから半径PenSizeの円が描画されます。

    int2 endPos = int2(EndPos[0], EndPos[1]);
        // endPosの場所に半径PenSizeの円を描く
    if (distance(endPos, id) <= PenSize) {
        OutputTex[id] = PenColor;
    }

その後、始点から終点に太さPenSize*2の線を描きます。

    int2 startPos = int2(StartPos[0], StartsPos[1]);

        if (startPos[0] == -1) return;

    // startPosとendPosを繋いだPenSize*2の太さの線分上だったら塗る
    if (isOnLine(startPos.xy, endPos, id, PenSize, Width)) {
        OutputTex[id] = PenColor;
    }

書き始めは点のみなので前の点がなく、returnさせています。

if (startPos[0] == -1) return;

前回の処理によって、始点には半径PenSizeの円が書かれており、
前半の処理で終点には半径PenSizeの円が書かれているため、
線を描くためにはその円の間に長方形を描くとよいです。

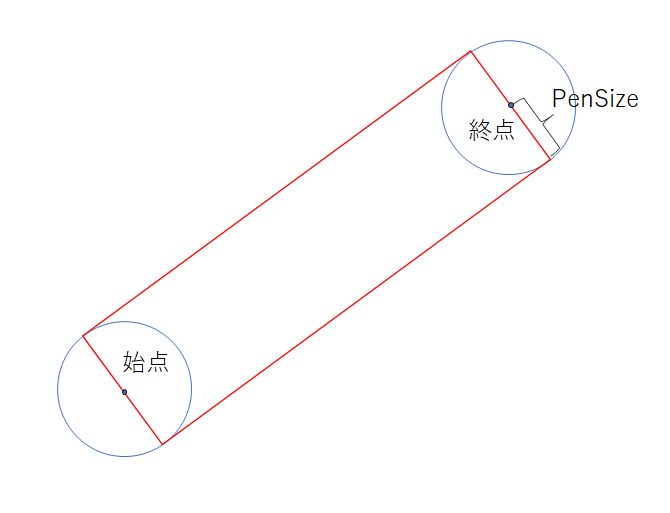
ComputeShaderでは各ピクセル視点で処理を書く必要があるので、
円の時と同様に各ピクセルはこの長方形の中に含まれるかで塗るか判断します。
isOnLineでこれを判断しています。

    if (isOnLine(startPos.xy, endPos, id, PenSize, Width)) {
        OutputTex[id] = PenColor;
    }

isOnLineは以下のような実装です。

bool isOnLine(float2 a, float2 b, float2 p, float lineSize, float width)
{
    // a,bを垂直方向に移動させた4点の長方形の中にあるかで判定する
    float2 q = float2(p.x + width, p.y);

    // ABに直交するベクトルを正規化
    float2 ab = a - b;
    float2 invAB = ab.yx;
    float2 normalizedInvAB = normalize(invAB);

    // a,bを垂直方向に移動させた4点
    float2 p1 = a + normalizedInvAB * float2(1, -1) * lineSize;
    float2 p2 = a + normalizedInvAB * float2(-1, 1) * lineSize;
    float2 p3 = b + normalizedInvAB * float2(-1, 1) * lineSize;
    float2 p4 = b + normalizedInvAB * float2(1, -1) * lineSize;

    int count = 0;
    if (isCountUp(p1, p2, p, q)) count++;
    if (isCountUp(p2, p3, p, q)) count++;
    if (isCountUp(p3, p4, p, q)) count++;
    if (isCountUp(p4, p1, p, q)) count++;

    return  fmod(count, 2) == 1;
}

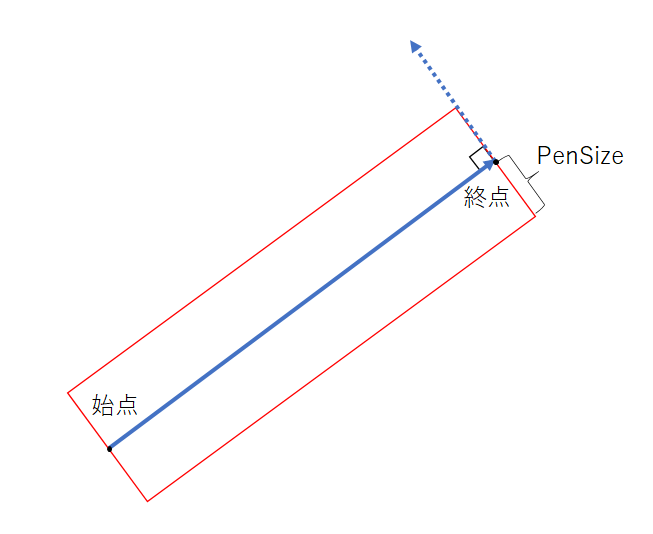
まず長方形の4点を求めます。
始点aと終点bを繋いだ線ABに対して、直交する方向にaとbを移動させると、この4点を求めることができます。

image.png

線AB(青い線)に直交する線（青い点線）は以下で計算します。
後で使いやすいように正規化もしています

    float2 ab = a - b; // 線ABベクトル
    float2 invAB = ab.yx; // 直交ベクトル
    float2 normalizedInvAB = normalize(invAB); // 正規化

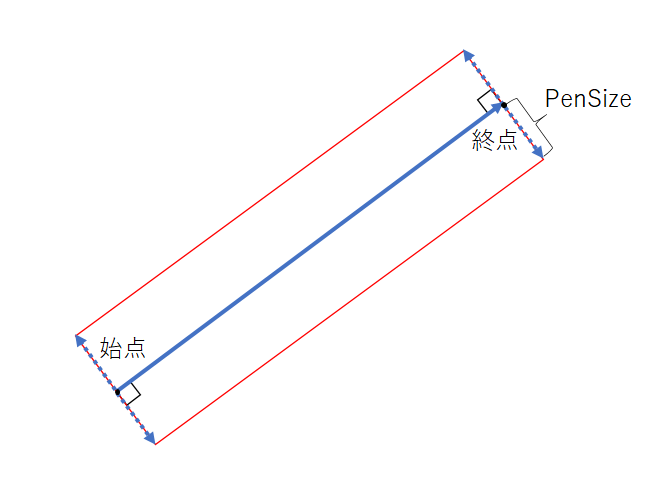
次に実際に4点を求めます。
直交ベクトルをa, bの各方向にPenSizeだけ移動させます。

image.png

    float2 p1 = a + normalizedInvAB * float2(1, -1) * lineSize;
    float2 p2 = a + normalizedInvAB * float2(-1, 1) * lineSize;
    float2 p3 = b + normalizedInvAB * float2(-1, 1) * lineSize;
    float2 p4 = b + normalizedInvAB * float2(1, -1) * lineSize;

これで長方形の4点p1, p2, p3, p4が求まりました。

あとは長方形に各ピクセルの点が含まれるかを求めます。
この判定にCrossing Number Algorithmを使用しました。
https://www.nttpc.co.jp/technology/number_algorithm.html

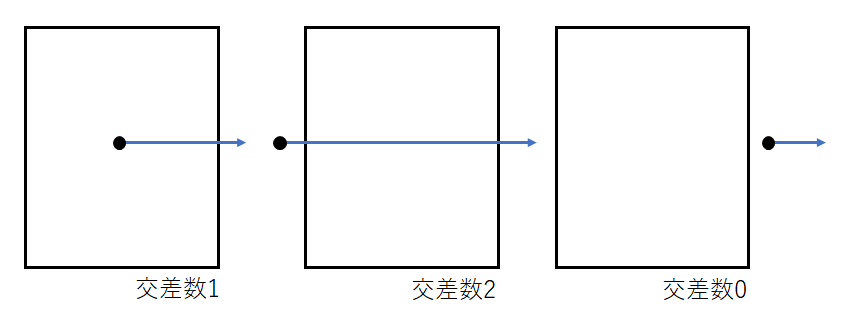
判定する点から端まで伸びる線と多角形の辺との交差回数が奇数なら点は内側にあるとするものです。

image.png

調べる点と繋ぐ点は確実に多角形の外にある必要があるので、Textureの幅(Width)分だけ水平方向に移動させた点qとしました。
調べる点pと平行移動させた点qの線が長方形の各辺と何回交差するか調べ、奇数ならtrueを返しました。

    float2 q = float2(p.x + width, p.y);

    ...

    int count = 0;
    if (isCountUp(p1, p2, p, q)) count++;
    if (isCountUp(p2, p3, p, q)) count++;
    if (isCountUp(p3, p4, p, q)) count++;
    if (isCountUp(p4, p1, p, q)) count++;

    return  fmod(count, 2) == 1;

交差しているかを調べるisCountUpは以下のようになっています。

bool isCountUp(float2 a, float2 b, float2 c, float2 d) {
    return !isParallel(a, b, c, d) && // 平行ならカウントしない
        isCrossLine(a, b, c, d) && // 交差するならカウントする
        ((isUpwardVector(a, b) && c.y != a.y) || // 上向きベクトルの始点と重なるならカウントしない
        (isDownwardVector(a, b) && c.y != b.y)); // 下向きベクトルの終点と重なるならカウントしない
}

以下をすべて満たす場合、交差していると判断しました。
精度をあげるために少し複雑になっています。
この条件はこの文献を参考にしました。
https://www.nttpc.co.jp/technology/number_algorithm.html

  • 線分abとcdが平行ではない(isParallel)
  • 線分abとcdが単純に交差している(isCrossLine)
  • 線分abが上向きのベクトルのとき、線分cdは始点aを通っていない(isUpwardVector && c.y != a.y)
  • 線分abが下向きのベクトルのとき、線分cdは終点bを通っていない(isDownwardVector && c.y != b.y)

各関数は以下のような実装になっています

// ABが上向きのベクトルかどうか
bool isUpwardVector(float2 a, float2 b) {
    return b.y - a.y > 0;
}

// ABが下向きのベクトルかどうか
bool isDownwardVector(float2 a, float2 b) {
    return b.y - a.y < 0;
}

// ABとCDが平行なベクトル関係か
bool isParallel(float2 a, float2 b, float2 c, float2 d) {
    float ab = (b.y - a.y) / (b.x - a.x);
    float cd = (d.y - c.y) / (d.x - c.x);
    return ab == cd;
}

// 外積
float mycross(float2 vec1, float2 vec2) {
    return vec1.x * vec2.y - vec1.y * vec2.x;
}

// ABとCDが交わっているか
bool isCrossLine(float2 a, float2 b, float2 c, float2 d) {
    return mycross(b - a, c - a) * mycross(b - a, d - a) <= 0 &&
        mycross(d - c, a - c) * mycross(d - c, b - c) <= 0;
}

上向きベクトル、下向きベクトルは点のy座標の差を見て求めています。

// ABが上向きのベクトルかどうか
bool isUpwardVector(float2 a, float2 b) {
    return b.y - a.y > 0;
}

// ABが下向きのベクトルかどうか
bool isDownwardVector(float2 a, float2 b) {
    return b.y - a.y < 0;
}

平行かどうかは各線の傾きが同じかどうかで求めています。

// ABとCDが平行なベクトル関係か
bool isParallel(float2 a, float2 b, float2 c, float2 d) {
    float ab = (b.y - a.y) / (b.x - a.x);
    float cd = (d.y - c.y) / (d.x - c.x);
    return ab == cd;
}

交差しているかは外積を使うことで計算できます。
HLSL標準の外積は2次元空間のものは計算できないので独自に作成したmycrossを使っています。

float mycross(float2 vec1, float2 vec2) {
    return vec1.x * vec2.y - vec1.y * vec2.x;
}

この外積の関係が以下のようなら交差すると判断できます。

    return mycross(b - a, c - a) * mycross(b - a, d - a) <= 0 &&
        mycross(d - c, a - c) * mycross(d - c, b - c) <= 0;

実際は < 0 で書かれていることが多いですが、

精度の関係かうまくいかないことがあったので <= 0 にしたところうまくいきました。

これらを満たすかどうかを計算することで各ピクセルが長方形に含まれるか計算でき、線を描くことができました。

参考

https://www.nttpc.co.jp/technology/number_algorithm.html
http://www.deqnotes.net/acmicpc/2d_geometry/lines

4
3
0

Register as a new user and use Qiita more conveniently

  1. You get articles that match your needs
  2. You can efficiently read back useful information
  3. You can use dark theme
What you can do with signing up
Sign upLogin
4
3