ゼロから作るDeepLearning第四章 ニューラルネットワークの学習

#-1　前回の振り返り
　前回は、ニューラルネットワークの概要について学習したのじゃ･･･
　ニューラルネットワークはパーセプトロンがたくさん繋がってできたもので、活性化関数を利用して非線形的に値を求めるんじゃったな･･･
　また、ニューラルネットワークの重みの計算では、線形代数の行列を使用して解くのじゃったな･･･
　線形代数は嫌いなのじゃ！

#0 第四章について
　第四章は、前回までで理解したニューラルネットワークの「学習」についてやっていくのじゃ･･･
　機械学習は、必要なパラメータ・特徴量を人間がある程度考える必要があったんじゃが、ディープラーニングではその作業も省略することが出来るのじゃ･･･
　ニューラルネットワークに、データを与えるだけで、自動で学習していくわけじゃな！
　今回は、その学習がどんな仕組みで行われているのかを見ていこうと思うのじゃ！
　･･･また、実装はあまりしないのじゃ!ライブラリを使えばあまり気にする必要がないからなのじゃ！でも、自分で全部書いて研究していきたいというひとは実装したほうがいいかもしれんのじゃ･･･

#1　ディープラーニングにおけるデータ
##1.1　機械学習との違い
　機械学習とディープラーニングの話をするとよく勘違いされることが多いのじゃが、機械学習とディープラーニングが全く別の物というわけではないのじゃ･･･
　というか機械学習のジャンルの手段の一つとしてディープラーニングがあるわけじゃな･･･

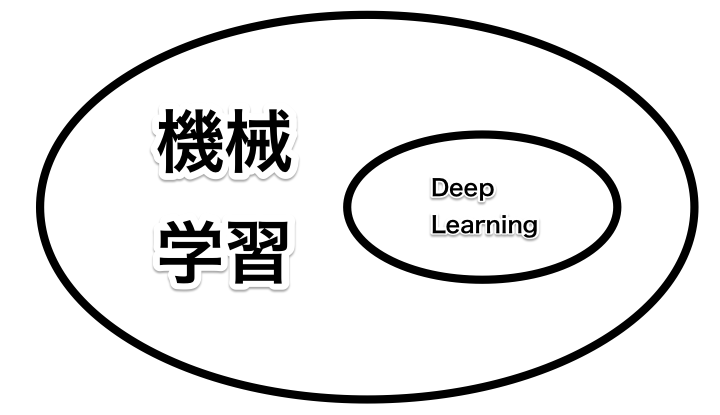
　じゃあ機械学習とディープラーニングの違いは何かと聞かれたら･･･
　一言で言うと**「ディープラーニングのほうが全自動で、最先端！」**じゃと妾は思っとる！
　どういうことかというと、機械学習では、パラメータの数や学習方法を自分で考える必要があるのじゃ･･･単純な内容ならデータの数も少なく、ある程度予想がつくため、機械学習を行うことも可能なのじゃ･･･
　でも、世の中そう簡単ではないのじゃ！複雑な内容を機械学習しようとすると、パラメータの数は指数関数的に増え、データの可視化も行えないため、どのように学習させればいいのか考えるのが非常に難しいのじゃ･･･
　･･･そこでディープラーニングの出番というわけじゃな！
　ディープラーニングは、データを与えるだけで、パラメータ・特徴量を自動で学習してくれるのじゃ！会社に例えると、何も言わなくても部下が何でもかんでも自分で考えて最高のパフォーマンスをしてくれるわけじゃな！
　ディープラーニング万歳！･･･というわけでもないのじゃ･･･
　ディープラーニングは全自動で学習するというメリットがあるというのは上で述べた通りなのじゃが、一方デメリットもあるわけじゃな･･･
　まず、計算量が機械学習よりも膨大なのじゃ･･･
　そして、ディープラーニングが勝手に学習して、データを分類できるようになったとしても、人間が理解できないというデメリットがあるのじゃ･･･
　ディープラーニングは膨大なパーセプトロンの組み合わせでできていて、パラメータの数も尋常なのじゃ･･･そのせいで、正しく分類できるようになったとしても、なぜ正しく分類できているかが人間にとっては理解できないらしいのじゃ！

##1.2　訓練データとテストデータ
　ディープラーニングは「正しいデータ」が命なのじゃ！
　正しいデータがたくさんあるということがディープラーニングにとって必須条件なのじゃな･･･

　ディープラーニングでは、データを取り扱う際に**「訓練データ」と「テストデータ」**の２つに分類して学習を行っていくのじゃ･･･

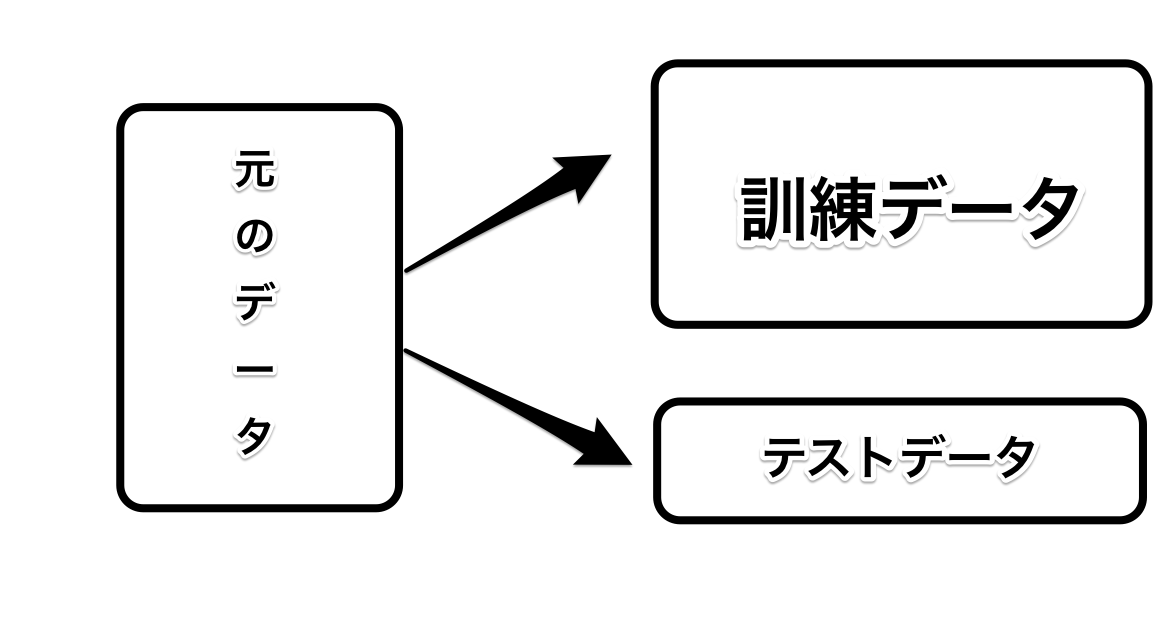
　目安で言うと訓練データが八割、テストデータが二割
が普通らしいのじゃ･･･

　･･･なぜデータをわざわざ２つにする必要があるのじゃ？　という疑問の声が聞こえたのじゃ
　なぜかというと、いろいろなデータに対応するできる汎化能力をニューラルネットワークに身に着けさせるためなのじゃ！
　訓練データで学習を行い、テストデータでどれぐらい正しく学習が行えているのか確認を行っていくのじゃ･･･そうしないと、与えられたデータに対してだけ完璧に対応してしまい、新しいデータに一切対応できなくなってしまうのじゃ！
　これを「過学習」というらしいのじゃ･･･

　データは訓練データとテストデータの２つにわけて、学習がきちんと行えているかテストを行うことが大切というわけじゃな！
　学校でいうと、訓練データが普通の授業！テストデータが定期テストみたいな感じじゃな！義務教育なのじゃ！

#2 損失関数
##2.1 損失関数とは
　ニューラルネットワークは勝手にニューラルネットワーク自身で学習を行っていくのじゃが、ただ闇雲に学習していては埒があかないのじゃ･･･
　ニューラルネットワークが何を基準にして学習をしていくのかは、人間が決める必要があるのじゃ･･･
　この学習の基準となるものが損失関数というものなのじゃ！
　名前の通り、損失・誤差についての関数を損失関数というのじゃ･･･
　損失関数はニューラルネットワークの性能の悪さの指標なのじゃ･･･現在のニューラルネットワークが訓練データに対してどれだけ適合していないか、一致していないのかを数値化したものなのじゃ！
　損失関数にはいろいろな種類があるのじゃ･･･早速見ていこうと思うのじゃ！

##2.2　二乗和誤差
　この二乗和誤差は、多分いちばん機械学習・ディープラーニングにおいてメジャー・簡単な損失関数なのじゃ！
　正しいデータと、ニューラルネットワークが予想したデータの誤差を二乗してすべて足したものなのじゃ･･･
　二乗する理由は、二乗してしまえば、マイナスの値も必ずプラスになるため、データどうしで打ち消し合うことを防いでいるというわけじゃな･･･

　数式でいうと以下のようになるのじゃ･･･

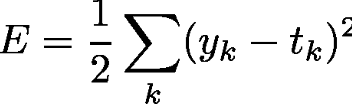
　y_kはニューラルネットワークの出力、t_kは訓練データで、kはデータの次元数を表すのじゃ･･･
　例えば、0~9の数の画像の認識の場合じゃと、kは１０となり、出力データと訓練データの誤差を求めるというわけじゃな･･･

　Pythonで実装すると以下のようになるのじゃ･･･

def mean_squared_error(y, t):
     return 0.5 * np.sum((y-t)**2)

##2.3 交差エントロピー誤差
　二乗和誤差の次に有名なのが、この交差エントロピー誤差じゃな･･･
　･･･エントロピーってなんだよという声が聞こえてきたのじゃ･･･
　エントロピーは、物理用語で、どれぐらい元のデータから予測できる値とかけ離れているかみたいなことらしいのじゃが、よくわからんのじゃ！

　数式で言うと以下のようになるのじゃ･･･
　
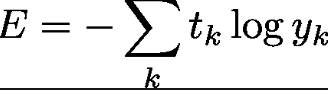
y_kはニューラルネットワークの出力、t_kは正解ラベルで、tには正解のラベルが1で、正解以外には0が入っているのじゃ（この表現をOne-hot表現というのじゃ）
　tは配列で[0,0,0,0,0,1,0,0,0]のように、正しいラベルの部分のみ1になっているのじゃ･･･
　よって、交差エントロピー誤差では、不正解のラベルの部分は、tの値が0のため、計算結果がゼロになり、実質正解ラベルとの計算結果のみが求められるというわけじゃな･･･
　二乗和誤差よりも、正解ラベルと出力結果の答えが異なるとき誤差が極端に大きくなるということが特徴的なのじゃ･･･

　Pythonで実装すると以下のようになるのじゃ･･･

def cross_entropy_error(y, t):
    delta = 1e-7
    return -np.sum(t * np.log(y + delta))

deltaは無限大に発散することを防ぐための防止策なのじゃ･･･

#3.ミニバッチ学習
　ディープラーニングでは、データを利用して学習を行うのじゃが、だいたいの場合、データの数は数万・数百万など、尋常じゃない数になってしまうのじゃ･･･
　というかそんぐらいないと、汎用的なニューラルネットワークにならないらしいのじゃ･･･
　
　莫大なデータを学習する際に、すべてのデータに対して学習しているのはいくら時間があっても終了しないのじゃ･･･
　そこで、全体の中からデータを一部取り出して、取り出したミニバッチごとに学習をおこなっていくことをミニバッチ学習というのじゃ･･･
　メリットとしては、計算量を減らすことができたり、毎回取り出すデータが異なるため、偏ったニューラルネットワークになってしまうことを防ぐことが出来るというめりっとがあるのじゃ･･･

#4 微分と勾配
　ニューラルネットワークは、損失関数の値を減らすことが最大の目的なのじゃ･･･
　なぜかといいうと、損失関数の値が大きいと、それだけニューラルネットワークは正しい値を出力できていないという意味になるからなのじゃ･･･
　逆に言うと、損失関数の値を減らすことができれば、ニューラルネットワークはどんどん正しいモデルになってきているということを表すのじゃ･･･

　損失関数の値を減らすためには、高校数学でやった微分を利用するのじゃ･･･
　微分は、xが微小量変化する際に、yがどれだけ変化するのかをあらわすのじゃ･･･
　微分を利用すると、xがほんの少し増えるとyがどれだけ増加するかを求めることができ、それを逆向きにすると、損失関数をどんどん減らすことができるのじゃ･･･
　この内容はCouseraのMachineLearningのコースがすごくわかりやすいのじゃ･･･！

　勾配は、この微分を、各パラメータと損失関数の組み合わせで行って、ベクトルとして格納したものなのじゃ･･･
　勾配のベクトルの指す方向は、損失関数の極小値の方向で、勾配のベクトルだけパラメータを更新していくと、損失関数がどんどん小さくなっていくのじゃ･･･
　ちなみに一回の更新の大きさは学習率というのじゃ･･･
　このように勾配を利用して、どんどん損失関数を減らしていく方法を勾配降下法といい、機械学習においてもメジャーな方法なのじゃ･･･

#5 学習アルゴリズムの流れ
##5.1 用語
　ニューラルネットワークの学習に大切な用語はこれまで見てきた

• one-hot表現
• 損失関数
• ミニバッチ
• 微分・勾配
• 学習率
• 勾配降下法

　などがあるのじゃ･･･

##5.2　学習の流れ

　ニューラルネットワークの学習は以下のような手順で行うのじゃ･･･

1. 学習データの中からランダムにデータを取り出す。このデータセットをミニバッチという。
2. ミニバッチの値をニューラルネットワークに流し込む。ニューラルネットワークから値が吐き出され、これは損失関数の値と呼ばれる。
3. 損失関数の値を利用して、各重みパラメータに対する勾配を求める。ここで求めた勾配は、損失関数の値を減らす方向を示している。
4. 重みパラメータを勾配×学習率の分だけ更新する。こうすることで損失関数の値は小さくなる。
5. ステップ1~4を、予め決めた基準を満たすまで繰り返す。

　上のような手順でニューラルネットワークの学習を行っていくのじゃ･･･
　最初は難しいかもしれんが少しずつ体に馴染んでくるのじゃ･･･
　
　ちなみに、ステップ5の後に、テストデータでどれ位正しく学習できているかを調べることがあるのじゃ･･･
　そうしないと、偏った学習を永遠と続けてしまう可能性があるからなのじゃ･･･

#6　振り返り
　駆け足でニューラルネットワークの学習についてみてきたのじゃ･･･
　やっぱりニューラルネットワークは難しく、それでいて奥が深いと改めて感じたのじゃ･･･
　もうちょっとニューラルネットワークのテストの精度について理解しないといけないと感じたのじゃ･･･

#7　それぞれの章へのリンク
・自分流まとめホーム
・第二章 パーセプトロン
・第三章 ニューラルネットワークの学習
・第四章 ニューラルネットワークの学習
・第五章 誤差逆伝播法
・第六章 学習においてのテクニック
・第七章 畳み込みネットワーク
・第八章 DeepLearning

#8 参考文献
　書籍　ゼロから作るDeepLearning　オライリー・ジャパン
Qiitaの数式チートシート
https://qiita.com/PlanetMeron/items/63ac58898541cbe81ada