Kokkosで始める並列プログラミング入門【CPU/GPU】

はじめに

「GPUプログラミングに興味があるけれど、CUDAは難しそうだし書きたくない……」
「ある並列プログラムをCPUとGPUで性能比較したいけれど、それぞれに対してコードを書くのは面倒……」

そういう方におすすめしたいのが、Kokkosという並列計算のためのC++ライブラリです。
このライブラリが持つ大きな特徴としては、高い performance portablity を有していることにあります。つまり、あるプログラムを、コードを変えず、性能を保ったまま異なる環境で動かすことができるということです。
Kokkosは、OpenMP、CUDA、SYCL、HIPなどのさまざまなバックエンド環境をサポートしており、これらを高い抽象度で記述することができます。

本記事では、並列プログラミングに関する前提知識をおさらいしたうえで、Kokkosの基本事項を学び、簡単な使用例を解説しようと思います。

必要な知識

• C++の基本文法
• ターミナルの使い方

あるとよい知識

• C++の応用的な文法（ラムダ式など）
• 並列計算に関する基本事項
  • CUDAやOpenMP
  • データ並列性、GPUの構造、スレッドのしくみ、並列アルゴリズム
• Git, CMake, Docker, VSCodeの使い方

この記事を読んでほしい人

• C++やったことあるよという人
• とりあえずGPUを使ってみたい、並列処理に触れてみたい人
• Kokkosについて軽く知りたい人

あまりおすすめしない人

• Kokkosの詳細な仕様やビルド方法を知りたい人
  • ビルドについてはほぼ立ち入らず、「とりあえず動かしてみる」を重視した記事です

並列プログラミングに関する基本事項

もう知っているという方は飛ばして結構です。

並列計算のしくみ

コンピュータが並列に計算を行うとき、内部ではどのような処理が行われているのでしょうか。

プログラムは スレッド という処理の単位で実行されます。わわわIT用語辞典さんの説明が直感的でわかりやすいです。スレッドはCPUが複数持っている コア で実行され、通常1コアあたり1スレッドを処理できます。

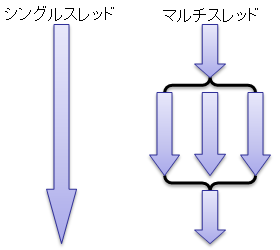
通常のプログラムでは、一つのスレッドが上から順番にプログラムを計算していきます。この実行の形式を シングルスレッド といって、これは 逐次 的な実行方法です。

反対に、ある処理を複数のCPUコアが複数のスレッドによって同時に計算する形式のことを マルチスレッド といい、 これは 並列 的な実行方法です。
プログラムをうまく並列化することで、短い時間で実行できたり、同じ時間でより多くの計算を行うことができます。

プロセスが並列処理をする部分に差しかかると、プログラムは新たにスレッドを複数個生成します。そして、並列処理の部分が終わると、先ほど生成されたスレッドは終了され、元のスレッド（メインスレッド）のみが残ります。

(https://ufcpp.net/study/csharp/sp_thread.html)

並列プログラミングの注意点

並列プログラミングには、逐次プログラミングにはなかった難しさが現れてきます。その例を二つほど覚えておきましょう。
Kokkosを使う際にも必要になる知識です。

データの競合

各スレッドは変数を共有したり、ローカルな変数を持ったりすることができます。このうち、共有している変数の扱いに関して、特に取り扱いを気を付ける必要があります。

例えば、スレッドから共有している変数に同時に書き込みを行った場合はどうなるでしょうか。これは レースコンディション（競合状態） という状態です。共有しているデータに対する処理がスレッド間で競合すると、その実行順序によって結果が不定になってしまうため、これを発生させないよう意識する必要があります。

よくある例として、変数aを用意して、インクリメントすることを考えましょう。初期値は1とします。変数が更新されるまでに、コンピュータの内部で命令が分割され、以下の二つの処理が実行されるでしょう。

1. aの読み取り(1が読みこまれる)
2. インクリメントの結果を格納(aに2が格納される)

では、aを二つのスレッドX,Yで共有し、二回のインクリメントを行うケースを考えてみましょう。最終的にaには3が代入されてほしいです。しかし、各スレッド間での実行順序に制限を課さない場合、以下のように交互に操作が行われるケースが起こりえます。

1. Xがaを読みとり(1が読みこまれる)
2. Yがaを読みとり(1が読みこまれる)
3. Xがインクリメントの結果を格納(aに2が格納される)
4. Yがインクリメントの結果を格納(aに2が格納される)

二つの処理が衝突した結果、誤って2が格納されてしまいました。

この例における、読み取りから格納までの操作のように、別の処理が割り込まれてはいけない一連の操作を クリティカルセクション と呼びます。クリティカルセクションの競合を避けるためには、プログラマがアルゴリズムを変更するか、排他制御 を採用する必要があります。

排他制御とは、共有されたデータを同時に操作できるスレッドの数を制限する方法のことです。これを実現する主な方法としては、セマフォ （現在利用可能なリソースの数を表す値）などを利用するか、アーキテクチャに命令単位で組み込まれている アトミック操作 を用いるか、データレプリケーション （各スレッドが独自のデータコピーを持ち、最終的にデータを統合する方法）を行うの三つの方法があります。の三つの方法があります。

同期の必要性

長さ$N$の二つの配列$A$と$B$があり、$B$の各要素に$A$の各要素をそれぞれ加算する、という操作を並列に行います。その後、$B$の要素の総和を reduction によって取得するケースを考えましょう。

まず、各スレッドが$B$への加算を並列に行うなかで、メインスレッドの処理が早く終わったとします。メインスレッドがそのまま他のスレッドの処理の完了を待たないで先の処理を進めてしまうと、$B$が完全に更新されなまま、reduction が始まってしまいます。そうなれば、当然この処理の結果は本来の値とは異なってしまいます。

これを防ぐために、並列処理の終わりの部分には バリア というものを置いて、すべてのスレッドの完了を待つ必要があります。これを （バリア）同期 といいます。

並列化に適した問題とは

さて、プログラムを並列に動かすためには、そのデータやアルゴリズムが並列処理に適した構造/サイズであることが必要です。どのような問題に対して並列化が適していて、あるいは適していないのか、いくつか具体例を通して見ていきます。

---

問1.
整数値の配列があります。配列の長さは $10^7$ です。この配列の各要素に $1$ を足してください。

これは並列処理に適しています。なぜなら、「各要素に1を足す」という操作は要素ごとに依存関係がないためです。
各要素への操作を異なるスレッドに割り当てることで、全体の計算をマルチスレッドで並行して実行することができます。
このような独立なデータに対するシンプルな並列化は、Embarrassingly parallel といって、「バカパラ」とか訳します。（馬鹿でもできるためです。）

---

問2.
整数値の配列があります。配列の長さは $100$ です。この配列の各要素に $1$ を足してください。

これは（実用上）並列処理に適していません。各要素への操作は独立ですが、問題のサイズが小さすぎるためです。
スレッドの作成にはオーバーヘッドがかかります。大規模なデータに対する操作や計算量の多い問題では、並列処理が有効である一方、計算のコストが小さいことが決まっている簡単な問題では、処理全体に占める時間のうち、オーバーヘッドが優位になってしまい、逆にパフォーマンスが低下する可能性があります。
GPUを利用する際は、データの転送コストも考慮する必要があります。

ここの塩梅は、実際に計測するか、経験的に予測して調整するしかありません。

---

問3.
整数値の配列があります。配列の長さは $N$ です。フィボナッチ数の第 $i$ 項を計算し、それぞれ $A[i]$ に格納してください。（ただし、一般項を計算するのは禁止します。）

これは並列処理に適していません。$A[i] = A[i - 1] + A[i - 2]$ と表されることから、$A[i]$ は他の要素の計算結果に依存していることがわかります。したがって、逐次的に計算していくしかありません。
このように、計算の順序が決められている問題は、アルゴリズムを変更しない限り並列化できません。

---

問4.
整数値の配列があります。配列の長さは $N$ です。この配列のすべての要素の和を計算してください。

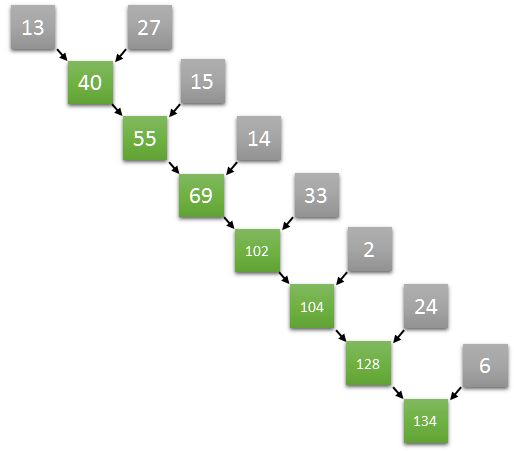
逐次プログラムで単純にこれをやると、前から順番に $N-1$ 回の加算を行うことが必要です。以下の画像は、加算の関係を二分木で表した図です。この木の深さが加算の回数、すなわち実行のコストに相当します。

(https://eximia.co/implementing-parallel-reduction-in-cuda/)

これをどうにか並列化できないか考えます。少なくともバカパラによって解決しようとするのは困難そうです。

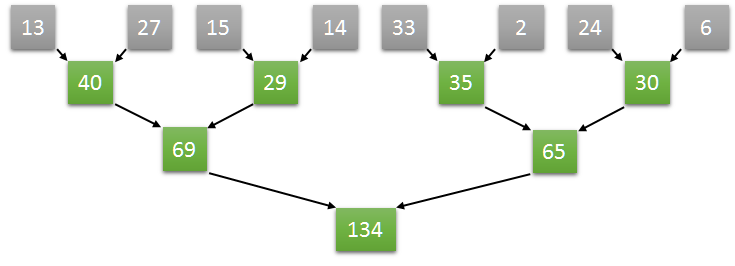
ここで少し工夫をして、以下の図のように平衡な二分木のように足し算を行うことを考えてみます。すると、二分木の同じ階層にある加算はそれぞれ独立な操作として処理できるため、うまく並列化することができ、木の深さを $O(logN)$ まで抑えることができました。

$P$ 個のスレッドを同時実行できるモデルを仮定するとき、計算量は $O(\frac{N}{P} + logN)$ です。
$P=O(\frac{N}{logN})$ とするのが最適らしいです（Brent’s theorem）。
(https://developer.download.nvidia.com/assets/cuda/files/reduction.pdf/ 29-30ページ)

このようにして二項演算の集約を並列化する手法を reduction と呼びます。

(https://eximia.co/implementing-parallel-reduction-in-cuda/)

この例のように、アルゴリズムを変更することで並列化がうまくいくパターンがいくつかあります。

Kokkosを使ってみる

並列処理に関する基本事項を身に着けたところで、Kokkosを使ってみましょう。

Kokkosの利用環境を整えたリポジトリを用意しました。VSCodeでの利用と、NVIDIA製のGPUが利用可能であることを想定しています。利用しているGPUがRTX30シリーズでない場合は、本記事の付録を参照し、リポジトリのビルドオプションを適切に変更してください。

まず、NVIDIA公式サイトから、GPUのドライバをダウンロードしてください。

次に、ターミナルから以下のコマンドを実行してリポジトリをダウンロードします。

git clone --recurse-submodules https://github.com/gandalfr-KY/kokkos-workspace

ダウンロードができたら、VSCode上でこのフォルダを開き、Dockerコンテナを起動してください。
VSCode上でDockerを使う方法については、以下の記事を参考にしてください。

これができれば設定は完了です。

以下のコマンドを実行すると、OpenMPのみを利用できる環境でコンパイルされます。本記事ではこの環境をCPU環境と呼びます。

-gオプションを付けて実行すると、OpenMP+CUDAをバックエンドとして利用できる環境でmain.cppがコンパイルされます。本記事ではこの環境をGPU環境と呼びます。

-sオプションをつけるとCPUによる逐次実行のみの環境になります。

./scripts/build.sh

実行ファイルはbuild/下にmainとして生成されます。

initialize, finalize

Kokkosのデータ構造を使う際には、必ずKokkos::initializeを、終了時にはKokkos::finalizeを呼ぶ必要があります。
finalizeを呼ぶ前にはすべてのKokkosのデータ構造がデストラクトされている必要があるため、main関数の中にブロックをもう一階層追加して、処理を書き始めるとよいでしょう。

#include <Kokkos_Core.hpp> // 基本的な関数はすべてこれに入っている

using namespace Kokkos;

int main() {
initialize(); // Kokkosのデータ構造を使う際、最初に必ず呼ばなければならない関数
{
    
    // 処理

}
finalize(); // Kokkosのデータ構造を使う際、最後に必ず呼ばなければならない関数
}

View

Kokkosの核をなすのが、Kokkos::Viewという配列のような役割をするデータ構造です。通常の配列と異なる点は、 ホスト（≒CPU）と デバイス （≒GPU）のメモリのどちらにも確保できるという点です。

以下は、長さがNのViewを確保する例です。Viewのテンプレート引数には、要素の型と、その他のプロパティを渡します。要素の型に付けた*の数は配列の次元を表します。ViewのViewを作成する必要はありません。

プロパティでは、確保するメモリの属性や、多次元配列の レイアウト、メモリ管理の仕方などを指定できます。

例えばホストの環境を意味するKokkos::HostSpaceをプロパティに渡すと、ホストメモリ上にViewのデータを確保します。何も指定しない場合、CPU環境でコンパイルされるとホストメモリに、GPU環境ではデバイスメモリに確保 されます。

レイアウトというのは、多次元配列をメモリ上に並べ直すときの順番のことです。指定しない場合は、ホストに確保されている場合LayoutRight（行優先）に、デバイスに確保されている場合はLayoutLeft（列優先）に自動的に設定されます。意味がよく分からない方はWikipediaを参照してください。どうしてこのような仕様になっているかというと、ホストとデバイスでキャッシュに乗りやすいアクセスパターンが異なるためです。本記事では深く立ち入りません。

コンストラクタの引数には、ラベル（変数名のようなもの）と確保するサイズを指定します。

#include <Kokkos_Core.hpp>

using namespace Kokkos;

int main() {
initialize(); // Kokkosのデータ構造を使う際、最初に必ず呼ばなければならない関数
{
    
    const int N = 1000, M = 500;
    View<int*, HostSpace> h_array("host_array", N); // cpuからアクセス可
    View<int*, CudaSpace> d_array("device_array", N); // gpuからアクセス可, gpu環境のみコンパイル可
    View<int*> array("auto_array", N); // ビルド環境に合わせて自動的に選択してくれる

    View<double**> matrix("matrix", N, M); // ≒ double[N][M]
    View<double**, LayoutLeft> matrix_fortran("matrix", N, M); // 列優先の2次元配列
    View<double**, LayoutRight> matrix_c("matrix", N, M); // 行優先の2次元配列

}
finalize(); // Kokkosのデータ構造を使う際、最後に必ず呼ばなければならない関数
}

---

データにアクセスする場合は、通常の配列のときのような角括弧を使うのではなく、丸括弧とカンマで表記します。
注意する点としては、ホストからデバイス、またはデバイスからホストのデータにアクセスしてはいけないということです。アドレス空間が異なるために実行時エラーを引き起こし、プログラムが終了します。デバイスのデータへのアクセスの方法は後述します。

#include <Kokkos_Core.hpp>

using namespace Kokkos;

int main() {
initialize();
{
    
    const int N = 1000, M = 500;
    View<int*, HostSpace> h_array("host_array", N);
    View<int**, HostSpace> h_matrix("host_matrix", N, M);
    int a = h_array(4); // <=> h_array[4]
    int b = h_matrix(3, 5); // <=> h_matrix[3][5]

    View<int*, CudaSpace> d_array("device_array", N);
    int c = d_array(4); // これは間違い！

}
finalize();
}

---

また、Viewのコピーは シャローコピー です。std::vectorなどのデータ構造のように、要素をひとつずつコピーしていくのではなく、データのアドレスを共有します。
Viewは内部にstd::shared_ptrのような参照カウンタを持っていて、それを参照している変数が存在しなくなったときにデストラクトされます。

#include <Kokkos_Core.hpp>

using namespace Kokkos;

int main() {
initialize();
{
    
    const int N = 1000;
    View<int*> array1("host_array", N);
    View<int**> array2;

    array2 = array1;

    // array1とarray2は全く同じデータを参照している！

}
finalize();
}

---

なお、KokkosではCudaSpaceなど特定のデバイスに関するプロパティを指定するのはあまり推奨しません。Kokkosが謳う performance portability を保つためには、環境を変えてもコンパイルできるコードを書くことが重要です。CudaSpaceはCPU環境では使えませんので、その代わりに、メモリスペースを指定しないか、DefaultExecutionSpace（CPU環境ではOpenMP、GPU環境ではCudaとしてコンパイルされる）などの自動で切り替わるキーワードを使い、より汎用性の高い書き方を使用することが望ましいと思います。

parallel_for

Viewと並んで最もよく使う関数が、Kokkos::parallel_forです。名前の通り、並列にループ処理をする関数です。

parallel_forは、第一引数にループの回数、第二引数に ファンクタ を取ります。ファンクタというのは、関数のように振る舞うことができるオブジェクトのことです。Kokkosでは以下のようにKOKKOS_LAMBDAを使った書き方をします。

ファンクタには、0以上loop_limit未満のループ変数iに対して、並列に動作する処理を記述します。ここに記述した処理は、CPU環境ならホストで、GPU環境ならデバイスで 並列実行されます。

Kokkos::parallel_for(
    loop_limit, // ループする回数
    KOKKOS_LAMBDA(int i) { // 各i(0<=i<loop_limit)について 
        // 並列にやりたい処理
    }
);

KOKKOS_LAMBDAは、CPU環境では[=]、GPU環境では[=] __host__ __device__に展開されるマクロです。C++に慣れた方ならもうお分かりと思いますが、KOKKOS_LAMBDA(int i) {}という部分は、結局コピーキャプチャのラムダ式に等しいわけです。

__host__ __device__の部分は関数型修飾子というCUDAの拡張構文で、その関数を呼び出す環境を指定するためのキーワードです。関数型修飾子については、Kokkosを使う上では、以下の四つの効果を覚えておけば十分です。

1. __host__をつけた関数は、ホスト上で実行するためにコンパイルされる
2. __device__をつけた関数は、デバイス上で実行するためにコンパイルされる
3. __host__ __device__をつけた関数は、どちらでも実行できるようコンパイルされる
4. 以上二つの関数型修飾子をどちらも付けない場合、__host__属性の関数として解釈される

---

コードがホストとデバイスのどちらで実行されているかを意識しながらプログラミングをしましょう。先述したように、デバイスのデータにはデバイスからしかアクセスできないので、デバイス側に確保したViewには、必ずparallel_for内からアクセスするようにしましょう。
同様に、ホストのデータやホスト用の関数にはホストからしかアクセスできないので、parallel_for内でstd::vectorなどのデータ構造にアクセスしてはいけませし、std下に定義されている関数も呼ぶことができません。

#include <Kokkos_Core.hpp>

using namespace Kokkos;

int main() {
initialize();
{

    const int N = 1000;
    View<int*, CudaSpace> array("array", N);
    std::vector<int> h_vector(N);
    
    parallel_for(N, KOKKOS_LAMBDA(int i) {
        array(i) = i * 2 + 1;        // OK (デバイス上のデータへのアクセス)
        h_vector[i] = i * 2 + 1;     // NG (ホストメモリへの直接のアクセスは不可)
        std::cout << i << std::endl; // NG (ホスト関数の呼び出しは不可)
    });
    fence(); // 後述

}
finalize();
}

ちなみに、デバイスでも使える関数を定義するには、KOKKOS_FUNCTIONとか、KOKKOS_INLINE_FUNCTIONを関数の定義の頭に付けます。KOKKOS_FUNCTIONは、CPU環境なら空、GPU環境なら__host__ __device__に展開されます。KOKKOS_INLINE_FUNCTIONはこの後ろにinlineが付いたものです。

KOKKOS_INLINE_FUNCTION void func(int a) {
    return a + 1;
}

---

多重ループの際は、以下のように書きます。少し複雑ですが、慣れれば大丈夫でしょう。
MDRangePolicyというクラスを渡すことで複数の変数の始点と終点を渡します。テンプレート引数として、Rankによって制御変数の数を指定する必要があります。
ファンクタの変数は、Rankで渡した数と同じだけの変数を用意しましょう。

#include <Kokkos_Core.hpp>

using namespace Kokkos;

int main() {
initialize();
{

    const int N = 1000, M = 500;
    View<int**> matrix("matrix", N, M);
    
    parallel_for(
        MDRangePolicy<Rank<2>>({0, 0}, {N, M}), 
        KOKKOS_LAMBDA(int i, int j) { // 各i: [0, N), 各j: [0, M) についての処理
            matrix(i, j) = i * M + j;
        }
    );
    fence(); // 後述

}
finalize();
}

parallel_reduce

前章の最後の問題で紹介した reduction の手法を、Kokkos::parallel_reduceから使うことができます。

parallel_reduceは、第一引数にループの回数、第二引数にファンクタ、第三引数に集約結果を格納する変数を取ります。ファンクタの形式はparallel_reduceと似ていますが、値をスレッドごとに保持するための変数のアドレスも持つ必要があります。この変数の値を第三引数に集約します。

以下に、配列内のすべての要素の合計を計算する例を示します。

#include <Kokkos_Core.hpp>

using namespace Kokkos;

int main() {
initialize();
{

    const int N = 10;
    Kokkos::View<int*> array("array", N);
    parallel_for(N, KOKKOS_LAMBDA(int i) { array(i) = i * i; });

    int sum;
    parallel_reduce(N, KOKKOS_LAMBDA(int i, int& local_sum) {
        local_sum += array(i);
    }, sum);

}
finalize();
}

---

reduction は総和を取る関数であると説明しましたが、これはもっと抽象化することができましょう。この和を取るという操作は、別の操作に置き換えることができそうですね。
この操作が満たすべき性質は、モノイド に属する二項演算であることです。モノイドは、以下の性質を持つ代数的構造です。

• 集合$S$に対して、$S \times S \rightarrow S$を満たす
• どのように括弧をつけても同じ結果になる（結合律）（例：$(1+2)+3=1+(2+3)$）
• 演算しても結果が変わらない要素が存在（単位元の存在）（例：$3+0=3$）

ただしKokkosでは、モノイドよりももう少し狭いクラスである、可換モノイド であるよう要請されます。モノイドに以下の条件を加えた演算が可換モノイドに属します。

• 可換則：項を入れ替えても結果が変わらない（例：$1+2=2+1$）

例えば、加算や乗算、最小公倍数、最大公約数、max、min、and、or、xorなどの演算がこれを満たします。

いくつかの代表的な演算はあらかじめKokkosで用意されており、第三引数を以下のようにラップされた形で渡すことで使うことができます。一覧は公式ドキュメントに記載されています。

#include <Kokkos_Core.hpp>

using namespace Kokkos;

int main() {
initialize();
{

    const int N = 100;
    double prod;
    parallel_reduce(N, KOKKOS_LAMBDA(int i, int& local_prod) {
        local_prod *= i;
    }, Prod<double>(product)); // 総積を取る

}
finalize();
}

自分で演算をカスタムするは、ファンクタのためのクラスを作成し、二項演算に相当するjoinメソッドと、単位元に相当するinitメソッドを定義することで可能です。詳しくは公式ドキュメントを参照してください。

parallel_scan

累積和配列とは、入力の配列の各位置に対して、先頭からその位置までの全要素の和を計算した配列です。例えば、[1, 2, 3]に対する[1, 1+2, 1+2+3]が累積和配列です。これを並列に構築するのは一見すると困難そうですが、驚くべきことに、これを並列に構築するアルゴリズムが存在しています（Blelloch Algorithm）。Kokkosはこれを簡潔に記述できます。

Kokkos::parallel_scanは、半群 （$S \times S \rightarrow S$の演算で、結合律を持つ演算）に属する二項演算において、各スレッドに対応する累積値を求める関数です。（parallel_reduceと違って可換則について言及されていませんでした。自信がないです……。）
parallel_reduceと同様、デフォルトでは加法が設定されており、演算のカスタムもjoinとinitを定義したクラスを定義することで実現できます。

ファンクタの形式は、parallel_reduceのものに新たにフラグを追加した形になります。ファンクタは各スレッドで複数回呼び出されることがあり、このフラグは「最後の呼び出しであるかどうか」を持っており、このフラグが真であるとき、集約している値が累積値としての最終結果であることを意味します。

#include <Kokkos_Core.hpp>

using namespace Kokkos;

int main() {
initialize();
{
    const int N = 10;
    View<int*> output("output", N);
    parallel_scan(N, KOKKOS_LAMBDA(int i, int& update, bool is_final) {
        update += (i + 1);
        if (is_final) {
            output(i) = update; // is_finalがtrueであれば、updateは累積値として最終結果になっている
        }
    });
    // output: [1, 3, 6, 10, ...]

}
finalize();
}

deep_copy

Viewはシャローコピーであるという説明をしました。ディープコピー（同じアドレスを共有しないコピー）をしたいときには、Kokkos::deep_copyという関数を使います。この関数では、違うメモリスペース間でのコピーも可能です。

例えばデバイスのデータを出力したいときは、一度ホストにコピーしてからforでループさせればよいです。

#include <iostream>
#include <Kokkos_Core.hpp>

using namespace Kokkos;

int main() {
Kokkos::initialize();
{
    const int N = 10;
    Kokkos::View<int*> array("device_array", N);
    Kokkos::View<int*, HostSpace> h_array("host_array", N);
    deep_copy(h_array, array); // h_array = array;
    for (int i = 0; i < N; ++i) {
        std::cout << h_array(i) << std::endl; // ホストからアクセス可能
    }

}
Kokkos::finalize();
}

注意点として、異なるレイアウトのViewはコピーできません。

#include <iostream>
#include <Kokkos_Core.hpp>

using namespace Kokkos;

int main() {
Kokkos::initialize();
{

    const int N = 10;
    Kokkos::View<int**> matrix_left("device_matrix_layout_left", N, N);
    Kokkos::View<int**, LayoutRight> matrix_right("device_matrix_layout_right", N, N);
    Kokkos::View<int**, HostSpace> h_matrix("host_matrix", N, N);
    deep_copy(h_matrix, matrix_left);  // ホストとデバイスでレイアウトが異なるので、エラー
    deep_copy(h_matrix, matrix_right); // レイアウトが一致しているので、OK

}
Kokkos::finalize();
}

fence

Kokkos::fenceは、前章で触れた、バリア同期 を行う関数です。

Kokkosにおける非同期的な（＝すべてのスレッドの処理の終了を待たない）関数は（私が認識している限りでは）三つで、parallel_forと、reduction するデータがスカラ型（単一の値のみを持つデータ型）でないときのparallel_reduceと、実行スペースを明示したときのdeep_copyです。これらの関数を用いた際には、必ず適切に同期を取りましょう。

排他制御

前章で触れた、アトミック操作 を行う関数がいくつか用意されています。公式ドキュメントにアトミック関数の一覧があります。

#include <iostream>
#include <Kokkos_Core.hpp>

using namespace Kokkos;

int main() {
initialize();
{
    const int N = 1000;

    // 結果を格納する0次元のViewを用意
    View<int> sum("sum");

    parallel_for("AtomicAdd", N, KOKKOS_LAMBDA(int i) {
        atomic_add(&sum(), i); // sum += i;
    });

    int h_sum;
    deep_copy(h_sum, sum);
    std::cout << h_sum << std::endl;

}
finalize();
}

アトミック操作はスレッド数が多いほど性能が良いですが、スレッド数が少ない場合は データレプリケーション の方が適している場合があります。この切り替えを自動的に行ってくれる、Kokkos::ScatterViewというデータ構造もあり、便利です。

#include <iostream>
#include <Kokkos_Core.hpp>
#include <Kokkos_ScatterView.hpp>

using namespace Kokkos;

int main() {
initialize();
{
    
    const int N = 1000;
    View<int> sum("sum");
    Experimental::ScatterView<int> scatter(sum);
    parallel_for(N, KOKKOS_LAMBDA(int i) {
        auto access = scatter.access();
        access() += i;
    });
    Experimental::contribute(sum, scatter);
    
    View<int> h_sum("host_sum");
    deep_copy(h_sum, sum);
    std::cout << h_sum() << std::endl;

}
finalize();
}

使用例1. ルーレットのサンプリング

次の問題を考えましょう。

ルーレットがあり、選ばれうる項目が$N$個あります。それぞれの項目が選ばれる確率は$P_i(0 \le i \lt N)$です。このルーレットを$M$回だけ回して、それぞれが何回選ばれるかサンプリングしてください。

簡単なアルゴリズムとして、「確率分布の累積和を計算してから、乱数を$[0,1)$の範囲で一様分布に生成して、選ばれた項目を二分探索で探す」を$M$回繰り返すような並列化を考えます。
確率分布の累積和を取る操作はparallel_scanによって並列にできます。$M$回のサンプリング処理に依存関係はありませんから、バカパラできますね。

実装における小さなテクニックとして、std::vectorからデバイスのViewへのコピーは、MemoryTraits<Unmanaged>というプロパティを与えたViewでラップしてからコピーすると無駄がありません。

スレッドごとにランダムな状態を生成したいときは、Random_XorShift64_Poolというクラスを使います。

#include <iostream>
#include <random>
#include <Kokkos_Core.hpp>
#include <Kokkos_ScatterView.hpp>
#include <Kokkos_Random.hpp>

std::vector<double> generateRandomVector(int N) {
    std::vector<double> p(N);
    std::mt19937 gen((unsigned int)std::random_device()());
    std::uniform_real_distribution<> dis(0, 1);

    double p_sum = 0;
    for (size_t i = 0; i < N; ++i) {
        p[i] = dis(gen);
        p_sum += p[i];
    }
    for (size_t i = 0; i < N; ++i) {
        p[i] /= p_sum;
    }
    return p;
}

Kokkos::View<double*> buildPrefixSumsOfDistribution(const std::vector<double>& p_vector) {
    const int N = p_vector.size();
    Kokkos::View<const double*,
                 Kokkos::HostSpace,
                 Kokkos::MemoryTraits<Kokkos::Unmanaged>> h_p(p_vector.data(), N);
    Kokkos::View<double*> p(Kokkos::ViewAllocateWithoutInitializing("distribution"), N);
    Kokkos::deep_copy(p, h_p);
    
    Kokkos::View<double*> prefix_sums("distribution", N + 1);
    Kokkos::parallel_scan(
        N,
        KOKKOS_LAMBDA(int i, double& upd, const bool final) {
            upd += p(i);
            if (final) {
                prefix_sums(i + 1) = upd;
            }
        });
    return prefix_sums;
}

Kokkos::View<int*, Kokkos::HostSpace> getSamplingResult(
            Kokkos::View<double*> prefix_sums_of_distribution, int sampling_count) {
    const int N = prefix_sums_of_distribution.size() - 1;
    Kokkos::View<int*> result("result", N);
    Kokkos::Experimental::ScatterView<int*> scatter(result);
    Kokkos::Random_XorShift64_Pool<> rand_pool((unsigned int)std::random_device()());
    Kokkos::parallel_for(
        sampling_count,
        KOKKOS_LAMBDA(int i) {
            auto rand_gen = rand_pool.get_state();
            double r = rand_gen.drand(0., 1.);
            int lo = 0, hi = prefix_sums_of_distribution.size();
            while (hi - lo > 1) {
                int mid = (lo + hi) / 2;
                if (prefix_sums_of_distribution[mid] > r) {
                    hi = mid;
                } else {
                    lo = mid;
                }
            }
            auto access = scatter.access();
            access(lo)++;
            rand_pool.free_state(rand_gen);
        });
    Kokkos::fence();
    Kokkos::Experimental::contribute(result, scatter);
    return Kokkos::create_mirror_view_and_copy(Kokkos::HostSpace(), result);
}

int main() {
setenv("OMP_PROC_BIND", "spread", 1);
setenv("OMP_PLACES", "threads", 1);
Kokkos::initialize();
{
    
    const int N = 1e5, M = 1e7;
    auto p_vector = generateRandomVector(N);

    Kokkos::Timer tm;
    tm.reset();

    auto prefix_sums_of_distribution = buildPrefixSumsOfDistribution(p_vector);
    auto h_result = getSamplingResult(prefix_sums_of_distribution, M);

    std::cout << "Duration: " << tm.seconds() << std::endl;

    assert(std::accumulate(h_result.data(), h_result.data() + N, 0) == M);

}
Kokkos::finalize();
}

結果は以下の通りです。CPU環境では、逐次実行に比べて約10倍、GPU環境ではなんと約100倍程度の高速化が見られました。

Serial Duration : 1.2083
OpenMP Duration : 0.133902
CUDA Duration   : 0.0133825

使用例2. マンデルブロ集合

マンデルブロ集合をbmp形式の画像で出力するプログラムです。

saveBMP関数はbmpファイルのヘッダやデータ書き込み処理を行う関数であり、非本質なので、説明は省きます。

generateMandelbrot関数では各座標で50回の反復計算を行い、値のノルムが4を超えるまでのループ回数によって色を付けています。この部分は他のピクセルに依存しない独立な処理なので、シンプルなバカパラで処理できます。std::complexは使用できないので、代わりにKokkos::complexというクラスを使って計算します。

最終的にホストにコピーしたいので、デバイスのViewはLayoutRightで計算します。

#include <iostream>
#include <fstream>
#include <cstdlib>
#include <Kokkos_Core.hpp>
#include <Kokkos_Timer.hpp>

const int MAX_ITER = 50;

struct RGB {
    unsigned char r, g, b;
};

void saveBMP(const char* filename, Kokkos::View<RGB**, Kokkos::HostSpace> h_pixels) {
    const int HEIGHT = h_pixels.extent(0), WIDTH = h_pixels.extent(1);
    int filesize = 54 + 3 * WIDTH * HEIGHT;
    unsigned char bmpfileheader[14] = {'B', 'M', 0, 0, 0, 0, 0, 0, 0, 0, 54, 0, 0, 0};
    unsigned char bmpinfoheader[40] = {40, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 0, 24, 0};

    bmpfileheader[ 2] = (unsigned char)(filesize    );
    bmpfileheader[ 3] = (unsigned char)(filesize>> 8);
    bmpfileheader[ 4] = (unsigned char)(filesize>>16);
    bmpfileheader[ 5] = (unsigned char)(filesize>>24);

    bmpinfoheader[ 4] = (unsigned char)(WIDTH    );
    bmpinfoheader[ 5] = (unsigned char)(WIDTH>> 8);
    bmpinfoheader[ 6] = (unsigned char)(WIDTH>>16);
    bmpinfoheader[ 7] = (unsigned char)(WIDTH>>24);
    bmpinfoheader[ 8] = (unsigned char)(HEIGHT    );
    bmpinfoheader[ 9] = (unsigned char)(HEIGHT>> 8);
    bmpinfoheader[10] = (unsigned char)(HEIGHT>>16);
    bmpinfoheader[11] = (unsigned char)(HEIGHT>>24);

    std::ofstream out(filename, std::ios::out | std::ios::binary);
    out.write(reinterpret_cast<char*>(bmpfileheader), 14);
    out.write(reinterpret_cast<char*>(bmpinfoheader), 40);

    for (int y = 0; y < HEIGHT; y++) {
        for (int x = 0; x < WIDTH; x++) {
            RGB& pixel = h_pixels(HEIGHT - y - 1, x);
            unsigned char color[3] = {pixel.b, pixel.g, pixel.r};
            out.write(reinterpret_cast<char*>(color), 3);
        }
    }
    out.close();
}

Kokkos::View<RGB**, Kokkos::HostSpace> generateMandelbrot(const int HEIGHT, const int WIDTH) {
    Kokkos::View<RGB**, Kokkos::LayoutRight> pixels("pixels", HEIGHT, WIDTH);
    Kokkos::parallel_for(Kokkos::MDRangePolicy<Kokkos::Rank<2>>({0, 0}, {HEIGHT, WIDTH}), KOKKOS_LAMBDA(int y, int x) {
        Kokkos::complex<double> point((x - WIDTH/2.0) * 4.0 / WIDTH, (y - HEIGHT/2.0) * 4.0 / HEIGHT);
        Kokkos::complex<double> z(0, 0);
        int iter = 0;
        while (z.real() * z.real() + z.imag() + z.imag() < 4.0 && iter < MAX_ITER) {
            z = z*z + point;
            iter++;
        }
        if (iter < MAX_ITER) {
            pixels(y, x).r = iter;
            pixels(y, x).g = iter * 2;
            pixels(y, x).b = iter * 5;
        }
    });
    return Kokkos::create_mirror_view_and_copy(Kokkos::HostSpace(), pixels);
}

int main() {
setenv("OMP_PROC_BIND", "spread", 1);
setenv("OMP_PLACES", "threads", 1);
Kokkos::initialize();
{
    Kokkos::Timer tm;
    tm.reset();

    const int HEIGHT = 6400, WIDTH = 6400;
    auto h_pixels = generateMandelbrot(HEIGHT, WIDTH);

    std::cout << "Duration: " << tm.seconds() << "\n";

    saveBMP("mandelbrot.bmp", h_pixels);
    std::cout << "Mandelbrot image saved as mandelbrot.bmp" << std::endl;

}
Kokkos::finalize();
}

各ピクセルの色を計算し、ホストにデータを渡すまでの時間は、環境ごとに以下のような結果になりました。CPU/GPU環境ではあまり差は見られませんが、逐次実行に比べておよそ6から7倍程度高速化していますね。

Serial Duration : 0.687302 
OpenMP Duration : 0.0968205
CUDA Duration   : 0.0906864

付録

performance capability という数値がGPUごとに決められていて、Kokkosのビルドオプションを、これに合うように設定する必要があります。リポジトリのscripts/build.shには-DKokkos_ARCH_AMPERE86=ON \という行が書いていますが、これを各アーキテクチャのキーワードに変更してください。

GPUの performance capability を確認するには、CUDAの開発者向けサイトを、Kokkosにおけるキーワードを確認するには、Kokkos公式ドキュメントを参照してください。

参考