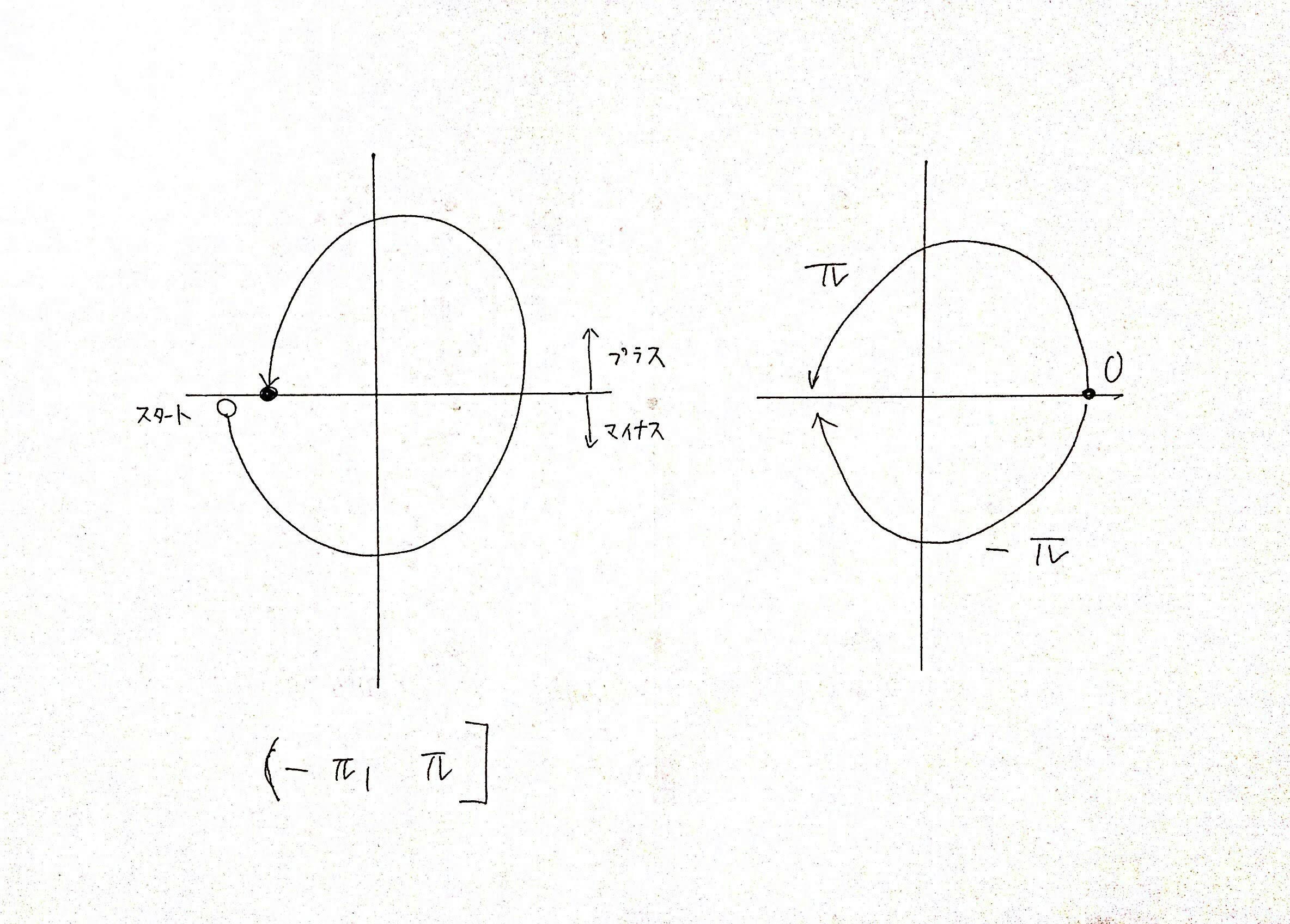はじめに
競技プログラミングの問題では、たまに平面幾何という分野の問題が出てきます。
これは、ベクトルや三角形、凸多角形などの平面的な図形に関する問題です。
AtCoderではあまりでませんが、ICPCでは非常に頻出するジャンルです。
この平面幾何の問題では、$N$個の二次元座標上の点が与えられることが多くありますが、これらを反時計回りにソートしたいことがあります。
つまり、$N$個の点が与えられますが順番がバラバラなので
反時計回りになるように配列内の順番をソートしたい、ということです。
偏角ソートを行う問題は、前回のABC139-Fで出てきました。
残念ながら偏角ソートをやる方法を知らなかったので、今回は雑な方法を見ていこうと思います。
偏角
偏角とは
そもそも偏角とはなんでしょうか?
僕は分かりません。
具体例で学ぶ数学 - 複素数の偏角の求め方と公式で学んでみます。
偏角とは、複素平面上で、正の実軸$x$軸から点$z$までの反時計周りの角度と定義されます。
複素平面では$arg(z)$という表記で、$z$の偏角を表すことが多いです。
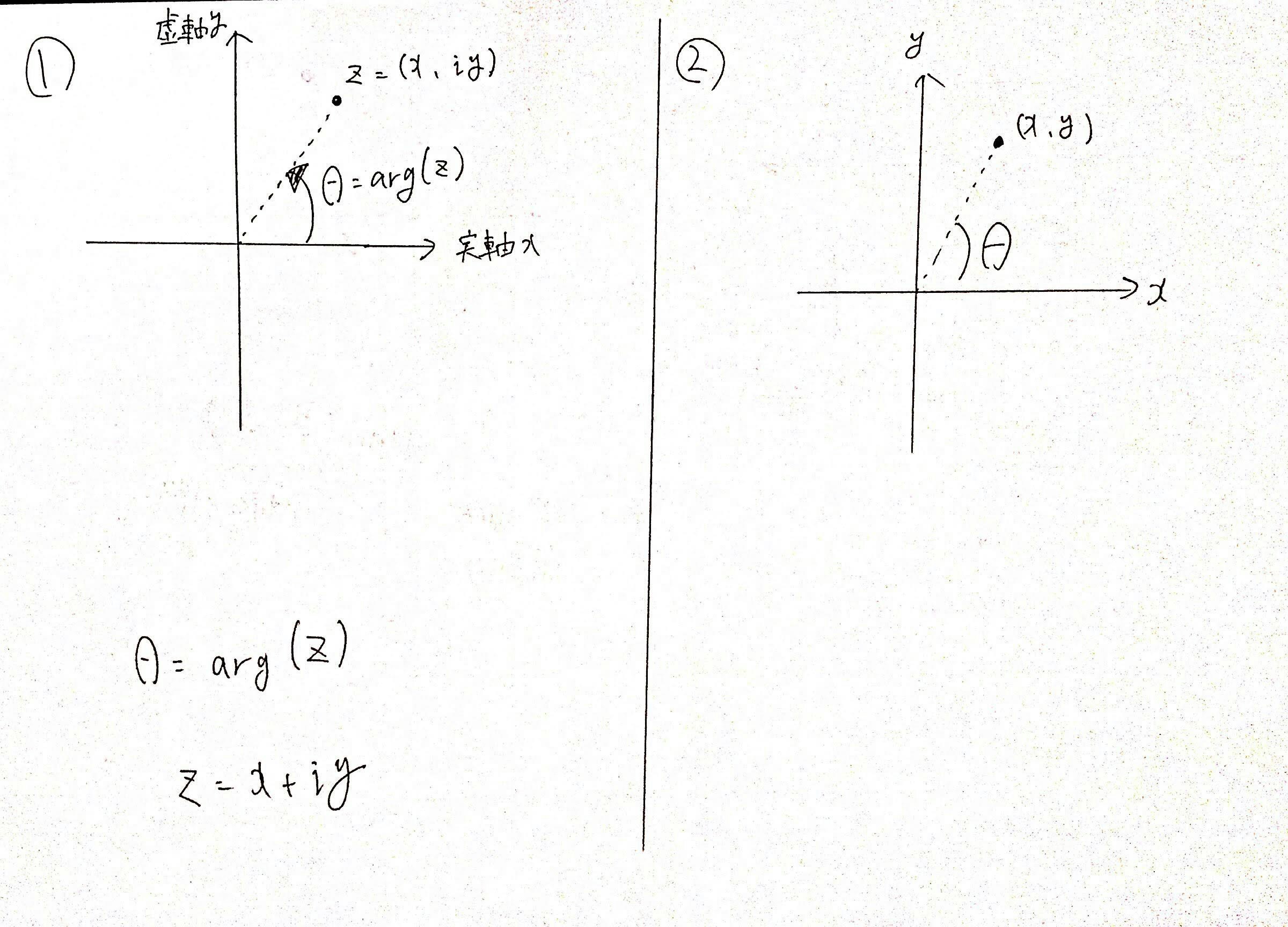
以下の①のような状態です。
ただし、同じ考えは通常の二次元座標でも考えることができて
$x$軸からの点$z$までの反時計周りの角度と見ることもできます。
②のような状態です。
偏角の求め方
偏角が複素平面上の点$z$への$x$軸からの角度、ということがわかりました。
それでは、この偏角が何ラジアンなのかはどう求めればよいのでしょうか?
現在、分かっていることはこの点$z$は
複素平面上では、$z=(x, iy)$
二次元平面上では、$z=(x, y)$の状態です。
ここで、三角関数と逆三角関数を考えてみます。
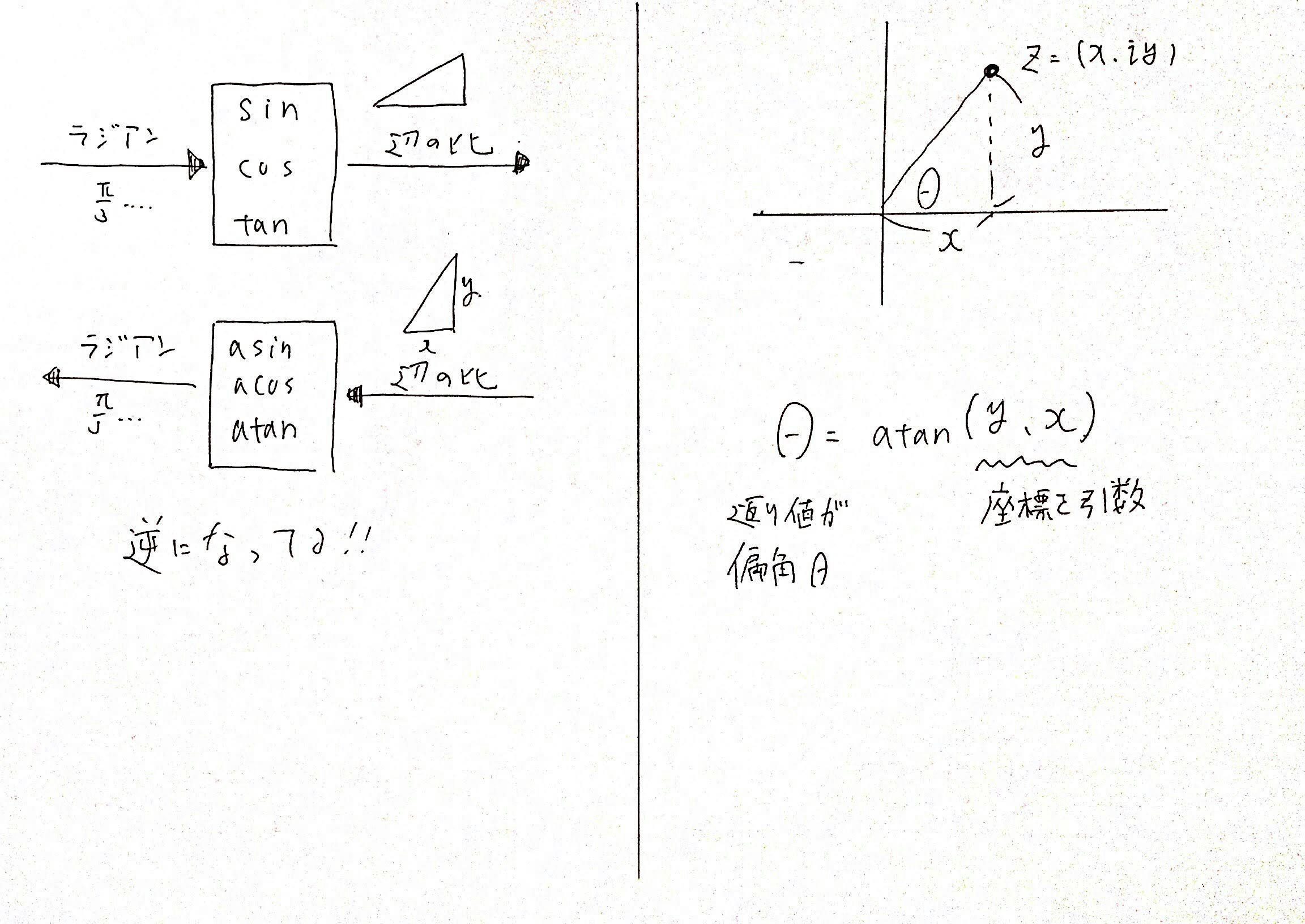
三角関数はラジアンを受け取って、三角形の辺の比を返します。
逆三角関数は三角形の辺の比を受け取って、ラジアンを返します。
現在、$z = (x, y)$という座標が分かっているため
原点と点$z$からなる三角形の辺の比は分かります。
よって、逆三角関数の$tan^{-1}(or \ atan)$関数を使えば偏角が求められます。
多くのプログラミング言語では、$atan$として、tanの逆関数が定義されています。
C++のatan, atan2関数
このようにプログラミングでは、tanの逆関数である
$atan$に点の座標や辺の比を与えるだけで、偏角$arg(z)$を求められるようになっています。
しかし、C++(C言語)では、tanの逆関数に関して似たような関数があり、大きく分けるとatan, atan2の2つがあります。
それぞれを見てみましょう。
atan
C++の$atan$関数は、辺の比を引数にして、偏角をラジアンで返します。
この辺の比というのが重要で、例えば$z = (x, y)$という点$z$があったとします。
このとき、C++では偏角を以下のように計算します。
int main() {
double x, y;
cin >> x >> y;
//偏角argz
cout << atan(y / x) << endl;
}
辺の比を引数にとるため、$y / x$をユーザが計算して渡さなければいけません。
atan2
C++の$atan2$関数は、座標$(x, y)$を引数にして、偏角をラジアンで返します。
座標を受け取る、というのが$atan$と異なる点です。
以下のように偏角を計算します。
int main() {
double x, y;
cin >> x >> y;
//偏角argz
cout << atan2(y, x) << endl;
}
一個目の引数で$y$、二個目の引数で$x$を取ることに注意してください。
これは、わり算のそのままの順番のように見えるように設計されているためだと思います。
atanとatan2は挙動が違う
tyu_ru_cppさんからコメントをいただきました!
自分は、$atan$と$atan2$が同じだと勘違いしていましたが、それぞれ異なる概念・挙動を行うようです。
ご指摘ありがとうございます。
$atan$, $atan2$の意味の違いは
具体例で学ぶ数学で丁寧に解説されています。
こちらを参考にするとわかりやすいです。
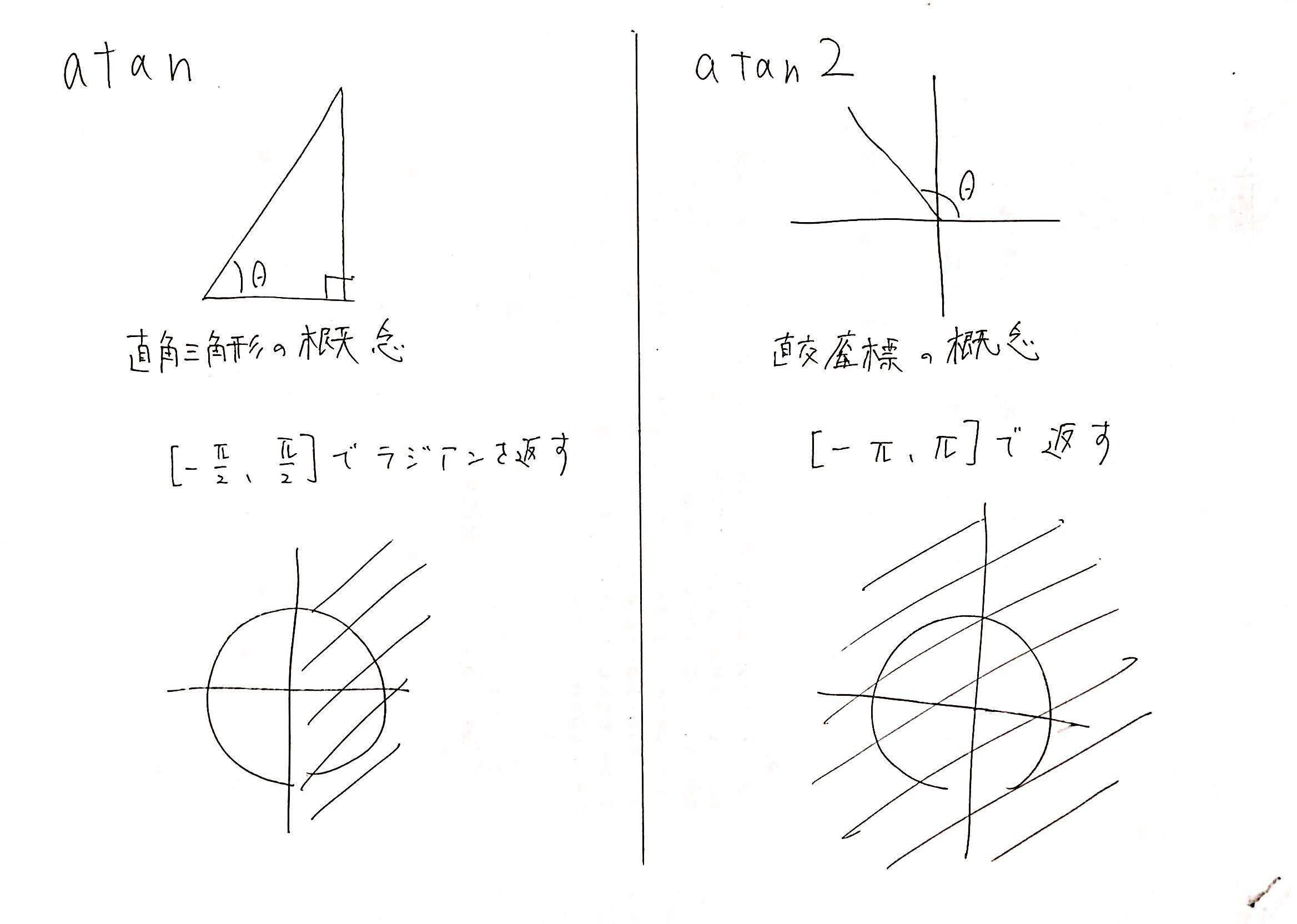
$atan$は三角比を元に、$[-{\pi}/2, {\pi}/2]$の範囲のラジアンを返します。
$atan2$は直交座標の$(x, y)$を元に、$[-{\pi}, {\pi}]$の範囲のラジアンを返します。
よって、偏角ソートではxy直交座標の1-4象限すべてのラジアンが欲しいため、$atan2$を使う必要があります。
atan2の振る舞いを見てみる
$atan2$と$atan$では、$atan2$がより抽象的で大きい概念であり、偏角ソートには$atan2$が必要です。
よって、これ以降は$atan2$で考えていきます。
$atan2$が、$(x,y)$座標を受け取って、その座標と$x$軸のなす角ということは分かりましたが、どう実際に動くのでしょうか。
動きを理解するために以下のようなプログラムを動かしてみます。
int main() {
cout << atan2(0, 0) << endl; // 1
cout << atan2(0, 1) << endl; // 2
cout << atan2(1, 1) << endl; // 3
cout << atan2(1, 0) << endl; // 4
cout << atan2(1, -1) << endl; // 5
cout << atan2(0, -1) << endl; // 6
cout << atan2(-1, -1) << endl; // 7
cout << atan2(-1, 0) << endl; // 8
cout << atan2(-1, 1) << endl; // 9
}
これは以下のような実行結果になります。
0
0
0.785398
1.5708
2.35619
3.14159
-2.35619
-1.5708
-0.785398
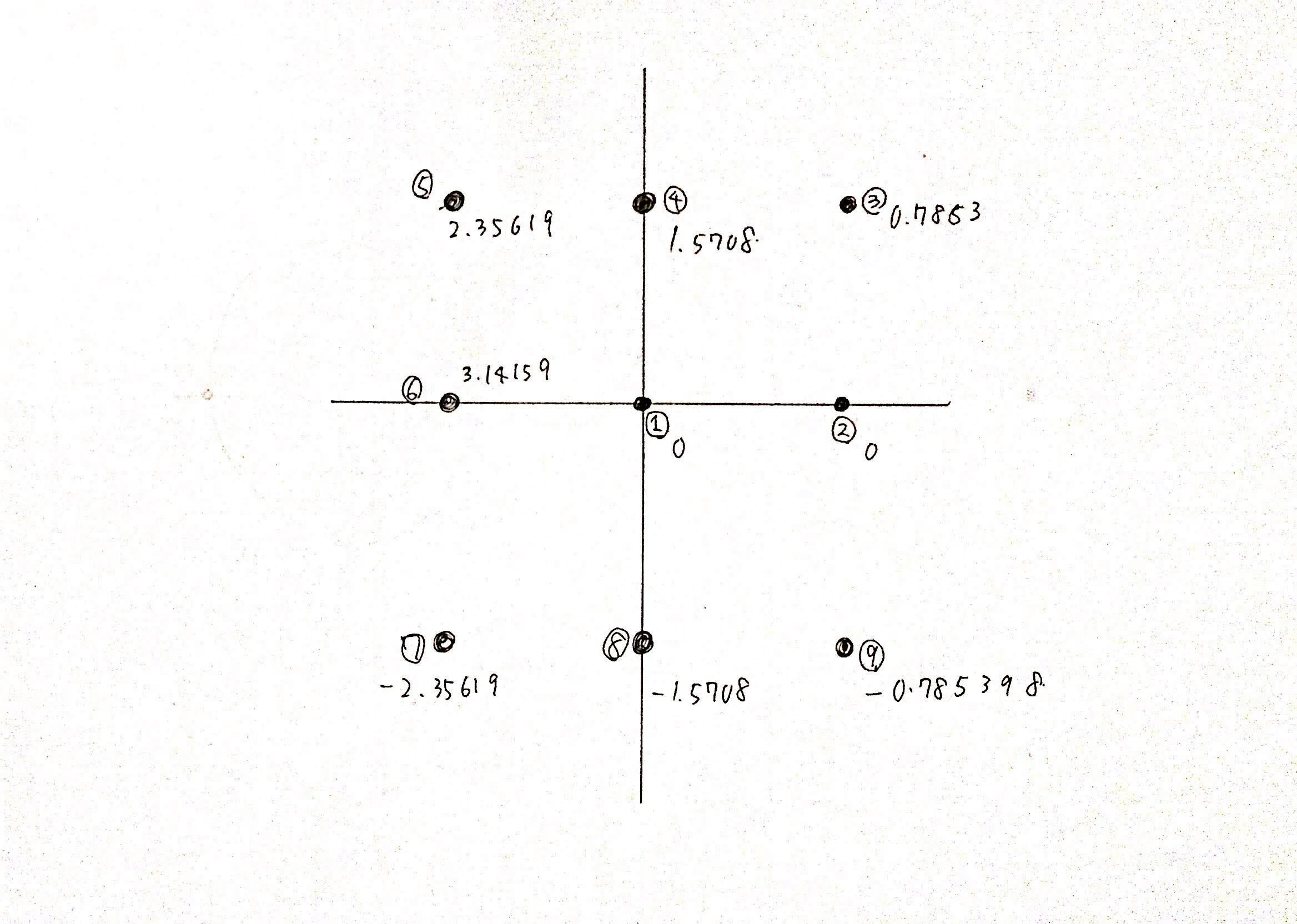
また、以下のような座標配置になります。
よって、偏角を求めてソートを行えば
第3 -> 第4 -> 第1 -> 第2象限のような順番で並び
反時計回りにソートすることができます。
注意点としては偏角の返り値の範囲が
$[-{\pi}, {\pi}]$のように、$x$軸の負側の軸上は一番大きい${\pi}$そのものに扱われることに注意しましょう。
偏角ソート・反時計ソート
長くなりましたが、それでは実際に偏角ソート、反時計ソートをします。
ここで、平面幾何では、浮動小数点が絡んでくるためlong double型で実装することにします。
typedef long double LD;
int main() {
//ランダムに生成する点の数
int N;
cin >> N;
mt19937 mt;
uniform_int_distribution<int> dist(-100, 100);
vector<LD> x(N), y(N);
for (int i = 0; i < N; i++) {
x[i] = dist(mt);
y[i] = dist(mt);
}
}
まず、ランダムに生成する点の数$N$をコンソールから入力します。
そして、その後は、実際にランダム生成で$x, y$座標を$N$点分作ります。
しかし、このままではソートする時に、ソート対象が分離していると面倒なのでpairでまとめるようにします。
typedef long double LD;
int main() {
//ランダムに生成する点の数
int N;
cin >> N;
mt19937 mt;
uniform_int_distribution<int> dist(-100, 100);
vector<LD> x(N), y(N);
for (int i = 0; i < N; i++) {
x[i] = dist(mt);
y[i] = dist(mt);
}
vector<pair<LD, LD>> xy(N);
for (int i = 0; i < N; i++) xy[i] = make_pair(x[i], y[i]);
}
これで、$xy$として、座標$(x, y)$を一個の変数として扱うことができました。
あとは偏角、反時計回りにソートするだけです。
以下のように、ラムダ式で書いてみましょう。
typedef long double LD;
int main() {
//ランダムに生成する点の数
int N;
cin >> N;
mt19937 mt;
uniform_int_distribution<int> dist(-100, 100);
vector<LD> x(N), y(N);
for (int i = 0; i < N; i++) {
x[i] = dist(mt);
y[i] = dist(mt);
}
vector<pair<LD, LD>> xy(N);
for (int i = 0; i < N; i++) xy[i] = make_pair(x[i], y[i]);
sort(xy.begin(), xy.end(), [](const auto &p1, const auto &p2) {
return atan2l(p1.second, p1.first) < atan2l(p2.second, p2.first);
});
}
atan2lは、long double用のtanの逆関数ライブラリです。
これによって、より偏角が小さい順にクイックソートすることができます。
それでは結果を確かめるためにソートされたか出力してみましょう。
typedef long double LD;
int main() {
//ランダムに生成する点の数
int N;
cin >> N;
mt19937 mt;
uniform_int_distribution<int> dist(-100, 100);
vector<LD> x(N), y(N);
for (int i = 0; i < N; i++) {
x[i] = dist(mt);
y[i] = dist(mt);
}
vector<pair<LD, LD>> xy(N);
for (int i = 0; i < N; i++) xy[i] = make_pair(x[i], y[i]);
sort(xy.begin(), xy.end(), [](const auto &p1, const auto &p2) {
return atan2l(p1.second, p1.first) < atan2l(p2.second, p2.first);
});
for (int i = 0; i < N; i++) {
cout << "(" << xy[i].first << ", " << xy[i].second << ") : " << atan2l(xy[i].second, xy[i].first) << endl;
}
}
例えば、$N=20$とすると以下のようになります。
20
(-11, -8) : -2.5128
(-56, -95) : -2.10344
(-18, -76) : -1.80335
(-5, -84) : -1.63025
(-1, -63) : -1.58667
(9, -62) : -1.42664
(74, -93) : -0.898683
(96, -74) : -0.656702
(86, -57) : -0.585314
(97, -24) : -0.242551
(71, 36) : 0.469266
(43, 28) : 0.577192
(5, 73) : 1.50241
(-11, 61) : 1.74921
(-24, 86) : 1.84294
(-8, 21) : 1.93478
(-45, 70) : 2.14213
(-41, 41) : 2.35619
(-83, 79) : 2.38088
(-51, 22) : 2.73434
座標にプロットしてみると分かりますがきちんと反時計回りになっています。
まとめ
C++で、最も簡単に偏角ソートをしたい場合は
tanの逆関数であるatan2関数で、$x$軸から点$z$までの偏角を求めればよいです。
そして、その偏角を用いてソートすることで、反時計回りに点たちを並べることができます。
ただし、注意点として$3, 4, 1, 2$という象限で並ぶことに注意する必要があります。
($[-{\pi}, {\pi}]$というラジアンの範囲で返すためです。)
しかし
しかしながら、この偏角ソートには問題があります。
それは浮動小数点の精度誤差という問題です。
long double型は環境によりますが64ビットだったり128ビットだったりの表現のされ方をします。
しかし、これはまったくもって正確でなく、ものすごく小さい値やものすごく大きい値になると、比較に失敗することが多いです。
また、同じ値を作って等価である、と判定したい場合でも、小さい誤差が生まれて異なる数値であると判定されたりします。
次回は、精度のよい偏角ソートの実装を目的とします。