はじめに
今回は機械学習アルゴリズムの決定木(Decision Tree)についてまとめました。決定木の発展系であるランダムフォレストやXGBoostなどを理解していくために、しっかりと基礎を理解していきたいと思います。
参考
決定木の理解に当たって下記を参考にさせていただきました。
決定木(Decission Tree)
決定木の概要
決定木は条件による分岐を「根」からたどることで、最も条件に合致する「葉」を検索するアルゴリズムです。学習データをもとに説明変数から成る条件式をノードとして作成し、「葉」の部分で予測結果を導き出せるようなモデルを自動作成します。分類問題、回帰問題、どちらにも対応が可能でそれらは各々回帰木・分類木と呼ばれています。
メリットとデメリットは下記のようなものがありますが、解釈が容易というメリットが最も決定木を使用する理由になるかなと思います。
メリット
- 解釈が容易(何を特徴量として判断しているのか明確に可視化できる)
- 様々な尺度のデータをそのまま扱える(スケーリング等の前処理が不要)
デメリット
- 決して分類性能が高い手法ではない
- 過学習を起こしやすい
- 線型性のあるデータに適していない
決定木のイメージ
簡単にsklearnのirisデータセットに対して決定木のアルゴリズムを学習させ、決定木を描画してみます。
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
iris = load_iris()
X = iris.data[:,2:]
y = iris.target
tree_clf = DecisionTreeClassifier(max_depth=2, random_state=42)
tree_clf.fit(X, y)
from graphviz import Source
from sklearn.tree import export_graphviz
export_graphviz(
tree_clf,
out_file=os.path.join("iris_tree.dot"),
feature_names=iris.feature_names[2:],
class_names=iris.target_names,
rounded=True,
filled=True
)
下記はコマンドラインで実行(dotファイルをpngに変換するため)
$ dot -Tpng iris_tree.dot -o iris_tree.png
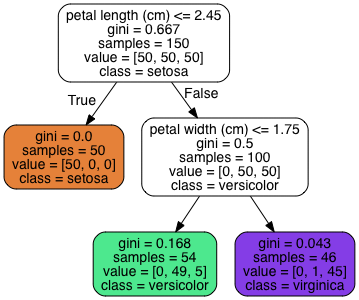
すると下記のような決定木を出力することができます。
条件に合致するか否か(True or False)で分岐していき、色がついているノードが「葉」として最終的な予測結果を導き出します。
決定木の学習と不純度(impurity)
決定木の各ノードが上手く条件分岐を作成できているか否かを見る指標として不純度(impurity)というものがあります。更にその不純度(impurity)を計測する手法としてジニ不純度(GINI inpurity)とエントロピーの二つがあります。
※所得の不平等さを測る指標としてよく使用されるジニ係数とは全く異なるものなので注意
ジニ不純度(GINI inpurity)
$n$をデータに含まれるクラスの個数、$p_{i}$をデータがクラス$i$である確率であるとすると、ジニ不純度は下記の数式で表すことができます。
Gini(p) = \sum_{i=1}^{n} p_{i}(1-p_{i}) = 1-\sum_{i=1}^{n} p_{i}^2
数式だけだとわかりにくいので具体例を見てみましょう。
再度先ほど例示した決定木の緑色のノードの部分を確認します。こちらのvaluesの値がこの条件分岐においてそれぞれのクラスにデータが何件ずつ分類できているかを表しており、classの値がこの条件分岐の時にこの分類と判定する、というものを表しています。
緑のノードのvaluesを確認すると[0, 49, 5]となっており、これはこの条件分岐において0件のデータがセトサに、49件のデータがバーシクルに、5件のデータがバージニカに分類されているという意味です。ただ今回classの値はバーシクルになっているため、本来であれば全てバーシクルに分類されている状態がベストです。つまり、それ以外に分類されているものは不純物と言えるため、決定木ではそれを定量的に測る不純度という指標が学習に用いられます。
今回の具体例のジニ不純度を計算してみます。
1 - (\dfrac{49}{50})^2 - (\dfrac{5}{50})^2 \approx 0.168
ジニ不純度を算出することができました。緑色のノード内のginiの値と一致していることがわかるかと思います。
エントロピー(entropy)
不純度の指標としてエントピーを用いることも可能です。エントロピーは情報理論の考え方をベースとした乱雑さを表す概念です。エントロピーが大きければ乱雑=不純度が高いというイメージです。エントロピーの概念の説明は以前の記事で行なっているのでよろしければそちらもご参照ください。
エントロピーは下記のような数式で表されます。
H(p) = -\sum_{i=1}^{n} p_{i}log_{2}(p_{i})
ジニ不純度の時と同じく緑ノードのエントピーを計算してみます。
-(\dfrac{49}{50})log_{2}(\dfrac{49}{50}) - (\dfrac{5}{50})log_{2}(\dfrac{5}{50}) \approx 0.445
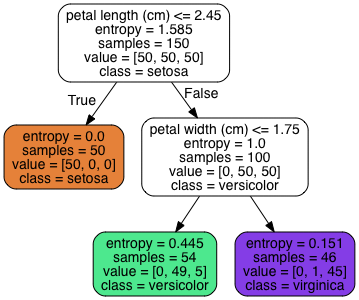
sklearn上でもモデルを学習する際の引数としてcriterion = 'entropy'を与えることで不純度をエントロピー(entropy)として学習を進めることができます。下記決定木ではginiの代わりにentropyが入っていることがわかります。
※sklearnのデフォルトの計算では対数の底は2として計算が行われるため、上記でも対数の底は2で記載しています。対数の底をネイピア数で記載しても問題ありません。
基本的にはジニ不純度を用いてもエントロピーを用いても学習結果に大差はないとされているようですが、ジニ不純度の方を用いた方が僅かに計算スピードが速いらしいです。
CART訓練アルゴリズム
決定木の中にもいくつかのアルゴリズムがありますが、今回は最もベーシックなCART(Classification and Regression Tree)をご紹介します。sklearnのアルゴリズムはCARTを使用しています。CARTは各ノードにおいて2択の条件分岐(Yes or No)しか作成しないアルゴリズムで、下記のようなコスト関数が最小になるように分岐を作成します。
ある一つの特徴量を$k$とし、その$k$を対象として閾値$t_{k}$でデータを2つに分割することを考えます。この時、最適な$k$と$t_{t}$は下記損失関数を最小化することで得ることができます。
L(k, t_{t}) = \dfrac{n_{right}}{n}Gini_{right} + \dfrac{n_{left}}{n}Gini_{left}
- $Gini_{right}/Gini_{right}$はそれぞれ左右分割後の不純度
- $n_{right}/n_{left}$はそれぞれ左右分割後のデータ数
上記数式の意味としては、左右分割後のノードの不純度のデータ数での加重平均を表していて、こちらを最小化することで最適な閾値を探すことができます。
※上記は不純度にジニ不純度の指標を用いる想定で記載。エントロピーを用いても良い。
決定木のパラメーター
決定木はこれ以上分割しても不純度が低下しないラインまで深く分岐を作成し続けます。
ただ決定木は与えた学習データに過剰適合しやすい性質を持っているため、自由な深さまで分岐を作成することを許すと容易に過学習を起こしてしまいます。
その対策として決定木の木の形を制限するようなパラメーターを与えます。代表な的なものとして木の深さを制限するパラメーター(sklearnでは"max_depth")やノードを分割するために必要なサンプル数の下限(sklearnでは"min_sample_leaf")などがあります。
決定木を用いた文書分類
sklearnを用いた決定木モデルの作成
以下ではライブラリを用いて実際に決定木のモデルを作成していきます。
使用したライブラリ
scikit-learn 0.21.3
データセット
sklearnを用いて簡単に決定木のモデルを簡単に作成することが可能です。今回データセットは「livedoor ニュースコーパス」を使用させていただきます。データセットの詳細やその形態素解析の方法は以前投稿した記事で投稿しているの気になる方そちらをご参照いただければと思います。
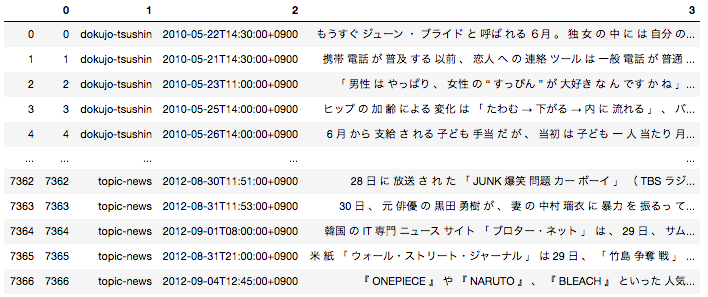
日本語の場合は事前に文章を形態素単位に分解する前処理が必要となるため、全ての文章を形態素に分解した後下記のようなデータフレームに落とし込んでいます。
一番右のカラムが文章を全て形態素解析して半角スペースごとに区切ったものになります。こちらを用いて決定木のモデルを作成します。
モデルの学習
sklearnを用いて決定木のモデルの作成を行います。下記がモデルを作成するに当たっての主要なパラメータになります。
| パラメーター名 | パラメータの意味 |
|---|---|
| criterion | {“gini”, “entropy”}不純度の指標としてジニ不純度を用いるか、エントロピーを用いるか |
| max_depth | 決定木の深さをどこまで許すかの最大値(設定しない場合、非常に複雑な決定木を作成してしうまう可能性があり汎化性能に関わる) |
| min_samples_split | ノードを分割するに当たっての必要なサンプル数の最小値(最小値が小さいと細かい分割をするモデルが作成されてしまう可能性があり、汎化性能に関わる) |
| min_samples_leaf | 葉の中に最低でも残しておく必要のあるサンプル数の最小値(上記と同様に最小値が小さいと細かい分割をするモデルが作成されてしまう可能性があり、汎化性能に関わる) |
今回は文章をBag-of-words形式(各文章にそれぞれの単語が何単語入っているかをカウントしてベクトル化したもの)に変換した後そのベクトルを決定木にかけます。'it-life-hack'というit系の記事と'sports-watch'というスポーツ系の記事の分類を試みます。
import pandas as pd
import pickle
# 形態素分解した後のデータフレームはすでにpickle化して持っている状態を想定
with open('df_wakati.pickle', 'rb') as f:
df = pickle.load(f)
# 今回に2つの種類の記事を分類できるかを検証
ddf = df[(df[1]=='sports-watch') | (df[1]=='it-life-hack')].reset_index(drop = True)
# sklearnのライブラリを用いて文章をbag-of-words形式に変換
from sklearn.feature_extraction.text import CountVectorizer
vectorizer = CountVectorizer(token_pattern="(?u)\\b\\w+\\b")
X = vectorizer.fit_transform(ddf[3])
# 記事の種別を数値に変換
def convert(x):
if x == 'it-life-hack':
return 0
elif x == 'sports-watch':
return 1
from sklearn.datasets import load_iris
from sklearn.tree import DecisionTreeClassifier
from sklearn.model_selection import train_test_split
iris = load_iris()
X = X
y = ddf[1].apply(lambda x : convert(x))
# 訓練データと評価データを分割する
X_train, X_test, y_train, y_test = train_test_split(X, y, train_size=0.7, random_state=42)
# モデルを学習
tree_clf = DecisionTreeClassifier(criterion = 'gini', max_depth=4, min_samples_leaf = 10,random_state=42)
tree_clf.fit(X_train, y_train)
# 評価データに対する結果を出力
print(tree_clf.score(X_test, y_test))
精度として出力された値はこちらになります。想像以上に精度が良いですね。
it関連の記事とスポーツ関連の記事ではやはり使用されている単語に明確な差異があるようです。
0.9529190207156308
それでは今回作成したモデルを可視化してみます。
from graphviz import Source
from sklearn.tree import export_graphviz
import os
export_graphviz(
tree_clf,
out_file=os.path.join("text_classification.dot"),
feature_names=vectorizer.get_feature_names(),
class_names=['it-life-hack', 'sports-watch'],
rounded=True,
filled=True
)
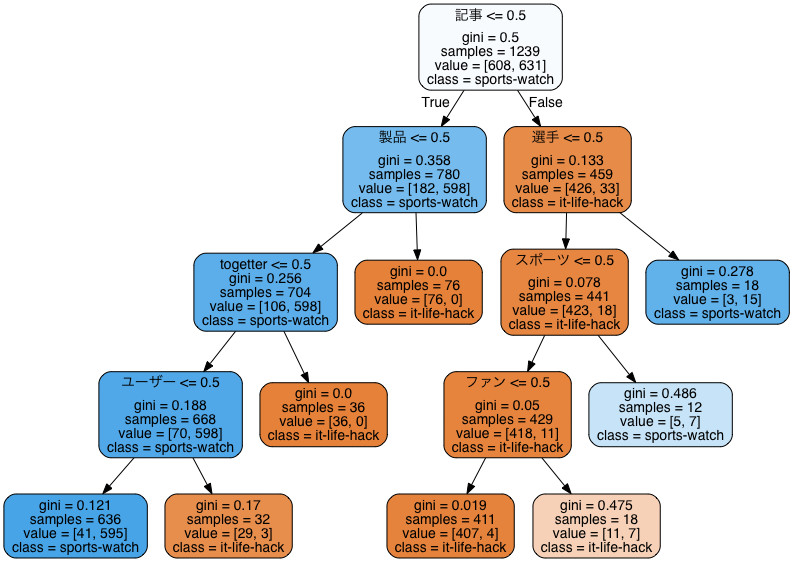
下記はコマンドとして実行
$ dot -Tpng text_classification.dot -o text_classification.png
「製品」や「選手」など、何となく納得感のある特徴量をノードを分割する条件として採用していることがわかります。中身がブラックボックスではないことがやはり大きな強みですね。
Next
決定木の発展系であるランダムフォレストやAdaboost、Xgboost、lightGBM等も順を追って勉強していきたいと思います。