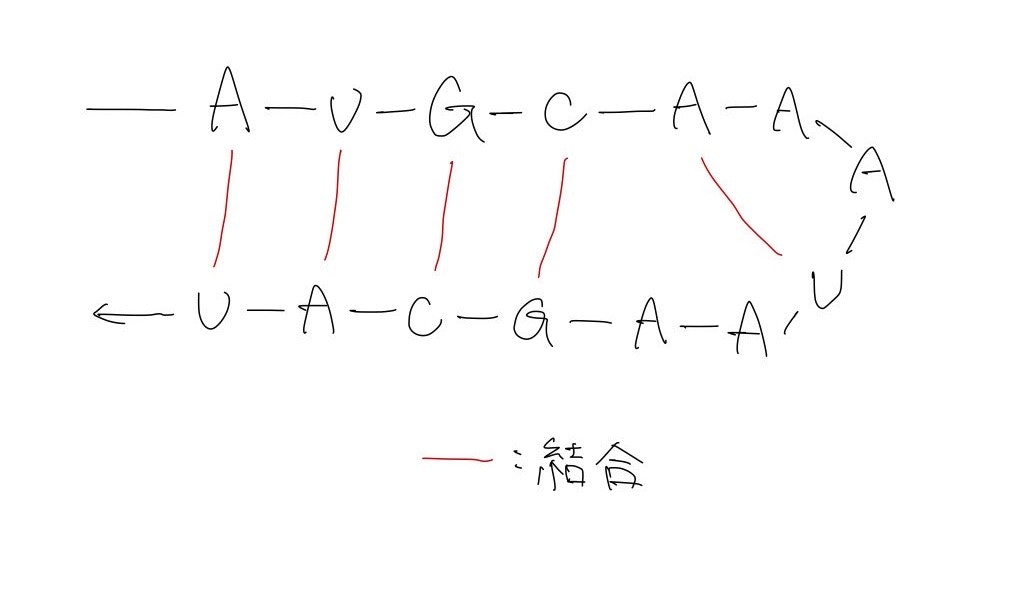Nussinovアルゴリズムを実装する

はじめに

この記事では、まず、RNA二次構造予測のための動的計画法である Nussinov アルゴリズムについて説明します。その次に、Nussinov アルゴリズムをGo言語で実装します。

雑談
先日（令和7年度秋期）の応用情報技術者試験にて、「二つの列の最長共通部分列の長さを求めるアルゴリズム」の問題が出ました。最長共通部分列の長さは、2本の塩基配列の類似度を測る目的などに用いられます。
ちょうど私自身、学生時代にバイオインフォマティクスを専攻していたこともあり、このテーマに親近感を覚えたので、今回のNussinovアルゴリズムの記事を書きました。

Nussinovアルゴリズムとは

Nussinov（ヌシノフ）アルゴリズムは、動的計画法を用いてRNAの二次構造を予測する古典的なアルゴリズムのことです。1970年代後半に、生物学者の Ruth Nussinov によって提案されました。

前提知識
RNAは、４種類の塩基 A（アデニン）, U（ウラシル）, G（グアニン）, C（シトシン）から構成されており、A は U と、G は C との間でのみ水素結合を形成します。
塩基が鎖状に連なったものを塩基配列と呼び、結合によって形成される構造を二次構造といいます。塩基配列の構造は、配列中の塩基が結合を作る箇所によって異なります。

ある塩基配列がとりうる構造の数は、配列の長さに対して膨大に増加します。
Nussinovアルゴリズムでは、その膨大な数のとりうる構造の中で、「配列中のどの塩基同士が結合を作るか」を計算し、最大数のペアを作る構造を求めます。

ただし今回は、簡単のために、ペアの最大数を求めることとします。また、線形な二次構造のみを扱うこととします。

たとえば、UCGACCAAAAGGGCGA という配列が与えられたとき、この塩基配列はさまざまな構造をとる可能性があります。具体的には、((..(.....).)..),.(...(....).)..., (((.((....)).))) などの構造をとります（構造をドットブラケット記法で示しています）。
配列 UCGACCAAAAGGGCGA がとりうる無数の構造のうち、最大数のペアを作る構造は (((.((....)).))) です。このときのペア数は 5 です。Nussinovアルゴリズムでは、これを求めます。

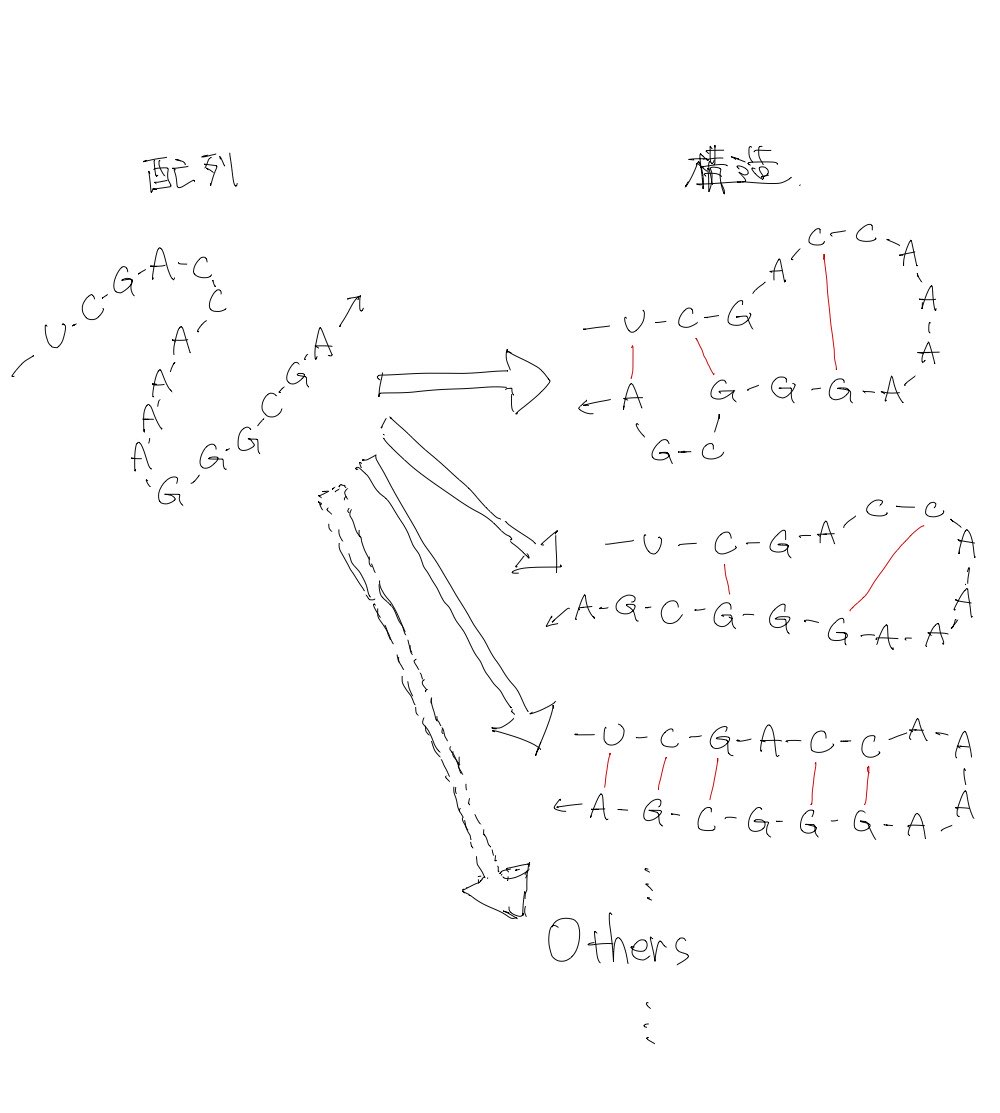
つまりNussinovアルゴリズムでは、ある塩基配列が与えられたとき、その配列がとりうる構造のうち、最大のペア数を作る構造のペア数を計算します。

なお、配列の長さが3以下である場合は、その長さは0となります。

定式化

定義

部分配列がとりうる構造の最大のペア数

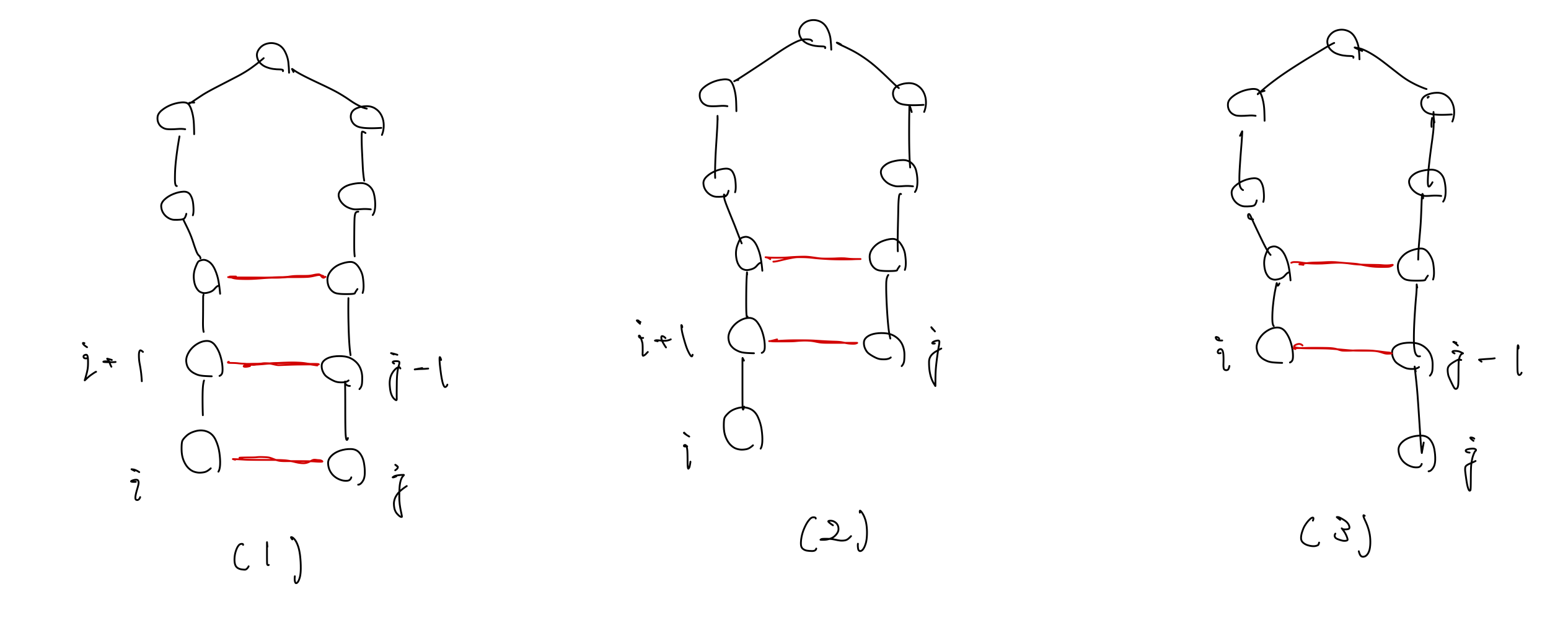
長さ$n$の塩基配列の$i$番目から$j$番目までの部分配列がとりうる構造において、最大のペア数を$M(i,j)$とする$(1\leq i\leq j\leq n)$。$M(i,j)$を計算するために、以下の3つに場合分けを行う。

(1) 塩基 i と j が結合を形成するとき

塩基$i$と塩基$j$が、AとU、またはGとCであった場合、塩基$i$と塩基$j$は結合を形成する。このとき$M(i,j)$は、$M(i+1,j-1)$の結合数に、塩基$i$と$j$の結合分を足すことで計算できる。つまり、$M(i+1,j-1)+1$によって計算できる。

(2) 塩基 i が結合を形成しないとき

このとき配列から塩基$i$を取り除いても、最大のペア数$M$には影響しないので、$M(i,j)$は、$M(i+1,j)$に等しい。

(3) 塩基 j が結合を形成しないとき

このとき$M(i,j)$は、$M(i,j-1)$に等しい。

塩基が結合を表すスコア関数

配列中の$i$番目の塩基と$j$番目の塩基が結合を形成するかどうかを、パラメータ$Score(i,j)$で表す。

Score(i,j) = \left\{
\begin{array}{ll}
1 \quad (塩基 i と塩基 j が結合を形成するとき) \\
0 \quad \text{otherwise}
\end{array}
\right.

たとえば、塩基$i$が A(アデニン) のとき、塩基$j$が U(ウラシル) であれば、結合を形成するため、$Score(i,j) = 1$となる。

初期化

隣り合う塩基同士は結合しないため、次のように初期化する。

\displaylines{
M(i,i-1) = 0 \quad (i=2,\dots,n \ のとき) \\
M(i,i) = 0 \quad (i=1,\dots,n \ のとき)
}

動的計画法の再帰式

以下の再帰式をもとに、$M(1,n)$を計算する。

M(i,j) = \max \ \left\{
\begin{array}{lll}
M(i+1,j) \\
M(i,j-1) \\
M(i+1,j-1) + Score(i,j)
\end{array}
\right.

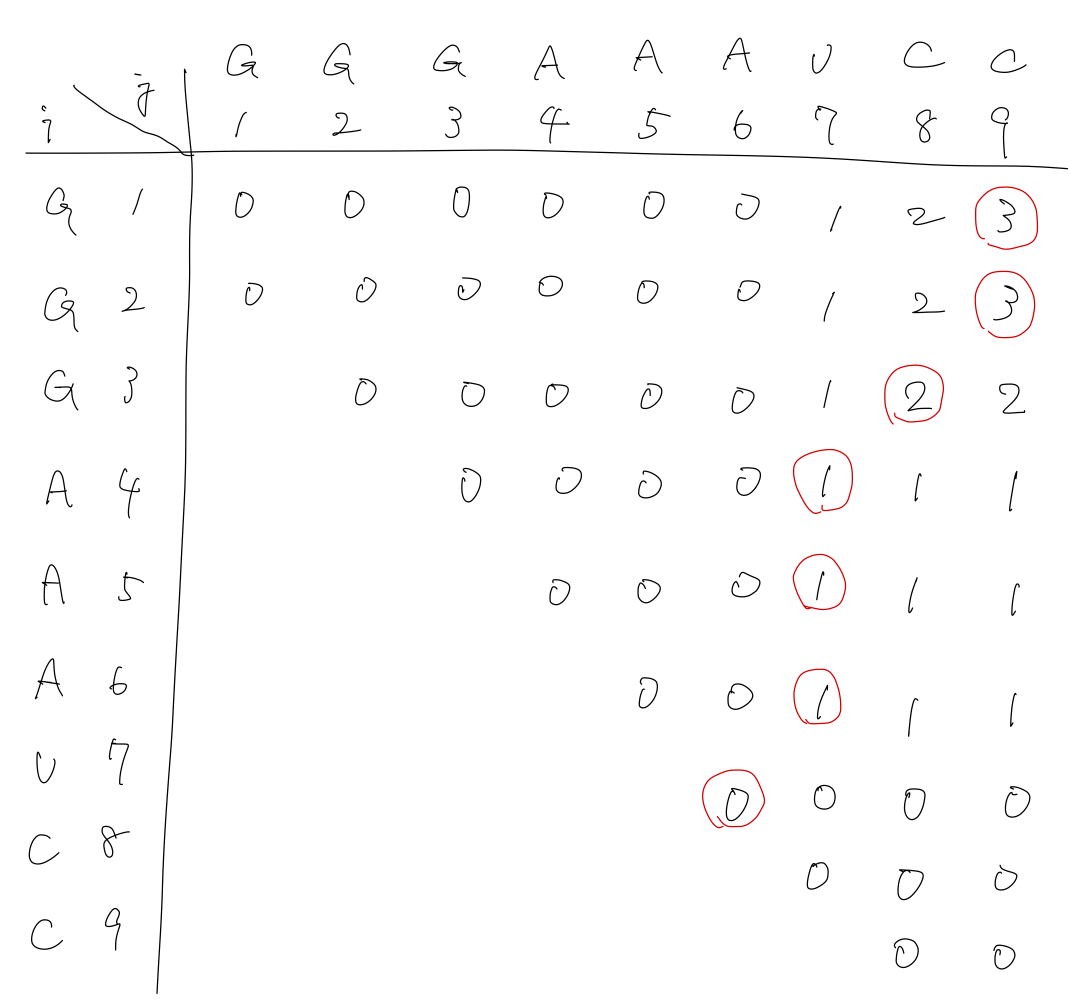
Nussinovアルゴリズム計算表

例として長さ $n=9$ の塩基配列 GGGAAAUCC について、Nussinovアルゴリズムを用いて、とりうる構造における最大のペア数を計算する。初期化したあと、$M(1,3),M(2,4),M(3,5),\dots$と順に計算していき、$M(1,9)$を求める

実装

標準入力から配列をうけとり、最大ペア数を返すプログラムを書きました。

nussinov.go

package main

import (
	"bufio"
	"fmt"
	"os"
	"strings"
)

func main() {
	sequence := readSequence()
	if sequence == "" {
		fmt.Fprintln(os.Stderr, "Invalid input. One line of RNA sequence expected.")
		os.Exit(1)
	}

	fmt.Println(maxPairs(sequence))
}

// Nussinov アルゴリズムを実行し、指定された配列の最大ペア数を返す
func maxPairs(seq string) int {
	n := len(seq)
	if n == 0 {
		return 0
	}

	M := make([][]int, n)
	for i := range M {
		M[i] = make([]int, n)
	}

	for l := 1; l < n; l++ {
		for i := 0; i+l < n; i++ {
			j := i + l // 塩基iとjの区間長はl

			score := 0
			if canPair(seq[i], seq[j]) {
				score = 1
			}

			M[i][j] = max(M[i+1][j], M[i][j-1], M[i+1][j-1]+score)
		}
	}

	return M[0][n-1]
}

// 塩基対を形成するか
func canPair(a, b byte) bool {
	return (a == 'A' && b == 'U') ||
		(a == 'U' && b == 'A') ||
		(a == 'G' && b == 'C') ||
		(a == 'C' && b == 'G')
}

// 文字列の整形
func normalize(s string) string {
	return strings.ToUpper(strings.TrimSpace(s))
}

// 読み込み
func readSequence() string {
	fmt.Print("Input RNA: ")
	scanner := bufio.NewScanner(os.Stdin)
	if scanner.Scan() {
		return normalize(scanner.Text())
	}
	return ""
}