まえがき
本記事は”制御工学 Advent Calendar 2017”の12/21の記事として書きました.
内容について理解しているとは言い難いので,間違いについてはどんどんコメントいただければ幸いです.
本記事ではMadgwickフィルタの論文を読んだので,それについて一部を日本語でまとめたものです.原論文”An efficient orientation filter for inertial and inertial/magnetic sensor arrays”では,ジャイロセンサと加速度センサを用いた場合とさらにそれに地磁気センサを加えた場合についても論じておりますが,今回はジャイロセンサと加速度センサのみの場合について書きました.地磁気を導入した場合も基本原理はあまり変わらないようです.
クォータニオンベースのフィルタですが,クォータニオンに関しては別途文献を参照ください.本記事は原論文を読む前にざっくりと概要をつかむのに役に立てば幸いです.また,実際のコードも原論文にありますので,そちらをご覧になった方が早いかもしれません.
参考文献については,原論文のみですので,参照番号等は省略いたします.以下の式番号は全て原論文の物を流用しておりますので,式番号がとびとびの部分が有ります.
Madgwickフィルタとは
詳しくは,原論文を読んだ方が圧倒的に早いので,ざっくりと説明します.
Madgwickさんが提唱されたもので,カルマンフィルタに比べて、高速で同程度以上の精度を実現したらしいフィルタです.カルマンフィルタがモデルの構造が不明な場合に高精度を実現するのが難しいのに対して,Madgwickフィルタは同程度の精度を実現しながら高速に処理が可能なフィルタです.一方で,少し調べた範囲ですと,収束が遅いらしいとか・・・?
なによりもの最大のメリットは,その処理速度です.マイコン(RX631@100MHz)で実行時に実測で$200\mu$程度で処理を実現できています.
3.フィルタの導出
3.0クォータニオンの基本表現
クォータニオンの表記として,
^A_B\hat{q}=[q_1,q_2,q_3,q_4]=[cos\frac{\theta}{2},-r_x sin\frac{\theta}{2}, -r_y sin\frac{\theta}{2},-r_z sin\frac{\theta}{2}]\cdots(1)
これは,フレームAに対するフレームBの向きを表わします.
また,共役クォータニオンを
^A_B\hat{q}^*=^B_A\hat{q}=[q_1,-q_2,-q_3,-q_4]\cdots(2)
としています.
次に,2つのクォータニオンの積については,$\otimes$を使って表記します.$^A_B\hat{q}$と$^B_C\hat{q}$の積は,
^A_C\hat{q} = ^B_C\hat{q} \otimes ^A_B\hat{q}\cdots(3)
となり,フレームAからフレームCへの向きを表わします.
[](
これは,位置ベクトルの回転のことを話しているのかな?/
座標系の回転と位置ベクトルの回転って何が違うの?
)
ここで,実際に$\otimes$は,
{\bf{a}} \otimes {\bf{b}} =[a_1, a_2, a_3, a_4]\otimes [b_1,b_2,b_3,b_4]\\
=\begin{bmatrix}
a_1 b_1 - a_2 b_2 - a_3 b_3 -a_4 b_4\\\
a_1 b_2 - a_2 b_1 + a_2 b_1 + a_3 b_4 - a_4 b_3\\\
a_1 b_3 - a_2 b_4 + a_3 b_1 + a_4 b_2 \\\
a_1 b_4 +a_2 b_3 -a_3 b_2 +a_4 b_1]
\end{bmatrix}
\cdots(4)
となります.
次に,三次元ベクタのクォータニオンによる回転は,
^B{\bf{v}} = ^A_B\hat{q} \otimes ^A{\bf{v}} \otimes ^A_B\hat{q}^* \cdots(5)
として表わされます.ここで,右辺では三次元ベクタの先頭要素に0が挿入され計算されます.
$^A{\bf{v}} = [a,b,c]$
の時に,
$[0,a,b,c]$
と拡張され右辺が計算されます.
原論文ですとクォータニオンから回転行列への変換が少し説明されていますが省略します.
3.1角速度からの姿勢計算
まず,センサーフレームでの角速度を,
^S\omega=[0 ,\omega_x,\omega_y,\omega_z] [rad/s]\cdots(10)
とします.
また,アースフレームからセンサーフレームへのクォータニオンによる回転の時間微分は,
^S_E\dot{q}=\frac{1}{2}^S_E\hat{q}\otimes^S\omega\cdots(11)
と計算されます.
次に離散時間で考えると,時刻tにおける姿勢クォータニオンを$^S_Eq_{\omega,t}$,t-1における推定値を$^S_E\hat{q}_{est,t-1}$として,
^S_E\dot{q}_{\omega,t}=\frac{1}{2}^S_E\hat{q}_{est,t-1}\otimes^S\omega_t\cdots(12)
^S_Eq_{\omega,t}=^S_E\hat{q}_{\omega,t-1} + ^S_E\dot{q}_{\omega,t}\Delta t\cdots(13)
となります.
3.2計測ベクタからの姿勢表現
加速度センサが計測する値は,センサーフレームでの重力加速度とセンサーフレームのモーションによって生じる加速度の複合されたものである.しかし,ここでは,重力加速度のみ計測されるとした.(地磁気も同様な感じ)
その上で,アースフレームでその真値が分かっているならば,センサーフレームで計測されるであろう値を姿勢クォータニオンから計算できるはずであり,2つのベクトルの差分を求めることもできる.そしてその差分がもっとも小さくなる姿勢クォータニオン$^S_E\hat{q}$が最も適切な姿勢であるはずであるので,
min(^S_E\hat{q}\in R^4) {\bf{f}}(^S_E\hat{q},^E\hat{d},^S\hat{s})\cdots(14)\\\
{\bf{f}}(^S_E\hat{q},^E\hat{d},^S\hat{s}) = ^S_E\hat{q}^*\otimes ^E\hat{d} \otimes ^S_E\hat{q} - ^S\hat{s}\cdots(15)\\\
^S_E\hat{q}=[q_1,q_2,q_3,q_4]\cdots(16)\\\
^E\hat{d}=[0, d_x,d_y,d_z]\cdots(17)\\\
^S\hat{s}=[0,s_x,s_y,s_z]\cdots(18)
[](
これセンサーフレームからアースフレームへのクォータニオンの共役をとることで,アースフレームからセンサーフレームを計算している?
座標系の回転になるのかな?
)
この最適化問題にたいするアルゴリズムとして,最急降下法(gradient descent algorithm)を採用する.
このアルゴリズムは次の4つの式で説明される.
^S_E{q}_{k+1}=^S_E\hat{q}_k -\mu\frac{\nabla{\bf{f}}(^S_E\hat{q}_k,^E\hat{d},^S\hat{s})}{||\nabla{\bf{f}}(^S_E\hat{q}_k,^E\hat{d},^S\hat{s})||},k=0,1,2\dots n \cdots(19)\\\
\nabla{\bf{f}}(^S_E\hat{q}_k,^E\hat{d},^S\hat{s})={\bf{J}}^T(^S_E\hat{q}_k,^E\hat{d}) {\bf{f}}(^S_E\hat{q}_k,^E\hat{d},^S\hat{s}) \cdots(20)\\\
{\bf{f}}(^S_E\hat{q}_k,^E\hat{d},^S\hat{s})=
\begin{bmatrix}
2d_x(\frac{1}{2}-q_3^2-q_4^2)+2d_y(q_1q_4+q_2q_3)+2d_z(q_2q_4-q_1q_3)-s_x\\\
2d_x(q_2q_3-q_1q_4)+2d_y(\frac{1}{2}-q_2^2-q_4^2)+2d_z(q_1q_2+q_3q_4)-s_y\\\
2d_x(q_1q_3+q_2q_4)+2d_y(q_3q_4-q_1q_2)+2d_z(\frac{1}{2}-q_2^2-q_3^2)-a_z
\end{bmatrix} \cdots(21)\\\
{\bf{J}}^T(^S_E\hat{q}_k,^E\hat{d})=
\begin{bmatrix}
2d_yq_4-2d_zq_3 & 2d_yq_3+2d_zq_4 & -4d_xq_32d_yq_2-2d_zq_1 & -4d_xq_4+2d_yq_1+2d_zq_2\\\
-2d_xq_4+2d_zq_2 & 2d_xq_3-4d_yq_2+2d_zq_1 & 2d_xq_2+2d_zq_4 & -2d_xq_1-4d_yq_4+2d_zq_3\\\
2d_xq_3-2d_yq_2 & 2d_xq_4-2d_yq_1-4d_xq_2 & 2d_xq_1+2d_yq_4-4d_zq_3 & 2d_xq_2+2d_yq_3
\end{bmatrix} \cdots(22)
この説明についても原論文にはありますが,省略します.
その上で,加速度センサを利用する場合を考えると,計測値を正規化したものとし,
^E\hat{g}=[0, 0, 0, 1]\cdots(23)\\\
^S\hat{a}=[0,a_x, a_y ,a_z]\cdots(24)
と表わされる.これを前述した式に代入すると,
{\bf{f}}_g(^S_E\hat{q},^S\hat{a})=
\begin{bmatrix}
2(q_2q_4-q_1q_3)-a_x\\\
2(q_1q_2+q_3q_4)-a_y\\\
2(\frac{1}{2}-q_2^2 -q_3^2)-a_z
\end{bmatrix}
\cdots(25)\\\
{\bf{J}}_g(^S_E\hat{q})=
\begin{bmatrix}
-2q_3 & 2q_4 & -2q_1 & 2q_2 \\\
2q_2 & 2q_1 & 2q_4 & 2q_3 \\\
0 & -4q_2 & -4q_3 &0
\end{bmatrix} \cdots(26)
よって,最終的な更新式は,
^S_Eq_{\nabla,t}=^S_Eq_{est,t-1}-\mu_t \frac{\nabla{\bf{f}}}{||\nabla{\bf{f}}||} \cdots(33)
地磁気の場合も同様の議論で式を得ることができる.原論文では,それらを複合した式を最終的に求めているが今回は省略した.
ここで式中の$\mu_t$の最適値は$^S_Eq_{\Delta,t}$の収束率として定義できる.これは,不必要に大きなステップサイズに起因するオーバーシュートを回避するために,物理的な姿勢変化速度(physical orientation rate)によって制限される.そのため,$\Delta t$をサンプリング時間として,$^S_E\dot{q}_{\omega ,t}$をジャイロセンサによる計測値,$\alpha$を加速度センサのノイズによって決まる値として,
\mu_t = \alpha || ^S_E\dot{q}_{\omega ,t}|| \Delta t , \alpha > 1\cdots(35)
3.3フィルタフュージョンアルゴリズム
ここでは,フィルタフュージョンアルゴリズムについて説明しています.
地磁気を使わない場合の説明は比較的少なかったので,読みやすいと思います.
最終的な推定値${^S_E\hat{q_{est,t}}}$は,角速度から計算された$^S_E\hat{q_{\omega,t}}$と3.2までで説明してきた式から計算された$^S_E\hat{q_{\nabla,t}}$のフュージョンとして計算する.各姿勢クォータニオンに対する重みの変数として,$\gamma _t$を撮ると,
^S_E{q}_{est,t} = {\gamma_t} ^S_E{q}_{\nabla,t} + (1-\gamma_t)^S_E{q}_{\omega,t} , 0\leq \gamma_t \leq 1\cdots(36)
として計算する.
ここで適切な重みはジャイロセンサによる姿勢の発散の重みと加速度センサによる姿勢の収束の重みが等しいことによって,定義できる.加速度センサによる姿勢$^S_E{q_{\nabla,t}}$の収束率は$\frac{\mu_t}{\Delta t}$であり,$\beta$をジャイロセンサの計測誤差によるクォータニオンに微分の大きさとして表わされる$^S_E{q}_{\omega,t}$を発散率として,
(1-\gamma_t)\beta = \gamma_t \frac{\mu_t}{\Delta t}\cdots(37)
よって,
\gamma_t=\frac{\beta}{\frac{\mu_t}{\Delta t}+\beta}\cdots(38)
となる.
ここで,$\alpha$に上限が無く,$\mu_t$にたいして非常に大きいと仮定すると,式(33)の$^S_E\hat{q}_{est,t-1} $は無視でき,
^S_E{q}_{\nabla,t}\approx -\mu_t \frac{\nabla {\bf{f}}}{||{\bf{f}}||}\cdots(39)
として近似できる.
同様に式(38)の分母の$\beta$も無視できるので,
\gamma_t \approx \frac{\beta \Delta t}{\mu_t}\cdots(40)
となり,式(40)を$\gamma_t \approx 0$と近似可能である.
以上の式(13),(39),(40)を(36)に代入することで,式(41)を得られる.
^S_Eq_{est,t}=\frac{\beta \Delta t}{\mu_t}(-\mu_t \frac{\nabla {\bf{f}}}{||\nabla {\bf{f}}||})+(1-0)(^S_E\hat{q}_{est,t-1}+^S_E\dot{q}_{\omega,t}\Delta t) \cdots(41)
よって,式(41)から最終的にフィルタの更新式は,(42),(43),(44)で与えられる.
^S_Eq_{est,t} = ^S_E\hat{q}_{est,t-1}+^S_E\dot{q}_{est,t}\Delta t \cdots(42)\\\
^S_E\dot{q}_{est,t} = ^S_E\dot{q}_{\omega,t}-\beta ^S_E\dot{\hat{q}}_{\epsilon,t} \cdots(43)\\\
^S_E\dot{\hat{q}}_{\epsilon,t}= \frac{\nabla {\bf{f}}}{||{\bf{f}}||} \cdots(44)
以上が,フィルタフュージョン部分である.
このあとに原論文では地磁気についての考察が進められているが,省略します.
ここまでが,論文を読んだ範囲での自分なりの理解の一つの区切りです.
MatlabによるMadgwick Filter の検証
ということで,ここまでのアルゴリズムを実際のセンサで取得した値に適応して効果を見てみたいと思います.C言語のコードは論文の末尾に有りましたので,今回はMATLABで実現してみます.センサはMPU9250を用い,計測周期1kHz,各種フィルタ機能はオフに設定しました.計測時間は25secとして,適当に手で動かしたときのデータです.
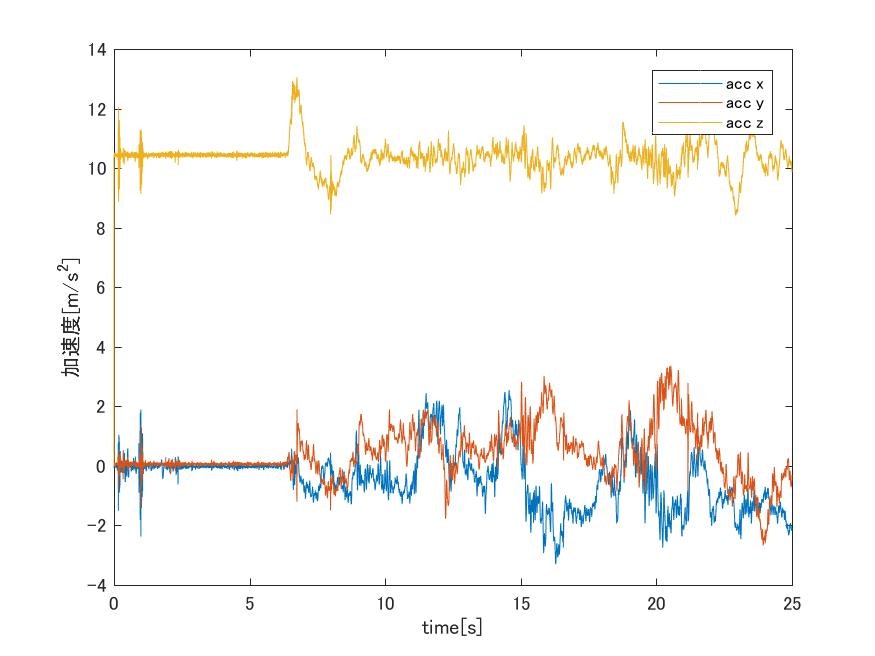
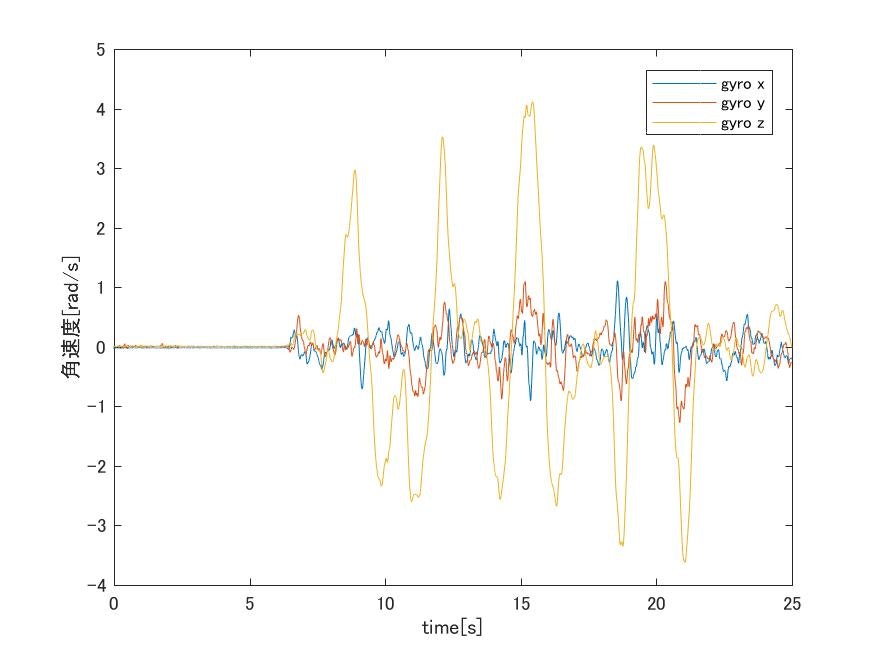
まず,ジャイロセンサと,加速度センサの生のデータをそれぞれ以下に図として示します.
ここにIMUの生データ
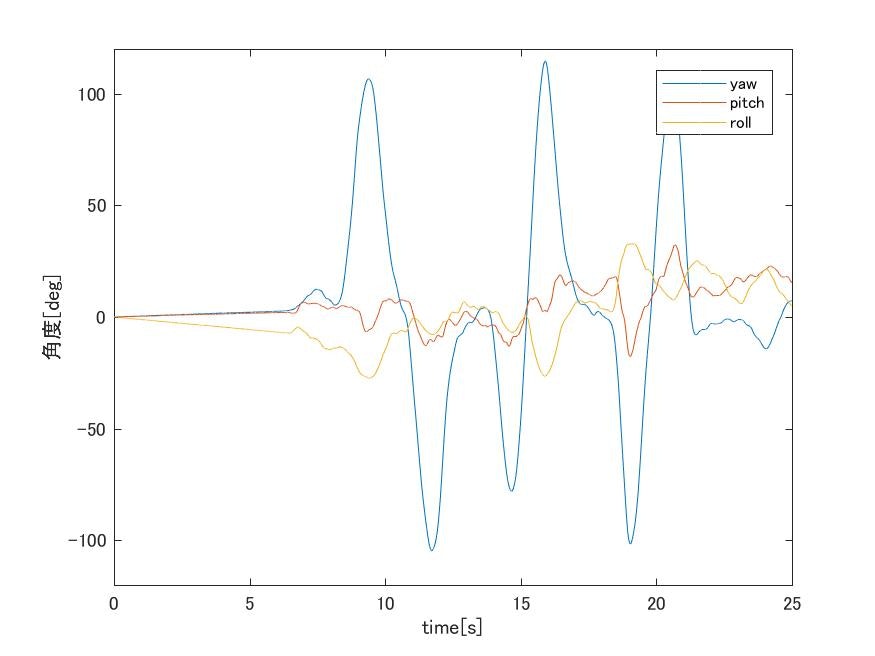
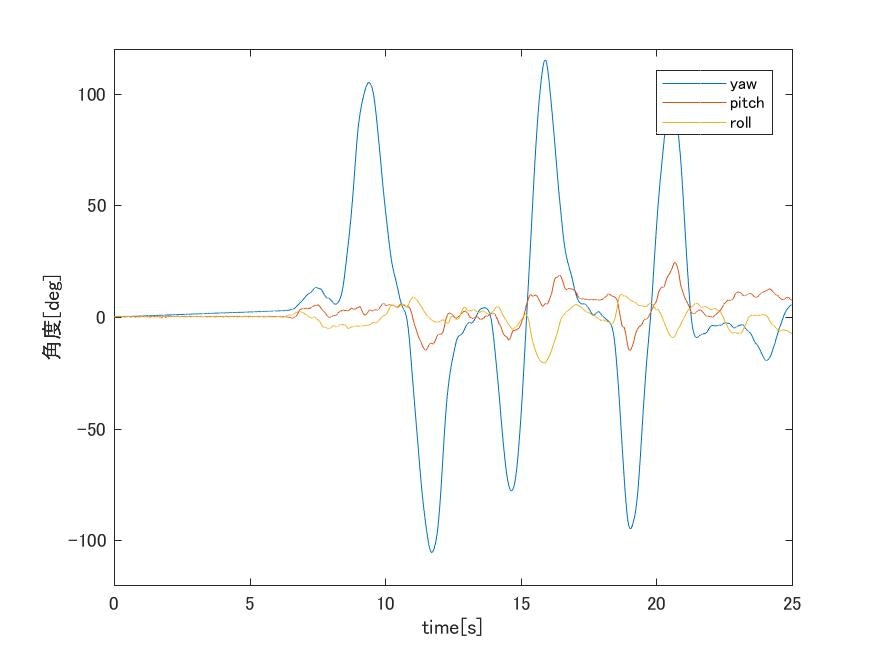
次に,ジャイロセンサによる角速度のみを積分して求めたヨー・ピッチ・ロール角度とMadgwickフィルタを利用して求めたものを以下に図として示します.
ここにyprデータ
以上のようにジャイロセンサのみではピッチ、ロール角がドリフトしているのにたいして,Madgwickフィルタを用いることで抑制できていることが確認できます.一方で,地磁気を用いていないため,ヨー角はドリフトが生じています.
さいごに
実際に記事を書いてみて,自分の理解の浅さがどんどんと身に染みてくるものでした.結構な部分が自身でも理解があやふやなため,お読みいただいた方にはぜひとも原論文を読んでいただければと思います.
以下に使用したMatlabコードを参考の貼り付けます.
clear all;
close all;
% データ読み込み
load('data_imu_20171220_8.mat');
imu_acc=mpu_data(:,1:3);
imu_gyro=mpu_data(:,4:6);
Ts_imu=1e-3; %サンプリング間隔
N_imu=length(imu_gyro);
t=0:Ts_imu:(N_imu -1) *Ts_imu;
q = [1 0 0 0]; %初期クォータニオン
figure('Name','IMU Acc');
plot(t,imu_acc); legend('acc x','acc y','acc z');
ylabel('加速度[m/s^2]');xlabel('time[s]');
saveas(gcf,'imu_acc.jpg');
figure('Name','IMU Gyro');
plot(t,imu_gyro);legend('gyro x','gyro y','gyro z');
ylabel('角速度[rad/s]');xlabel('time[s]');
saveas(gcf,'imu_gyro.jpg');
% もっとも単純なジャイロセンサの積分(クォータニオン空間)
for i=2:N_imu
imu_quatlized = [0 imu_gyro(i,:)
-imu_gyro(i,1) 0 -imu_gyro(i,3) imu_gyro(i,2)
-imu_gyro(i,2) -imu_gyro(i,3) 0 -imu_gyro(i,1)
-imu_gyro(i,3) imu_gyro(i,2) imu_gyro(i,1) 0];
q(i,:)=q(i-1,:) + (1/2).* q(i-1,:) * imu_quatlized .* Ts_imu;
q(i,:) = q(i,:)./norm(q(i,:));
end
[pitch, roll , yaw] = quat2angle(q,'YXZ');
deg_pitch = rad2deg(pitch);
deg_roll = rad2deg(roll);
deg_yaw = rad2deg(yaw);
figure('Name','IMU gyro only');
plot(t,[deg_yaw';deg_pitch';deg_roll']');
ylim([-120,120]);
legend('yaw','pitch','roll');
ylabel('角度[deg]');xlabel('time[s]');
saveas(gcf,'only_gyro.jpg');
% ここからMadgwickフィルタを実装する
% q_mad=q(1,:);
q_mad = q;
beta = sqrt(3/4)*pi*(5.0/180.0);%原論文のまま
for i=2:N_imu
% 加速度センサの正規化
acc_norm=imu_acc(i,:)./ norm(imu_acc(i,:));
% J,\nabla{f}の計算
f_g=[(2*(q_mad(i-1,2)*q_mad(i-1,4)-q_mad(i-1,1)*q_mad(i-1,3)) - acc_norm(1))...
(2*(q_mad(i-1,1)*q_mad(i-1,2)+q_mad(i-1,3)*q_mad(i-1,4)) -acc_norm(2))...
(2*(1/2 - q_mad(i-1,2)^2 - q_mad(i-1,3)^2) - acc_norm(3))]';
J_g=[-2*q_mad(i-1,3) 2*q_mad(i-1,4) -2*q_mad(i-1,1) 2*q_mad(i-1,2)
2*q_mad(i-1,2) 2*q_mad(i-1,1) 2*q_mad(i-1,4) 2*q_mad(i-1,3)
0 -4*q_mad(i-1,2) -4*q_mad(i-1,3) 0];
nabla_f = J_g'*f_g;
% 式(44)の計算
q_ep=nabla_f ./ norm(nabla_f);
% 式(43)の計算
imu_quatlized = [0 imu_gyro(i,:)
-imu_gyro(i,1) 0 -imu_gyro(i,3) imu_gyro(i,2)
-imu_gyro(i,2) -imu_gyro(i,3) 0 -imu_gyro(i,1)
-imu_gyro(i,3) imu_gyro(i,2) imu_gyro(i,1) 0];
q_dot_t_omega = (1/2).* q_mad(i-1,:) * imu_quatlized;
q_dot_est = q_dot_t_omega - beta * q_ep';
% 式(42)の計算
q_mad(i,:)=q_mad(i-1,:) + q_dot_est .* Ts_imu;
end
[pitch, roll , yaw] = quat2angle(q_mad,'YXZ');
deg_pitch = rad2deg(pitch);
deg_roll = rad2deg(roll);
deg_yaw = rad2deg(yaw);
% Madgwcik
figure('Name','IMU Madgwick');
plot(t,[deg_yaw';deg_pitch';deg_roll']');
ylim([-120,120]);
legend('yaw','pitch','roll');
ylabel('角度[deg]');xlabel('time[s]');