ふくだ学習録とは？

ふくだが学習したことの備忘録。
目に見える形で残すことによってやる気を出す個人的な作戦です。
他人に見せるように書いているわけではないので、すごく読みにくいです。

読了した本

データベースエンジニア養成読本 [DBを自由自在に活用するための知識とノウハウ満載!]

ゼロから作るDeepLearningを読んで

ブロードキャストとは？

NumPyで、n次元配列に対して、スカラ値（行列でない単なる数値）を四則演算することができることを「ブロードキャストできる」という。
実際には、NumPyがスカラ値を適当なn次元配列だと拡大解釈してくれルことにより、計算できるようにしてくれている。

np.arrayでのfor文の書き方

for row in 行列と記載する。

example

>>> X = np.array([[1, 2], [3, 4]],[5, 6])

>>> for row in X:
        print(X)
[1 2]
[3 4]
[5 6]

NumPyのパフォーマンスに関して

NumPyはPythonで記載するが、主な処理はC/C++で実装されている。
そのため計算が早い。

matplotlibとは？

グラフの描画を行うためのライブラリ。
Anacondaなどには最初から入っている。

パーセプトロンとは？

ニューラルネットワーク（ディープラーニング）の起源となるアルゴリズム。
複数の信号を入力として受け取り、ひとつの信号を出力するもの。複数のニューロンよって構成されている。
パーセプトロンの信号は「流す/流さない（1か０）」の二値の値となっている。

入力された値は、各ニューロンで重み付けされた上で、次のニューロンに送信される。
最終的なニューロンが受け取った値の総和が一定数以上の場合に、発火して「１」と出力する。

閾値（しきい値）とは？

パーセプトロンが発火するかしないかの臨界点の数値のこと。
（発火する限界値）

ANDゲートとNANDゲートの関係性

ANDゲートのパラメータの符号を全て反転させることで、NANDゲートのパラメータを作成することができる。（まぁそりゃそう）

Pythonでの重み付け、バイアスの掛け方

簡単な入力値、重み、バイアスを使ったパーセプトロンの実装方法は下記になる。

AND

def AND(x1, x2):
    x = np.array([x1, x2])    #入力値
    w = np.array([0.5, 0.5])  #重み
    b = -0.7                  #バイアス
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

NAND

def NAND(x1, x2):
    x = np.array([x1, x2])      #入力値
    w = np.array([-0.5, -0.5])  #重み　   ←ここがANDと違う
    b = 0.7                     #バイアス  ←ここがANDと違う
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

def OR(x1, x2):
    x = np.array([x1, x2])    #入力値
    w = np.array([0.5, 0.5])  #重み
    b = -0.2                  #バイアス  ←ここがANDと違う
    tmp = np.sum(w*x) + b
    if tmp <= 0:
        return 0
    else:
        return 1

np.arrayを用いたら、入力値と重みの乗算が表現しやすくなるのか…
なるへそ。

XORゲートとは？

排他的論理和のこと。
AとB、どちらか片方だけが1の時に１を返す。

A=１　B=1 →　０
A=０　B=０ →　０
A=１　B=０ →　１
A=０　B=１ →　１

前述していたパーセプトロンの構造ではXORを実現することは難しい。
なぜなら、さっきまでのパーセプトロンの構成（関数表現）では、一次関数しか表現できず、XORは一次関数では表現ができないから。
これに対して、パーセプトロンの層を重ねることで解決していく。

XORの関数表現

XORはAND、NAND、OR関数を組み合わせることで表現できる。
実際の表現方法は下記。

XOR

def XOR(x1, x2):
    s1 = NAND(x1, x2)
    s2 = OR(x1, x2)
    y = AND(s1, s2)
    return y

上記したXOR関数をニューロンの層で考えると、多層になっている。（XORでは２層）
そのように層を複数個重ねたパーセプトロンを多層パーセプトロンと呼ぶ。

パーセプトロンの欠点

欠点というか「こうなったらいいのに！」って部分。
パーセプトロンでは、重みを設定する部分が人の手によって行われてしまっている。
（さっきのAND、NAND、OR関数でいうwの部分）
その「適切な重み付けを人が行わなくてはならない」という問題点を解決するために考えられたのが、ニューラルネットワーク。

ステップ関数とは？

閾値を境にして出力が切り替わる（０から１になる）活性化関数のこと。階段関数とも呼ばれる。
パーセプトロンには、活性化関数としてステップ関数が使用されている、

シグモイド関数とは？

ニューラルネットワークで、活性化関数として使用される関数。

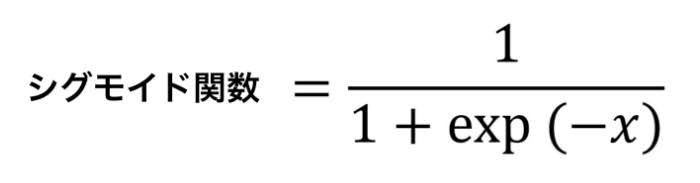
※eはネイピア数というもの（e=2.7182... ）
exp(-x)はeの-x乗のこと。

活性化関数には、線形関数を使用してはならない

線形関数を何層にしても、それを代替する関数が存在してしまう　＝　複数層にする意味がなくなる　から。

ReLU関数とは？

入力が０を超えていれば、入力をそのまま出力し、
入力が０以下であれば、０を出力する関数。

Pythonでの多次元配列の扱い方

NumPyを使用する。

ndim()

>>> import numpy as np
>>> A = np.array([1, 2, 3, 4])
>>> print(A)
[1 2 3 4]

>>> np.ndim(A)
1

>>> A.shape
(4,)

>>> A.shape[0]
4

行列の積

dot()

>>> import numpy as np
>>> A = np.array([[1, 2],
                  [3, 4]])
>>> A.shape
(2, 2)

>>> B = np.array([[5, 6],
                  [7, 8]])
>>> B.shape
(2, 2)

>>> np.dot(A, B)
array([[19, 22],
       [43, 50]])

※np.dot(A, B)とnp.dot(B, A)は違う値になり得る。

今日の一言

今のところ、もともと知ってた部分が多いので、あんまりメモない&スイスイ進む。
明日からはニューラルネットワークの概念の学習入るけど、早く実践に入りたいー。
けど基礎固め重要やから読み飛ばさずに進む。鬼眠い！

【ふくだ学習録】ゼロから作るDeepLearning part2【7日目】