データ構造とアルゴリズムをなぜ学ぶべきか
あるデータを探索して取得したいとか、この大量のデータをソートしたいとかなった時に、既存の関数を使うのも良いけど、データの構造やその都度のデータ量を考慮して、最適なアルゴリズムを取捨選択できるようになっていた方がいいよねといった形のフィードバックを、最近就活時の面接時に頂いて、なるほどね〜と思いつつ、やってみた所存。まだまだ、学んでいる途中ですので、今後追記していきます。
サーチアルゴリズム
いわば探索アルゴリズムですよね。配列中から、指定した値があるかどうか探索するアルゴリズムです。
リニアサーチ
一番シンプルなアルゴリズムで、配列中から指定した値を先頭から順に一致するかどうか検証して、一致したもののインデックスを返す仕様です。
def linear_search(searchArr,searchNum)
index = 0
count = 0
searchArr.each do |arr|
if arr == searchNum
count += 1
else
index += 1
end
end
if count == 0
puts "value:#{searchNum} Array:#{searchArr} There isn't it."
else
puts "value:#{searchNum} Array:#{searchArr} There is it at index\s#{index}."
end
end
メリット
下記の通り、先頭から順に要素を探索するだけなので、実装が容易である。
デメリット
先頭から1個ずつ探索する故に、かなり速度が落ちる。
バイナリサーチ
中央の要素を取得して、探索したい値がそれより大きいか小さいかを比較して、検証する要素を右や左に移しつつ、探索するアルゴリズムです。少し複雑ですので、手順を紹介します。
手順
1.配列をソートする。(昇順でも降順でも可能)
2.配列の中央にある要素を目的の要素と比較する。
3.中央の要素が、目的の要素より大きければ、中央より後半を探索。
4.そうではない場合は、前半を探索する。
def binary_search(array,searchNum)
array.sort!
leftIndex = 0
rightIndex = array.index(array.last)
midIndex = (rightIndex + leftIndex) / 2
loop do
if searchNum == array[midIndex]
puts "Array->#{array}:There is it at #{midIndex}!"
break;
elsif searchNum > array[midIndex]
midIndex += 1
else
midIndex -= 1
end
end
end
メリット
リニアサーチは、先頭の要素から探索するのに対して、バイナリサーチは、ソート→中央の値を比較するという手順で、より速度が上がる。
デメリット
ソートする手順を踏む必要があるので、要素が「数値」である必要がある。
速度を比較してみた
benchmarkというライブラリを使って比較してみます。
require 'benchmark'
def linear_search(array_size,searchNum)
array = (1..array_size).to_a
index = 0
count = 0
array.each do |arr|
if arr == searchNum
count += 1
else
index += 1
end
end
if count == 0
# puts "value:#{searchNum} Array:#{array} There isn't it."
else
# puts "value:#{searchNum} Array:#{array} There is it at index\s#{index}."
end
end
def binary_search(array_size,searchNum)
array = (1..array_size).to_a
array.sort!
leftIndex = 0
rightIndex = array.index(array.last)
midIndex = (rightIndex + leftIndex) / 2
loop do
if searchNum == array[midIndex]
# puts "Array->#{array}:There is at #{midIndex}!"
break;
elsif searchNum > array[midIndex]
midIndex += 1
else
midIndex -= 1
end
end
end
p "---100 elements---"
puts Benchmark.measure{linear_search(100,50)}
puts Benchmark.measure{binary_search(100,50)}
p "---1000 elements---"
puts Benchmark.measure{linear_search(1000,100)}
puts Benchmark.measure{binary_search(1000,100)}
p "---10000 elements---"
puts Benchmark.measure{linear_search(10000,1000)}
puts Benchmark.measure{binary_search(10000,1000)}
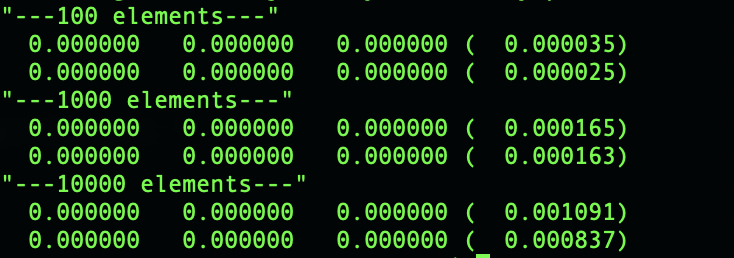
結果
ソートアルゴリズム
要素である数値を昇順、降順に並べるアルゴリズムです。
バブルソート
バブルソートは、そのソートの動きから由来しているそうです。やってみます。
手順
1.先頭の要素を1,その次の要素を2とします。まず、1と2を比較します。1の方が2より小さければ交換せず、そのまま、2の要素を1として、2の要素の次の要素を2として、同じように比較します。(つまり、比較する要素同士を右に移行します。)
2.隣り合う要素を比較して、1より2の要素の方が大きければ、要素を交換してあげます。そして上記のように、比較する要素同士を右に移行して同じように比較します。
3.1,2を繰り返します。
def bubble_sort(array)
arrayLength = array.length
for length in 1..arrayLength
for nextIndex in 1..(arrayLength - length)
if array[nextIndex-1] > array[nextIndex]
t = array[nextIndex-1]
array[nextIndex-1] = array[nextIndex]
array[nextIndex] = t
end
end
end
p array
end
メリット
実装がかなり容易でかつ、わかりやすい。
デメリット
要素同士をスワップしながら、ソートしていくので、大量のデータをソートするので速度は落ちる。
選択ソート
ループ中に発見した最小値を予め変数に記憶しておくやり方で、ループ回数を抑えられるソートです。
手順
1.先頭の要素を仮の最小値として指定する。
2.次の要素から、1個ずつ比較していき、仮の最小値より小さい値があるとき、そのインデックスを記憶しておく。
3.さらに次の要素→次の要素と比較して、更に小さい値があれば、先ほどインデックスを記憶しておいた変数を更新する。更新した変数が最小値だった場合、先頭の要素とスワップする。
4.0番目の要素の仮最小値としての1,2,3の検証が終了したら、1番目の要素にずらして、1,2,3を繰り返す。
def selection_sort(array)
len = array.length
0.upto(len-2).each do |i| #検証回数
minIndex = i #仮最小値設定
(i+1).upto(len-1).each do |j| #検証要素範囲
minIndex = j if array[j] < array[minIndex] #最小値を随時記憶→更新
end
if i != minIndex
temp = array[minIndex]
array[minIndex] = array[i]
array[i] = temp
p array
#現在の仮最小値でない場合SWAP
end
end
return array
end
メリット
バブルソートに比べて交換する手順が1回だけで抑えられるので、若干バブルソートに比べて速度が上がります。
速度を比較してみた
require 'benchmark'
def bubble_sort(array)
arrayLength = array.length
for length in 1..arrayLength
for nextIndex in 1..(arrayLength - length)
if array[nextIndex-1] > array[nextIndex]
t = array[nextIndex-1]
array[nextIndex-1] = array[nextIndex]
array[nextIndex] = t
end
end
end
return array
end
def selection_sort(array)
len = array.length
0.upto(len-2).each do |i|
minIndex = i
(i+1).upto(len-1).each do |j|
minIndex = j if array[j] < array[minIndex]
end
if i != minIndex
temp = array[minIndex]
array[minIndex] = array[i]
array[i] = temp
end
end
return array
end
p "---100 elements---"
puts Benchmark.measure{bubble_sort((1..100).to_a.shuffle)}
puts Benchmark.measure{selection_sort((1..100).to_a.shuffle)}
p "---1000 elements---"
puts Benchmark.measure{bubble_sort((1..1000).to_a.shuffle)}
puts Benchmark.measure{selection_sort((1..1000).to_a.shuffle)}
p "---10000 elements---"
puts Benchmark.measure{bubble_sort((1..10000).to_a.shuffle)}
puts Benchmark.measure{selection_sort((1..10000).to_a.shuffle)}
結果
参考記事
下記のリンクのサイトでは、動きでアルゴリズムがわかるようになっていて非常に理解しやすいです。是非使ってみてください。
https://visualgo.net/ja
Qiita参考
https://qiita.com/fukumone/items/5a0c0964f2c713b0699d
1週間で学ぶデータ構造とアルゴリズム
http://sevendays-study.com/algorithm/index.html