Rustじゃなくて、数学に挫折した（Canvas上での）コッホ曲線描画（途中まで）

数学がわかりません。
三角関数がわかりません。

そんな状態でRustのWebAssemblyでコッホ曲線を描画しようとしました。

書籍「RustとWebAssembleによるゲーム開発」を見ながら、RustでのWebAssembleによるCanvas描画を覚え、シェルピンスキーの三角形を描きました。

それを真似して、別のフラクタルを描こうと思い、コッホ曲線を描き始めました。
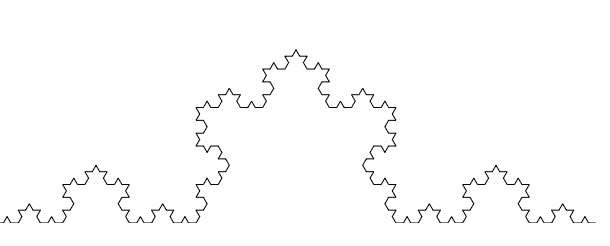
でも、まだ完成していません。

ここまではできました。

かなり試行錯誤をした結果となります。

線がX軸、Y軸に対して垂直水平にあるうちはよかったのですが、斜めになり座標系が回転すると、どうしたらいいかがわかっていません。

座標の計算方法は、ベースになる直線の始点に対して、変化値を足したり引いたりするわけですが、直線の傾きによって、足すべきか引くべきかが変わるという点が正しく制御できていないように思います。

計算のベースは以下を参考にさせていただきました。

引き続き、わからんところは考えていきたいと思います。

以下はメモ

現時点でのコード（上記の正しくないコッホ曲線を描くやつ）

use crate::js_sys::Math::abs;
use wasm_bindgen::prelude::*;
use wasm_bindgen::JsCast;
use web_sys::*;

// This is like the `main` function, except for JavaScript.
#[wasm_bindgen(start)]
pub fn main_js() -> Result<(), JsValue> {
    console_error_panic_hook::set_once();

    // Your code goes here!
    console::log_1(&JsValue::from_str("Hello world!"));

    let window = web_sys::window().unwrap();
    let document = window.document().unwrap();
    let canvas = document
        .get_element_by_id("canvas")
        .unwrap()
        .dyn_into::<web_sys::HtmlCanvasElement>()
        .unwrap();

    let context = canvas
        .get_context("2d")
        .unwrap()
        .unwrap()
        .dyn_into::<web_sys::CanvasRenderingContext2d>()
        .unwrap();

    context.move_to(0.0, 600.0);
    context.begin_path();

    draw_line(&context, [(0.0, 600.0), (600.0, 600.0)], 4);

    context.stroke();

    Ok(())
}

fn draw_line(context: &web_sys::CanvasRenderingContext2d, points: [(f64, f64); 2], depth: u8) {
    let [a, b] = points;
    console::log_1(&JsValue::from(&format!(
        "first ({}, {}), ({}, {})",
        a.0, a.1, b.0, b.1
    )));

    // 
    // 各点の基本形はこんな感じです。
    //         new
    //        /   \
    //       /     \
    // a----s       t----b
    //
    let sx = a.0 + (b.0 - a.0) / 3.0;
    let sy = a.1 + (b.1 - a.1) / 3.0;

    let tx = a.0 + 2.0 * (b.0 - a.0) / 3.0;
    let ty = a.1 + 2.0 * (b.1 - a.1) / 3.0;

    let mut new_x = 0.0;
    let mut new_y = 0.0;

    // ↓ この計算方法を思い出すのにすら時間がかかり、
    // degreeとradianというものも最初は忘れていた
    // 360 degree = 2 * pi radian
    // 360 degree = 2 * pi radian
    let theta = 2.0 * std::f64::consts::PI * 60.0 / 360.0; // 60 degree

    // ここが、試行錯誤の結果、謎の処理をしている部分です
    // もっと数学的に考えれば、適切に書けるはずなので要勉強
    if (ty - sy) >= 0.0 && (tx - sx) >= 0.0 {
        new_x = tx - (abs(tx - sx) * f64::cos(theta) - abs(ty - sy) * f64::sin(theta));
        new_y = ty - (abs(tx - sx) * f64::sin(theta) + abs(ty - sy) * f64::cos(theta));
    } else if (ty - sy) >= 0.0 && (tx - sx) < 0.0 {
        new_x = sx - (abs(tx - sx) * f64::cos(theta) - abs(ty - sy) * f64::sin(theta));
        new_y = sy + (abs(tx - sx) * f64::sin(theta) + abs(ty - sy) * f64::cos(theta));
    } else if (ty - sy) < 0.0 && (tx - sx) >= 0.0 {
        new_x = sx + (abs(tx - sx) * f64::cos(theta) - abs(ty - sy) * f64::sin(theta));
        new_y = sy - (abs(tx - sx) * f64::sin(theta) + abs(ty - sy) * f64::cos(theta));
    } else {
        new_x = tx + (abs(tx - sx) * f64::cos(theta) - abs(ty - sy) * f64::sin(theta));
        new_y = ty + (abs(tx - sx) * f64::sin(theta) + abs(ty - sy) * f64::cos(theta));
    }

    context.line_to(a.0, a.1);

    if depth - 1 > 0 {
        console::log_1(&JsValue::from(&format!(
            "({}, {}), ({}, {})",
            a.0, a.1, sx, sy
        )));
        draw_line(&context, [a, (sx, sy)], depth - 1);
    }

    context.line_to(sx, sy);

    if depth - 1 > 0 {
        console::log_1(&JsValue::from(&format!(
            "({}, {}), ({}, {})",
            sx, sy, new_x, new_y
        )));

        draw_line(&context, [(sx, sy), (new_x, new_y)], depth - 1);
    }
    context.line_to(new_x, new_y);

    if depth - 1 > 0 {
        console::log_1(&JsValue::from(&format!(
            "({}, {}), ({}, {})",
            new_x, new_y, tx, ty
        )));
        draw_line(&context, [(new_x, new_y), (tx, ty)], depth - 1);
    }

    context.line_to(tx, ty);

    if depth - 1 > 0 {
        console::log_1(&JsValue::from(&format!(
            "({}, {}), ({}, {})",
            tx, ty, b.0, b.1
        )));
        draw_line(&context, [(tx, ty), b], depth - 1);
    }
    context.line_to(b.0, b.1);
}

多分、キーワードは「座標の回転」とかです。