import numpy as np
%matplotlib inline
import matplotlib.pyplot as plt
import xarray as xr
xarray の応用
xarray の少し進んだ使い方を紹介します。
xarray については、以前の投稿 をご覧ください。
Rolling
pandas.rollingに対応するものです。
多次元データあるの軸に沿った小区間に対して、同じ操作を繰り返し行うことができます。
特に、その小区間を1点ずつずらしながら操作を適用し、同じサイズのデータを返します。
データを重複しない小区間に区切って、その中で代表値を決める操作は、
この次に説明する binning です。
例データ
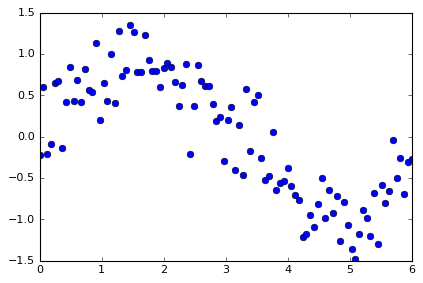
da = xr.DataArray(np.sin(np.linspace(0,6,100)) + np.random.randn(100)*0.3,
dims={'time'}, coords={'time':np.linspace(0,6,100)})
da
<xarray.DataArray (time: 100)>
array([-0.217099, 0.594632, -0.213687, -0.088451, 0.643075, 0.672311,
-0.133941, 0.419469, 0.836265, 0.436087, 0.688019, 0.416498,
0.81197 , 0.567076, 0.536079, 1.135186, 0.202363, 0.643781,
0.427754, 0.998932, 0.411504, 1.270951, 0.726597, 0.802427,
1.354037, 1.265239, 0.782349, 0.78666 , 1.231765, 0.931645,
0.793739, 0.797864, 0.59434 , 0.830584, 0.888593, 0.835981,
0.662846, 0.372863, 0.629388, 0.875347, -0.206508, 0.374656,
0.864203, 0.673541, 0.611431, 0.610227, 0.398388, 0.182321,
0.238973, -0.300663, 0.202904, 0.36229 , -0.399834, 0.134846,
-0.46481 , 0.578797, -0.177458, 0.416176, 0.502337, -0.262874,
-0.531168, -0.476578, 0.049585, -0.648642, -0.557033, -0.537415,
-0.38051 , -0.600608, -0.709828, -0.767893, -1.211113, -1.175812,
-0.948098, -1.091834, -0.814726, -0.499395, -0.98674 , -0.651322,
-0.922065, -0.713906, -1.268239, -0.787697, -1.071392, -1.356153,
-1.481535, -1.178269, -0.891799, -0.985956, -1.200543, -0.680796,
-1.305116, -0.588287, -0.804333, -0.662258, -0.036607, -0.501065,
-0.259611, -0.695071, -0.312524, -0.277099])
Coordinates:
* time (time) float64 0.0 0.06061 0.1212 0.1818 0.2424 0.303 0.3636 ...
plt.plot(da['time'], da, 'o')
[<matplotlib.lines.Line2D at 0x7f7a6f754048>]
rolling オブジェクトに対象とする軸と、移動平均のペアを指定します。
da_rolling = da.rolling(time=3).mean() # time軸に沿った方向に、3ポイントごとに移動平均をとる
da_rolling
<xarray.DataArray (time: 100)>
array([ nan, nan, 0.054615, 0.097498, 0.113646, 0.408978,
0.393815, 0.31928 , 0.373931, 0.56394 , 0.653457, 0.513534,
0.638829, 0.598515, 0.638375, 0.746113, 0.624543, 0.660443,
0.424633, 0.690156, 0.61273 , 0.893796, 0.803017, 0.933325,
0.96102 , 1.140568, 1.133875, 0.944749, 0.933591, 0.983356,
0.985716, 0.841082, 0.728648, 0.740929, 0.771172, 0.851719,
0.795807, 0.623897, 0.555032, 0.625866, 0.432742, 0.347832,
0.344117, 0.637467, 0.716392, 0.631733, 0.540015, 0.396979,
0.273227, 0.04021 , 0.047071, 0.088177, 0.05512 , 0.032434,
-0.243266, 0.082945, -0.021157, 0.272505, 0.247018, 0.218546,
-0.097235, -0.42354 , -0.319387, -0.358545, -0.385363, -0.58103 ,
-0.491653, -0.506178, -0.563649, -0.692776, -0.896278, -1.051606,
-1.111675, -1.071915, -0.951553, -0.801985, -0.766954, -0.712486,
-0.853376, -0.762431, -0.96807 , -0.92328 , -1.042442, -1.071747,
-1.303026, -1.338652, -1.183868, -1.018675, -1.0261 , -0.955765,
-1.062152, -0.858066, -0.899245, -0.684959, -0.501066, -0.399977,
-0.265761, -0.485249, -0.422402, -0.428231])
Coordinates:
* time (time) float64 0.0 0.06061 0.1212 0.1818 0.2424 0.303 0.3636 ...
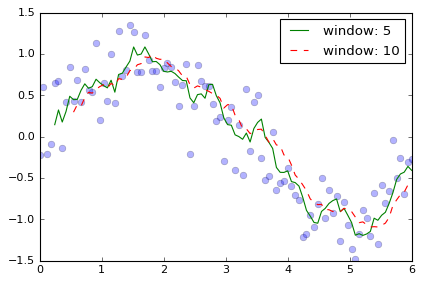
plt.plot(da['time'], da, 'o', alpha=0.3)
plt.plot(da['time'], da.rolling(time=5).mean(), '-', label='window: 5')
plt.plot(da['time'], da.rolling(time=10).mean(), '--', label='window: 10')
plt.legend()
<matplotlib.legend.Legend at 0x7f7a7180c908>
引数
pandasと同じように、rollingメソッドにより、Rollingクラスが返されます。
da.rolling(time=3)
DataArrayRolling [window->3,center->False,dim->time]
rollingオブジェクトを作るための引数は
- windows (辞書型)
上記のように、軸名をキーに、移動平均の点数を要素にして渡します。
(なお、現在は単一の軸に対するrollingにのみ対応しています。)
の他に、
- min_periods (整数, default : None)
min_periodsを指定すると、それ以下の点数しかない区間の値はnanになります。 - center (論理値, default : False)
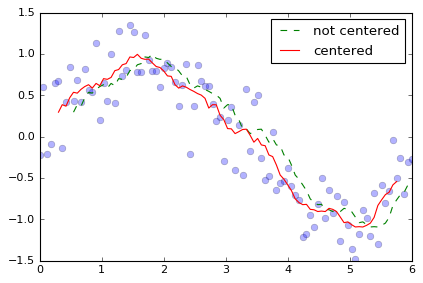
center を True にすると、計算値が窓の中心に入ります。
plt.plot(da['time'], da, 'o', alpha=0.3)
plt.plot(da['time'], da.rolling(time=10).mean(), '--', label='not centered')
plt.plot(da['time'], da.rolling(center=True, time=10).mean(), '-', label='centered')
plt.legend()
<matplotlib.legend.Legend at 0x7f7a6f69fb70>
メソッド
'argmax', 'argmin', 'max', 'min', 'mean', 'prod', 'sum', 'std', 'var', 'median' などの numpyメソッドに対応しています。
さらに。reduce(func, **kwargs) メソッドも用意されています。
例えば
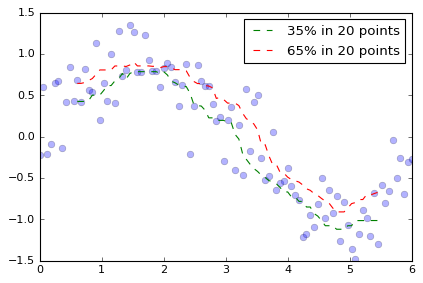
da_35percent = da.rolling(time=20, center=True).reduce(np.percentile, q=35)
da_65percent = da.rolling(time=20, center=True).reduce(np.percentile, q=65)
plt.plot(da['time'], da, 'o', alpha=0.3)
plt.plot(da['time'], da_35percent, '--', label='35% in 20 points')
plt.plot(da['time'], da_65percent, '--', label='65% in 20 points')
plt.legend()
<matplotlib.legend.Legend at 0x7f7a6f7a5a20>
のように、任意の関数オブジェクトを渡すことができます。
ただし、渡す関数オブジェクトは上記 numpy メソッドのように、
どの軸をreduceするか指定するaxisに対応している必要があります。
応用 ~数値的コンボリューション~
簡単な応用としては、コンボリューションが挙げられます。
$$
[f * g]i = \sum{n}^{N} f_{i-n} g_n
$$
ここで、$f_i$ はコンボリューションされるデータ
$g_n$ はサイズ $N$ のコンボリューションするデータです。
以下では、ウェーブレット的な関数を畳み込んでみます。
# functor to apply convolution
def conv(src, obj, axis=0):
"""
+ src: target data to be convoluted
+ obj: convoluting data
+ axis: which axis of src to convolute
"""
if src.shape[axis] == obj.shape[0]:
return np.sum(src*obj, axis=axis)
else:
return 0.0
# convoluting data
n_window = 20
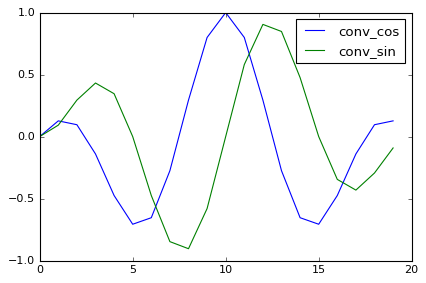
conv_cos = np.cos(2.0*np.pi * 2.0 * np.arange(n_window) / n_window) * np.sin(np.pi * np.arange(n_window) / n_window)
conv_sin = np.sin(2.0*np.pi * 2.0 * np.arange(n_window) / n_window) * np.sin(np.pi * np.arange(n_window) / n_window)
plt.plot(conv_cos, label='conv_cos')
plt.plot(conv_sin, label='conv_sin')
plt.legend(loc='best')
<matplotlib.legend.Legend at 0x7f7a6f585b00>
da_cos = da.rolling(time=20, center=True).reduce(conv, obj=conv_cos)
da_sin = da.rolling(time=20, center=True).reduce(conv, obj=conv_sin)
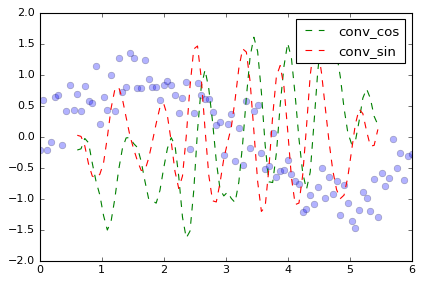
plt.plot(da['time'], da, 'o', alpha=0.3)
plt.plot(da['time'], da_cos, '--', label='conv_cos')
plt.plot(da['time'], da_sin, '--', label='conv_sin')
plt.legend()
<matplotlib.legend.Legend at 0x7f7a6f5c1978>
Dataset.rolling
複数の xr.DataArray を集めた xr.Dataset も rolling に対応しています。
ds = xr.Dataset({'sin': ('time', np.sin(np.linspace(0,6,100)) + np.random.randn(100)*0.3),
'cos': ('time', np.cos(np.linspace(0,6,100)) + np.random.randn(100)*0.3)},
coords={'time':np.linspace(0,6,100)})
ds
<xarray.Dataset>
Dimensions: (time: 100)
Coordinates:
* time (time) float64 0.0 0.06061 0.1212 0.1818 0.2424 0.303 0.3636 ...
Data variables:
sin (time) float64 0.5826 -0.04678 -0.1069 -0.05271 0.08796 0.1871 ...
cos (time) float64 0.7281 0.9172 1.015 0.9138 0.4236 0.8481 0.8641 ...
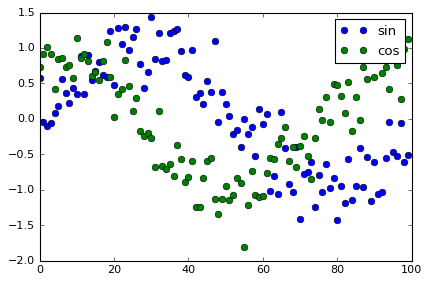
plt.plot(ds['sin'], 'o', label='sin')
plt.plot(ds['cos'], 'o', label='cos')
plt.legend()
<matplotlib.legend.Legend at 0x7f7a6f4a6518>
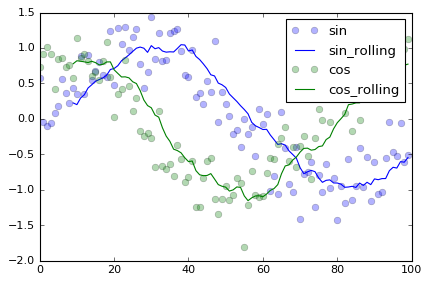
ds_mean = ds.rolling(time=10).mean()
plt.plot(ds['sin'], 'bo', label='sin', alpha=0.3)
plt.plot(ds_mean['sin'], '-b', label='sin_rolling')
plt.plot(ds['cos'], 'go', label='cos', alpha=0.3)
plt.plot(ds_mean['cos'], '-g', label='cos_rolling')
plt.legend()
<matplotlib.legend.Legend at 0x7f7a6f4b9080>
binning
rolling に似た機能として binning が挙げられます。
これは group_bins 操作で実現できます。
pandas.groupby_binsに対応するものです。
多次元データあるの軸に沿った重複しない小区間に対して、同じ操作を繰り返し行うことができます。
上記のdaの時間方向に10等分してその中の平均値を求めるには、
group引数に軸のラベルを、bins引数に等分の数を渡します。
最後にmeanメソッドを実行することで、新しいxr.DataArrayが作られます。
da_bin_mean = da.groupby_bins(group='time', bins=10).mean()
da_bin_mean
<xarray.DataArray (time_bins: 10)>
array([ 0.294866, 0.642766, 0.956317, 0.728154, 0.344657, 0.089237,
-0.516009, -0.901501, -1.090238, -0.544197])
Coordinates:
* time_bins (time_bins) object '(-0.006, 0.6]' '(0.6, 1.2]' '(1.2, 1.8]' ...
新しく作られた DataArray は、中身が平均値、軸が少区間の両端の値に相当する点が格納されています。
実際の用途では、指定した小区間に対する操作がしたいことがあります。
その場合は、小区間の区切り点をbins引数に与えます。さらに、
bins = np.linspace(0,6,11) # 10個に区切る場合、両端を含めた小区間の区切り点である11個のアレイを渡す。
bin_labels = bins[:-1] + 0.3 # 10点に対応する軸を用意する。
da_bin_mean = da.groupby_bins(group='time', bins=bins, labels=bin_labels).mean()
da_bin_mean
<xarray.DataArray (time_bins: 10)>
array([ 0.351751, 0.642766, 0.956317, 0.728154, 0.344657, 0.089237,
-0.516009, -0.901501, -1.090238, -0.544197])
Coordinates:
* time_bins (time_bins) float64 0.3 0.9 1.5 2.1 2.7 3.3 3.9 4.5 5.1 5.7
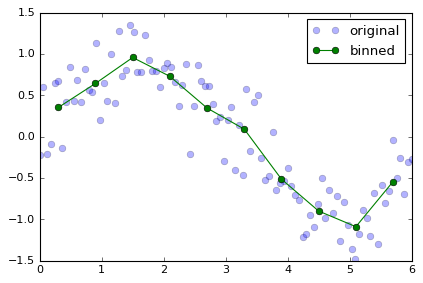
plt.plot(da['time'], da, 'o', label='original', alpha=0.3)
plt.plot(da_bin_mean['time_bins'], da_bin_mean, '-o', label='binned')
plt.legend()
<matplotlib.legend.Legend at 0x7f7a6f5a9748>