この記事は古川研究室 Workout_calendar 19日目の記事です。
本記事は古川研究室の学生が学習の一環として書いたものです。内容が曖昧であったり表現が多少異なったりする場合があります。
はじめに
機械学習について学んでいると、代表的なタスクのひとつ、クラス分類のところで線形分離可能という言葉が出てきました。どういうものか気になったので、イメージを掴むために例を挙げながら考えていきます。具体的には、論理回路のひとつであるAND回路(プログラミングで言うAND演算を行う素子)を例に、その出力を線形分離可能かどうか、図と数式で見ていきます。最後に簡単にプログラムの実装をして確認も行います。
定義
2つのカテゴリーに属するパターンの集合が、ある超平面によって2つのカテゴリそれぞれに分離されるとき、このパターン集合は線形分離可能であるという。[1]
超平面:n次元空間内にある(n-1)次元空間 1次元では点、2次元では直線、3次元では平面になる
分離:2つの集合が交わりを持たない 2次元の散布図をイメージするとわかりやすい
AND回路の出力の線形分離
入力と出力の関係がわかりやすいものとして、電子回路に用いられる論理回路があります。プログラミングにおいても論理演算子というものがあって同様の働きをするので、馴染みやすいのではないのでしょうか。
ここでは論理回路のひとつであるAND回路を例に、その出力が線形分離可能かどうか、図と式で見ていきましょう。
線形分離可能か図で確かめる
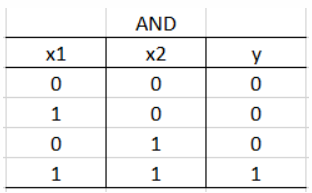
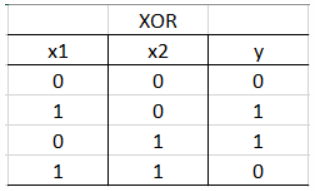
AND回路の出力は、次の真理値表のようになります。
真理値表:論理回路の入力と出力の関係を一覧するための図
- AND回路の真理値表
$x1$、$x2$ が入力、$y$ が出力になります。真理値表を見るとわかるように、AND回路では入力が両方とも"1"のときのみ出力が"1"になります。それ以外では出力は"0"になります。今回はこの出力を線形分離によって、"0" と "1" の2クラスにわけられるか確かめます。
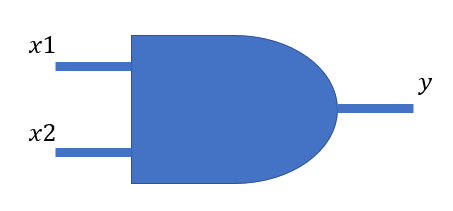
ちなみに、AND回路素子を図記号で表すと次のようになります。
- AND回路素子の図記号
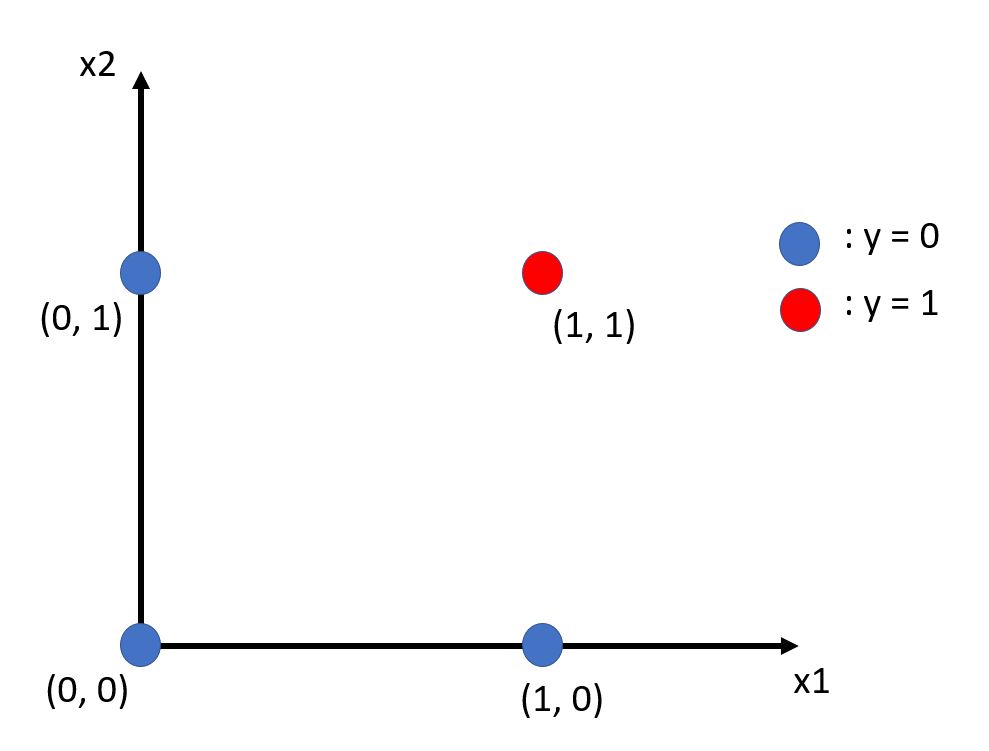
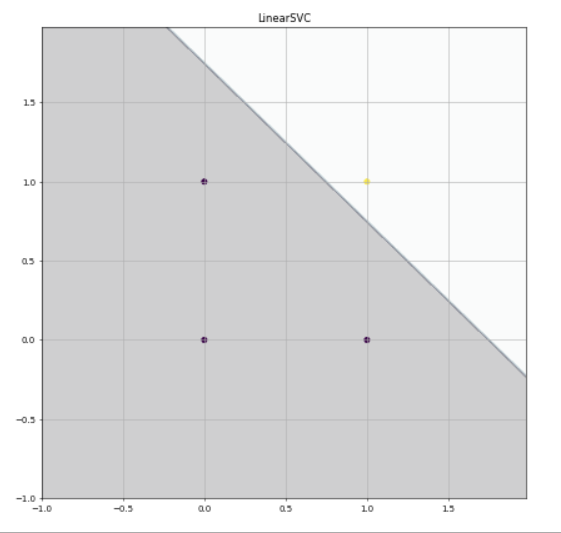
それでは、線形分離可能か調べるために、真理値表の入力と出力の関係を2次元の図にプロットしてみましょう。
- 2次元の図にプロットしたAND回路の出力
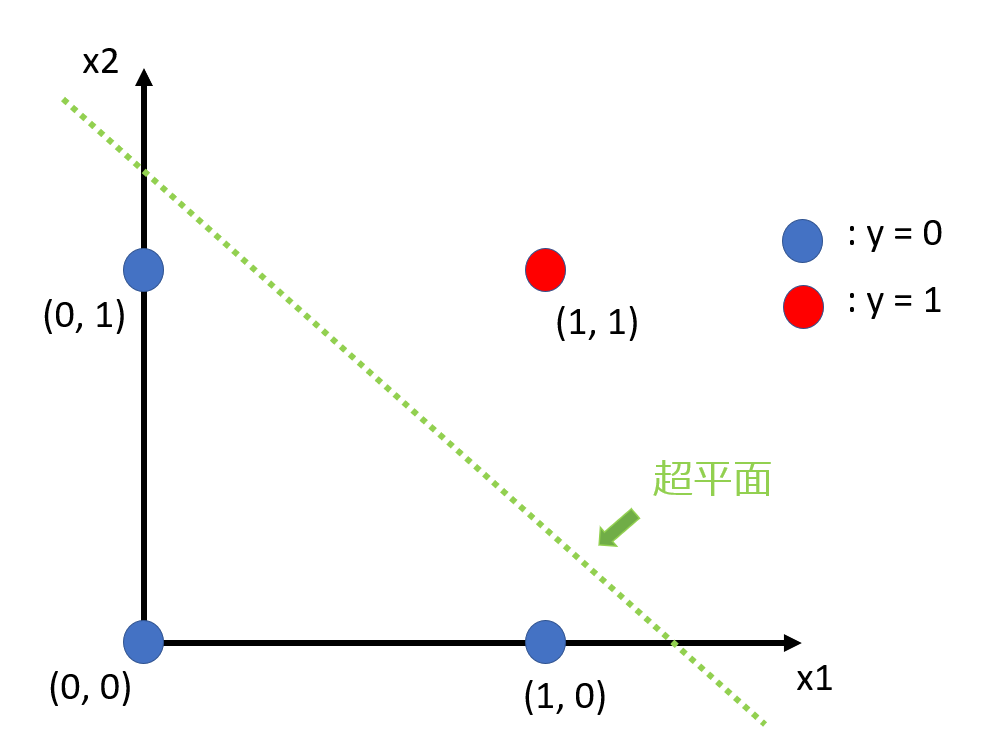
わかりやすくプロットできました。それではここに超平面を描きこんでみましょう。
- 超平面によるAND回路の出力の分離
どうやら超平面によって分離できたようです。こうなることで、線形分離可能であるということができます。
図に表すとこのようになるのですね!イメージは掴めましたでしょうか?
次は数式で確かめてみましょう。
線形分離可能か数式で確かめる
入力の集合を2つに分けて
$X^+$: $y = 1$の集合
$X^-$: $y = 0$の集合
とします。
ある入力 $x_s$($x_1,x_2$の組) に対して二次元の式を考えて
$\Phi(x) = w_0 + w_1 x_1 + w_2 x_2$
とします。このとき、
$y = 1$ にする入力が来た時に $\Phi(x_s) > 0$
$y = 0$にする入力が来た時に $\Phi(x_s) < 0$
となるように式 $\Phi(x)$ の係数 $w_0, w_1, w_2$ を求めて分離します。
ここで式 $\Phi(x)$ の各係数(パラメータ)を推定することが機械学習の分類において解くべき問題となりますが、ここでは線形分離可能かどうか確かめることが目的のため、
$w_0 = -1.5, w_1 = 1, w_2 = 1$
と定めることにします。
パラメータを式 $\Phi(x)$ に代入し、真理値表と比較して確かめてみましょう。
$(0,0)$ のとき $\Phi((0,0)) = -1.5 + 1 * 0 + 1 * 0 = -1.5 < 0$
$(1,0)$ のとき $\Phi((1,0)) = -1.5 + 1 * 1 + 1 * 0 = -0.5 < 0$
$(0,1)$ のとき $\Phi((0,1)) = -1.5 + 1 * 0 + 1 * 1 = -0.5 < 0$
$(1,1)$ のとき $\Phi((1,1)) = -1.5 + 1 * 1 + 1 * 1 = 0.5 > 0$
入力 $x_1$、$x_2$ について、どちらとも"1"の場合は式 $\Phi(x)$ の値が"0"より大きくなり、それ以外では"0"より小さくなっています。よって出力 $y$ について分離できていると言えます。従って、AND回路の出力は線形分離可能であることが数式で確かめられました。
図と数式での説明のまとめ
以上、図と式で見て、AND回路の出力は線形分離可能なことがわかりました。すぐにはイメージが固まらずとも、特に超平面については知っておくと良いと思います。数式も、図と関連付けすることでイメージを補完すると理解に繋がります。
さて、ここまで図と式を見るだけでしたが、機械学習のタスクということでもちろんプログラムで実装することもできます。最後にプログラミングで手を動かして線形分離ができることを確かめて、仕上げとしましょう。
AND回路の出力の線形分離を実装してみる
Python で線形SVMといわれる線形分離を行う手法を実装して、AND回路の出力が線形分離されることを確かめてみましょう。
ソースコード
from sklearn.datasets import make_blobs
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
import numpy as np
import matplotlib.pyplot as plt
# 説明変数
X = np.array([[1, 1],[1, 0],[0, 1],[0, 0]])
print(X)
# 目的変数
Y = np.array([1,0,0,0])
print(Y)
# 線形サポートベクタマシン
# 訓練データ、テストデータ(今回は同じ)
X_train=X
X_test=X
y_train=Y
y_test=Y
fig = plt.figure(figsize=(10,10),dpi=50)
# 訓練データ散布図プロット
plt.scatter(X_train[:, 0], X_train[:, 1], c=y_train.T)
# テストデータ散布図プロット
plt.scatter(X_test[:, 0], X_test[:, 1], c=y_test.T, marker='*')
# 線形サポートベクタマシン学習
clf = LinearSVC().fit(X,Y)
# データの範囲でメッシュ状に点を取る
training_x_min = X[:, 0].min() - 1
training_x_max = X[:, 0].max() + 1
training_y_min = X[:, 1].min() - 1
training_y_max = X[:, 1].max() + 1
grid_interval = 0.02
xx, yy = np.meshgrid(
np.arange(training_x_min, training_x_max, grid_interval),
np.arange(training_y_min, training_y_max, grid_interval),
)
# 各点を分類する
Z = clf.predict(np.c_[xx.ravel(), yy.ravel()])
# 分類結果を表示する
Z = Z.reshape(xx.shape)
plt.contourf(xx, yy, Z, cmap=plt.cm.bone, alpha=0.2)
# グラフを表示する
plt.autoscale()
plt.grid()
plt.title("LinearSVC")
plt.show()
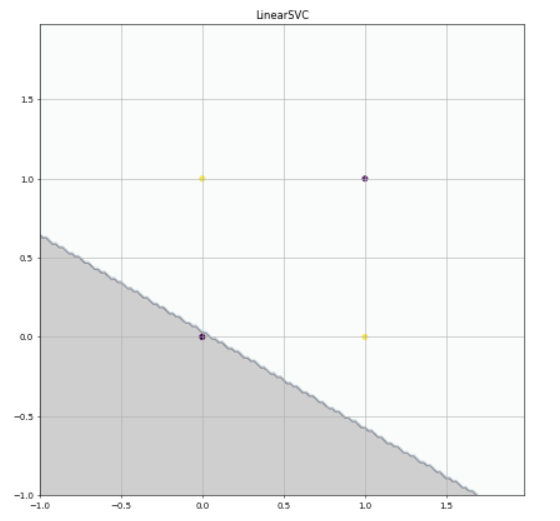
- 実行結果
黄色の点が出力 $1$ のとき、
黒の点が出力 $0$ のときになります。
きれいに線形分離できました。ぜひお手元で動かして確かめてみてください。
おわりに
筆者自身、イメージを掴めないと理解が先へ進まないので、参考ページにて電子回路の例を挙げて解説されているのを見かけたことをきっかけにこのような記事を作成してみましたが、いかがでしたでしょうか。線形分離のイメージを掴む助けとなれば幸いです。
これに限りませんが、人は脳内に自分なりの"イメージ"(図に限らない)を持てないと物事を理解できないと言われます。理解が行き詰ったときは、自分にとってわかりやすい例を探してみると良いのかなと思います。今回、私にとってはそれが電子回路でした。
おまけ:線形分離できない論理回路の例
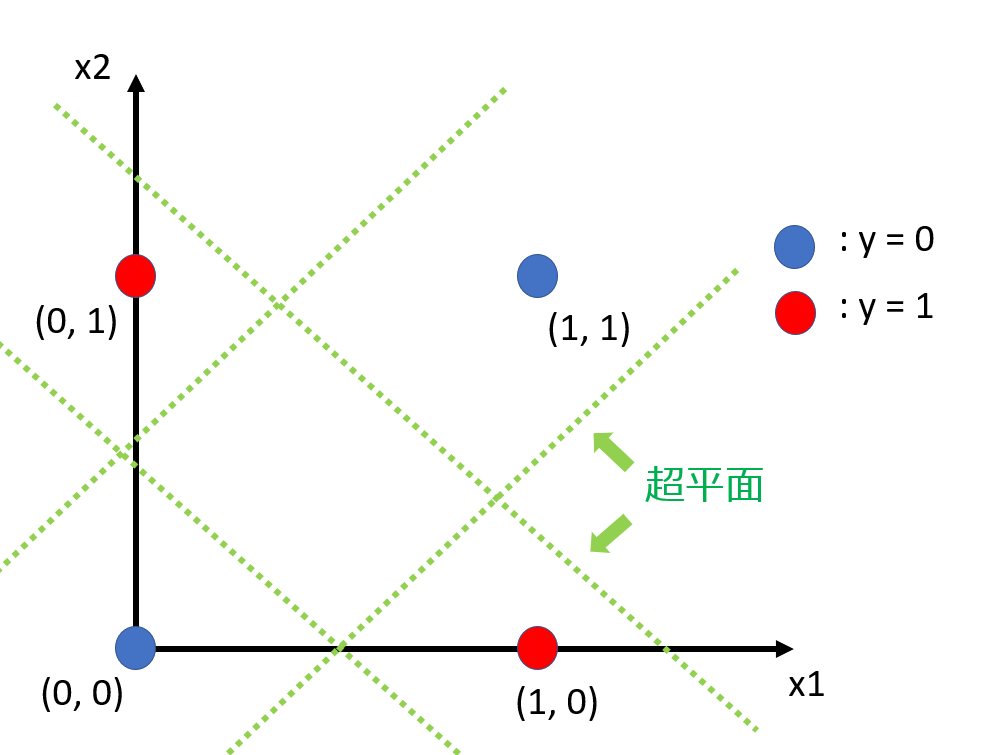
今回は線形分離可能なAND回路を扱いましたが、線形分離不可能なものもあります。論理回路の例で言えば、XOR回路の出力は線形分離できません。XOR回路は入力が同じ値でないとき、つまりどちらかが"1"でもう一方が"0"のときのみ出力が"1"になる論理回路です。
図からわかるように、超平面では2つのクラスに分類できず、線形分離不可能です。AND回路の場合と同様に線形SVMを試して確かめてみると
- 実行結果
このように分離することができません。こちらも先ほどのプログラムの変数を少し変更すると実行できるので試してみてください。
XOR回路のような線形分離不可能な例を非線形問題といいます。線形SVMは線形問題しか解くことができないため、XOR回路の出力を分離することはできませんでした。このような非線形問題を解く手法は別にありますが、筆者もまだまだ勉強中のためまたの機会ということで!
参考ページ
線形分離可能 ー 単純パーセプトロンの限界
https://screwandsilver.com/linearly_separable_of_perceptrons/ [1]
線形分離と多層パーセプトロン
https://www.infiniteloop.co.jp/blog/2017/12/learning-keras-03/ [2]
線形モデルによるクラス分類
https://aithii.com/2018/11/18/post-450/ [3]
識別関数の前知識
http://hokuts.com/2015/11/24/ml1_func/ [4]