この記事は DeNA 21 新卒 Advent Calendar 2020 の21日目の記事です.
目次
はじめに
最近 ML (Machine Learning) について学ぶ機会があったので,基礎的なアルゴリズムをまとめます.
この記事では,**教師あり学習(最小二乗法,正則化,ロジスティック回帰,ナイーブベイズ学習)**について説明します.
各アルゴリズムの原理を主に説明し,その後にscikit-learnを用いて実際に学習させます.
最小二乗法
まず線形回帰1を実現する最小二乗法(least squares method)について説明します.
原理
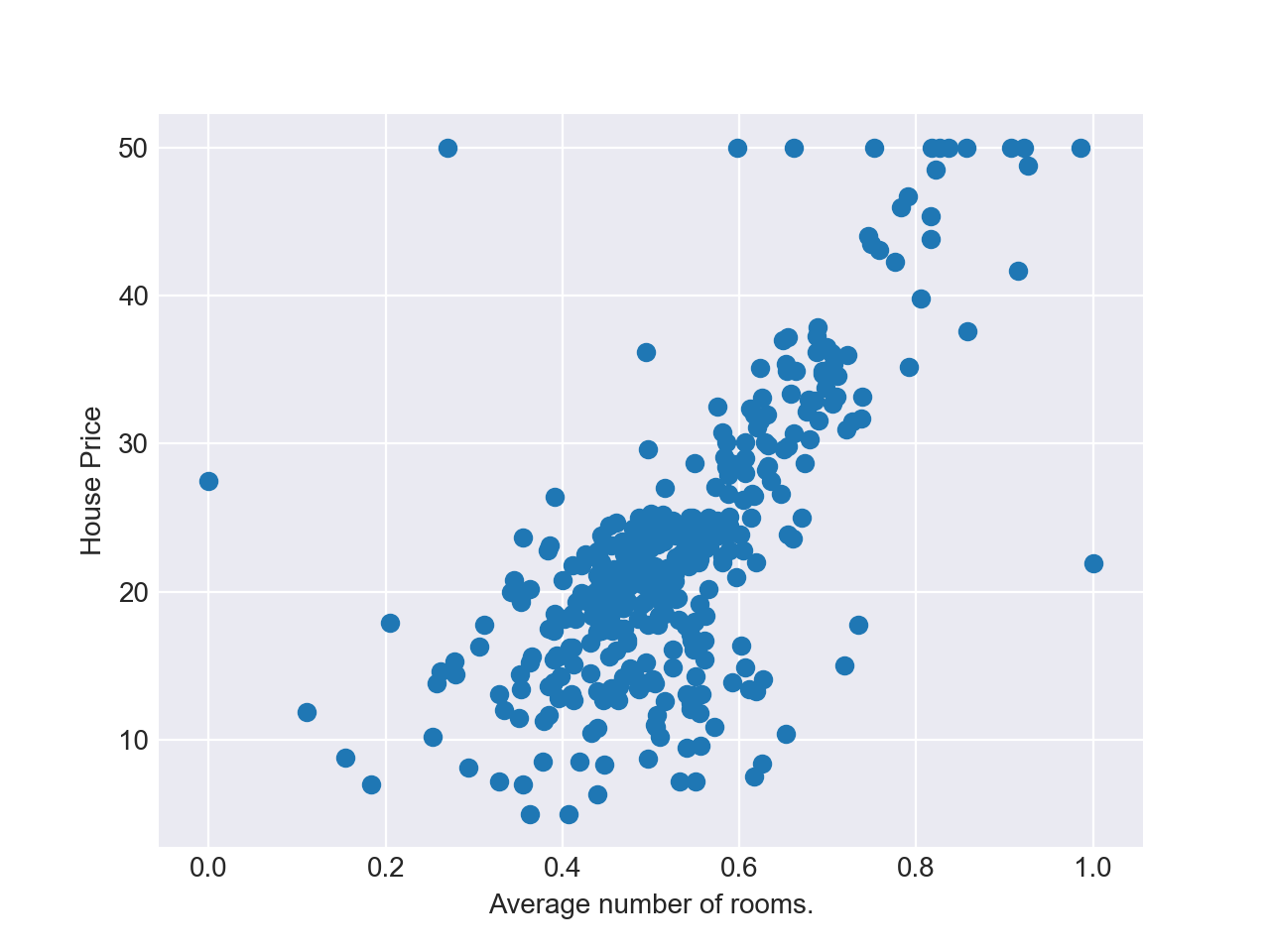
まず以下のグラフをご覧ください.
このグラフは,ボストンの住居の平均部屋数(Average number of rooms)と,対応する住宅価格(House Price)の関係を表したものです2.
このデータを元に,未知の住居の平均部屋数が入力された場合に,最適な住宅価格を予測することを考えます.
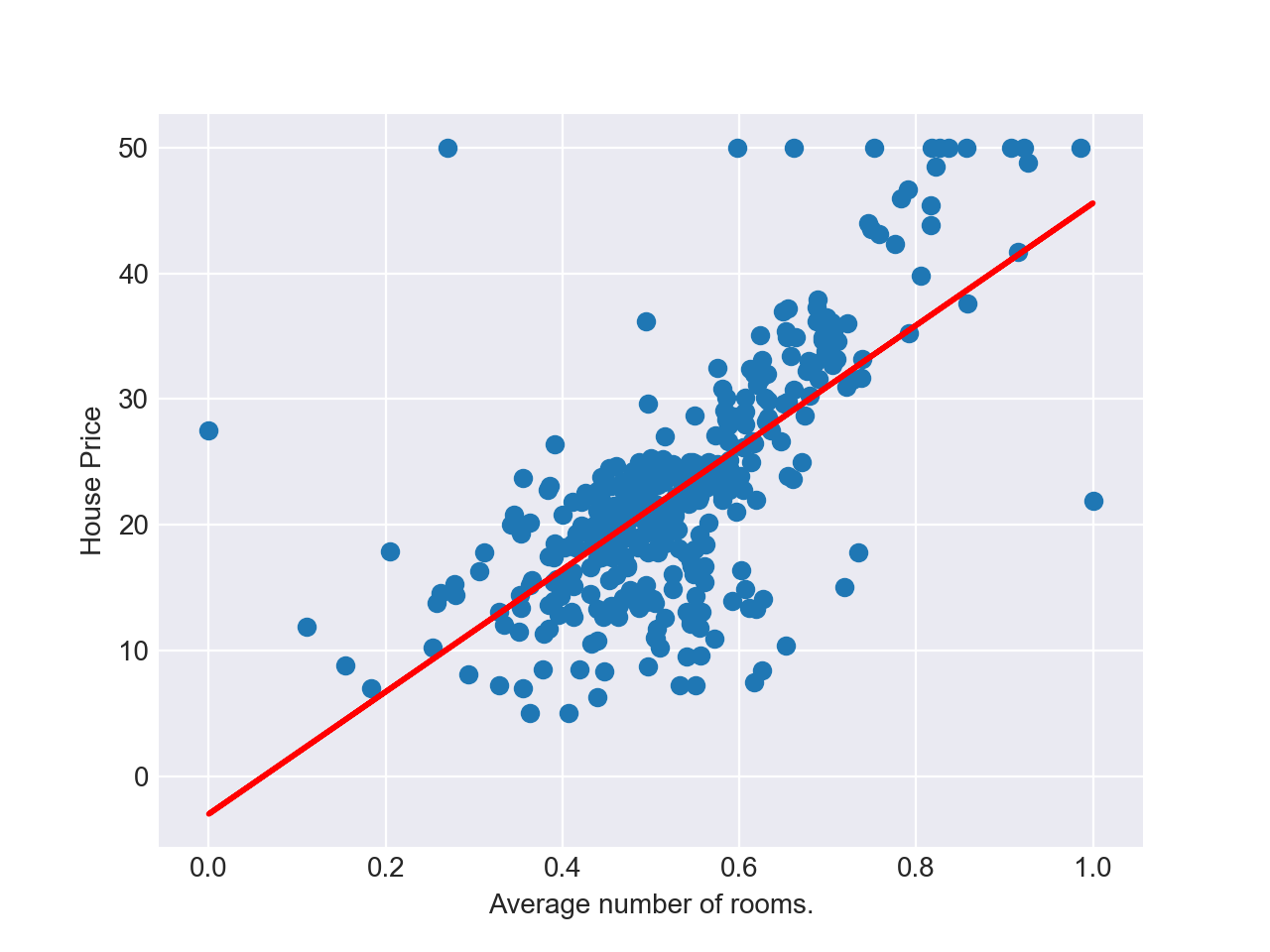
最小二乗法では,このグラフに対して以下のような「最適な」直線 $y = f(x)$ を引くことによって,未知の入力$x$に対する予測値 $f(x)$ を計算します.
では,どういう直線が「最適な」直線なのかというと,最小二乗法という名前の通り,データとモデルの予測値の誤差の二乗和が最小となる直線が最適だと考えます.
つまり,データ$(x_i, y_i)$に対して $(i = 1, ..., n)$,以下の値 $E$ が最小となるような直線 $y=w_0+w_1x$ が最適だと考えます3.
$$ E = \frac{1}{2} \sum_{i=1}^n(y_i - (w_0 + w_1x_i))^2 $$
あとは $E$ を最小にする重みパラメータ $w_0, w_1$を見つければ良いことになりますが,この説明をすると長くなってしまうので,本記事では割愛します4.この辺は詳しく知らなくても,MLライブラリがよしなにやってくれます.
ここまでは,入力変数が「住居の平均部屋数」のみの場合を考えてきました.1つの入力変数のみを用いた線形回帰モデルのことを「単回帰モデル」と呼びます.
実は,入力変数が複数の場合でも線形回帰モデルを構築することができます.この場合の線形回帰モデルのことを「重回帰モデル」と呼びます.重回帰モデルの場合,上のグラフのような直線を求めるのではなく,平面を求めることになります.
実装
ここからはscikit-learnを用いて学習させます.
以下でサンプルを実行するために,mglearnをインストールしましょう.mglearnをインストールすることによって,scikit-learnを含む複数のライブラリがインストールされます.
$ pip install mglearn
scikit-learnを用いると,最小二乗法を用いた線形回帰モデルを簡単に実装することができます.
以下にコードを示します.scikit-learnの使い方を知らなくてもなるべく理解できるようにコメントしてあります.
やっていることとしては,
- 訓練データとテストデータを分割し,
-
LinearRegressionメソッドを利用して最小二乗法を適用し, - 構築した単回帰モデルで訓練データを予測する
ということをやっています.
import matplotlib.pyplot as plt # グラフ化するために必要なライブラリ
from mglearn.datasets import load_extended_boston # 利用するデータセット
from sklearn import linear_model # 線形回帰を実現するためのメソッド (最小二乗法)
from sklearn.model_selection import train_test_split # 訓練データとテストデータに分割するメソッドである train_test_split
x_data, y_data = load_extended_boston()
# 訓練データとテストデータに分割する
# x_data_train: 住居の平均部屋数を含む訓練データセット
# x_data_test: 住居の平均部屋数を含むテストデータセット
# y_data_train: 対応する住宅価格に関する訓練データセット
# y_data_test: 対応する住宅価格に関するテストデータセット
x_data_train, x_data_test, y_data_train, y_data_test = train_test_split(x_data, y_data, random_state=0)
# 住居の平均部屋数を取得する
# 上が訓練用,下がテスト用(後にモデルを評価する際に使う)
avg_rooms_train = x_data_train[:, 5].reshape(-1, 1)
avg_rooms_test = x_data_test[:, 5].reshape(-1, 1)
# 線形単回帰モデルを適用する
l_model = linear_model.LinearRegression()
l_model.fit(avg_rooms_train, y_data_train) # 訓練データを元に、直線y=f(x)を求める
# 上記で作成したモデルを使って,対応する住宅価格を予測する
y_pred_train = l_model.predict(avg_rooms_train)
# グラフ化する
plt.xlabel('Average number of rooms.') # 横軸のラベルを貼る
plt.ylabel('House Price') # 縦軸のラベルを貼る
plt.plot(avg_rooms_train, y_pred_train, color='red') # 予測直線を出力
plt.scatter(avg_rooms_train, y_data_train) # 訓練データの散布図を出力
plt.show() # グラフ出力
これを実行すると,先ほどのようなグラフが得られます.
直線の切片と傾きを計算したい場合は,以下を付け足します.
...
itc = l_model.intercept_ # 切片を導出する
print("切片: {0}".format(itc))
coef = l_model.coef_[0] # 傾きを導出する
print("傾き: {0}".format(coef))
付け足して実行すると,以下の出力が得られます.
切片: -3.017580453873432
傾き: 48.60428200855903
最後に,この単回帰モデルの性能を評価します.
線形回帰モデルの評価には,$R^2$ スコアというものを用います.以下の式で表されます.
$$ R^2 = 1 - \frac{\sum_{i=1}^n(y_i - \hat{y_i})^2}{\sum_{i=1}^n(y_i - \mu)^2} $$
ただし,$\hat{y_i}$はモデルの予測値($\hat{y_i}=w_0+w_1x_1+w_2x_2+...+w_nx_n$),$\mu$は訓練データの平均値($\mu = (\sum_{i=1}^n y_i) / {n}$)を表します.
$R^2$スコアは0から1までの値をとり,1に近づくほど性能が良いです.
scikit-learnで$R^2$スコアを計算するには,以下のコードを記述します.
...
# モデルを評価する
train_data_score = l_model.score(avg_rooms_train, y_data_train)
test_data_score = l_model.score(avg_rooms_test, y_data_test)
print("R^2 score (train case) = {0}".format(train_data_score))
print("R^2 score (test case) = {0}".format(test_data_score))
実行すると,以下の出力を得ます.
R^2 score (train case) = 0.4875206793934366
R^2 score (test case) = 0.4679000543136782
訓練データでのスコアも,テストデータでのスコアもイマイチなので,
上記で行った単回帰モデルの性能はあまり良いとは言えない結果になりました.
重回帰モデルも同様に評価することができます.
単回帰モデルの一部分を以下のように書き換えましょう.
...
- # 線形単回帰モデルを適用する
- l_model = linear_model.LinearRegression()
- l_model.fit(avg_rooms_train, y_data_train) # 訓練データを元に、直線y=f(x)を求める
+ # 線形重回帰モデルを適用する
+ l_model = linear_model.LinearRegression()
+ l_model.fit(x_data_train, y_data_train)
# モデルを評価する
train_data_score = l_model.score(x_data_train, y_data_train)
test_data_score = l_model.score(x_data_test, y_data_test)
print("R^2 score (train case) = {0}".format(train_data_score))
print("R^2 score (test case) = {0}".format(test_data_score))
すると以下のような結果が得られます.
R^2 score (train case) = 0.9520519609032727
R^2 score (test case) = 0.6074721959665571
単回帰モデルに比べて,スコアが少し高くなっています.
一方で,訓練データに対するスコアは0.952と非常にいい結果が出ているにもかかわらず,テストデータに対するスコアは0.607とあまりいい結果になっていないことが確認できます.
このように,モデルが訓練データに過剰に適応し,テストデータに対してはスコアが低くなる現象を過学習といいます.
この過学習を防ぐための工夫として,正則化 というものがあります.
次はこの正則化について説明します.
L1正則化とL2正則化
ここでは,線形回帰モデルで発生する過学習を抑えるための手法である正則化について説明します.
原理
L1正則化(Lassoともいう)とL2正則化(Ridge回帰ともいう)は,ともに重みパラメータに制約をかけて,過学習を抑制する効果を持ちます.
具体的には,L1正則化においては,以下の$E$が最小となるような重みパラメータを計算します.
$$ E = \frac{1}{2} \sum_{i=1}^n(y_i - \hat{y_i})^2 + \alpha ||w||_1 $$
ただし,$||w||_1=|w_0|+|w_1|+...+|w_n| $ とします.
L2正則化においては,以下の$E$が最小となるような重みパラメータを計算します.
$$ E = \frac{1}{2} \sum_{i=1}^n(y_i - \hat{y_i})^2 + \alpha ||w||_2 $$
ただし,$||w||_2 = w_0^2+w_1^2+...+w_n^2 $ とします.
また$\alpha$は正規化の強さを調整するパラメータで,0から1までの値をとります.
両方に共通していることは,最小二乗法で使用した$E$の式に,$\alpha||w||_k$という項が追加されていることです.
なぜこのような項を追加するのか簡単に説明します.
ナイーブな最小二乗法を用いて学習すると,重みパラメータの一部が極端に大きくなったり,または小さくなったりする傾向があります.その結果,訓練データにのみ順応するような複雑なモデルが出来上がってしまいます.
それを防ぐためには,重みパラメータが小さすぎたり大きすぎたりした場合に,ペナルティを加えるようにすれば良いです.そのペナルティが $\alpha||w||_k$ に相当するわけです.
ここまで,過学習を抑える工夫について説明しました.
最後に,L1正則化とL2正則化を使い分けるポイントについて説明します.
一般的に,L1正則化は重みパラメータが0になりやすく,次元圧縮のために用いられます.一方,L2正則化は重みパラメータが完全に0になることはなく,全ての入力変数の値を考慮して学習したい場合に用いられます.
過学習を防ぐ際に,全ての入力変数を重要視したい場合はL2正規化,次元圧縮をしても良い場合はL1正規化を採用すると良いでしょう5.
実装
L1正則化とL2正則化の実装の流れは,基本的には最小二乗法の場合と同じです.
異なる部分として,LinearRegressionの代わりに,RidgeやLassoというメソッドを使います.
...
- l_model = linear_model.LinearRegression()
+ ridge_model = linear_model.Ridge(alpha=/* αを入力 */, random_state=0) # L2正則化
+ lasso_model = linear_model.Lasso(alpha=/* αを入力 */, max_iter=/* 最適解探索の際の最大探索回数を指定 */, random_state=0) # L1正則化
それぞれ学習させてみると,以下のような結果が得られました.
L1正則化については,例えばalpha=0.1の場合,以下の結果が得られました.
先ほどと比べて,過学習が抑えられていることが確認できます.
# L1正則化(alpha=0.1)
R^2 score (train case) = 0.9282273685001985
R^2 score (test case) = 0.7722067936480157
ちなみに,alphaの値を0から1まで0.01刻みでスコアを算出したところ,alphaが小さいほどスコアが高く,過学習が抑えられていることが確認できました.
# 結果の一例:
alpha = 0.0
R^2 score (train case) = 0.950703672946392
R^2 score (test case) = 0.6085007464864356
alpha = 0.01
R^2 score (train case) = 0.9444599240824938
R^2 score (test case) = 0.7022485939224441
alpha = 0.02
R^2 score (train case) = 0.940672234687759
R^2 score (test case) = 0.7330975588167472
alpha = 0.03
R^2 score (train case) = 0.9380926477091954
R^2 score (test case) = 0.7477903146587561
alpha = 0.04
R^2 score (train case) = 0.9360826368889351
R^2 score (test case) = 0.7562018013467819
alpha = 0.05
R^2 score (train case) = 0.9343998622870333
R^2 score (test case) = 0.7615599966002603
alpha = 0.06
R^2 score (train case) = 0.9329294684214201
R^2 score (test case) = 0.7652093121517151
.
.
.
alpha = 0.95
R^2 score (train case) = 0.8873240143272362
R^2 score (test case) = 0.7541730215613112
alpha = 0.96
R^2 score (train case) = 0.8870149090412837
R^2 score (test case) = 0.7538905098075779
alpha = 0.97
R^2 score (train case) = 0.8867076459073084
R^2 score (test case) = 0.7536087859077836
alpha = 0.98
R^2 score (train case) = 0.8864021995301943
R^2 score (test case) = 0.753327850681055
alpha = 0.99
R^2 score (train case) = 0.8860985451293656
R^2 score (test case) = 0.7530477046732349
ペナルティを大きくすることで,必ずしもスコアを高くすることはできないのですね...
L2正則化についても,同様に評価しました.
以下の例は,alpha=0.005, max_iter=50000 の 例です.
# alpha=0.005, max_iter=50000
R^2 score (train case) = 0.9159618987334425
R^2 score (test case) = 0.7813535143177984
こちらも過学習を抑えられていることが確認できました.
ロジスティック回帰
続いてロジスティック回帰について説明します.
ロジスティック回帰は,名前に「回帰」とついているので,これまでと同じ回帰分析を行うものと思われがちですが,実はクラス分類(数値ではなく,予め定められたラベルを予測すること)を行います.なぜ「回帰」と呼ぶのかについては,後ほど説明します.
原理
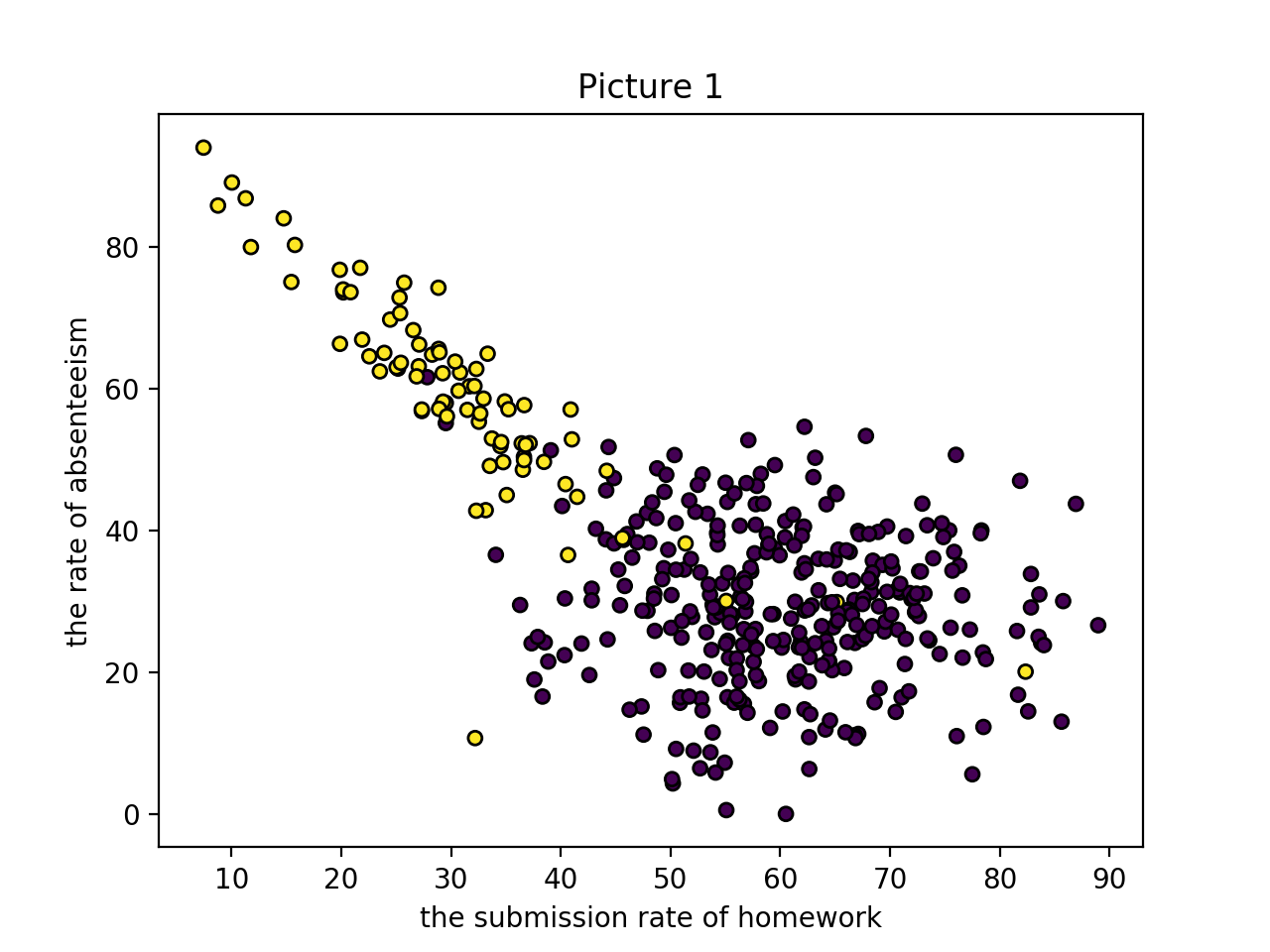
このグラフは,とある大学の授業において,学生の「単位取得状況」と「課題の提出率・授業の欠席率」の相関を表したものです(筆者が擬似的に生成したものです).グラフの横軸は課題の提出率(%),縦軸は授業の欠席率(%)を表しています.また紫色のプロット(ラベルは0とする)は単位を取得できたことを表し,黄色のプロット(ラベルは1とする)は単位を落としたことを表します.
グラフを見ると,課題の提出率が高いほど,授業の欠席率が低いほど単位を取得できていることがわかります.当たり前ですね.
ではロジスティック回帰を使って,未知データが入力されたときに,その人が単位を取得できるのか予測したいと思います.
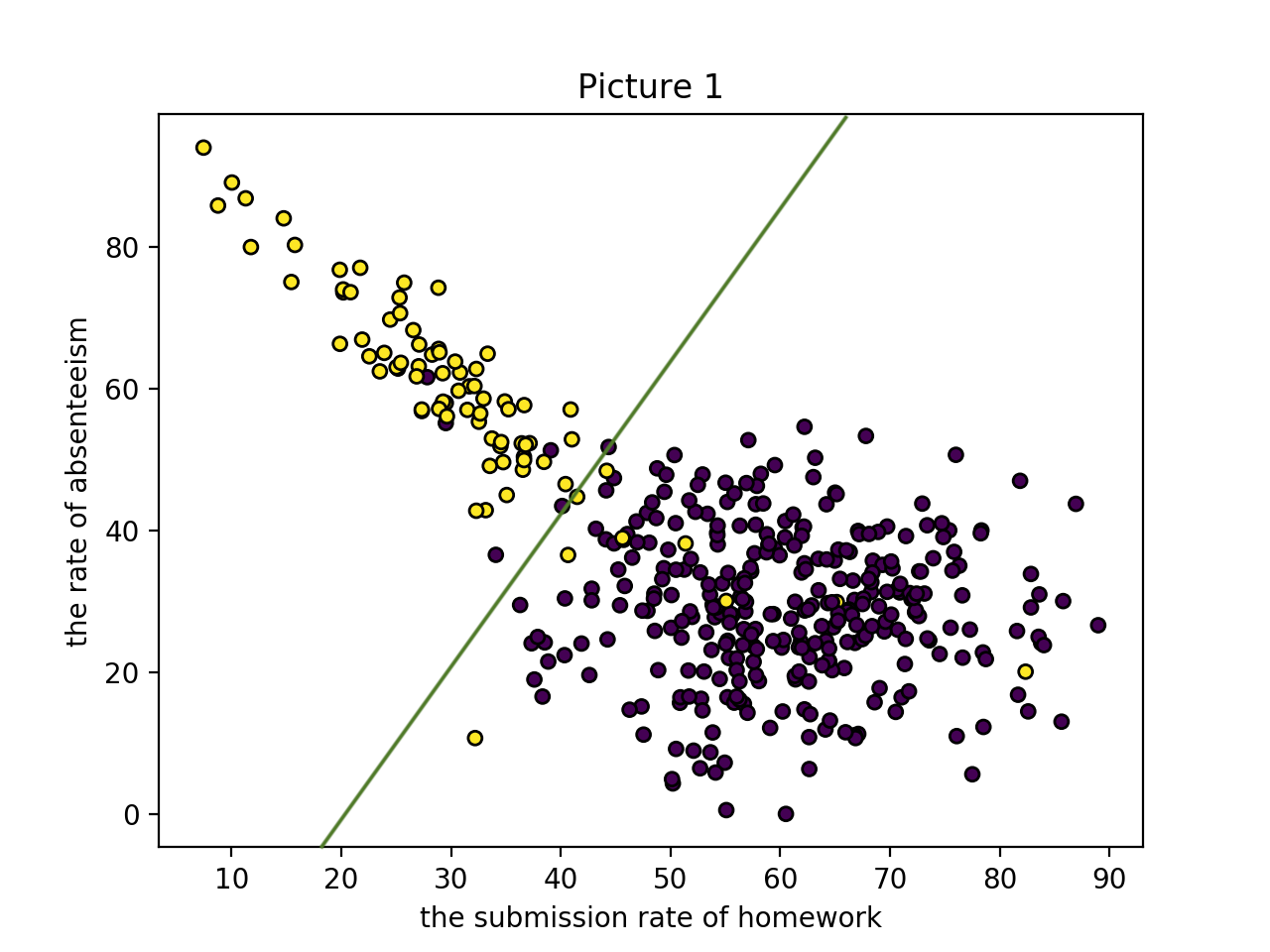
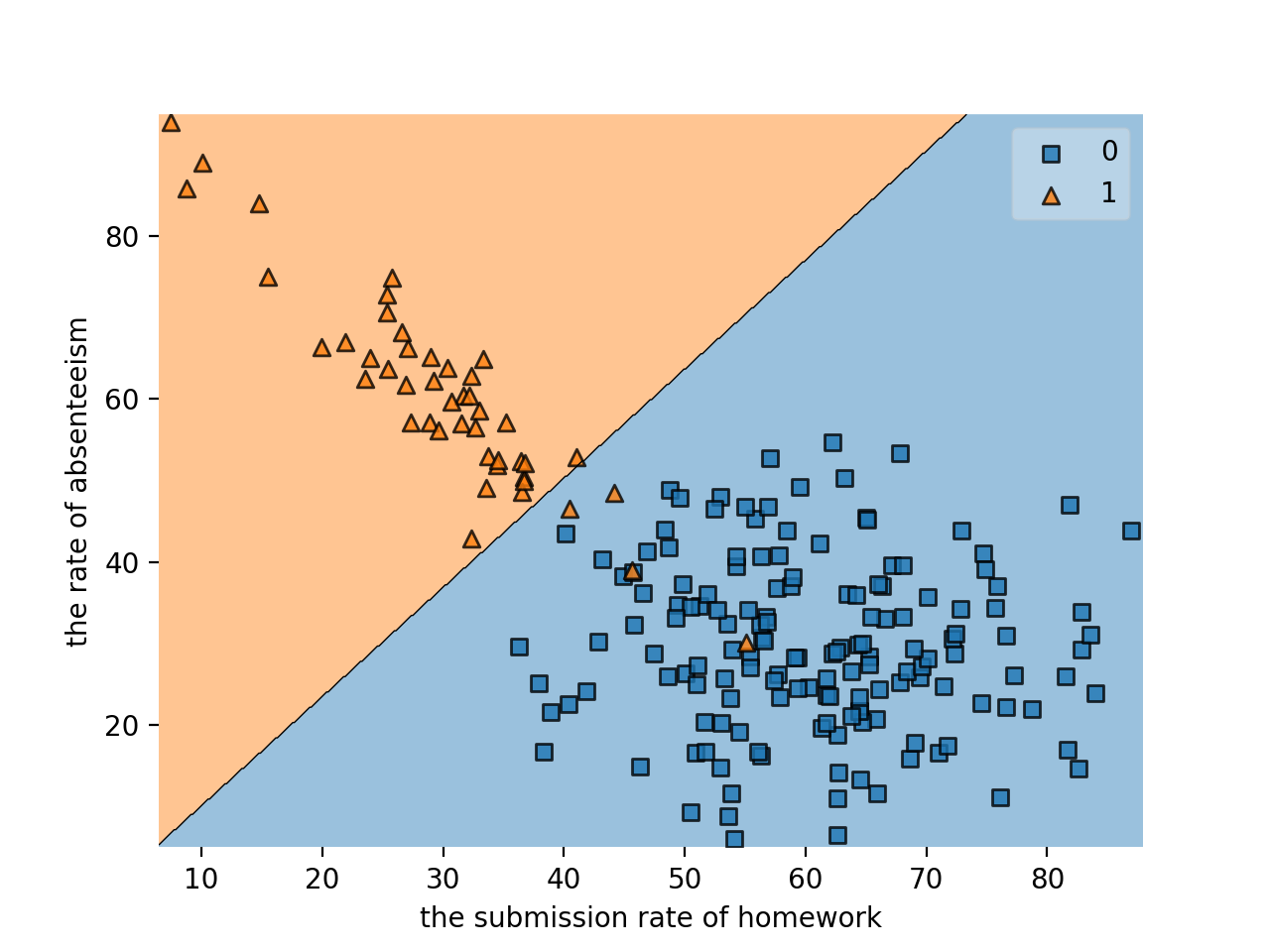
ロジスティック回帰では,以下のように,きれいに群を分割することを目標とします.
では,ロジスティック回帰の詳細について解説します.
先ほどの例(「単位取得状況」と「課題の提出率・授業の欠席率」の相関の例)を元に話を進めます.まず,以下のような線形関数を作成します.
$$z = w_0 + w_1 \times (課題の提出率) + w_2 \times (授業の欠席率)$$
いま,$w_i$は任意の実数を値をとるので,$z$も$-\infty$から$\infty$の間の値となります.
ロジスティック回帰の出力はラベルなので,出力は0から1の範囲である必要があります.
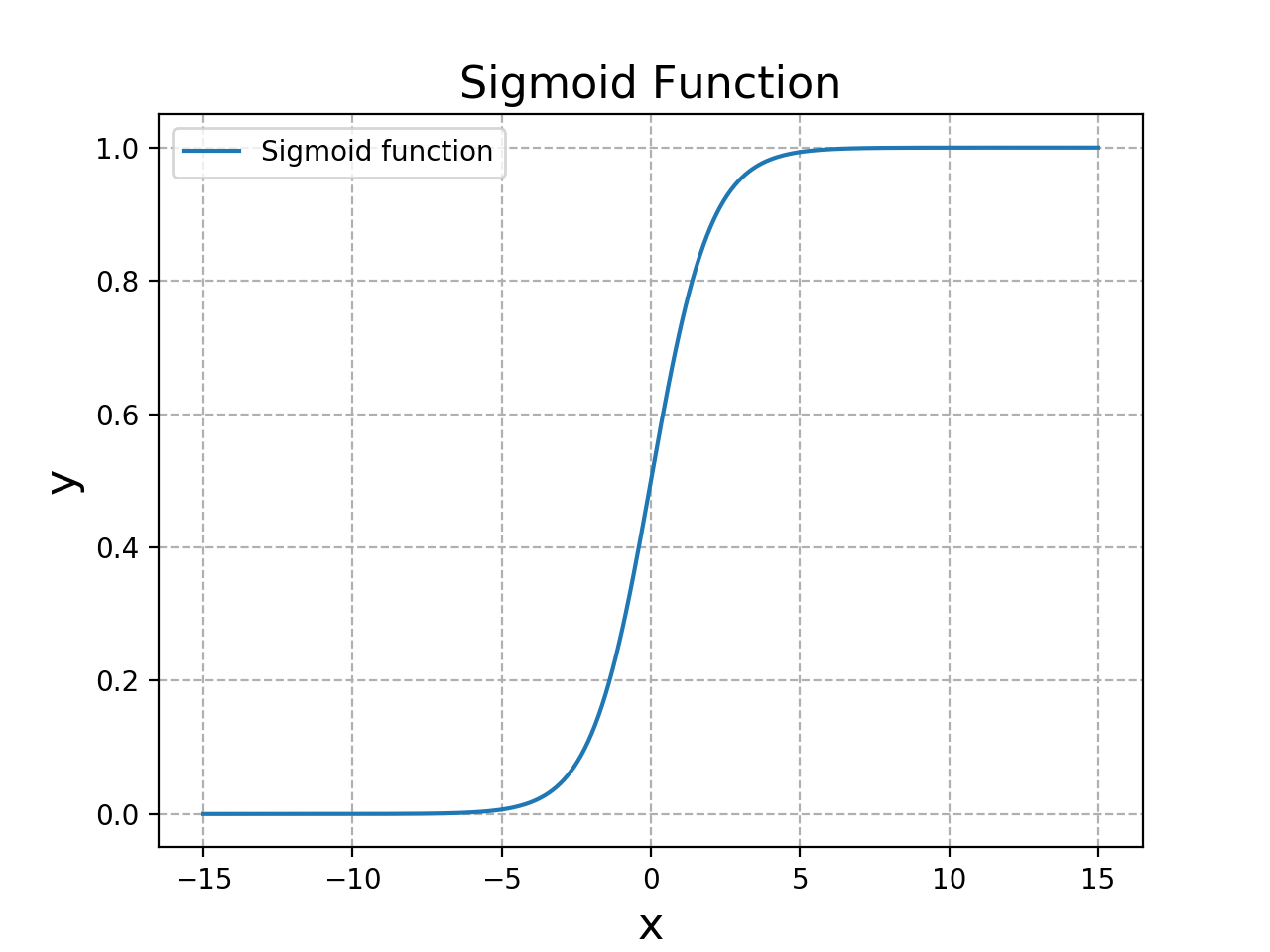
そこで,以下の「シグモイド関数$\sigma$」というものを使用します.
$$\sigma(z) = \frac{1}{1+\exp{(-z)}}$$
シグモイド関数は以下のような単調増加のグラフとなり,$z=0$のときに$\sigma(z)=0.5$となります.
$\sigma(z) > 0.5$ならばラベル1,そうでない場合はラベル0と識別します.ロジスティック回帰は,データがラベル1と分類される確率を0から1の値で回帰して,その結果からラベルを分類するアルゴリズムなので,ロジスティック「回帰」と呼ぶのです.
いま,$z = w_0 + w_1 \times (課題の提出率) + w_2 \times (授業の欠席率)$より,
$$\sigma(z) = \frac{1}{1+\exp{(-(w_0 + w_1 \times (課題の提出率) + w_2 \times (授業の欠席率)))}}$$
となります.
あとは,適切なパラメータ$w_0, w_1, w_2$を付与することによって,入力データを精度良くラベル付けすることができます.
本来であればパラメータの求め方についても説明するべきなのですが,数学的に理解が難しい内容となっており,本記事でカバーするべきでないと判断したので,説明を省略します6.
パラメータの求め方について詳しく知らなくても,scikit-learnがよしなにやってくれるので問題ないです.
実装
scikit-learnを用いてロジスティック回帰を実装します.
まず,擬似データを生成します.以下のコードを実行すると,1枚目のようなグラフを生成することができます.
from sklearn.datasets import make_classification
import matplotlib.pyplot as plt # グラフ化するために必要なライブラリ
# 課題の提出率・授業の欠席率と,単位取得状況(0: 単位取得,1: 落単)に関する
# 擬似データを作成
N_SAMPLE = 400
x_data, y_data = make_classification(random_state=8,
n_samples=N_SAMPLE,
n_features=2,
n_redundant=0,
n_informative=2,
n_clusters_per_class=1,
shift = [3, 3],
weights=[0.8, 0.2],
scale = [15, 15],
n_classes=2)
# 擬似データをグラフ化
plt.title("Picture 1")
plt.scatter(x_data[:, 0], x_data[:, 1], marker='o', c=y_data, s=25, edgecolor='black')
plt.xlabel("the submission rate of homework")
plt.ylabel("the rate of absenteeism")
plt.show()
scikit-learnに存在するmake_classificationメソッドを使用することで,簡単に分類問題用のデータを生成することができます.
続いて,ロジスティック回帰を適用します.そのために以下のコードを記述します.
やっていることは,以下の通りです.
- ロジスティック回帰に必要なライブラリをインポート
- 訓練データとテストデータに分割する
- ロジスティック回帰を適用する (
linear_model.LogisticRegressionメソッドを使用) - 学習結果から,ラベルの境界を描く
- 性能を評価する
# ロジスティック回帰に必要なライブラリをインポート
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn import linear_model # linear_model.LogisticRegression()でロジスティック回帰を実現
from mlxtend.plotting import plot_decision_regions # クラスの境界を描くためのメソッド
# 訓練データとテストデータに分割する
x_data_train, x_data_test, y_data_train, y_data_test = x_data[:N_SAMPLE//2], x_data[N_SAMPLE//2:], y_data[:N_SAMPLE//2], y_data[N_SAMPLE//2:]
# ロジスティック回帰を適用する
clf = linear_model.LogisticRegression()
clf.fit(x_data_train, y_data_train)
# 境界を描く
plot_decision_regions(x_data_test, y_data_test, clf=clf, res=0.01, legend=1)
plt.xlabel("the submission rate of homework")
plt.ylabel("the rate of absenteeism")
plt.show()
# テストデータで性能評価する
print('訓練データの精度: {0}'.format(clf.score(x_data_train, y_data_train)))
print('テストデータの精度: {0}'.format(clf.score(x_data_test, y_data_test)))
上記を実行すると,以下のようなグラフと実行結果が出力されます.
訓練データの精度: 0.955
テストデータの精度: 0.98
非常に精度よく分類できていることが分かりますね.
最後に,未知データを分類させてみます.
「課題の提出率60%, 授業の欠席率が30%」の場合と,「課題の提出率20%, 授業の欠席率が60%」の場合に,単位取得をできるか予測してみます.
# 課題の提出率60%, 授業の欠席率が30%の場合,単位取得できるか予測
credit = clf.predict([[60, 30]])
if credit == 0:
print("あなたはおそらく,単位を取得できます。")
else:
print("あなたはおそらく,単位を落とします。")
# 課題の提出率20%, 授業の欠席率が60%の場合,単位取得できるか予測
credit = clf.predict([[20, 60]])
if credit == 0:
print("あなたはおそらく,単位を取得できます。")
else:
print("あなたはおそらく,単位を落とします。")
# 課題の提出率60%, 授業の欠席率が30%の場合
あなたはおそらく,単位を取得できます。
# 課題の提出率20%, 授業の欠席率が60%の場合
あなたはおそらく,単位を落とします。
上記のような結果になりました.正しく分類できていることは,上の境界グラフからもわかりますね.
ナイーブベイズ学習
最後に,ナイーブベイズ学習について説明します.
ナイーブベイズ学習は,テキストデータの分類を得意とするアルゴリズムです.
例えば,与えられたテキストデータに,最適なカテゴリ(スポーツ,政治,音楽,エンタメ,...)をつける際にナイーブベイズ学習が利用されたりします.この状況を前提にして,話を続けます.
原理
ナイーブベイズ学習は,名前にもある通り,以下の「ベイズの定理」を土台としたアルゴリズムです.
$$ P(C|D) = \frac{P(D|C)P(C)}{P(D)}$$
ここで,$C$ はモデルのパラメータ(未知の値),$D$は既知のテキストデータとします.
左辺は,テキストデータが与えられた場合の,パラメータ$C$が発生する条件付き確率です.この条件付き確率を最大にする$C$を見つけることが目標になります.
左辺を最大にするには,右辺の分子 $P(D|C)P(C)$ を最大にすればOKです(分母は各$C$において共通なので,考慮しなくても良いです).
$P(C=c)$は,カテゴリ $c$ が発生する確率を指し,以下の式で表せます.
$$P(C= c) = \frac{訓練データにおけるカテゴリ c のテキスト数}{訓練データにおける全テキスト数} $$
$P(D|C)$は,カテゴリが分かっているときに,分類対象のテキストデータ$D$が生成される確率を表します.ここで$D$を,構成されている各単語の集合 $(w_1, w_2, ..., w_k)$ と捉えることによって,$P(D|C)$を以下のような同時確率に変換することができます.
$$P(D|C) = P(w_1, w_2, ..., w_k|C)$$
上記の同時確率を求めるのは非常に大変です.
そこで,「各単語の相関関係を無視する(つまり各単語が独立にテキストに出現する)」という仮定をおくと,同時確率を以下のように簡単に求めることができます(この仮定が**「ナイーブ」**ベイズと呼ばれる理由です).
$$P(D|C) = \prod_{i}P(w_i|C)$$
$P(w_i|C=c)$は,カテゴリが$c$と分かっているときに,単語$w_i$が出現する確率で,以下のように簡単に求められます.
$$P(w_i|C=c) = \frac{訓練データ全体でのカテゴリcに属する単語w_iの出現回数}{訓練データ全体でのカテゴリcに属する全単語の出現回数}$$
これで$P(D|C)P(C)$を計算することができます.
あとは,$C$を変化させて,$P(D|C)P(C)$を最大にする$C$を見つけることができればOKです.
実装
まず使用するデータセットを取得します.
今回は,scikit-learnに用意されているfetch_20newsgroupsデータを使用します.
まずはfetch_20newsgroupsデータの中身をみていきましょう.
from sklearn.datasets import fetch_20newsgroups # 今回使うデータセット
train = fetch_20newsgroups(subset='train') # 訓練データを読み込む
test = fetch_20newsgroups(subset='test') # テストデータを読み込む
print('=== カテゴリ一覧表示 ===')
print(train.target_names)
print("訓練データの総数 =", len(train.data))
print("テストデータの総数 =", len(test.data))
print('=== 訓練データの3つめの記事を表示する ===')
print(train.data[2])
print('=== 訓練データの3つめの記事のラベルindexとラベル名を表示する ===')
print(train.target[2], train.target_names[train.target[2]])
=== カテゴリ一覧表示 ===
['alt.atheism', 'comp.graphics', 'comp.os.ms-windows.misc', 'comp.sys.ibm.pc.hardware', 'comp.sys.mac.hardware', 'comp.windows.x', 'misc.forsale', 'rec.autos', 'rec.motorcycles', 'rec.sport.baseball', 'rec.sport.hockey', 'sci.crypt', 'sci.electronics', 'sci.med', 'sci.space', 'soc.religion.christian', 'talk.politics.guns', 'talk.politics.mideast', 'talk.politics.misc', 'talk.religion.misc']
訓練データの総数 = 11314
テストデータの総数 = 7532
=== 訓練データの3つめの記事を表示する ===
From: twillis@ec.ecn.purdue.edu (Thomas E Willis)
Subject: PB questions...
Organization: Purdue University Engineering Computer Network
Distribution: usa
Lines: 36
well folks, my mac plus finally gave up the ghost this weekend after
starting life as a 512k way back in 1985. sooo, i'm in the market for a
new machine a bit sooner than i intended to be...
i'm looking into picking up a powerbook 160 or maybe 180 and have a bunch
of questions that (hopefully) somebody can answer:
* does anybody know any dirt on when the next round of powerbook
introductions are expected? i'd heard the 185c was supposed to make an
appearence "this summer" but haven't heard anymore on it - and since i
don't have access to macleak, i was wondering if anybody out there had
more info...
* has anybody heard rumors about price drops to the powerbook line like the
ones the duo's just went through recently?
* what's the impression of the display on the 180? i could probably swing
a 180 if i got the 80Mb disk rather than the 120, but i don't really have
a feel for how much "better" the display is (yea, it looks great in the
store, but is that all "wow" or is it really that good?). could i solicit
some opinions of people who use the 160 and 180 day-to-day on if its worth
taking the disk size and money hit to get the active display? (i realize
this is a real subjective question, but i've only played around with the
machines in a computer store breifly and figured the opinions of somebody
who actually uses the machine daily might prove helpful).
* how well does hellcats perform? ;)
thanks a bunch in advance for any info - if you could email, i'll post a
summary (news reading time is at a premium with finals just around the
corner... :( )
--
Tom Willis \ twillis@ecn.purdue.edu \ Purdue Electrical Engineering
---------------------------------------------------------------------------
"Convictions are more dangerous enemies of truth than lies." - F. W.
Nietzsche
=== 訓練データの3つめの記事のラベルindexとラベル名を表示する ===
4 comp.sys.mac.hardware
実行結果を確認すると,このデータセットには18,846件(訓練データが11314件,テストデータが7532件)のニュース記事が含まれており,各記事は20種類存在するカテゴリのいずれかに割り当てられています.
また訓練データの3つめの記事は,ラベル4(comp.sys.mac.hardware)に属していることがわかりました.
続いて,テキストデータ中の単語を数値に置き換えます.
この際に使う表現方法として,「Bag-Of-words表現(BoW表現)」や「TF-IDF(Term Frequency Inverse Document Frequency)」などがあります.
今回はTF-IDFを使用します.TF-IDFは,各単語の重要度を評価する手法の1つです.
以下のように記述することで,簡単にナイーブベイズ学習のモデルを作成することができます.
from sklearn.feature_extraction.text import TfidfVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.pipeline import make_pipeline
model = make_pipeline(TfidfVectorizer(), MultinomialNB())
make_pipelineを使うことで,データの変換から学習・推定までの一連の処理を一つの推定器としてまとめることができます.
TfidfVectorizer()は,TF-IDFを評価するメソッドで,MultinomialNB()はナイーブベイズを用いて離散データの多クラス分類を行うメソッドです.
つまり,上記の処理によって,テキストデータからTF-IDFによって各単語の重要度を評価し,それを元にナイーブベイズ学習をするモデルを作成することができます.
あとは,これまでと同様に,訓練データを用いて学習させ,精度を評価します.
model.fit(train.data, train.target)
print('訓練データにおける精度 = {0}'.format(model.score(train.data, train.target)))
print('テストデータにおける精度 = {0}'.format(model.score(test.data, test.target)))
実行結果は以下の通りです.
訓練データにおける精度 = 0.9326498143892522
テストデータにおける精度 = 0.7738980350504514
少し過学習気味ではありますが,75%以上の確率で正しくカテゴリ分類できていることが分かります.
最後に
私は普段情報セキュリティ(情報理論・暗号理論)や離散数学に関する研究をしており,あまり機械学習について学ぶことが少なかったのですが,いざ学んでみると面白いですね.
本当はもう少しscikit-learnについて説明したり,SVCや決定木など他の教師あり学習や,教師なし学習について書きたかったのですが,機会を改めようと思います.
最後まで読んでいただきありがとうございました.
宣伝
この記事を読んで「面白かった」「学びがあった」と思っていただけた方、よろしければ LGTM、Twitter や Facebook、はてなブックマークにてコメントをお願いします!
また DeNA 公式 Twitter アカウント @DeNAxTech では、 Blog 記事だけでなく色々な勉強会での登壇資料も発信しています。ぜひフォローして下さい!
Follow @DeNAxTech
参考文献
[1] 清水 琢也,小川 雄太郎著,「AIエンジニアを目指す人のための機械学習入門」,2020年4月25日出版
[2] Andreas C. Muller, Sarah Guido著, 中田 秀基 翻訳「Pythonではじめる機械学習 ―scikit-learnで学ぶ特徴量エンジニアリングと機械学習の基礎 」, 2017年5月25日出版
[3] Github, shimitaku/MachineLearning-Book
[4] ロジスティック回帰
[5] 機械学習入門者向け Naive Bayes(単純ベイズ)アルゴリズムに触れてみる
[6] 機械学習ナイーブベイズ分類器のアルゴリズムを理解したのでメモ。そしてPythonで書いてみた。
[7] ナイーブベイズ:二項分布・多項分布に基づいたイベントモデル
[8] 第19回 ロジスティック回帰の学習
[9] 【回帰分析の数理】#5 ロジスティック回帰の導出
[10] シグモイド関数
[11] scikit-learnを用いたサンプルデータ生成
[12] 機械学習 〜 データセット生成 〜
[13] Scikit-learn でロジスティック回帰(確率予測編)
-
回帰とは,入力データが与えられたときに,対応する出力データを予測することです. ↩
-
参考文献[1], [2]で,このデータが使用されていたため,本記事でも採用しています. ↩
-
$E$ の式で $\frac{1}{2}$ が含まれていることに疑問を持った方もいらっしゃると思います.実際に必要なくても良いのですが,$\frac{1}{2}$を含めることによって,後々計算が楽になるので,一般的には$\frac{1}{2}$を含めることが多いです. ↩
-
(興味のある方向けに) 一般的には 「Moore – Penrose inverse」というものを用いて計算します. ↩
-
L1正則化とL2正則化の両者を組み合わせたElastic Netと呼ばれるモデルも存在します. ↩
-
詳しく理解したい場合は,参考文献[8], [9]等を見ると良いです. ↩