More than 5 years have passed since last update.

文字列アルゴリズムAdvent Calendar 2017

線形時間RePair

Last updated at 2017-12-23Posted at 2017-12-14

この記事は，「文字列アルゴリズム Advent Calendar 2017」14日目の記事です．

はじめに

文字列を圧縮する日々が続いています．
今日は，文法圧縮アルゴリズムのひとつであるRePair¹を，線形時間計算量で実現する方法を紹介したいと思います．

非常に高度な内容となった昨日に引き続き，今日もかなり難しい話を扱います．文法圧縮（とRePair）への入門が不十分だとはじき飛ばされるおそれがあるので，この分野になじみが薄いという方は，まず「文字列アルゴリズム Advent Calendar 2017」12日目の記事「文法圧縮入門」を読んでいただければと思います．
ちなみに，忙しい人のためにここで記事の要点を復習すると，

文法圧縮という文字列データの可逆圧縮の技術が存在する．
文法圧縮は，圧縮データとして「元の文字列を生成するようなサイズの小さい文脈自由文法」
を構築する圧縮方法である．
RePairは最頻出のbigramを置換していく文法圧縮アルゴリズムである．

という内容でした（すでに何を言っているのかわからないという方は，是非入門記事を読んでくださいね！）．

ところで，この記事では「線形時間RePair」という言葉を使っていますが，今回紹介するRePairを線形時間で実現する方法は，もともとRePairが提案された最初の論文¹に書かれています．つまり，RePairははじめから線形時間アルゴリズムとして提案されているので，「線形時間RePair」という名前は厳密には少しおかしいです．ですが，最頻出のbigramを置換していくというRePairの原理を最も愚直に実現する $O(n^2)$ 時間アルゴリズムに対して，という位置づけで，本記事ではあえてこの名称を用いることにしました．

記号と用語の定義

以降の説明を通して用いる記号と用語の約束をしておきたいと思います．

$t$ を入力文字列，$n$ をその長さとする．
$\epsilon$ を空文字を表す記号とする．
$x$ を配列または文字列としたとき，$x[i]$ で配列（文字列）の $i$ 番目の要素（文字）を表す．
ここで，$x$ の長さ $m$ に対し，$1 \le i \le m$ とする．
すなわち先頭は $x[1]$，最後尾は $x[m]$．
Bigramをひとつの変数に置換する操作をpairingと呼ぶ
（RePairの名前はRecursive Pairingという言葉に由来します）．
あるbigram $b$ をpairingするとき，文字列（変数列）中でいま
変数に置換しようとしている $b$ の出現を active bigram と呼ぶ
（文字列中の $b$ のすべての出現ではなく，いままさに置換しようとして注目している
出現1つだけを指していることに注意してください）．

線形時間RePair

基本戦略

RePairの愚直なアルゴリズムが $O(n^2)$ 時間必要になる原因のひとつは，1ステップのpairing操作ごとに毎回 $O(n)$ 時間費やして最頻出のbigramとその出現位置を探索するためでした．
線形時間RePairでは，このpairing操作を $O(n)$ 時間かけずに行います．そのために，はじめに（初期状態の文字列に対する）すべてのbigramとその頻度を数え上げて頻度表に保持しておき，以降は変数への置換のたびに，その頻度表を変更のあった箇所だけ更新していく，という戦略を取ります．

データ構造

はじめにデータ構造の準備をします．
線形時間RePairでは，配列 $A$，ハッシュ表 $H$，優先度つきキュー $Q$ の3つのデータ構造を利用します．以下，それぞれの詳細を説明します．

配列 A

この配列は，pairingを行っていく過程で，いま現在の文字列がどうなっているのか，という状態を保存しておく役割を持ちます．
すなわち，初期状態では，この配列は入力文字列（の終端記号を変数に置き換えたもの）が，途中の段階では，そのときの変数列が，終了状態では，RePairの操作が完了されすべてのbigramの出現頻度が1になった変数列が保持されています．

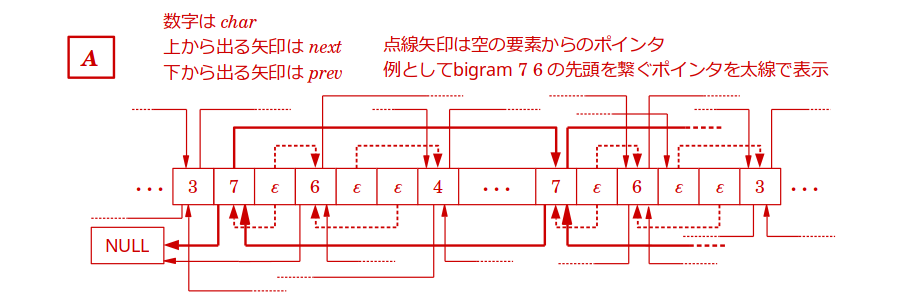
$A$ は長さ $n$ の配列で，各要素は1つの文字と2つのポインタで構成されます．説明のため，以降それぞれを $char$，$prev$，$next$ と表すことにし，$A[i]$ におけるそれらを$A[i].char$，$A[i].prev$，$A[i].next$ のように書くことにします．

ところで，pairing によってbigramが1つの変数に置き換わると，その部分を保持するのに必要な要素は2つから1つになり，不要になる要素が出てきます．そのような不要になった要素は削除せずに残しておき，空文字 $\epsilon$ に書き換えておくことで区別します．

$A$ の各要素は，$char$ に文字が入っているときといないときで別々の役割を演じます．以降では，前者を空でない要素，後者を空の要素と呼びます．それぞれにおける $char$，$prev$，$next$ の内容は以下の通りです．

空でない要素
- $A[i].char$：変数1文字．
- $A[i].prev$：$A[i]$ とその次の空でない要素の $char$ から成るbigramの，自身の1つ前の出現における先頭要素を指すポインタ．自身が先頭であるときはNULLを指す．
- $A[i].next$：$A[i]$ とその次の空でない要素の $char$ から成るbigramの，自身の1つ後ろの出現における先頭要素を指すポインタ．自身が最後の出現であるときはNULLを指す．
空の要素
- $A[i].char$：空文字 $\epsilon$．
- $A[i].prev$：$A[i]$ より前で空でない最後の要素を指すポインタ
  （$A[i+1].char$ が $\epsilon$ あるいは $i = n$ である場合は，
  このポインタは使用されない）．
- $A[i].next$：$A[i]$ より後ろで空でない最初の要素を指すポインタ
  （$A[i-1].char$ が $\epsilon$ である場合は，このポインタは使用されない）．

図示してみると次のようになります．

さて，いまある空でない要素 $A[i]$ が指定されたとき，その1つ前，あるいは1つ後ろの空でない要素へは，次のようにして定数時間でアクセスできます．

1つ前：$A[i-1].char \neq \epsilon$ ならば $A[i-1]$，
$A[i-1].char = \epsilon$ ならば $A[i-1].prev$ が指す要素．
1つ後ろ：$A[i+1].char \neq \epsilon$ ならば $A[i+1]$，
$A[i+1].char = \epsilon$ ならば $A[i+1].next$ が指す要素．

すなわち，空でない要素 $A[i]$ について，それを含むbigramは定数時間で取得できます．

以降，特に誤解がないと思われる部分では，$A$ を各要素の $char$ が並んだ文字列のように見なして説明していることがあります（たとえば，厳密には $A[i].char$ と言うべきところを，単に $A[i]$ と言っていることがある，ということです）．

ハッシュ表 H

このハッシュ表は，bigramに関する情報への索引としての役割を持ちます．
すなわち，$H$ の各要素はそれぞれdistinctなbigramで束縛されます（言い換えれば，$H$ はbigramに対してそれに紐づけられた要素を1つ返します）．

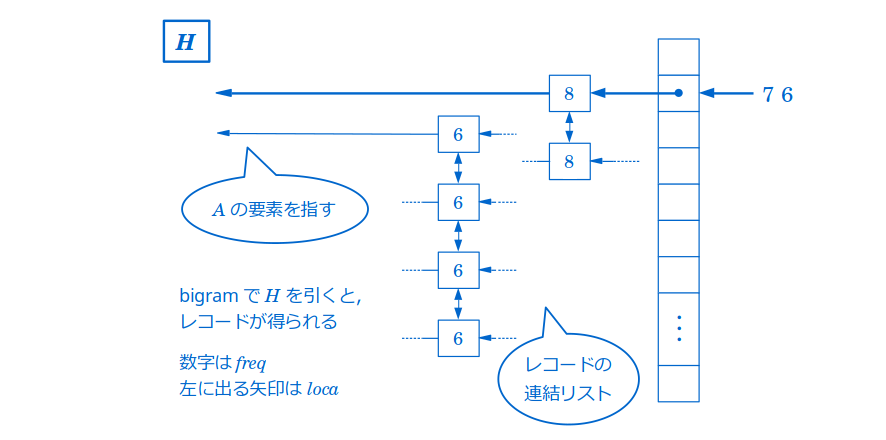
ここでは，bigram $b$ で束縛された $H$ の要素を $H(b)$ と書くことにし，これを $b$ のレコードと呼びます．各要素には1つの整数と1つのポインタがあり，ここではそれぞれを $freq$，$loca$ と表すことにします．また $A$ と同様，$H(b).freq$，$H(b).loca$ といった表記を用います．その中身は，

$H(b).freq$：$b$ の出現頻度を表す整数，
$H(b).loca$：$b$ の最初の出現における先頭の $A$ の要素を指すポインタ，

です．さらに，$freq$ が同じレコード同士をポインタで繋ぎ，それらを双方向連結リストとして持っておきます．

優先度つきキュー Q

このキューは，bigramの頻度表としての役割を持ちます．優先度の尺度にはbigramの頻度を用い，配列で実装します．
いま，初期状態の文字列において最も出現するbigramの頻度を $f_{ini}$ とすると，配列の $i$ 番目 $(1\le i \le f_{ini})$ の要素は頻度 $i$ のbigramのレコードの双方向連結リストへのポインタを保持します²．
ここで気をつけたいのが，いまここから一段階pairingしたとき，それによって新たに出現するどんなbigramも，出現頻度が $f_{ini}$ を超えるようなことはない，ということです．これはすべての段階について成り立ちます．言い換えれば，最も出現するbigramの出現頻度は，pairingしていくにつれて減少していく一方です．したがって，$f_{ini}$ 番目より後ろにさらに配列の要素が必要になるようなことはありません．

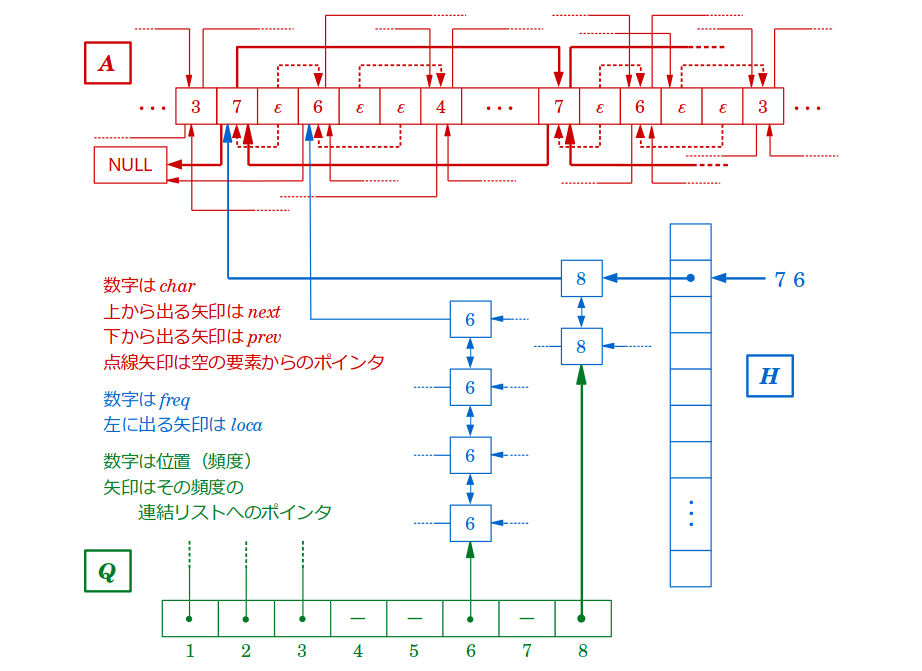
以上でようやく，データ構造の準備ができました．
$A$，$H$，$Q$ の関係を描くと下図のようになります．

アルゴリズム

いま，active bigramが $A[i]~A[j]$ であるとき（$A[i]$，$A[j]$ は互いに1つ前後の空でない要素），$A[i]$ の1つ前の空でない要素を $A[l]$，$A[j]$ の1つ後ろの空でない要素を $A[r]$ とします．

さて，いよいよRePairが線形時間になります．以下は上記のデータ構造を駆使したアルゴリズムの全体像です．
必要以上に説明が煩雑になるため，$A[l]$ や $A[r]$ が存在しない場合（つまり，$i=0$ や $j=n$ のような場合）について明記していない部分がありますが，単にそこの処理を行わなかったり，ポインタの指す要素がNULLになったりするだけで，別段特別な手順は不要です．
箇条書き文章のうち，数字を冠したものはアルゴリズムの手順，▪を冠したものは手順の説明になっています．

【前処理】
1. 入力文字列 $t$ を変数列に置換，その各変換を規則に追加する．
2. 得られた変数列に対し，$A$，$H$，$Q$ を構築する．
【最頻出bigramの取得】
1. $Q$ の頻度2以上の部分が空なら 4.【最後の規則の追加】へ，そうでないなら，このまま以下を実行する．
2. $Q$ からpop（dequeue）する．得られたレコードを $rec$ とする．$rec.loca$ の指す要素とその次の空でない要素から成るbigramを $b$ とする．
  - Popには $Q$ の最後尾のポインタを辿り，行く先の連結リストの先頭の要素を取り出します．
  - $rec$ は $b$ のレコードであり，$b$ はいま最も出現頻度の多いbigramのひとつです．
3. $H$ から $b$ の束縛を削除する³．
4. 新たな変数 $x$ を用意し，$x \rightarrow b$ を規則に追加する．
【Pairingとそれに伴うデータ構造の更新】
1. $A$ における $b$ の最初の出現を取得する．
  - $rec.loca$ からみつけられます．いまこれが active bigram の先頭 $A[i]$ です．
2. 出現頻度が減るbigramのレコードを更新する．
  - $A[l]A[i]$ および $A[j]A[r]$ は，active bigram $A[i]A[j]$ が置換されることで出現頻度が減少します．
  - $H(A[l]A[i]).freq$ の値をデクリメントし，$Q$ のひとつ下の頻度のポインタが指す連結リストにレコードを繋ぎ直します．$H(A[l]A[i]).freq < 1$ となったら，レコードは削除します⁴．$H(A[j]A[r])$ についても同様に行います．
  - さらに，$A[l].prev$ の指す要素の $next$ が $A[l].next$ の指す要素を指すように，$A[l].next$ の指す要素の $prev$ が $A[l].prev$ の指す要素を指すように変更します．$A[j]$ についても同様に行います．
3. Active bigram を変数に置換する．
  - $A[i].char$ を $x$ に，$A[j].char$ を $\epsilon$ に書き換えます．加えて，$A[j].next$ の指す要素を $A[r]$ に，$A[r-1].prev$ の指す要素を $A[i]$ に変更します．
4. $A[i].next \neq$ NULL ならば，そのポインタの指す要素を新たな $A[i]$（すなわちactive bigramの先頭）とし，3.2.へ戻る．$A[i].next \neq$ NULL ならば，以下の手順へ移行する．
  - $A[i].next$ を辿ることで，置換すべき次の $b$ の出現に定数時間で移動できます．ポインタがNULLを指している場合，いまいる場所が $b$ の最後の出現ということになります．このとき，現在の $A[i]$ を指すポインタ $last$ を保持しておきます．
  - ここまでは，先頭の出現から順方向にデータ構造の更新をしてきましたが，以降は逆方向にデータ構造を更新していきます．
5. 新たなbigram $A[l]A[i]$ のレコードを登録・更新する．
  - $H(A[l]A[i])$ がすでに存在する場合
    - まず，$H(A[l]A[i]).freq$ をインクリメントし，$Q$ のひとつ上の頻度のポインタが指す連結リストにレコードを繋ぎ直します．
    - $A[l].next$ を $H(A[l]A[i]).loca$ の指す要素を指すように，$H(A[l]A[i]).loca$ の指す要素の $prev$ を $A[l]$ を指すように変更します．これで，bigram $A[l]A[i]$ の次の出現との双方向連結が実現しました．
    - 最後に，$H(A[l]A[i]).loca$ を現在のactive bigramの先頭である $A[l]$ に設定し，$A[l].prev$ がNULLを指すように変更します．
  - $H(A[l]A[i])$ が存在しない場合
    - $H(A[l]A[i])$ を作成し，$Q$ の頻度1のポインタの指す連結リストに繋ぎます．また，$H(A[l]A[i]).loca$ を現在のactive bigramの先頭である $A[l]$ に設定し，$A[l].prev$ がNULLを指すように変更します．
6. 新たなbigram $A[i]A[r]$ のレコードを登録・更新する．
  - $H(A[i]A[r])$ がすでに存在する場合
    - まず，$H(A[i]A[r]).freq$ をインクリメントし，$Q$ のひとつ上の頻度のポインタが指す連結リストにレコードを繋ぎ直します．
    - 次に，$A[i].next$ の指す要素の $prev$ がNULLを指すように設定します．その後，$A[i].next$ を $H(A[i]A[r]).loca$ の指す要素を指すように，$H(A[i]A[r]).loca$ の指す要素の $prev$ を $A[i]$ を指すように変更します．これで，bigram $A[i]A[r]$ の次の出現との双方向連結が実現しました．
    - 最後に，$H(A[i]A[r]).loca$ を現在のactive bigramの先頭である $A[i]$ に設定します．
  - $H(A[i]A[r])$ が存在しない場合
    - $H(A[i]A[r])$ を作成し，$Q$ の頻度1のポインタの指す連結リストに繋ぎます．また，$H(A[i]A[r]).loca$ を現在のactive bigramの先頭である $A[i]$ に設定します．
7. $A[i].prev \neq$ NULL ならば，そのポインタの指す要素を新たな $A[i]$ とし，3.5.へ戻る．$A[i].prev =$ NULL ならば，以下の手順へ移行する．
  - $A[i].prev =$ NULL のときは，すべての新たな $x$ と次の文字から成るbigramについて，更新が完了したことになります．
8. 2.【最頻出bigramの取得】に戻る．
【最後の規則の追加】
1. $A$ の要素を先頭から順に見て，$\epsilon$ でない $char$ を連結した文字列 $t_{end}$ を作成する．開始記号から $t_{end}$ への変換を規則に追加し，終了する．
  - すべてのbigramの出現頻度が1である文字列を右辺とする規則を追加し，終了です．

計算量解析

最後に，上記のアルゴリズムが本当に線形時間計算量を達成できているのか確認したいと思います．

まず，1.【前処理】および 4.【最後の規則の追加】はともに $O(n)$ 時間で可能です．2.【最頻出bigramの取得】も，$Q$ に指されている連結リストの要素数は $O(n)$ 個なので，$O(n)$ 時間で済みます．

問題は 3.【Pairingとそれに伴うデータ構造の更新】です．緻密に張り巡らされたポインタにより，ここでの各操作はすべて定数時間で行えるので，ループがどれだけ発生するかが焦点になります．
いま，置換しようとしているbigram $b$ の出現回数を $m$ とすると，3.2.から3.4.にかけてのループは $m$ 回，3.5.から3.7.にかけてのループは $m$ 回となります．したがって，1ステップのpairingとそれに伴うデータ構造の更新は $O(m)$ 時間で行われます．

ここで注意したいのが，1ステップのpairingによって，$A$ の空でない要素の数（すなわち文字列の長さ）は $m$ 減少するということです．ゆえに，$A$ の要素にこれから置き換えるbigramの先頭として訪問可能な回数は，すべてのステップを合わせて高々 $n$ 回となります（すべてのステップの $m$ を足し合わせると $n$ 以下である，ということです）．よってこの部分も $O(n)$ 時間で実行可能です．

以上より，めでたく上記のアルゴリズムが線形時間計算量であることが確認できました．

ところで，ここまで空間計算量についてはまったく言及してきませんでしたが，このアルゴリズムは $O(n)$ word spaceになっています．しかしながら（注釈にも添えましたが），上記では節約できる余計な空間を，説明のために残してある部分がいくつかあります．こうした箇所を削ると，RePairは $O(n)$ time，$5n+4k^2+4k'+\lceil \sqrt{n+1} \rceil - 1$ word space（$k$ は入力文字列 $t$ 中の文字の種類数，$k'$ は構築した文脈自由文法の変数集合と終端記号集合の要素数の和）の計算量を達成できます．

おわりに

今日はRePairを線形時間計算量で実現する方法を紹介しました．
この記事の要点は以下の通りです．

RePairは線形時間計算量で実現できる．

お疲れさまでした．
誤字・脱字，内容の間違いなどありましたらご指摘いただけると幸いです．

N.Jesper Larsson and Alistair Moffat, "Off-line dictionary-based compression", Proceedings of the IEEE, 88(11):1722-1732, 2000. ↩ ↩²
実際には，出現頻度が1であるようなbigramのレコードは保持しません．そのため，$Q$ の先頭は頻度2のbigramのレコードの連結リストへのポインタを指し，$i$ 番目の要素には頻度 $i+1$ のものへのポインタが格納されることになります．新しく出現したbigramのレコードを保持するか否か（それが頻度2以上になるのか否か）の判定についてはこの記事には書ききれませんでしたが，多少の工夫で実現することができます．また，実際には $Q$ の配列のサイズは $f_{ini}$ より小さい値を取ります．この部分についてもやはりこの記事には書ききれませんでしたが，こうした工夫により作業領域を減らすことができます． ↩
実際には，これは行いません．というのも，たとえば ${\rm aaa}$ のように同じbigramがオーバーラップしている部分を置換するときに，bigram $b$ のレコードへの束縛が必要になるためです．この記事では説明していませんが，こうしたオーバーラップ部分にもちょっとした工夫で対処できます． ↩
ここでは全体を通しての整合性の観点から頻度1のbigramのレコードも保持していますが，実際には不要なので，$freq$ が1以下になった時点でそのレコードは削除して構いません． ↩

You get articles that match your needs
You can efficiently read back useful information
You can use dark theme

What you can do with signing up